基于SKPCA 的卫星整流罩空调系统传感器故障检测研究

汪 辉，税爱社，宗福兴，陈 帆

(后勤工程学院 后勤信息与军事物流工程系，重庆401311)

0 引 言

传感器作为空调系统的“电五官”，其运行状态关系到监控参数的稳定性和准确性。为及时发现传感器故障，目前广泛采用主元分析(principal component analysis，PCA)［1，2］、独立成分分析(independent component analysis，ICA)［3，4］、偏 最 小 二 乘(partial least squares，PLS)［5，6］及Fisher 判别分析(fisher discriminant analysis，FDA)［7，8］等方法，由于这些方法的系统线性和历史数据高斯分布的假设，在空调系统传感器故障检测应用中常常存在误报和漏报的问题，不能满足作为调节卫星发射环境温湿度的整流罩空调系统对传感器故障检测的高可靠性要求。统计量核主元分析(statistics kernel principal component analysis，SKPCA)方法将统计量模式分析(statistics pattern analysis，SPA)方法与核主元分析(kernel principal component analysis，KPCA)方法相结合，经过两次空间变更有效地解决了信息利用率和非线性问题，可提高故障检测的可靠性。

本文在分析整流罩空调系统传感器故障模式的基础上，运用SKPCA 方法，建立整流罩空调系统传感器故障检测模型，并进行验证实验和结果分析。

1 传感器故障分析

1.1 传感器类型

卫星整流罩空调系统为全新风直流式空调，由新风预处理子系统、空调后处理子系统、制冷子系统组成。空调系统设备有风机、风阀、水泵、表冷器、电加热器、电加湿器等。统计卫星整流罩空调监控系统采集的传感器测点共有66 个，如，除湿机、表冷器等设备的温湿度测点和风阀、水阀的开度测点等。这些传感器输出的大多是温度、湿度、压力、风量以及阀门开度等连续信号，所以，传感器类型主要是属于模拟量传感器。

1.2 传感器故障模型

为了研究需要，人们已经提出了模拟量传感器故障的多种分类方法［9］。一般情况下，测量值x 的表现形式为

式中 x'为真实值，f 为系统误差，vx为随机误差。

文献［10］中按故障缘由将传感器故障分为偏置故障、漂移故障、精度下降、完全故障。其中完全故障属于硬故障，很容易辨认。偏置故障、漂移故障和精度下降属于软故障，其偏离真实值较小不易辨识出来，是重点研究对象，目前，卫星整流罩空调系统中一般出现的故障是偏置故障和精度下降故障［11］。

1)偏置故障

偏置故障就是指测量值与真实值之间相差一个恒定的常数［10］，即x=x'+C+vx，故障形式如图1(a)所示。

2)精度下降故障

精度下降故障指的是测量的均值不变，方差发生改变［10］，即f ～N(0，σ2)，σ2表示测量方差的变化，故障形式如图1(b)所示。

图1 整流罩空调系统典型的传感器故障模式Fig 1 Typical fault modes of sensor in air conditioning system of satellite fairing

如果传感器发生了偏置故障，实际偏差将越来越大，而故障传感器的值为相对平稳参量，因此，空调系统进入另外一种“准正常”的平稳运行状态;如果传感器发生了精度下降故障，故障传感器的值就会围绕真实值上下波动，这种波动运行状态为非平稳运行状态，容易引起整个系统的振荡，对系统造成更大的影响。这两类故障都属于微小故障，一旦发生故障，空调管理操作人员往往不能及时发现，给空调系统的正常运行带来了非常大的威胁。

2 空调系统故障检测SKPCA 模型建立

现在面对过程中的非线性问题，最常用的就是基于KPCA 方法。SKPCA 方法相较于KPCA 和SPA 方法的最大的不同点在于它经过两次空间变更，两次空间变更如图2所示。

第一次空间变更是构造统计量样本空间，将原始数据空间的高阶统计量信息包含进去，方便进一步分析过程数据的真实特性;第二次空间变更是将统计量样本空间映射到高维特征空间，便于解决数据间的非线性问题。

假设输入数据X∈Rn×m，n 代表样本个数，m 代表变量数目。滑动窗口宽度为l，那么，该窗口内所包含的数据Xk为

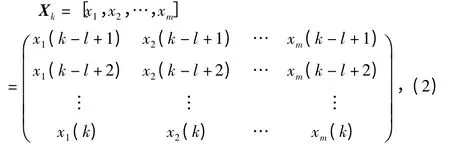
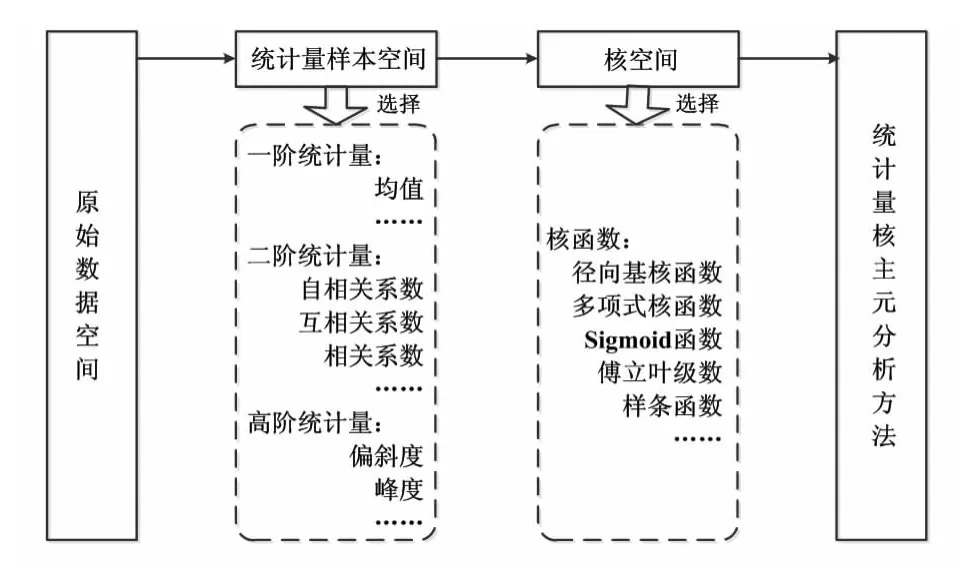
图2 SKPCA 两个空间变更Fig 2 Two space conversions of SKPCA

式中 k 当前时刻的样本编号，然后利用移动窗口技术去确定各阶次的统计量。一般统计量样本包括三个部分的统计量，即

式中 μ 为一阶统计量，即变量的均值;∑为二阶统计量，包括变量间的方差、相关系数、自相关系数和互相关系数;Ψ 为高阶统计量，包括偏斜度、峰度等。

基于SKPCA 的整流罩空调系统传感器故障检测模型可以从离线建模和在线检测两个阶段去建立，具体的步骤如下:

2.1 离线建模阶段实现两次空间变更和确定控制限

1)构建统计量模式空间

整流罩空调系统中分布的各类传感器数目比较多，所以，得到的原始数据空间的变量就比较多。文献［12］指出均值和方差在表征数据特性中非常重要，应当选取;偏斜度能够有效概括数据概率密度函数的不对称性，峰度描述的是数据概率密度函数的非高斯型，并能够在一定程度上抑制高斯噪声，应当选取;相关系数主要反映样本间时序关系，应舍去。所以，一个窗口中的数据矩阵Xk对应的统计量矩阵Sk为

式中 μk为时刻的样本均值;vk为k 时刻的样本方差;γk为k 时刻的样本变量间的偏斜度;κk为k 时刻的样本变量间的峰度。最后通过滑动窗口技术，数据集Xk每次更新一个样本，这样随着窗口的推移，得到原始数据矩阵X∈Rn×m所对应的统计量样本矩阵S∈R(n－l+1)×4m。

2)建立高维核空间

从参数优化的角度来讲，希望核函数的参数越少越好，因为参数的个数影响模型选择的复杂性;从机器学习的角度来讲，希望核函数的映射性能越强越好，因为映射性能影响故障诊断的正确性［13］。对于整流罩空调系统来说，高斯核函数比其他核函数的计算复杂性和映射性能都好，所以，应用最为广泛，其表达式为

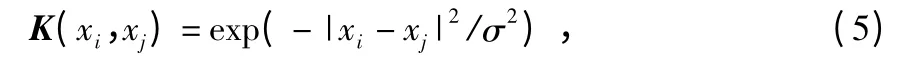
3)确定控制限

得到核矩阵以后就根据核PCA 的步骤，得到相应的T2和SPE 统计量的控制限。首先对核矩阵作中心化处理，然后得到p 个主成分所对应的特征向量的载荷矩阵P∈R(n－l+1)×p，最后得到T2和SPE 统计量以及对应的控制限［14］。

2.2 在线检测确定传感器是不是发生故障

实时采集传感器反馈的数据，对于第一个采集数据，用l－1 个正常数据补齐窗口，然后对该窗口数据进行统计量计算，根据滑动窗口技术，按照每次更新一个样本的速度，就可以得到相应的统计量样本矩阵。在高维核空间中计算统计量样本矩阵的T2和SPE 统计量，再将它们与对应的控制限作对比，用来判断当前时刻传感器是否发生故障。

根据以上描述，基于SKPCA 的整流罩空调系统传感器故障检测模型如图3 所示。

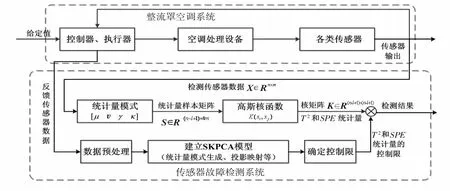
图3 基于SKPCA 的整流罩空调系统传感器故障检测模型Fig 3 Fault detection model for air conditioning system of satellite fairing based on SKPCA

3 验证实验与结果分析

3.1 表冷器控制单元

卫星整流罩空调系统被划分为若干联系密切的控制单元，各控制单元间相关性最大。因此，本文的实验以表冷器控制单元为对象来说明SKPCA 方法在整个空调系统中的有效性，表冷器控制单元单元结构如图4 所示。

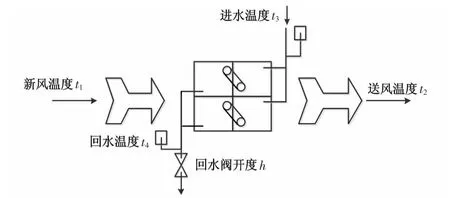
图4 表冷器结构Fig 4 Structure of surface cooler

3.2 验证实验

分别采集表冷器控制单元正常运行下t1，t2，t3，t4以及h 的数据，每隔30 s 采集一次，共采集各传感器正常数据225 组，部分数据如图5 所示。

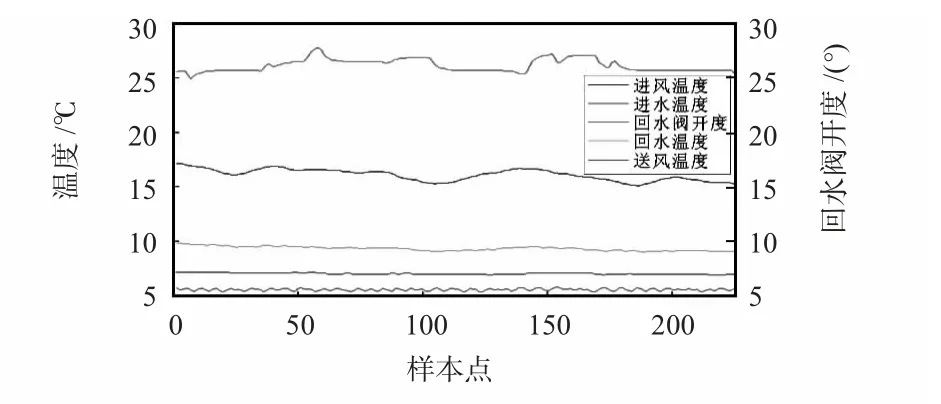
图5 5 只传感器的正常数据Fig 5 Normal datas of five sensors

仿真整流罩空调系统中模拟容易发生的偏置故障，即在进风温度200 ～225 组样本上加入一个幅值为C 的常量信号，然后将其作为测试数据，取滑动窗口宽度，利用KPCA，SPA 和SKPCA 方法分别对其进行故障检测。取不同的偏置量C，其检测结果如图6 ～图8 所示。

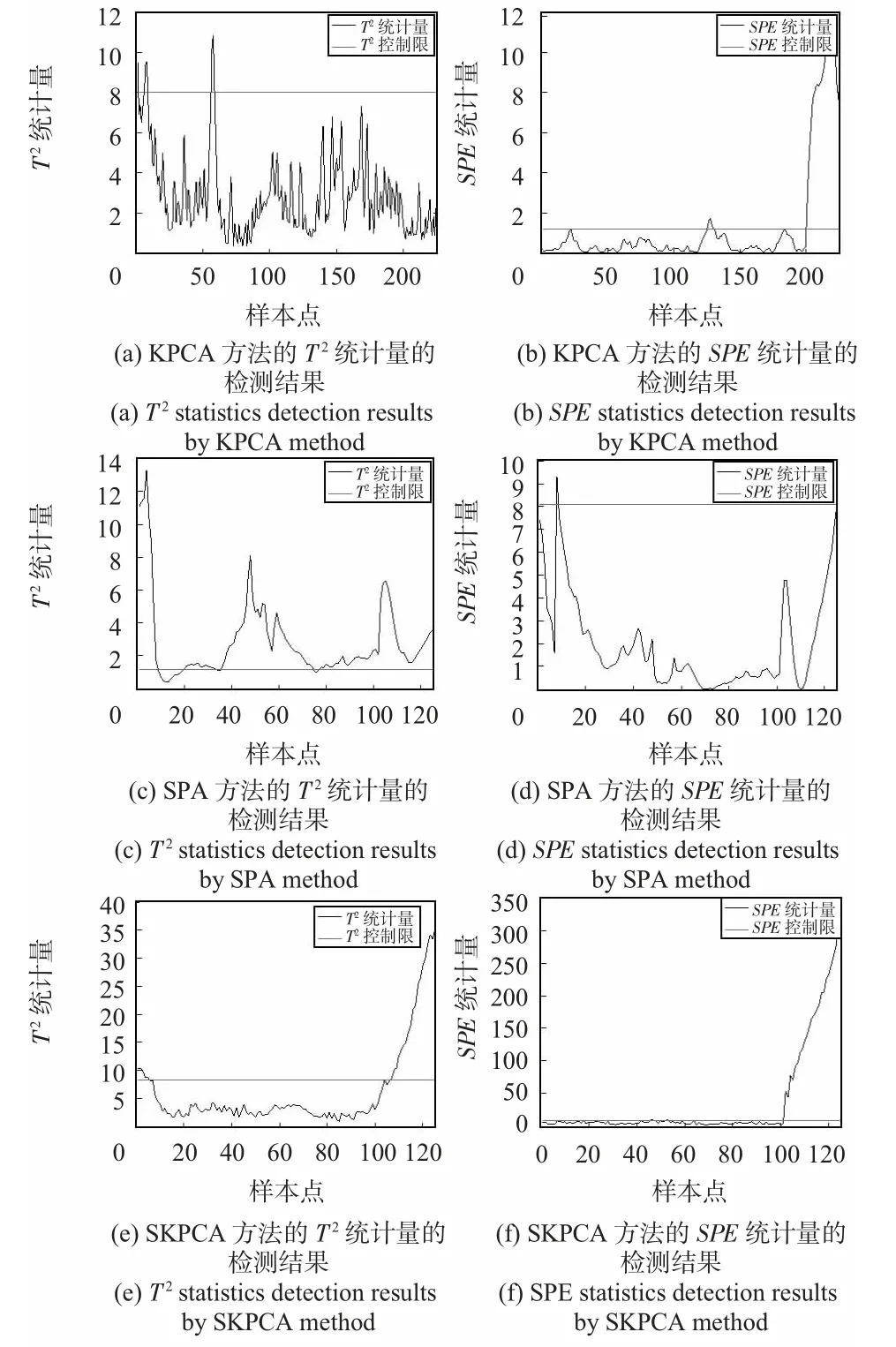
图6 C=0.15 ℃时KPCA，SPA 和SKPCA 方法的故障检测结果Fig 6 Fault detection results by KPCA，SPA and SKPCA method when C=0.15 ℃

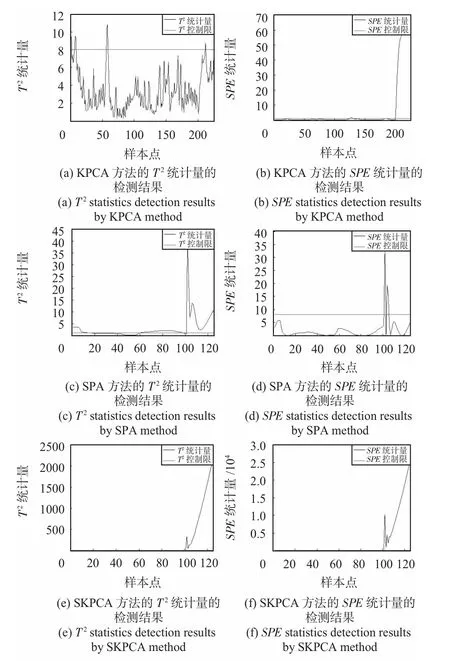
图7 C=0.70 ℃时KPCA，SPA 和SKPCA 方法的故障检测结果Fig 7 Fault detection results of KPCA，SPA and SKPCA method when C=0.70 ℃

3.3 结果分析

通过KPCA，SPA 和SKPCA 三种方法的对比实验，得到三种方法的误报率和漏报率如表1 和表2 所示。

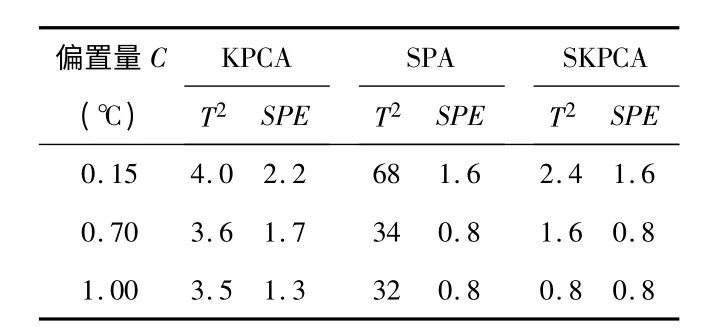
表1 三种方法的故障误报率(%)Tab 1 False alarm rates of three methods(%)

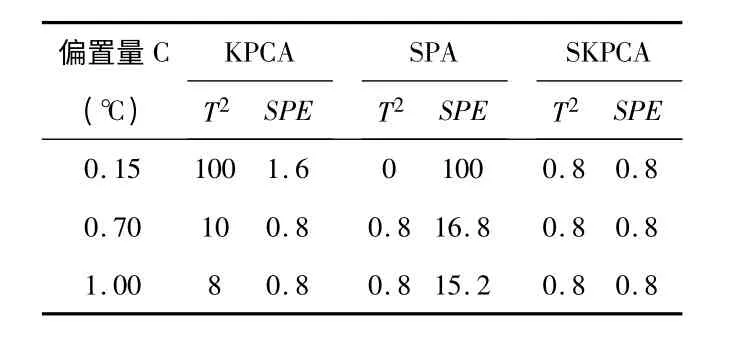
表2 三种方法的故障漏报率(%)Tab 2 False alarm rate of fault of three methods(%)

分析实验结果可以得到结论如下:

1)快速性

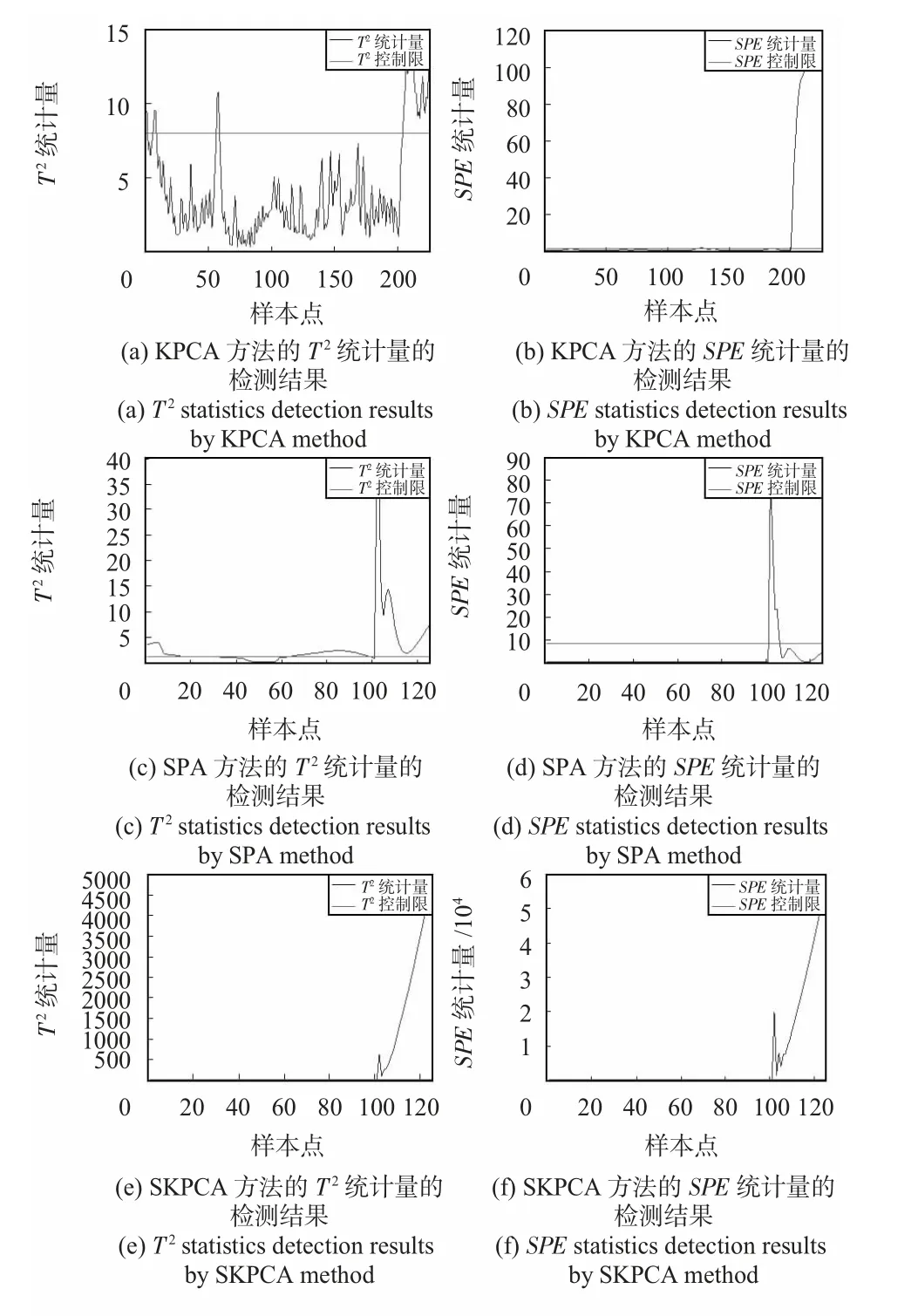
图8 C=1.00 ℃时KPCA，SPA 和SKPCA 方法的故障检测结果Fig 8 Fault detection results of KPCA，SPA and SKPCA when C=1.00 ℃

在偏置故障偏移0.15℃时，KPCA，SPA 方法无法有效检测出空调系统的偏置故障，只有SKPCA 方法可以检测出来;在偏置故障偏移0.70 ℃和1.00 ℃时SPA 和SKPCA 方法都能检测出偏置故障，但是SKPCA 方法能够更早检测出偏置故障的发生。

2)准确性

由表1 和表2 可以看出:SKPCA 方法与KPCA 和SPA方法相比，它的误报率和漏报率能够被接受，特别是SKPCA 方法对这三种偏置量的故障都有一个良好的检测效果。

4 结束语

本文将SKPCA 方法应用到整流罩空调系统传感器故障检测中，建立空调系统故障检测的SKPCA 模型，将SPA的信息提取充分的特点与KPCA 的非线性处理能力强的特点相结合，达到更好的检测效果。针对于整流罩空调系统表冷器控制单元传感器容易出现的偏置故障，进行KPCA，SPA 和SKPCA 三种方法的对比实验，实验结果表明:SKPCA 在整流罩空调系统传感器故障检测方面比其他两种方法更加快速准确，证明了该方法在整流罩空调系统传感器故障检测中的有效性。

［1］ Wold S，Esbensen K，Geladi P.Principal component analysis［J］.Chemometrics and Intelligent Laboratory Systems，1987，2(1－3):37－52.

［2］ Kruger U，Kumar S，Littler T.Improved principal component monitoring using the local approach［J］.Automatica，2007，43(9):1532－1542.

［3］ Lee J M，Qin S J，Lee I B.Fault detection of non－linear processes using kernel independent component analysis［J］.Canadian Journal of Chemical Engineering，2007，85(4):526－536.

［4］ Hyvarinen A，Oja E.Independent component analysis:Algorithms and applications［J］.Neural Networks，2000，13(4/5):411－430.

［5］ Kruger U，Zhou Y，Wang X，et al.Robust partial least squares regression:Part I，algorithmic developments［J］.Journal of Chemometrics，2008，22(1/2):1－13.

［6］ Hu Y，Ma H，Shi H.On－line batch process monitoring using multiway kernel partial［J］.Journal of DongHua University:English Edition，2011，28(6):585－590.

［7］ He Q P，Qin S J，Wang J.A new fault diagnosis method using fault directions in fisher discriminant analysis［J］.AIChE Journal，2005，51(2):555－571.

［8］ Zhu Z B，Song Z H.Fault diagnosis based on imbalance modified kernel fisher discriminant analysis［J］.Chemical Engineering Research and Design，2010，88(8):936－951.

［9］ 何富君，刘小磊，卢晓昭，等.传感器的故障诊断技术研究［J］.科学工程与技术，2010，10(26):6481－6487.

［10］艺小文.VAV 系统传感器的故障诊断研究［D］.长沙:湖南大学，2004.

［11］杜志敏.空调系统传感器多故障检测与诊断研究［D］.上海:上海交通大学，2007.

［12］Wang J，He Q P.Multivariate statistical process monitoring based on statistics pattern analysis［J］.Industrial＆Engineering Chemistry Research，2010，49(17):7858－7869.

［13］杨大炼.基于改进BFA 的旋转机械故障诊断核参数优选研究［D］.长沙:湖南科技大学，2011.

［14］杨亚伟.基于KPCA 法的定风量空调系统传感器故障诊断［D］.天津:天津大学，2010