大规模带状无线传感器网络节点定位算法*

鲁银芝，仲元昌，杨 柳，李发传

(重庆大学 通信工程学院，重庆400044)

0 引 言

长江三峡工程是举世瞩目的特大型水利工程，在其带来巨大经济、社会效益的同时，库区面临着严峻生态环境安全问题［1～3］，迫切需要建立高效的库区水环境实时监测系统，以实现水质状况监测和水域突发事件应急处理［4］。现有监测设备和方法已不能满足现实需求，必须要加强环境监测能力并提高监测水平［5，6］。无线传感器网络(WSNs)适用于环境恶劣、人类不便到达和需要长期监测的广阔区域［5～7］。在三峡库区水环境监测系统中引入无线传感器网络，能够克服传统监测方式的限制多、反应慢、无法实时连续监测等缺点［6］。

节点定位是无线传感器网络支撑技术之一，水环境监测过程中，采集的数据须包含位置信息，以便分析具体地理区域下水环境信息和处理突发性应急事件，降低风险［1～3］。因项目需要，在已有定位算法的基础上，结合应用网络特点［4，5］，本文提出了一种大规模带状无线传感器网络节点定位算法。

1 大规模带状无线传感器网络特性

三峡库区是在长江三峡这个特殊的区域，如图1，库区呈现蜿蜒的树状结构，具有明显的带状特征，且分布范围广［2］。面向三峡库区水环境监测的大规模无线传感器网络应根据其特性部署、组网。宏观上，这是一种超大规模复杂无线带状网;微观上，可将其分解成多个小型带状子网［5］。带状分布传感器网络具有自身特性［4～6］，节点定位过程中应深入分析其特点，采用合适定位算法才能取得良好效果。

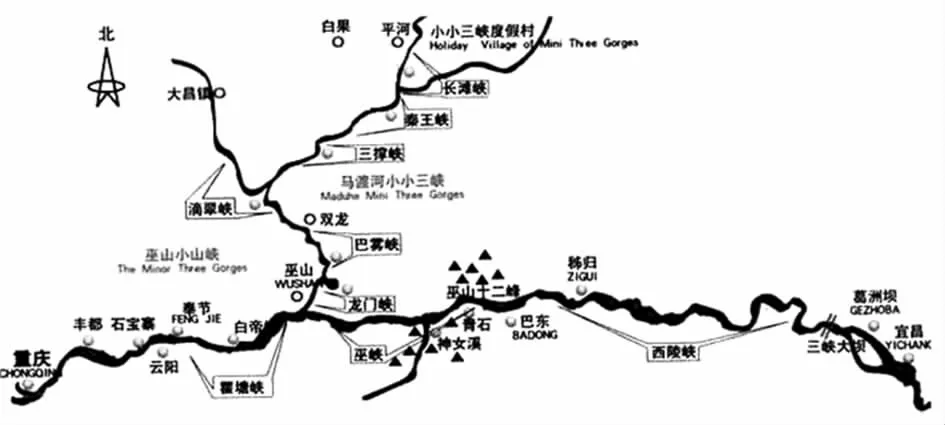
图1 三峡库区水域分布图Fig 1 Distribution of the Three Gorges Reservoir

博弈论作为数学建模分析工具已被广泛采用［7］，但很少有学者将节点定位问题与博弈论建模结合分析［8］。本文结合三峡库区水环境监测的传感器网络特性，着重将博弈论用于未知节点的定位并进行模型搭建，寻找合适方法对模型求解，改善定位算法性能。

2 无线传感器网络节点定位模型

2.1 博弈论介绍

博弈论作为研究决策主体之间行为发生直接相互作用时的建模和决策均衡问题的手段，早在十几年前已被提出［7］。近年来，博弈论思想逐渐用于无线传感器网络的研究领域，为诸如路由、拓扑控制及资源分配［8］等关键技术带来新思路。

现代博弈论可分为合作博弈和非合作博弈。合作博弈是研究人们达成合作时如何分配合作所得收益，即收益分配问题［7］;非合作博弈是研究人们在利益相互影响局势下如何决策使自身收益最大，即策略选择问题［6～8］。博弈可用三要素表示

式中 N 为博弈参与人集合，S 为参与人可选策略集合，U为在给定策略S 情况下参与人的收益［8］。

2.2 基于博弈论定位算法模型

为实现高精度节点定位，定位过程包括初始定位阶段和求精阶段。若未知节点存在邻居锚节点或2 跳锚节点［9，10］，在锚节点覆盖区域的交集取一定数量点，将点坐标平均值作为该未知节点的初始坐标。

定位求精阶段，节点多次重复或迭代定位［10，11］。所有节点参与博弈，构建非合作博弈［8］模型。锚节点自身位置已知，即已有最优策略，无须再调整;未知节点不断调整策略使自身收益更高。博弈结束后进入平衡状态，即单个节点独自改变策略并不能增加自身收益。

1)收益函数构造

设(exi，eyi)，(exj，eyj)为节点i，j 的估计坐标，lij为估计坐标间距离，dij为实际测定距离，εij为lij与dij的差值，则有

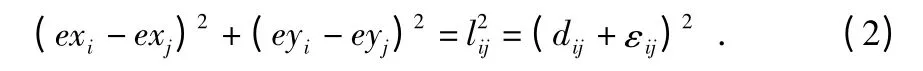
若节点i，j 的估计坐标与实际坐标接近，则意味着εij很小，定位更精确。构造函数

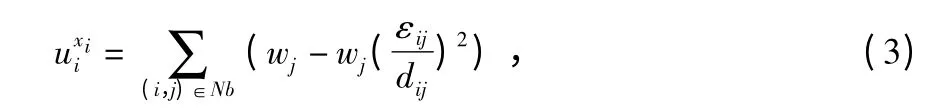
当式(3)累加项的第二项最小，即εij为零时，函数取最大值，如式(4)

此时节点定位结果与真实情况一致。

2)参与者与策略空间

基于定位的博弈模型中，参与者是所有节点的集合，用N={1，…，m}表示。设Xi表示第i 个参与者的策略集，即节点i 可选估计坐标点的集合。记^i=N/i，即^i 表示参与者集合中除i 以外的其他参与者集合［9］，如下式集值映射关系

式中 X 为局中所有策略空间集合，ui为参与者i 的收益函数。

3)基于博弈论定位模型的纳什平衡点

定理1 对参与者集合N 中任意参与者i，设其策略空间集Xi是Hausdorff 局部凸空间Ei中的非空凸紧集，ui∶X→R连续，且任意x^i属于)在Xi上拟凹连续，则此博弈的纳什平衡点存在［7，8］。

［8］给出了定理1 及其证明过程，而定位博弈纳什平衡点存在性分两点来证明:1)X 是Rn中的非空凸紧集［7］;2)ui∶X→R 连续，xi→ui(xi，x^i)在Xi上拟凹连续［8］。证明过程如下:

1)X 中所有策略的取值都是在一定限制区域内可连续的，所以，X 是Rn中的非空凸紧集。

2)收益函数xi→ui(xi，x^i)在Xi上拟凹连续的判定只需证明函数可微。参与者i 在选择策略xi情况下，对收益函数(式(3))求二阶导数

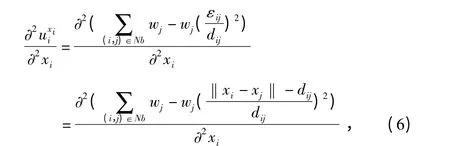
综合考虑两项因素，此博弈存在纳什平衡点。

3 基于博弈论的定位算法实现

假设参与者节点都是理性的，均追求收益最大化，定位过程步骤如下［12，13］:

1)在指定二维区域随机部署N 个未知节点和M 个锚节点。部署完成后节点开始相互通信，通信半径为R。

2)锚节点广播自身的位置信息数据报，其邻居节点接收并转发，数据报只转发一次。

3)未知节点收集两个锚节点的坐标信息(没有一跳锚节点才使用两跳锚节点信息)。

4)初始化未知节点坐标。若未知节点收集到两个锚节点的数据，则以两个锚节点的坐标为圆心，到未知节点距离的1.25 倍为半径画圆，如图2，在两圆的交区域取p 个点，坐标取平均值后作为未知节点的初始坐标;否则，等待下一轮定位。

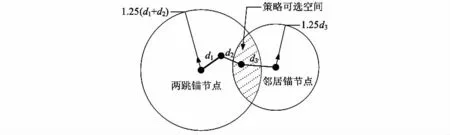
图2 采样区域示意Fig 2 Sampling area illustration

5)采用基于博弈论的定位算法对初始化后的节点进行优化求精，如下伪程序:

4 仿真与分析

为分析算法性能，利用Matlab 7.1 进行仿真实验。

网络平均定位误差定义如下

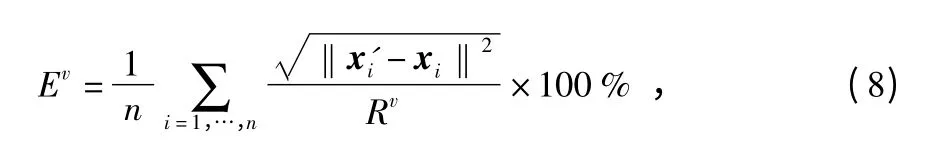
式中 n 为网络中未知节点个数;v 为网络标号;i 为第i 个未知节点;x'i为节点i 的估计坐标矩阵;xi为节点i 的实际坐标矩阵;Rv为节点的通信半径;Ev为网络v 的平均定位误差。

规定150 m×150 m 的矩形为仿真区域，随机部署100 个未知节点和30 个锚节点。如图3，节点通信半径为30 m，空心圆点表示未知节点实际位置，星号表示未知节点估计位置，实心三角号表示锚节点位置。图3(a)为初始化后节点定位结果，误差率高达54.78%;图3(b)为优化后的节点最终定位结果，误差率仅为7.17%，网络边缘未知节点因连通度比中心未知节点低，定位精度稍有降低，但总体效果良好。

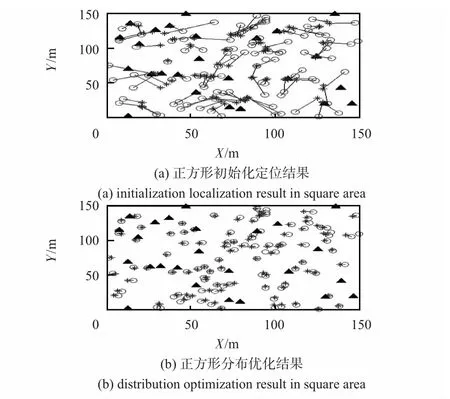
图3 正方形分布节点定位结果Fig 3 Localization result of nodes distribution in square area

在140 m×500 m 的矩形区域中传感器节点呈带状分布，节点密度、锚节点比例和节点通信半径与图3 相同。图4(a)为初始化后节点定位结果。图4(b)为优化后的节点最终定位结果。

在100 m×500 m 的矩形区域中使传感器节点呈条形分布，节点密度、锚节点比例以及节点通信半径与图3 相同。图5(a)为初始化后节点定位结果，图5(b)为优化后的节点最终定位结果。

为分析通信半径对定位精度和节点定位覆盖率的影响，在通信半径由小到大变化时，观察定位情况。随机试验20 次求节点定位误差和覆盖率平均值。

图6 表示节点定位覆盖率随通信半径R 的变化情况，R越大，节点覆盖率越高。当节点通信半径增大时，网络连通度增加，邻居节点增多，有利于提高节点定位覆盖率。

图7 表示节点定位误差随通信半径R 的变化情况，R增大时，定位误差降低。通信半径越大，与待定位节点直接通信的未知节点和锚节点数目增加。在与周围节点进行博弈过程中，更易于找到最优策略。

图4 带状分布节点定位结果Fig 4 Localization result of nodes in zonal distribution

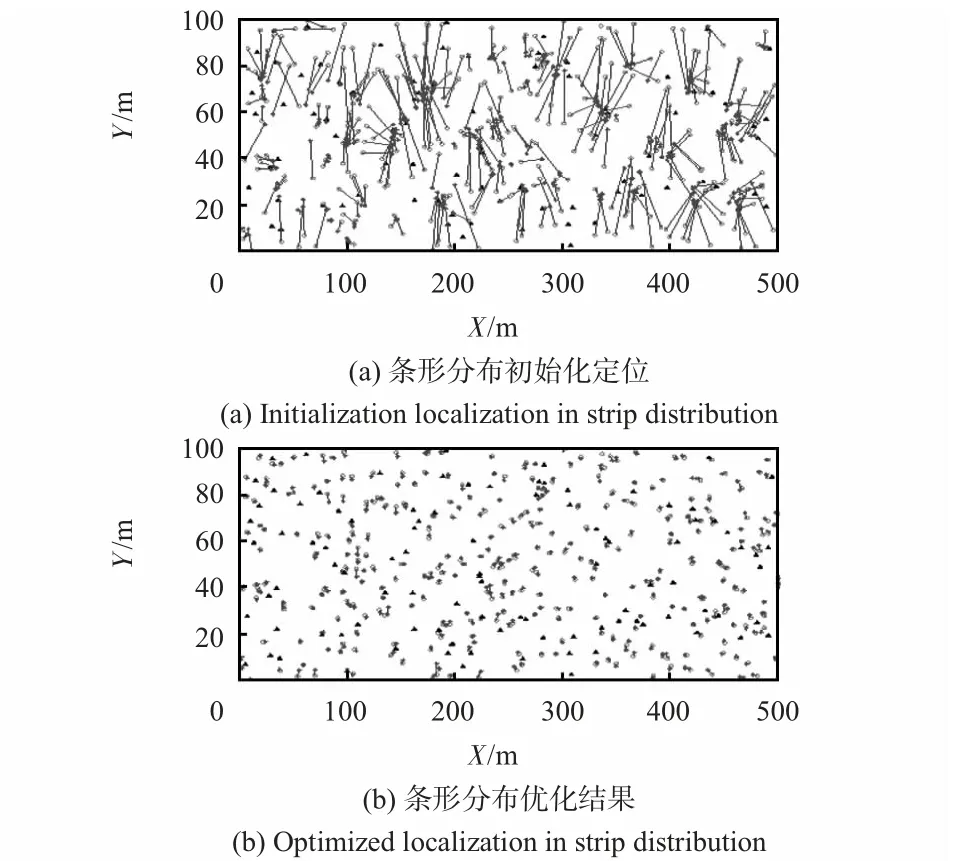
图5 条形分布节点定位结果Fig 5 Localization result of nodes in strip distribution

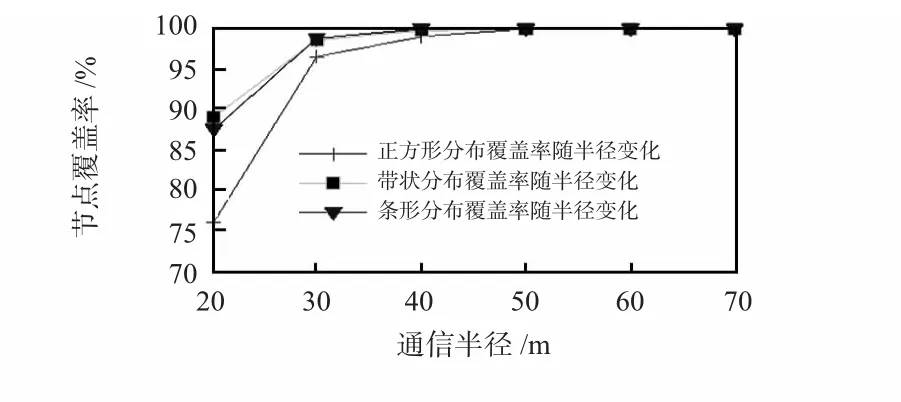
图6 节点定位覆盖率随通信半径变化Fig 6 Change of node localization coverage rate with communication radius

5 结 论

本文针对基于三峡库区水环境监测的大规模带状无线传感器网络，将博弈理论和优化算法应用于节点定位问题，建立节点定位优化算法模型。结合三峡库区特点，对不同区域形状分布下的网络进行定位仿真实验。实验结果表明了算法的可行性和高效性，在不增加硬件开销的情况下提高了定位精度和节点覆盖率。

图7 节点定位误差随通信半径变化Fig 7 Change of node localization error with communication radius

参考文献:

［1］ 毕海普.三峡库区突发水污染事故的数值模拟及风险评估研究［D］.重庆:重庆大学，2011.

［2］ 季富政.长江三峡地区概貌［J］.重庆建筑，2010(9):1－7.

［3］ 刘玉邦，梁 川.长江上游水资源保护分区研究［J］.中国农村水利水电，2009(4):10－14.

［4］ 刘昊灵，仲元昌，杨 柳，等.基于三峡库区水环境监测的WSNs 信息融合算法［J］.传感技术学报，2012，25(12):1761－1765.

［5］ 仲元昌，宋 扬.大规模无线传感器网络自适应节能路由算法［J］.计算机工程与应用，2013，49(1):89－93.

［6］ 康 晶.基于博弈论的无线传感器网络节点间通信的研究［EB/OL］.北京:中国科技论文在线.［2011—01—12］.http:∥www.paper.edu.cn/releasepaper/content/201101－557.

［7］ 黄 河.各向异性无线传感网络节点定位问题研究［D］.合肥:中国科技大学，2011.

［8］ 俞 建.博弈论与非线性分析［M］.北京:科学出版社，2008:74－113.

［9］ Kulkarni R V，Venayagamoorthy G K，Cheng M X.Bio－inspired node localization in wireless sensor networks［C］∥IEEE International Conference on Systems，Man and Cybernetics，SMC 2009，IEEE，2009:205－210.

［10］Sivakumar S，Venkatesan R，Karthiga M.Error minimization in localization of wireless sensor networks using genetic algorithm［J］.International Journal of Computer Applications，2012，43(12):16－20.

［11］Niewiadomska－Szynkiewicz E.Localization in wireless sensor networks:Classification and evaluation of techniques［J］.International Journal of Applied Mathematics and Computer Science，2012，22(2):281－297.

［12］章 磊，段莉莉，钱紫鹃，等.基于遗传算法的WSNs 节点定位技术［J］.计算机工程，2010，36(10):85－87.

［13］马 震，刘 云，沈 波.分布式无线传感器网络定位算法MDS—MAP(D)［J］.通信学报，2008，29(6):57－62.