低频振动对星敏感器成像影响分析

邓长智，王宏力，陆敬辉，崔祥祥，姜 伟，乔 兴

(第二炮兵工程大学，陕西 西安710025)

0 引 言

星光制导技术是一种依靠星敏感器实现高精度绝对姿态测量的新型自主导航技术，在航天器姿态测量与控制中发挥着越来越重要的作用［1］。其中，以捷联方式安装的星敏感器因其具有结构简单、可靠性高、启动时间短、成本低、可维修性强等优势得到广泛应用［2］。星敏感器的核心部件是CCD 相机，在工程实际中，星敏感器成像过程除受到光学系统的衍射、探测器采样、大气的扰动［2］等因素影响外，航天器飞行过程中的复杂振动环境也降低了星敏感器成像质量。其中，振动影响造成的星点拖尾和扩散现象更是限制了导航星提取的精度，甚至可能导致星图无法正常提取［3］。因此，开展振动对星敏感器成像影响分析，对于提高星光制导的性能有着重要的意义。

目前，许多学者围绕振动对星敏感器星图成像问题开展了研究，文献［4～6］结合振动对星图的影响机理进行了一定的分析，但没有针对影响星敏感器成像振动的频率加以区分;文献［7］分析振动频率的不同会对普通相机成像过程带来不同影响，却没有结合星图成像的特点，涉及低频振动对星图成像的分析不够详细。此外，不同振动频率的振动会造成不同程度的模糊图像，低频振动的振动周期远小于曝光周期，且有着很强的随机性，也比高频更普遍［8］。这些低频振动与航天器主体的姿态运动高度耦合，严重制约了星敏感器的工作。

本文从星敏感器星图成像机理出发，针对几种典型的低频振动形式，分析了典型低频振动对星敏感器的影响，并结合模拟星图进行了仿真验证。

1 六自由度星敏感器振动

航天器在空间中的运动可用六个自由度进行描述［9］，即沿x，y，z 三个直角坐标轴方向的平动自由度和绕这三个坐标轴的转动自由度，按照这六个自由度将航天器在空间中的振动分解为沿星敏感器坐标系的坐标轴OX，OY，OZ三轴的线振动和绕三轴的角振动，OZ 方向为光轴方向，OX，OY 方向垂直于光轴方向。每个轴向上的简谐线振动、角振动均可表示为S(t)=Scos(2πt/T0)(线振动)，θ(t)=D(θ)cos(2πt/T0)(角振动)。

航天器的低频线振动和角振动认为其频率足够低，以日本NASDA 的ETS—VI 卫星振动测量试验为例，卫星角振动频率在0.39 ～250 Hz 范围内的振动能量83.6%集中在0.39 ～10 Hz 之间［10］。星敏感器的曝光时间T0仅仅为振动周期Te的一小部分，因此，可以将［0，T0］时刻内的周期为Te简谐振动近似看做匀速线性的运动，形式为S(t)=vt，t∈(0，T0)，(T0≪Te)和θ(t)=ωt，t∈(0，Te)，(T0≪Te)。

2 振动对星图成像影响的机理分析

2.1 点扩散函数

运动图像的成像过程，通常采用点扩散函数PSF 进行描述［11］

空间域

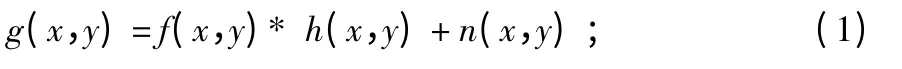
频率域

设g(x，y)为振动条件下的模糊星图，f0(x，y)表示静态条件下的星图，hn(x，y)为各种线振动和角振动的点扩散函数PSF，即线振动点扩散函数、非光轴角振动点扩散函数和光轴角振动点扩散函数，并假设噪声n(x，y)为高斯白噪声，即为:g(x，y)=f0(x，y)*h1(x，y)…h5(x，y)+n(x，y)。

若在振动的模糊方向为θ、模糊长度为L 已知的情况下，振动过程点扩散函数h(x，y)及其傅立叶变换H(u，v)可表示为

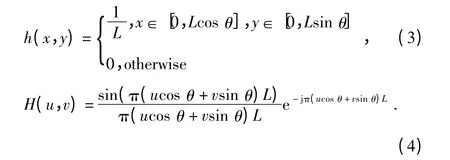
2.2 线振动点扩散函数

将线振动按照三个轴向进行分解，对于光轴OZ 轴，OZ轴向上的线振动只是造成了星敏感器相对于成像平面沿着OZ 轴方向的上下平动，不会影响成像点的位置变化，因此，不考虑OZ 轴向上的线振动对星图成像的影响。成像平面内OX，OY 轴是正交且对称的，其影响机理相同。在图1 中以OX 轴向线振动为例进行分析，星敏感器的线振动S(t)=vxt作用于CCD 的中心，得到的对应于成像平面的像点的位移为Lx。

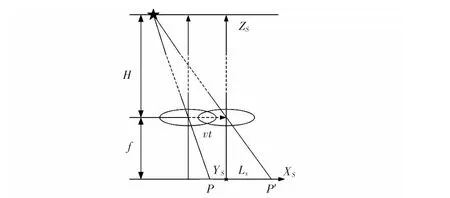
图1 线振动星图模糊Fig 1 Star image blur caused by linear vibration

分析线振动成像的点扩散函数，模糊方向为θ=0(cos θ=1)，模糊长度L=Lx，由几何成像关系可得:即

OX 轴上的线振动点扩散函数模糊方向为θ=0，模糊尺度为Lx=(1+f/H)vxt。同理，OY 轴线上的点扩散函数模糊方向为θ=90°，模糊尺度为Ly=(1+f/H)vyt。

2.3 非光轴角振动点扩散函数

OX，OY 轴为非光轴方向，沿着非光轴的角振动会造成成像CCD、入射光线和光轴OZ 轴绕着非光轴转动，并使得成像像点也发生偏移。将这种相对运动等同于光心不动，CCD、入射光线、光轴OZ 轴绕着CCD 的中心发生旋转Δα。

现以图2 中以X 轴上的点扩散函数进行分析，其模糊方向为θ=0(cos θ=1)，模糊长度为Lx，设Lx=ΔL，ΔL=|PP'|=|OP'|－|OP|，|OP|=ftan α，|OP'|=ftan(α+Δα)，则，ΔL=ftan(α+Δα)－ftan α，根据可微的表示式可得:即有

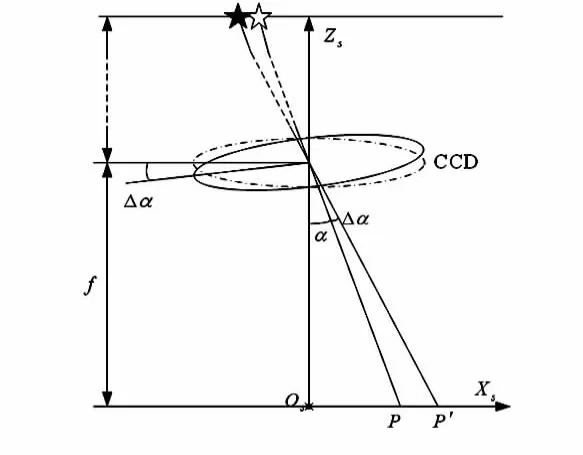
图2 OX 轴角振动星图模糊Fig 2 Star image blur caused by OX axis angular vibration

2.4 光轴角振动点扩散函数

OZ 轴是星敏感器的光轴，沿着OZ 轴向的是沿着光轴的角振动，对成像的影响与非光轴的角振动性质不同。由于运动的相对性，入射光线不变的情况下，星敏感器沿着OZ 轴向的角振动Δγ，可以等同于星敏感器不动，入射光线绕着OZ 轴的角振动Δγ，成像像点在成像平面上，也会沿着其光轴的矢量半径进行角振动Δγ 的旋转。

如图3 所示，像点P 点(点(x，y))经角振动Δγ 作用运动至P'点，两点在，夹角为Δγ=ωΔt 的圆弧上。过P 点作切线PN，交OP'于N。对模糊方向θ，θ 为PP'和X轴的夹角。由图可知，由于曝光时间比较短，角振动造成的角度偏差比较小，可以忽略不计，近似认为的模糊方向θ 和的模糊方向是一样的，即。对于模糊尺度L，有由图可知L=2Rsin(Δγ/2)，S=RΔγ。

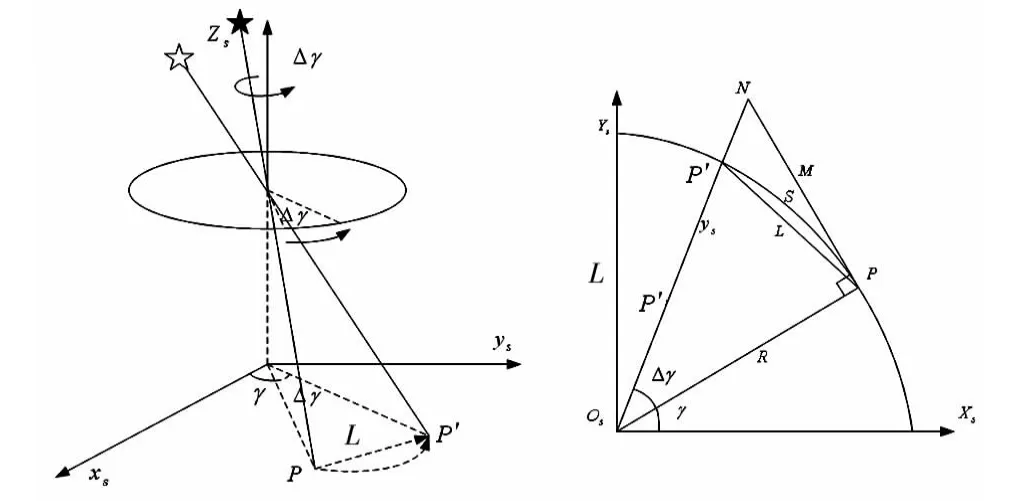
图3 OZ 轴角振动星图模糊Fig 3 Star image blur caused by OZ axis angular vibration

3 仿真分析与结论

以某型星敏感器为参考开展仿真，其参数设置参见表1。

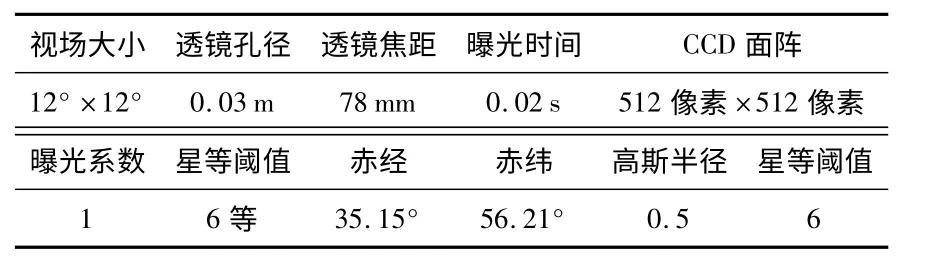
表1 星敏感器工作参数选择Tab 1 Working parameters selection of star sensor

3.1 线振动与非光轴角振动对星图成像仿真分析

静态条件下的模拟星点，呈高斯分布，共5 像素×5 像素。经过低频线振动vx=20 m/s 时，可得如图4 所示的单一星点的仿真星图，呈8 像素×5 像素的条状星点，在纵轴方向上进行扩散。同样，经过低频振动vx=30 m/s 时，可以得到10 像素×5 像素条状星点。

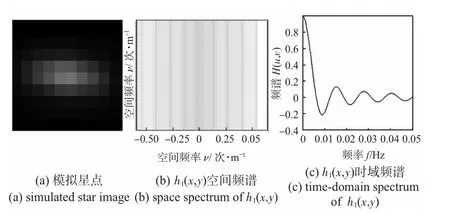
图4 线振动对星图成像影响仿真Fig 4 Simulation of impact of linear vibration on star imaging

角振动对星图影响的仿真如图5 所示，选取了第一象限内的成像星图，对于整幅星图上的星点都是在纵轴方向上进行了扩散;对于不同的横坐标位置的星点受到振动后变化几乎没有差别。

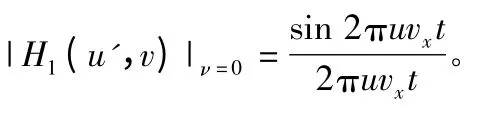
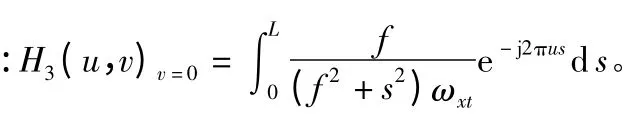
3.2 光轴角振动对星图成像仿真分析

选择OZ 轴线上的角振动为1 rad/s 时，仿真星图如图6所示，相对于静态星点，不仅仅是产生了扩散，对于不同位置的星点有着不同的旋转角度。

OZ 轴线上的角振动对于星图的影响，不仅仅是体现在模糊尺度，同时也因为星点和振动的变化有着变化的模糊方向θ=π/2－arctan(y/x)。因此，OZ 轴向的角振动不仅仅会对星点在扩散过程中造成与3.1 中相同的弥散半径，还会带来绕光轴角度上的旋转。

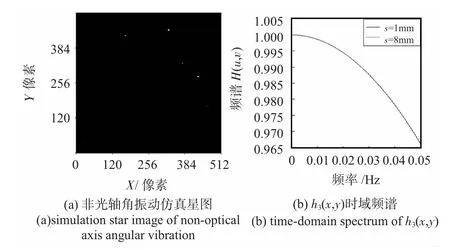
图5 非光轴角振动对星图成像影响仿真Fig 5 Simulation of impact of non-optical axis angular vibration on star image

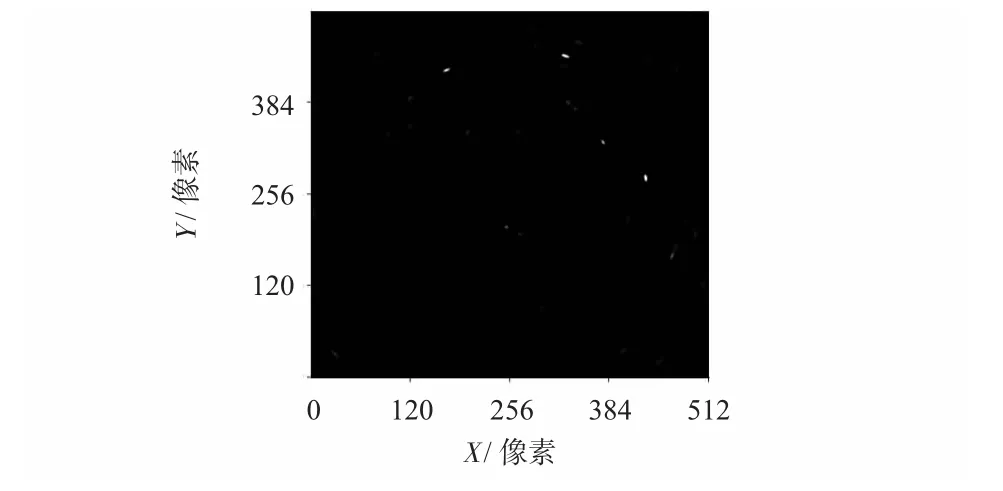
图6 光轴角振动仿真星图Fig 6 Simulation star image of impact of non-optical axis angular vibration

4 结束语

本文从对影响星敏感器工作的低频振动信号入手，结合了星敏感器的成像机理和低频振动信号的特点，从理论上分析了低频振动的影响，并进行了仿真验证，说明不同振动对星图成像作用方式的不同。

［1］ 陈金枝.天文导航与星光导航［J］.舰船科学技术，2001(1):62－65.

［2］ 张天光，王秀萍，王丽霞，等，译.捷联惯性导航技术［M］.北京:国防工业出版社，2007.

［3］ 庄绪霞.平台运动对星载TDICCD 相机成像质量影响分析与仿真［D］.哈尔滨:哈尔滨工业大学，2011.

［4］ 温昌礼.平台角振动对图像测量系统的影响［D］.长沙:国防科学技术大学，2006.

［5］ Hadar O，Fisher M，Kopeikan S.Image resolution limits resulting from mechanical vibrations.Part 3:Numerical calculation of modulation transfer function［J］.Opt Eng，1992，31(3):581－589.

［6］ 吴小娟，王新龙.星图运动模糊及其复原方法［J］.北京航空航天大学学报，2011，37(11):1338－1342.

［7］ 耿文豹，翟林培，丁亚林.振动对光学成像系统传递函数影响的分析［J］.光学精密工程，2009，17(2):314－320.

［8］ Morio Toyoshima，Yoshihisa Takayama，Hiroo Kunimori.Inorbit measurements of spacecraft microvibrations for satellite laser communication links［J］.Optical Engineering，2010，49(8):1－10.

［9］ 于大泳.六自由度运动模拟器精度分析及其标定［D］哈尔滨:哈尔滨工业大学，2006:6.

［10］张博文，王小勇，胡永力.微振动对高分辨率空间相机成像影响的集成分析［J］.航天返回与遥感，2012，33(2):60－65.

［11］张燕妮.离焦模糊图像复原方法的研究［D］.大连:大连理工大学，2005.