随机振动的描述及其试验与仿真

2015-03-25赵润生

环境技术 2015年3期

吴焕，赵润生，唐勇

（中认英泰检测技术有限公司，苏州 215104）

引言

随机振动是未来任何一给定时刻的瞬时值都不可预先确定的一种机械振动。它的运动规律无法用确定函数，只能用概率与统计方法描述。随机振动从振动单次现象观察来看存在不确定性，但根据相同的条件下多次测试结果的总体分析，其统计特征为确定的。通常随机振动探讨的问题有：确定系统响应统计特性之“预测”问题，估计系统性能之“识别”问题以及寻找外部的激励信息之“测量”问题[1]。

工程上用随机振动试验来确定元器件和设备经受规定严酷等级的随机振动能力，国内目前能进行随机振动试验的检测机构非常多，但能完成较大量级随机振动试验的单位较少。

随着有限元技术的发展，随机振动也可以通过计算机进行有限元仿真。经过试验验证的有限元分析方法可以用来分析结构在随机激励下的响应，研究结构在承受一定严酷等级随机振动后的失效模式，在此基础上对结构进行优化设计，缩短了结构设计周期，降低了设计成本。

1 随机振动的描述

随机振动和确定性振动有本质的不同，不能用时间的确定性函数来描述。在幅域上，随机振动通过概率分布函数、概率密度函数、均值、均方值、方差等来描述；在时差域上用相关函数、相关系数来描述；在频域上则通过功率谱密度函数来描述[2]。

1.1 随机振动的幅域描述

1）概率密度函数

如图1所示的随机信号，描述的是信号幅值随时间的变化，幅值落在 x到x +Δx 区间内的总时间为：

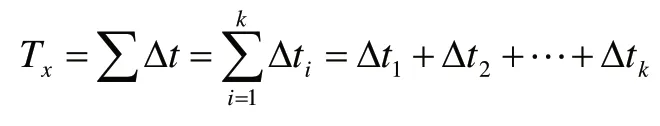
则幅值落在该区间内的概率为：

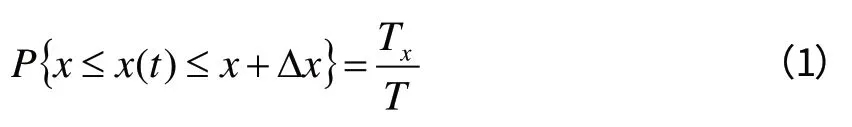
定义概率密度函数为：

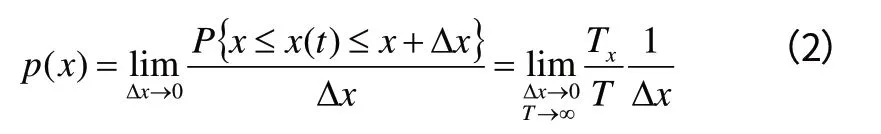
由式（2）可以看出，概率密度函数是概率相对于振幅的变化率，因此可以从对概率密度函数积分而得到概率，即：

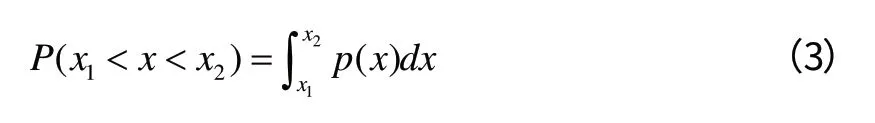
式（2）亦表明概率密度函数是概率分布函数的导数，它给出了随机信号沿幅值域分布的统计规律。不同随机信号有不同的概率密度函数图形，工程上最常见的也是应用最多的是正态分布的概率密度函数图形，如图2所示。

2）均值

随机信号{ Xn}的均值定义为其随机变量Xn的数学期望：

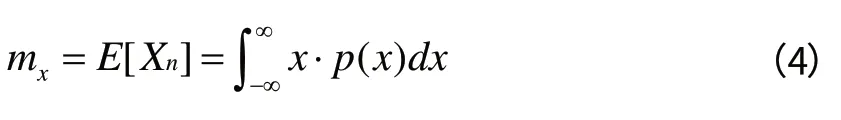
均值是随机变量的一阶矩，可理解为信号的直流分量。

3）均方值

随机信号{ Xn}的均方值定义为其随机变量Xn模的平方的数学期望：

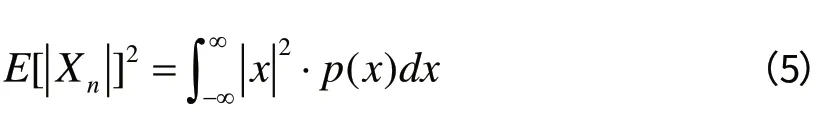
均方值是随机变量的二阶矩，可理解为信号的平均功率，表达了信号的强度。

1.2 随机振动的频域描述

信号频域描述的目的是判断一个信号过程由哪些频率成分构成。对于确定性信号，若信号为周期信号，可用傅里叶级数展开来分析周期信号的频率成分；若为非周期信号，可用信号本身的傅里叶变换来对信号进行频域分析。而对于随机信号，不能直接对其进行傅里叶变换，采用功率谱密度函数进行频域描述。

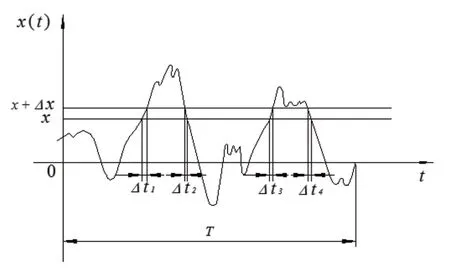
图1 随机信号示意图

根据巴塞法尔定理，在时域中计算的信号总能量等于在频域中计算的信号总能量，即：

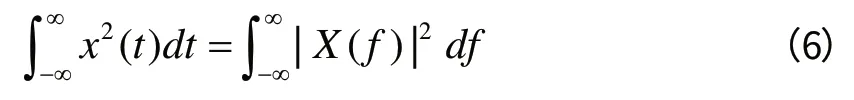
对于上式等号左边的积分，均值不为零的随机信号不是平方可积的，在这种情况下就没有傅里叶变换。维纳-辛钦定理（Wiener-Khinchin theorem）提供了一个简单的替换方法，如果信号可以看作是平稳随机过程，那么功率谱密度就是信号自相关函数的傅里叶变换，记为Sx(f)，结合自相关函数的定义，进一步推导得：

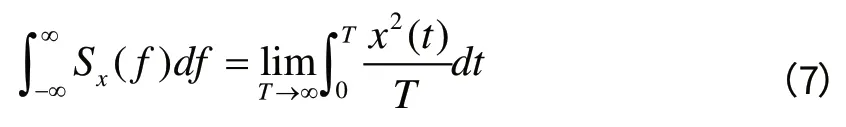
2 随机振动试验

2.1 试验简介

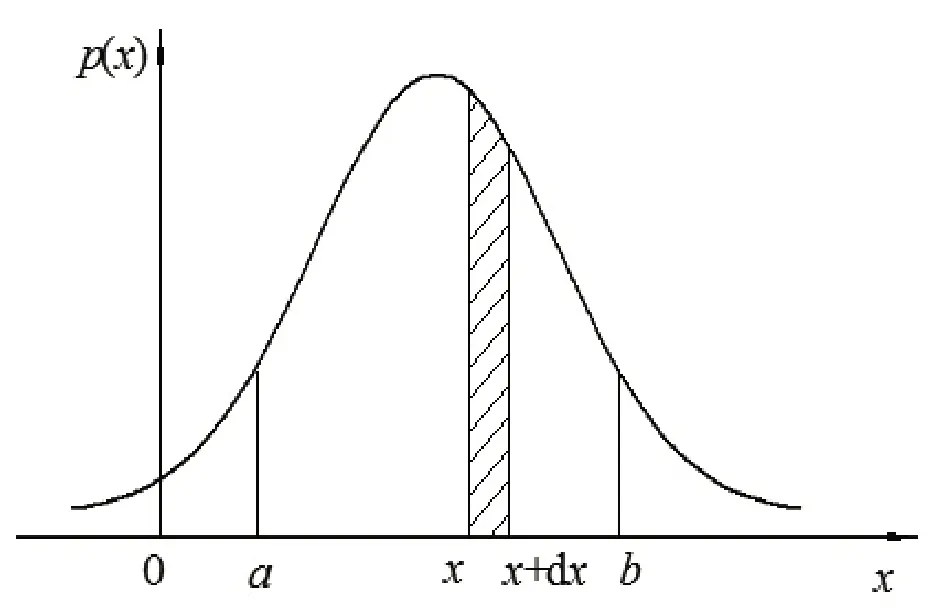
图2 正态分布概率密度函数示意图

随机振动试验适用于使用中可能受到随机性振动条件影响的元器件和设备。试验目的在于确定机械弱点和（或）规定性能是否下降，并结合有关规范使用这些信息来决定试验样品是否接收。工程上随机振动试验采用振动台实现，样品通过夹具固定在振动台台面上，随机振动信号由振动控制仪给出，经过功率放大器传递至振动台，实现振动激励，加速度计将振动信号反馈至控制系统，实现闭环控制，如图3所示为随机振动试验示意图。

随机振动试验方法已列入国家标准GB/T 2423，以扩大现行的正弦振动试验GB/T 2423.10。随机振动试验是一种比较接近于实际环境中存在的振动类型的试验方法，并且在试验样品中产生的效应比较接近于使用中可能发生的效应。当实际环境大致为随机振动时，只要经济上合理就应采用随机振动试验，因为正弦振动和随机振动对样品失效机理的影响方式并不相同[3-4]。

2.2 试验条件和相关试验参数计算

随机振动的试验条件包含试验频率区间、试验谱形和量级、试验时间以及试验方向。试验谱形和试验量级经常用表格的形式或者加速度功率谱密度曲线的形式给出。图4为用功率谱密度曲线表示的典型随机振动的试验条件：

2）加速度功率谱密度斜率（dB/oct）按照下式计算：

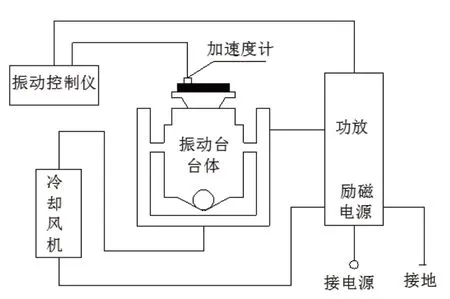
图3 随机振动试验示意图

3）加速度均方根值（grms）的计算

由功率谱密度的定义可知，功率谱密度曲线下的总面积即为随机信号的总功率，再求其算数平方根，即可得到加速度均方根值。面积A1、A2、A3计算如下：

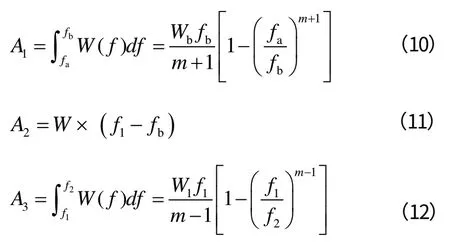
式中m=N/3，若N=3则m=1时，必须采用以下降谱计算公式：

则加速度总均方根值为加速度功率谱密度曲线下总面积的算术平方根，即：

加速度总均方根值是随机振动量级的衡量。

2.3 试验再现性

在所有环境试验方法国家标准中，特别是对鉴定试验或验收试验，以及有关方面（例如电子元器件的供方和需方）打算对同型号试验样品进行的试验，都要求有一定等级的再现性。

一是研究制订更加有效的政策，扶持“金属表面无磷处理”“中水回用”“再生水、雨水综合利用”等项目，以发挥示范项目的作用；二是通过 “多水源、多用户的优化配置”等方面研究，进一步加强水资源管理能力；三是继续加大农村供水管网改造力度，2014年将完成城区及乡镇26个村的老旧供水设施的改造,将农村供水管网漏损率降低到22%；四是加快实施居民自来水阶梯水价制度，创建一批节水型示范机关、学校、企业、医院、居民小区；五是加快新建、扩建4个集镇污水处理厂，将全市的污水日处理能力从现在的9.5万t提高到22万t。

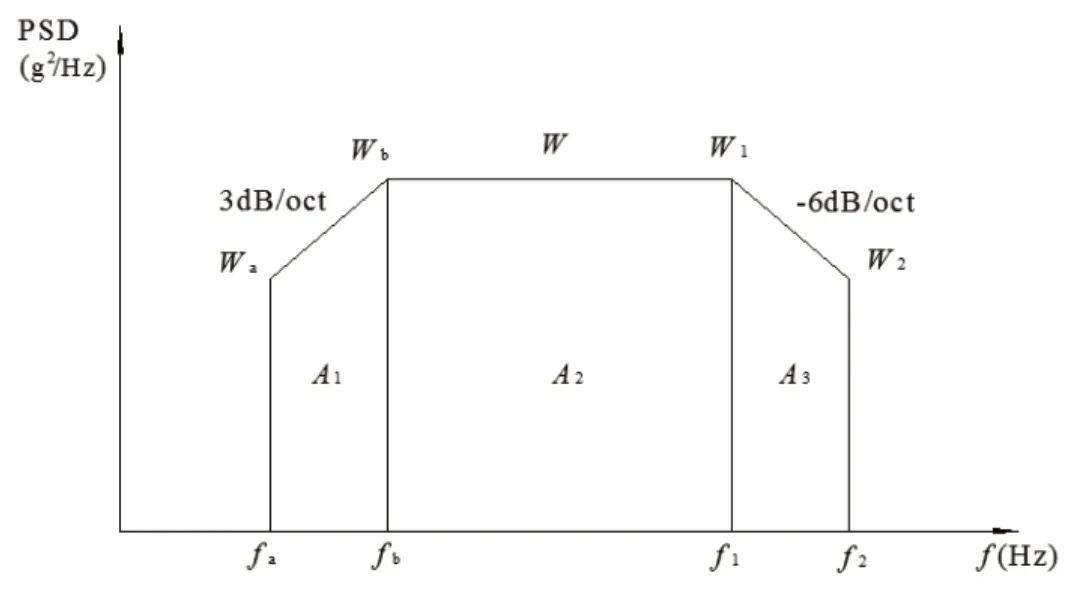
图4 功率谱密度曲线图

随机振动试验的再现性不是指试验与实际环境之间的再现性，而是指由不同的人在不同场合下进行试验时所得结果的一致性。随机振动的再现性分为高、中、低三个等级，不同等级对应的试验容差不同。

低再现性试验方法可能比其他方法要简单和便宜。高再现性试验给出相对高的再现性，但一般都比较复杂，可能需要更贵重和更先进的试验设备，还由于要求附加的测试而使试验的时间较长。只有当绝对必要时才要求采用高再现性试验。

再现性的选取不应高于试验样品推荐应用时所必要的再现性。

3 随机振动的有限元仿真

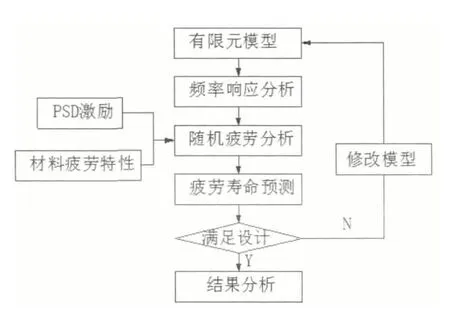
图5 随机振动有限元分析流程

随着社会工业发展以及经济水平逐渐提高，对各种结构的可靠性、安全性要求也越来越高，其中结构的振动问题为影响结构可靠性、安全性的重要因素。机械设备、桥梁、建筑物、输电铁塔等各种结构在实际应用中，难免受到地震、冲击、波浪、风载等外界的随机激励，确保结构在振动激励下的可靠性、安全性十分必要。

通过随机振动试验，在实验室中就能模拟结构经受外界随机激励，得到结构的响应或失效模式。但对于大型结构、建筑、桥梁等，需在设计阶段就对其抗振能力进行评估，确保结构具有足够的安全性才投入生产和建造，利用随机振动试验无法实现。采用有限元技术，在计算机中就能模拟结构经受随机振动激励时的响应，如图5所示，结合材料的疲劳特性，还能预估结构的使用寿命[5]。

如图6所示为某输电铁塔的随机振动有限元分析过程。在软件ANSYS Workbench中建立输电铁塔的有限元模型（图6a），对其进行模态分析，得到其固有频率和振型，即输电铁塔自身的振动特性（图6b）；输入随机振动功率谱密度曲线（图6c），通过模态合并，计算出结构在给定随机激励下的响应（图6d）。

随机振动有限元分析流程简单，软件操作便捷，分析结果可靠性高。大批有限元软件的问世使各种非线性问题、耦合场问题的分析成为可能，有限元技术在工程中应用愈来愈广泛。