含裙板锚泊浮筒的动力响应分析

郑妍颖

(华南理工大学土木与交通学院 , 广州510640)

1 前言

伴随着石油的需求总量不断加大，海洋石油开采已经成为人们获取能源的重要方式之一。深海油气资源开发是必然的趋势，单点系泊技术已成为海洋工程界的热门课题。陈矗立[1]采用集中质量法模拟计算锚链线，对FPDSO、G-Spar和“挑战号”半潜平台进行运动响应分析；王冬姣[2]采用特征函数展开法、边界匹配法对深海浮式直立圆柱体的水动力系数进行计算；郭霆[3]运用HydroSTAR、Ariane等计算软件对FPSO、SEMI、SPAR、TLP等四种浮式结构的RAO、二阶波浪力和锚链受力进行了分析；单长飞等人[4]借助Matlab 工具，对入射波下的波能采集浮筒进行运动响应特性的综合分析，得到了圆柱形浮筒位移响应幅值、速度响应算子、加速度响应算子与入射波圆频率的关系；李竺霖[5]进行了在特定的海洋环境条件下的一阶运动响应函数、运动谱和统计值分析，并与相应的试验结果进行了比较；王冬姣[6]对由三段索链、浮子或沉子组合而成的多索链复合锚泊系统进行了静力分析，其中采用悬链线方程并忽略作用在锚泊线上的流体动力，但考虑了锚泊线的弹性伸长、索链相连的浮子或沉子的具体尺度作用。

本文借助Workbench，对有裙板的锚泊浮筒系统进行模拟，将锚链分成100段，采用动力分析，根据浮筒各自由度上的动力响应，研究系泊锚链的受力情况，验证了锚链的参数符合安全性要求。

2 锚泊浮筒时域运动方程

锚泊浮筒在风、浪、流作用下的时域运动方程，可表示为：

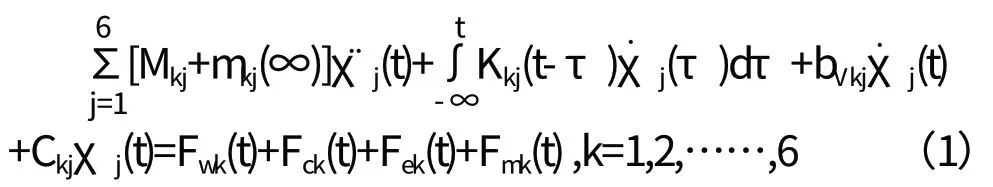
式中：Fwk(t)、Fck(t)、Fek(t)、Fmk(t)分别为作用在浮筒上的风力、流力、波浪扰动力和锚泊力；Mkj为浮筒的质量矩阵；Ckj为静水力刚度矩阵；bVkj为线性粘性阻尼系数矩阵；Mkj(∞)为频率无穷时的附加质量矩阵；Kkj(t-τ)为浮筒的延迟函数矩阵，可通过频域计算中得到的附加质量Akj(ω)和辐射阻尼系数Bkj(ω)计算得到：

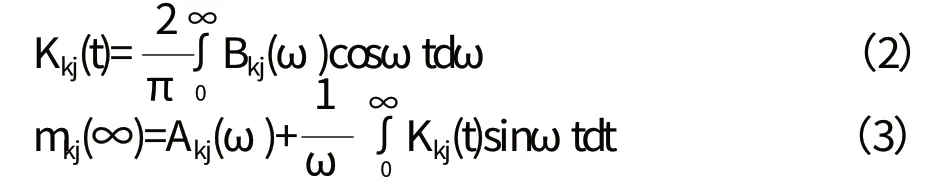
作用在浮筒上的水平风力和流力可按Morison公式计算：

式中：ρa和ρ分别为空气密度和海水密度；Aw和Ac分别为与风速和流速垂直方向的投影面积；Cw和Cc分别为风和流的阻力系数，取1.0；Vw和Vc分别表示相对风速和相对流速；θw和θc分别为相对风速和流速的方向角。

选用PM谱模拟不规则波，作用在浮筒上的波浪载荷可表示为：

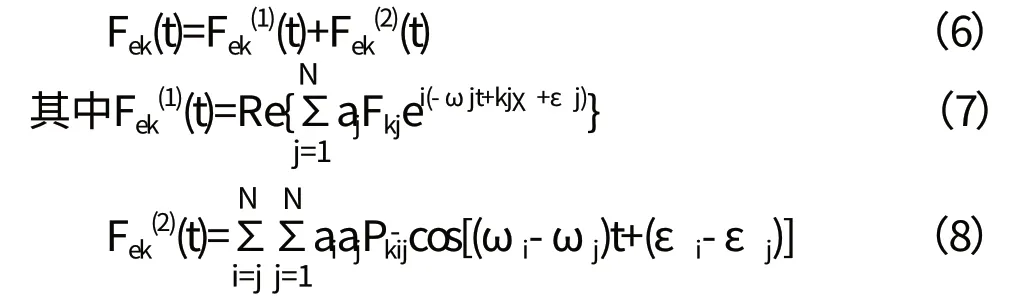
基于Newman近似法，可得：

式中：Fek(1)(t)为作用在浮筒上的一阶波浪载荷；Fek(2)(t)为作用在浮筒上的二阶波浪载荷；Fk为一阶波浪扰动力传递函数。对于任意两个频率组成的双色波，用ai、aj表示双色组成波的波幅值，ωi、ωj为频率，εi、εj为随机相位角；为双色波频率ωi、ωj对应的二阶差频波浪载荷传递函数的实部。

结构物的垂荡bV33和纵荡bV11运动的线性粘性阻尼系数，可用下式[7]计算：

结构物的纵摇运动阻尼系数bV55，可用下式[7]计算：

式中：D 为结构物的基准宽度；L 为结构物的总长度；Cd为莫里森系数；d1、d2分别为结构上下边缘的吃水深度。

3 计算模型

浮筒锚泊系统，如图1所示。水深21.85 m，锚泊浮筒直径为12.0 m，型深5.45 m，吃水3.45 m，裙板直径14.0 m。6根锚链呈散射均匀分布，一端通过止链器与浮筒连接，另一端通过锚桩固定到海底，锚桩与浮筒中心水平距离为274.4 m。锚链类型为非线性的悬链线，长度273.58 m，锚链直径120 mm，拉压刚度为2.37×106kN，单位长度链重为279.68 kg/m，破断强度为13 573 kN，将每根锚泊线划分为100个单元，采用动力分析。10分钟平均风速为50.3 m/s。采用PM谱，有义波高为10.8 m，过零周期14 s，表面流速2.26 m/s。风、浪、流方向均为0°（由锚链4指向锚链1），浮筒水动力计算模型如图2所示。

阻尼矩阵是一个6×6的非零矩阵，其对角线元素对结构的运动起主导作用，本文只计算阻尼矩阵的对角线元素，令其他元素为零，根据浮筒结构的对称性可知b11= b22、b44=b55。由于首摇运动是一个很小的量值，计算时只需给定b66一个足够大的数值。

粘性阻尼计算中各参数的取值，如表1所列。

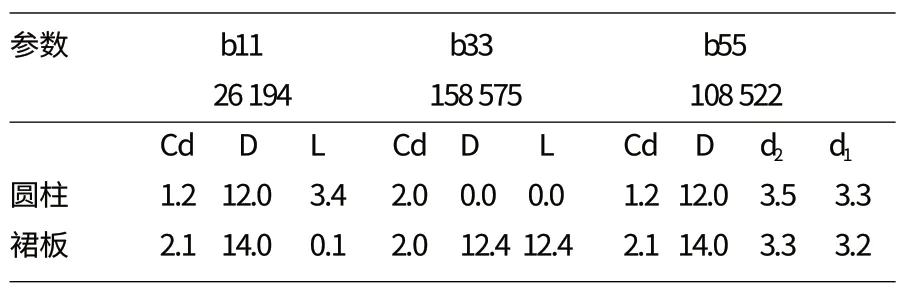
表1 粘性阻尼计算中各参数的取值

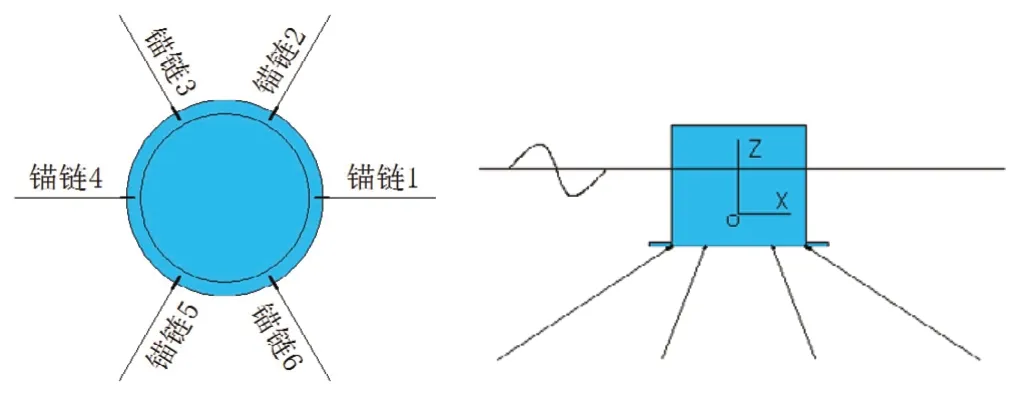
图1 锚泊浮筒

图2 浮筒水动力计算模型

4 计算结果分析

设浮筒的排水体积为V,直径为D,无因次附加质量可表示为:

无因次辐射阻尼系数为：

单位波幅作用下，无因次一阶波浪力可表示为：

单位波幅作用下，水平方向的无因次漂移力可表示为：

波浪入射角为0°，频率区间取0.01 Hz至0.7 Hz。图3和图4为通过频域计算得到的无因次附加质量和辐射阻尼曲线；图5为单位波幅作用下的一阶波浪力；图6为纵荡方向的漂移力。

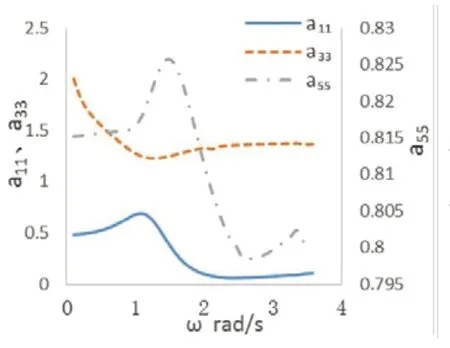
图3 浮筒的附加质量

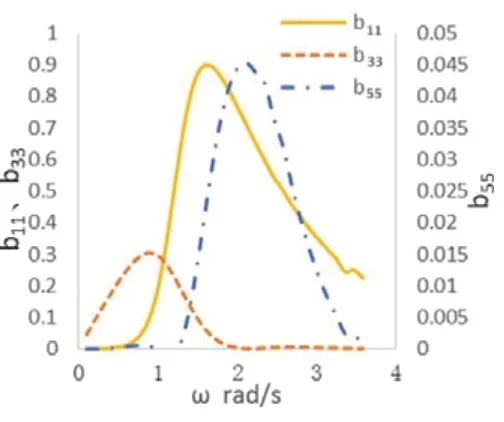
图4 浮筒的辐射阻尼

图5 一阶波浪力传递函数

图6 纵荡方向漂移力曲线图

使用Workbench软件进行时域计算，模拟锚泊浮筒在风向角、浪向角和流向角均为0°时的表现。时域计算时间取3小时（步长为0.05 s），考虑了粘性阻尼和锚链力动力分析，最终得到系泊浮筒各方向的偏移以及系缆绳张力的时历变化曲线。由时域计算所得的各锚链张力计算结果见表2。

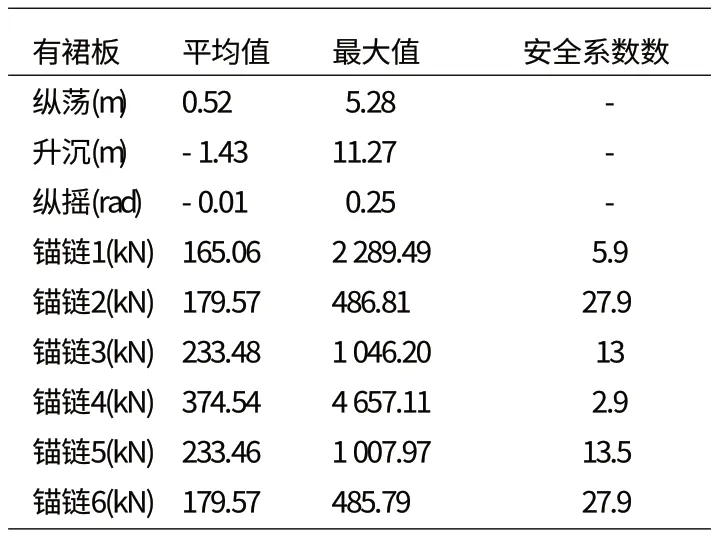
表2 浮筒运动和锚链力统计值

由表中结果可以看出：

（1）当风向角、浪向角和流向角为0°时，浮筒的升沉运动最大值为11.27 m，平均值-1.43 m；纵摇运动最大值为0.25rad，平均值-0.01rad；

（2）由于锚链4与风浪流的来流方向同向，因此所受的拉力最大，其安全系数为2.9﹥1.67，所以该锚链符合API的安全规范[8]。

5 结论

（1）裙板在结构方面起了很好的防撞作用，在严峻的海上环境下可以很好的保护浮筒结构的完整性，从而保证锚泊浮筒性能的持久性；

（2）锚链4与风浪流的来流方向相同，因此所受的拉力最大，其安全系数为2.9，大于规范要求的1.67，因此符合锚链的安全性要求。

[1]陈矗立.深海浮式结构物及其锚泊系统的动力特性研究[D].上海交通大学, 2007.

[2]王冬姣,周晖.深海中浮式直立圆柱体水动力系数研究[J].科学技术与工程,2010,10(1).

[3]郭霆.典型浮式结构水动力性能分析[D].哈尔滨工程大学, 2012.

[4]单长飞,谢永和,李德堂等.单自由度浮式圆柱形波能发电装置的水动力计算[J].船舶工程,2012(Z2):213-216，231.

[5]李竺霖.单点系泊系统低频运动响应研究[D].大连理工大学, 2013.

[6]王冬姣.索-链-浮子/沉子组合锚泊线的静力分析[J].中国海洋平台2007,22(6)：16-20.

[7]李溢涵.海上风机Spar型浮式基础的运动特性研究[D].天津大学, 2011.

[8]American Petroleum Institute.Recommended practice for planning, designing,and constructing fixed offshore platforms[M].American Petroleum Institute,1989.