改进的Monte Carlo算法在碳排放价格预测和收益率分析中的应用

刘大旭

中国人民银行潍坊市中心支行,山东潍坊261000

改进的Monte Carlo算法在碳排放价格预测和收益率分析中的应用

刘大旭

中国人民银行潍坊市中心支行,山东潍坊261000

传统的碳排放价格预测和收益率分析，大多数采用计量经济学方法，对样本数据的真实性和样本数量有着极高的要求。由于Monte Carlo算法具有适合小样本数据量分析和预测精度高的优点，将其用于碳排放价格预测和收益率分析。通过维纳运动方程构建出数学模型，之后结合Monte Carlo算法，模拟维纳运动过程的变化规律，从而实现碳排放价格的预测。通过JB统计量检验和VAR检验表明，针对小样本碳排放价格数据，改进的Monte Carlo算法具有更高的预测精度，对碳排放价格的描述和刻画能力更强，可以用于为碳排放期货交易和价格确定提供科学决策以及为其他经济领域和方向的定量描述和预测提供依据。

蒙特卡罗算法;碳排放;预测

随着全球化气候变暖，对传统石化燃料的碳排放要求日趋严格，清洁能源的使用大势所趋。针对碳排放价格（Price of Carbon Emission Rate，PCER）的预测和收益率分析，国外很多学者研究的重点大多数采用的是计量经济学方法分析碳排放价格的影响因素[1-6]。

由于Monte Carlo算法具有预测精度高、适合小样本量数据的优点，本文将Monte Carlo算法用于碳排放价格预测和收益率分析，结合维纳运动方程的变化规律，实现基于Monte Carlo算法的碳排放价格预测，并进行JB统计量检验和VAR检验。

1 Monte Carlo预测模型

1.1 算法思路

由于大部分PCER价值实质性是一种PCER价格到期回报的期望值的贴现，所以通过模拟PCER价格的多种运动路径，计算每种路径结果下的回报均值之后贴现实现其在整个期间的碳价格的获取。

1.2 算法的改进

为了模拟描述出PCER价格的可能变化过程，本文首先运用维纳过程表示PCER价格的变化过程，之后利用公式（1），运用Monte Carlo算法刻画PCER价格的连续波动方程[7,8]：

式中：St表示t时刻的PCER价格；dz表示均值为0、方差为dt的正态随机变量；σt表示PCER价格变化率的标准差；µt表示PCER价格变化率的均值。

1.3 PCER价格预测

根据连续波动方程公式（1），生产一组随机数ε1，ε2，Λ，εn通过模拟产生如式（2）的价格路径[9,10]：

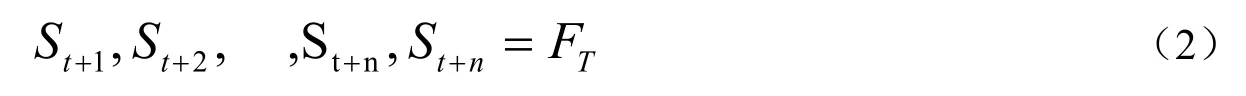
其算法步骤如下：

Step1：MC算法随机产生[0,1]均匀分布的随机数。

Step2：通过密度函数的逆变换将服从[0,1]上均匀分布的随机数转化成一定分布的随机数。

Step3：令dt≈Δt，t、T分别表示当前时刻和目标时刻，那么τ=T-t表示持续期。

Step4：为了产生一系列的随机变量St+i，将持续期分成n个区间，使得Δt=τ/n，并对dS/S在t时间段内进行积分，得到公式（3）[11]：

式（3）中ε服从N(0,1)分布，随机变量S的价格走势，由St出发，按照依次顺序计算出一系列的标准正态随机变量。

Step6：重复上述步骤1000次，获得不同时刻T的1000个模拟价格FT1，FT2，Λ，FT1000，通过该价格序列可以计算出该时刻的分布形式。

2 实证分析

2.1 数据来源

为了验证本文算法的有效性，需要运用现实碳排放价格数据验证，本文中碳排放价格数据来源于欧洲气候交易所[12]。本文选取2014年1月1日～2014年4月30日的104个有效历史数据作为研究对象进行验证，图1表示碳排放原始价格曲线。

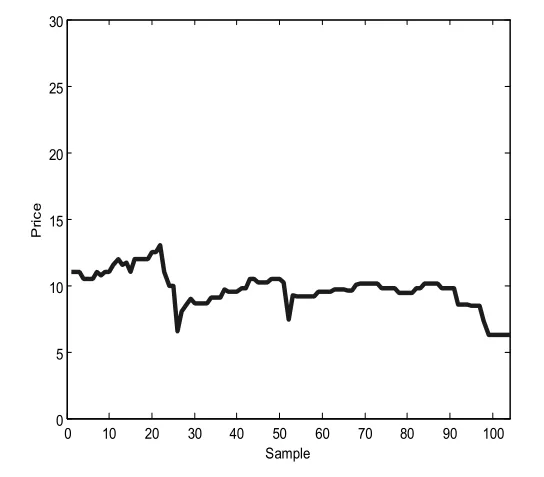
图1 PCER原始价格曲线Fig.1 PCER original price curve

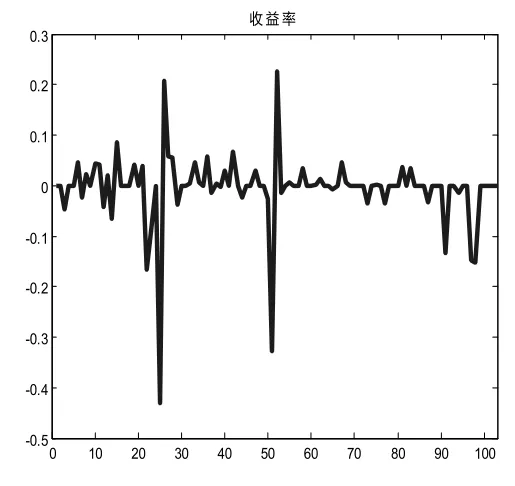
图2 PCER的收益率Fig.2 PCER earnings

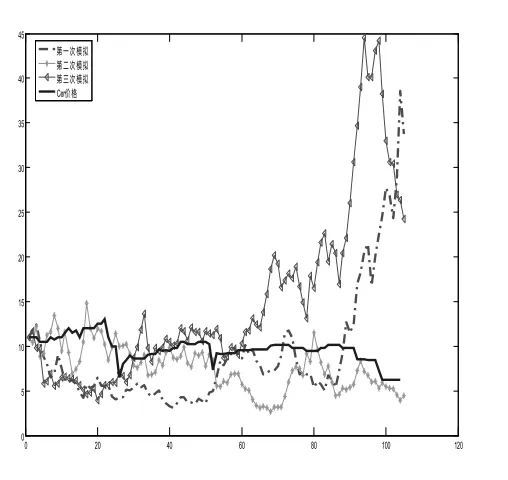
图3 MC模拟的价格走势Fig.3 MC simulation price movements

2.2 MC算法的收益模型和参数

针对布朗运动模型中，价格差存在初始值敏感的问题，本文用价格的变化率替代几何布朗运动模型中的价格差，从而避免布朗运动刻画价格行为的缺陷。

将收集到的104个PCER价格数据作为历史数据，计算出历史收益率的均值µ=-0.00549和波动率σ=0.073557，将均值µ和标准差σ的数值代入几何布朗模型，作为模型的参数。图2表示PCER的收益率，图3蒙特卡罗模拟的价格走势。2.3MC算法的碳排放价格预测

令n=1000，根据Monte Carlo算法进行PCER价格预测的算法步骤进行预测，其价格预测的详细过程如表1所示。

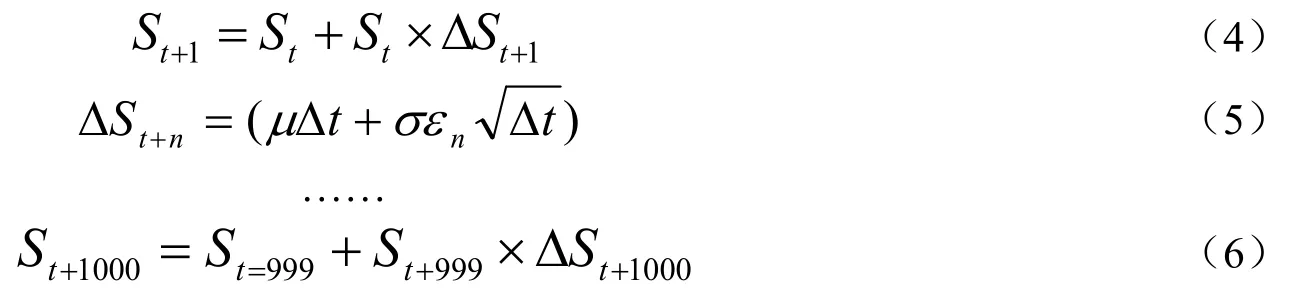
表1 PCER价格模拟过程表Table 1 PCER price simulation process

3 效果检验

3.1 Jarque-Bera检验

Jarque-Bera(JB)检验是一种检验正态分布的方法，其检验公式如下所示：

式（7）中，N为样本容量，S为偏度，K为峰度。

理论上，Monte Carlo算法模拟几何布朗运动所产生的价格数据序列服从对数正态分布。对数处理Monte Carlo算法模拟产生的碳排放价格数据，并进行JB统计量检验，检验结果如图4所示。由图4可知，当显著性水平为95%时，JB统计量的临界值是5.99，实际JB统计量为5.936369小于JB临界值，同时偏度S=-0.034840，非常接近于0，峰度K=3.096913，近似等于3，由JB检验结果可知，蒙特卡罗算法模拟产生的价格进行对数处理之后的数据服从正态分布的原假设。此外，通过JB检验可以从侧面反映出蒙特卡罗算法模拟价格过程的可靠性较高。

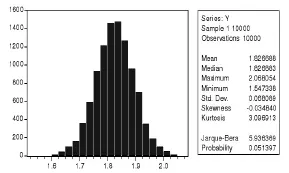
图4 模拟PCER价格对数的JB检验结果Fig.4 JB test results of simulated PCER logarithmic

3.2 计算VAR值

根据Monte Carlo算法模拟出来的碳排放价格数据序列，可以计算出VAR值。在置信水平c下，VAR的值由公式（8）可以计算获得。

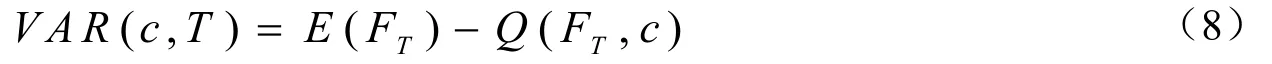
令n=1000，因此每一路径模拟次数都有1000步，即通过S1，S2，...，S1000预测F1000，一共模拟仿真1000次。如此重复1000次，产生1000个F1000。

当置信水平为99%时，由公式（8）可得：

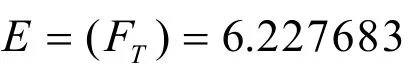
将模拟出的1000个价格进行升序排序，第100个数据为5.261681712，因此

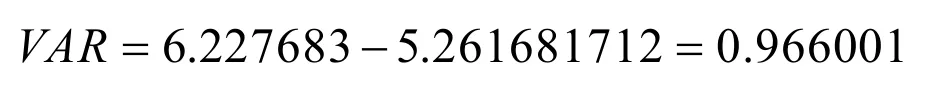
同理，当置信水平为95%时，VAR=6.227 683-5.555233=0.672451；当置信水平为90%时，VAR=6.227 683-5.696598=0.531085

通过上述分析研究发现，在正常市场状况下，当置信水平等于99%时，PCER价格下降会超0.966001只有1%的可能；当置信水平等于95%时，PCER价格下降会超过0.672451只有5%的可能；当置信水平等于90%时，PCER价格下降会超过0.531085只有10%的可能。

3.3 预测结果对比

为了验证本文算法的预测效果，将模拟价格和实际价格仿真对比，检验模型的预测效果，其预测效果如图5和图6所示。

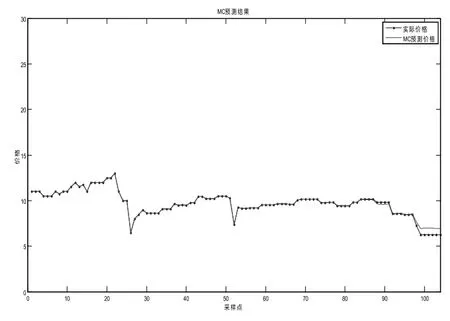
图5 MC预测效果图Fig.5 MC prediction effect

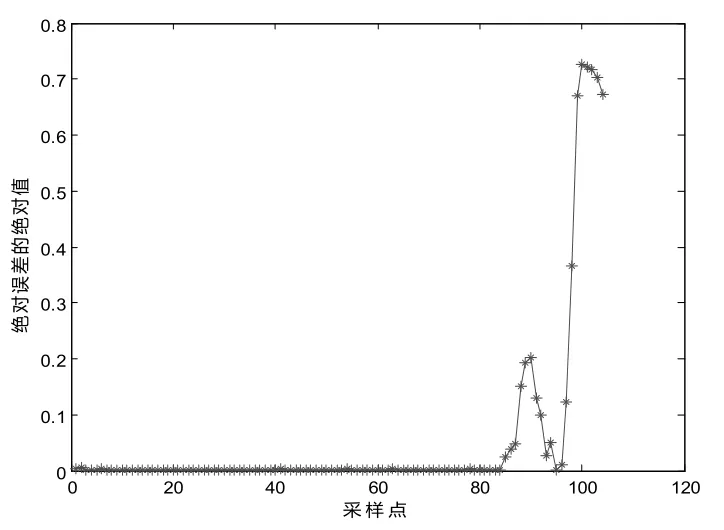
图6 MC预测误差图Fig.6 MC prediction error

由图5和图6 MC模拟结果图可知，MC算法可以很好的描述PCER价格的整体走势。通过MC模拟价格和实际价格的对比发现，将MC算法和几何布朗运动模型二者结合起来的预测模型可以有效预测，刻画价格走势的精度较高。

4 结论

针对几何布朗运动数学模型进行PCER价格预测存在的缺点，本文结合蒙特卡洛算法具有精度高、样本需求少的优点，将MC算法和几何布朗运动二者结合起来应用到PCER价格预测和收益分析，通过维纳过程表达的方式构建出数学模型，之后运用蒙特卡罗算法模拟维纳过程的变化规律，实现PCER价格的预测，通过JB统计量检验和VAR检验，仿真结果表明，本文算法具有预测精度高、数据样本要求少的优点，可以应用于其他经济规律的模拟仿真，为理论决策提供科学的依据。

[1]Alberola E,Chevallier J,Chèze B.Price drivers and structural breaks in European carbon prices 2005-2007[J].Energy Policy,2008,36(2):787-797

[2]Chevallier J.Carbon futures and macroeconomic risk factors:A view from the EUETS[J].Energy Economics,2009(31):614-625

[3]Benz E,Trück S.Modeling the price dynamics of CO2emission allowances[J].Energy Economics,2009,31(1):4-15

[4]Alberola E,Chevallier J,Chèze B.Emission Compliances and Carbon Prices under the EU ETS:A Country Specific Analysis of Industrial sectors[J].Journal of Policy Modeling,2009,31(3):446-462

[5]叶青.基于GARCH和半参数法的VaR模型及其在中国股市风险分析中的应用[J].统计研究,2000(12):25-29

[6]陈守东,王鲁非.上证综合指数VaR的度量[J].数量经济技术经济研究,2002(4):103-106

[7]田新时,刘汉中,李耀.沪深股市一般误差分布(GED)下的VaR计算[J].管理工程学报,2003,17(1):25-28

[8]曹志广,王安兴,杨军敏.股票收益率非正态性的蒙特卡罗模拟检验[J].财经研究,2005,31(10):34-41,52

[9]陈守东,俞世典.基于GARCH模型的VaR方法对中国股市的分析[J].吉林大学:社会科学学报,2002(4):11-17

[10]周浩,康建伟,陈建华,等.蒙特卡罗方法在电力市场短期金融风险评估中的应用[J].中国电机工程学报,2004,24(12):74-77

[11]陈磊山,姜冬梅,刘庆强,等.我国小型CDM项目开发障碍及其对策研究[J].环境保护科学,2008,34(6):45-47

[12]Manset-Bataller M,Chevallier J,Herve-Mignucci M,et al.EUA and sCER phase II price drivers:Unveiling the reason for the existence of the EUA-sCER spread[J].Energy Policy,2011(39):1056-1069

Application of the Improved Monte Carlo Algorithm in Prediction for Price of Carbon Emission Rate and Analysis on Earnings

LIU Da-xu
CentraI Branch of Weifang PeopIe's Bank of China,Weifang261000,China

In tradition,most of econometric methods are to be analyzed the carbon price prediction and earnings,but they have a high requirements for the truth and quantity of samples.Monte Carlo Algorithm takes advantage of the high prediction accuracy to suit for analyzing small samples in carbon emission prediction and earning analysis.This paper established the mathematical model based on Wiener motion equations and then combined Monte Carlo Algorithm to simulate the variation of the Wiener movement in order to achieve a carbon price prediction.The results of JB statistics and VAR test showed that improved Monte Carlo Algorithm had a higher prediction accuracy and more stronger in carbon price description and characterization.It was applied to provide a scientific basis for decision-making futures trading and price carbon emissions,it could be used to quantitatively describe and predict the rest of the economy and the direction.

Monte Carlo Algorithm;carbon emission;prediction

TP391.1

:A

:1000-2324(2015)06-0957-04

2014-08-20

:2014-10-25

刘大旭(1989-),男,山东省枣庄市人,本科,助理工程师.主要从事计算机科学技术研究.E-mail:liudaxu12315@163.com