数学史融入高等数学教学的探索与实践

李春丽， 穆 柯

(周口师范学院 数学与统计学院，河南 周口 466001)

数学史融入高等数学教学的探索与实践

李春丽， 穆 柯

(周口师范学院 数学与统计学院，河南 周口 466001)

数学史与数学教育的结合为高等数学教学改革提供了一个新的视角.阐述数学史融入高等数学教学的重要作用,分析数学史融入高等数学教学的内容材料的选择,探索数学史融入高等数学教学的方式,以具体教学案例展示数学史融入高等数学教学的实践做法.

数学史；高等数学；教学案例;极限；无穷级数

在高等数学教学中,笔者进行了如下的探索与尝试，更新教学内容,利用历史背景知识来激发学生学习高等数学的兴趣,为学生创造学习高等数学的动机;介绍数学概念和数学思想的形成与发展历程,帮助学生理解数学概念和数学思想;重现数学思想和方法的产生过程与情景,引导学生进行探究,提高学生发现问题、分析问题和解决问题的能力.

1 数学史融入高等数学教学的作用及内容材料的选择

早在19世纪，西方学者就意识到数学史对数学教育的作用.美国数学史家卡约黎(Cajor)提出，一门学科的历史知识,有助于使该学科更具吸引力,通过数学史的介绍,可以让学生体会到：数学并不枯燥呆板,而是一门不断发展的生动有趣的学科.英国数学史家福弗尔(Fauvel)总结了数学史融入数学教学的15种理由[1].在高等数学教学中合理地应用数学史,对学生来说,可以增加学习兴趣、获得数学学习的动机,可以加深对数学知识的理解和掌握,可以增强敢于质疑、敢于挑战的勇气和信心,可以领会数学的价值等;对教师来说,可以以史为鉴,有助于预见学生的学习困难,有助于合理安排课程内容顺序，有助于合理设计教学方式,为学生提供探究机会等.

数学史融入高等数学教学能有效地促进数学教学,但在数学史内容的选择上,应遵循科学性、实用性、趣味性原则，数学史内容必须是正确的,即不可随意编造,随意虚构,所选择的数学史料对学生数学学习和能力的提高要有直接帮助,所选的内容题材要有趣味性,以达到寓教于乐的目的.高等数学中,融入的数学史料可以是数学概念的形成和发展的故事,可以是数学对其他领域发展的促进和影响,也可以是数学家的贡献及生平简介,但重点应该是高等数学中数学思想、方法的形成、发展、完善的历程,如数学思想方法的形成背景及过程;数学家是如何发现问题,探索尝试并解决问题的;社会发展的需求是如何促进数学发展的等.在高等数学教学中应用数学史的主要目的是加强学生对教学内容的理解,对数学思想和方法本质的认识,让学生体会数学的作用和地位,激发学生的学习兴趣,提高学生发现问题、分析问题和解决问题的能力.

2 数学史融入高等数学教学的教学案例

数学史料融入高等数学教学的方式可以是多样化的，如讲述趣闻轶事可以增加课堂情趣;介绍数学悖论、数学家的错误可以培养学生勇于探索、敢于质疑的精神;介绍知识专题历史可以勾画知识发展概要;讲述数学家们创新的细节可以促进学生对方法的理解;重现数学知识的应用背景,可以提高学生应用数学知识去解决问题的意识等.下面是数学史融入高等数学教学的几个教学案例.

2.1 无穷级数的教学设计

美国数学史家与数学教育家克莱因认为:数学教学的关键是动机问题[2].历史上数学家进行数学创造时的动机是解决具体问题,鉴于此,可以利用数学史知识为学生提供数学学习的动机和兴趣.在进行无穷级数的教学时,可以用几个经典问题来引入无穷级数概念.

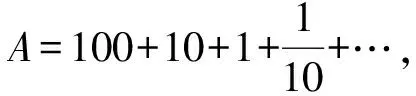
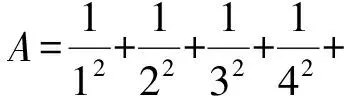
这样一来,无穷级数和无穷级数收敛性概念将不再是无本之木,无源之水,学生也将被这些历史难题深深吸引,这样数学学习的动机和兴趣就有了.

2.2 极限教学设计

在高等数学教学过程中,探索数学思想和方法的来源,揭示数学思想和方法的形成、发展过程,能帮助学生更好地理解和掌握这些思想和方法.

在教学过程中,为了更好地理解极限概念和掌握极限思想及其应用,可以对极限思想的产生和发展过程,从历史的角度进行详细的介绍.首先是极限思想的萌芽阶段,从希腊学者德谟克里特创立的“原子论”[2],到欧多克索斯创立的“穷竭法”,从《庄子·天下篇》中的“一尺之棰”[4]到3世纪刘徽的割圆术,以及祖冲之计算圆周率的问题中,都蕴含着最原始的朴素的极限思想.其次是极限理论的发展阶段,极限思想的进一步发展与微积分的建立紧密相连.17世纪牛顿和莱布尼茨利用实无穷小法创立了微积分,但由于对无限思想认识上的不足,在运算过程中出现了逻辑矛盾,牛顿意识到极限概念的重要性,并给出了极限的直观性定义,但这并没有解决这一矛盾,特别是贝克莱悖论的提出,使这一矛盾进一步激化,引起了数学史上的第二次数学危机,数学家们不得不考虑微积分理论基础的建构问题.再次是柯西给出定量化定义和维尔斯特拉斯给出符号表达的数学定义的阶段[5].

这样的专题历史介绍能让学生体会数学思想产生的实际背景和过程,使学生对极限思想的本质有了更深入的理解,同时能让学生体会数学家们敢于质疑、勇于挑战的精神[6].

2.3 常数变易法教学设计

在进行高等数学教学过程中,不仅应传授知识和方法,更应分析其产生的过程,应把教学过程当作学生参与的研究与探索过程,使学生不仅掌握前人的研究结果,又了解结果产生的过程,从而加深对知识和方法的理解,进而掌握科学的方法论.

常数变易法是求解非齐次线性微分方程的一种重要方法,它是数学家拉格朗日(Joseph Louis Lagrange)历经11年才得出的研究成果,但高等数学教材仅介绍了他的结论并没有展现探索过程.我们以常数变易法求解一阶线性微分方程为例,在教材中[7]一阶齐次线性微分方程

(1)

(2)

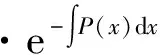
数学史不仅讲述数学悖论、数学难题,又能再现数学家的研究经历,还揭示数学思想和方法的形成、发展过程.在高等数学教学中,选择合适的数学史料融入教学过程,能有效地提高教学质量,但要真正发挥数学史在高等数学教学中的作用,关键在于数学史料的选择以及融入形式要适合于教学,不能脱离教学甚至是喧宾夺主.这就要求我们教师要掌握丰富的、系统的数学史知识,熟悉数学史与数学教育的关系,在此基础上设计出更好、更多的数学史融入高等数学教学的教学案例.

[1] 吴骏,汪晓勤.国外数学史融入数学教学研究述评[J].比较教育研究,2013,35(8):78-82.

[2] M·克莱因.古今数学思想:第一册[M].张理京,张锦言,江泽涵,译.上海:上海科学技术出版社,2003:211-213.

[3] 朱家生.数学史[M].2版.北京:高等教育出版社,2011：18-19.

[4] 张奠宙.关于数学史和数学文化[J].高等数学研究,2008,11(1):18-22.

[5] 邓纳姆.微积分的历程——从牛顿到勒贝格[M].李伯民,王军,张怀勇,译.北京:人民邮电出版社,2010:198-203.

[6] 汪晓勤.通识限选课程数学文化的教学实践[J].高等理科教育,2012(4):112-115.

[7] 同济大学数学系.高等数学 [M]. 6版.北京:高等教育出版社,2007:310-314.

Exploration and Practice on Using History of Mathematics in Higher Mathematics Teaching

LI Chunli, MU Ke

(SchoolofMathematicsandStatistics,ZhoukouNormalUniversity,Zhoukou466001,China)

The combination of history of mathematics and mathematics education provides a new perspective for the reform of higher mathematics teaching. First, the teaching role of using history of mathematics in higher mathematics teaching was explained, and then the methods of using history of mathematics in higher mathematics teaching were analyzed. Finally, a few teaching cases of using history of mathematics in higher mathematics teaching were demonstrated.

history of mathematics; higher mathematics; teaching case; limit; infinite series

2015-06-19

河南省教育厅教师教育课程改革研究项目(2013-JSJYYB-080)

李春丽(1983—),女,河南淮阳人,周口师范学院数学与统计学院讲师.

10.3969/j.issn.1007-0834.2015.04.019

G642

A

1007-0834(2015)04-0068-03