一种改进预条件的AOR迭代法收敛性的讨论

李星星， 朱星华

(1.郑州城市职业学院 基础部,河南 郑州 452370;2.南方科技大学 基础部,广东 深圳 518055)

一种改进预条件的AOR迭代法收敛性的讨论

李星星1， 朱星华2

(1.郑州城市职业学院 基础部,河南 郑州 452370;2.南方科技大学 基础部,广东 深圳 518055)

提出了一种改进预条件的AOR迭代法，并证明了在非奇异M-矩阵下,该改进预条件加速了AOR迭代法的收敛性．通过理论分析和数值实验验证，该方法均优于文献中所提出的预条件方法(I+S)．

L-矩阵；非奇异M-矩阵；预条件；收敛性；AOR迭代法

0 引言

求解线性方程组是数值线性代数的一个基本问题，即给定A∈Cn×n,b∈Cm，寻找解向量x∈Cn使得

Ax=b.

(1)

求此线性方程组所使用的传统方法是Gaussian消元法，即假设系数矩阵A是一个n×n的非退化阵，它的运算量是O(n3)．现在一般研究的是用迭代法求方程组(1)的近似解，即用某种极限过程去逐渐逼近精确解，并发展了许多非常有效的迭代方法，常见的迭代法包含了Jacobi、Gauss-Seidel、SOR(succesive over relaxation)和SSOR(symmetric successive over relaxation)等方法，其中Jacobi和Gauss-Seidel迭代法是比较简单的迭代法．近年来，为加速迭代法的收敛性，许多学者已采用预条件加速迭代法，甚至对一些不收敛的迭代法通过预条件处理后也可使得迭代法收敛．

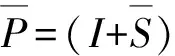
其中I是单位矩阵，an1分别是系数矩阵A=(aij)n×n对应位置上的元素，α、β都是正实数．

对线性方程组(1)，设A=D-E-F为非奇异矩阵(当A为奇异矩阵时，可通过矩阵变换为低阶的非奇异矩阵)，D为对角矩阵，E为严格下三角矩阵，F为严格上三角矩阵．结合矩阵的变换，A=D-E-F总可以变为A=I-L-U，其中I为对角矩阵，L为严格下三角矩阵，U为严格上三角矩阵．故只就A=I-L-U进行讨论．

求解方程组的AOR迭代法为x(m+1)=Tγ,ωx(m)+ω(I-γL)-1D-1b,m=1,2,….相应的迭代矩阵为Tγ,ω=(I-γL)-1[(1-ω)I+(ω-γ)L+ωU]，在预条件P=(I+S)后，方程组(1)变为

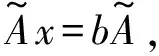
(2)

而相应的系数矩阵变为

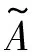
(3)

类似地，有

(4)

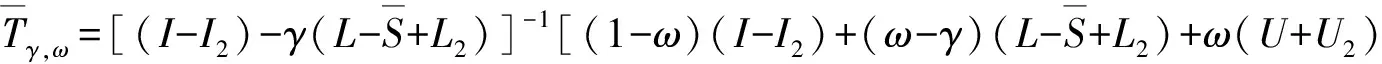
1 预备知识

定义1[2]若M是非奇异n阶方阵，则称A=M-N是A的分裂；若ρ(M-1N)<1，则称分裂A=M-N是收敛的；若M-1≥0，N≥0则称分裂是正规的；若M-1≥0，M-1N≥0，则称分裂A=M-N是弱正规的；若M是非奇异的M-矩阵，且N≥0，则称分裂A=M-N是M-分裂；若M-1N≥0，则称分裂A=M-N是弱非负的．

引理1[3]设A=(aij)∈Zn×n为非奇异M-矩阵，且D∈Zn×n满足D≥A，那么就有A-1与D-1都存在，并且还有A-1≥D-1≥0．

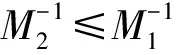
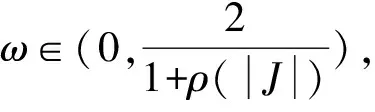
引理4[6]设A=M1-N1=M2-N2是A的两个弱正规分裂，且若满足下列条件之一：①N1≤N2；②N1≥0；③N2≥0，则ρ(M1-1N1)≤ρ(M2-1N2)<1.

2 主要结果及证明

在文献[1]中，经过预条件P=(I+S)后的迭代矩阵为

那么有以下结论：

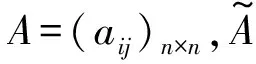
证明 由于

则L1≥0,I1≥0，U1=0．

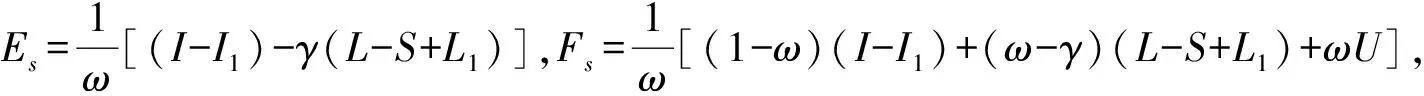
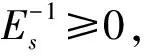
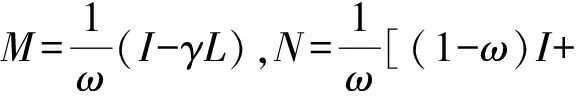
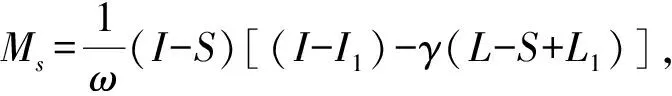
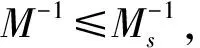
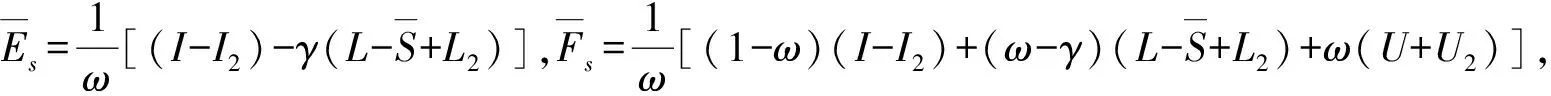
而

因为βan1+α≤0，故I2≥0，L2≥0，U2=0．由于(β-1)an1+α≥0，易知

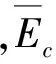
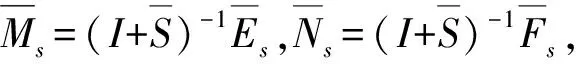
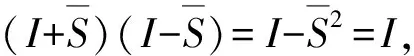
从而

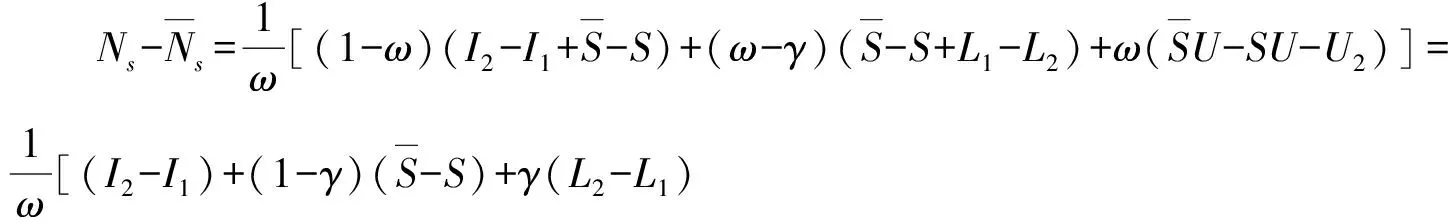
又,

综上所述，有

3 数值实验

例1 设线性方程组(1)的系数矩阵为

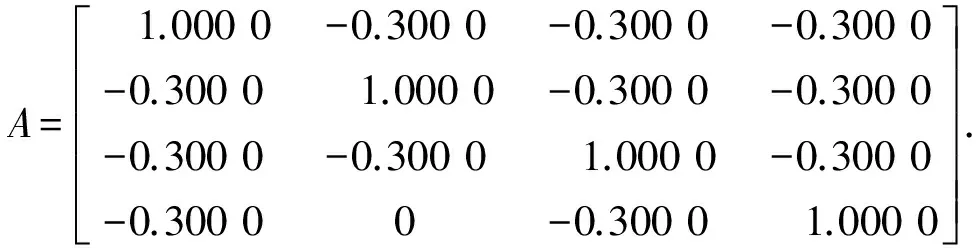
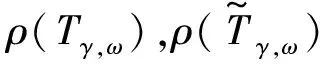
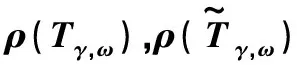
表1 α 和β 取不同的值时和的大小比较

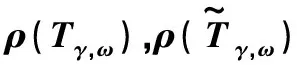
表2 ω 和γ 不变的情况下和的大小比较

实验表明，在满足定理的条件下，对α和β取不同的值时，本文的预条件后收敛速度较快,且α和β越小，对比越明显，即预条件后的收敛速度更快.

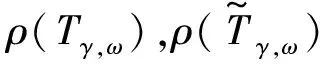
3.2 比较α和β取不同的值时预条件AOR迭代法迭代矩阵谱半径的变化规律

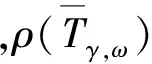
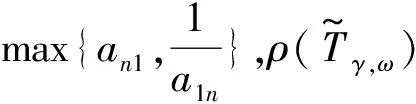
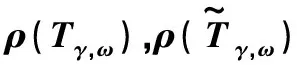
表3 α 和β 取不同的值时和的大小比较

4 小结

笔者提出的预条件迭代矩阵的谱半径要比文献[1]中提出的预条件迭代矩阵谱半径小，在一定程度上改进了迭代法的收敛速度．特别地，存在一些不满足定理条件的参数，当取这些参数时，预条件迭代矩阵的谱半径仍比文献中的预条件迭代矩阵谱半径小.

[1] LI YAOTANG,WANG ZHUANDE.A modified AOR iterative method for preconditioned linear systems[J].Southeast Asian Bulletin of Mathematics,2004,28(2):305-306.

[2] RICHARD S V.Matrix Iterative Analysis[M].Heidelberg:Spring-Verlag,2000:87-94.

[3] DAVID M Y.Iterative Solution of Large Linear Systems[M].New York: Academic Press,1971:59-61.

[4] 张谋成,黎稳.非负矩阵论[M].广州:广东高等教育出版社,1995：43-76.

[5] 戴华.矩阵论[M].北京:科学出版社,2001:283-284.

[6] ELSNER L. Comparisons of weak regular splittings and multisplitting methods[J].Number Math,1989,56:283-289.

Discussion on Convergence of an Improved Preconditioned AOR Iterative Method

LI Xingxing1, ZHU Xinghua2

(1.DepartmentofBasic,CityCareerAcademyofZhengzhou,Zhengzhou452370,China;2.DepartmentofBasic,SouthUniversityofScienceandTechnologyofChina,Shenzhen518055,China)

An improved preconditioned AOR iterative method is presented. It proves that the improved precondition, in the condition of a nonsingularM-matrix, accelerates the convergence of AOR iterative method. According to the theoretical analysis and numerical experiments, the proposed method is prior to the method in document (I+S).

L-matrix; nonsingularM-matrix; preconditions; convergence; AOR method

2015-05-20

李星星(1987—)，女，山西文水人，郑州城市职业学院基础部教师.

10.3969/j.issn.1007-0834.2015.04.007

O241

A

1007-0834(2015)04-0024-05