有理Bézier曲线形状修改的研究
2015-03-24李迎娣
李迎娣
(黄河科技学院 国际学院,河南 郑州 450000)
有理Bézier曲线形状修改的研究
李迎娣
(黄河科技学院 国际学院,河南 郑州 450000)
研究关于修改有理贝齐尔(Bézier)曲线的方法.通过控制点、权因子的单个及多个修改改变有理贝齐尔曲线的形状,在此基础上附加限制条件达到对有理贝齐尔曲线的精确修改.
有理贝齐尔曲线;控制顶点;约束最优化;导矢;权因子
1 有理Bézier曲线介绍[1-2]
法国雷诺公司的贝齐尔(Bézier)在1971年构思了一种构成曲线的方法,即可以由控制多边形来定义.设计员通过控制顶点的移动就可以进行曲线形状的修改,并且曲线形状的变化可以在控制之中.Bézier方法方便简单,易于掌握,还可以较好地进行几何产品造型的整体形状的控制.Bézier方法在CAGD(Computer Aided Geometric Design)中有重要的作用和地位,它很容易被人们所理解接受.但是Bézier方法仍有着连接的问题,而且还存在着局部修改的问题. Bézier方法不具有局部的性质,即控制多边形的任一个顶点的改变都会影响整张的曲面或者整条曲线的形状.有时曲面、曲线的形状会很复杂,这时需要的是增加控制多边形顶点的个数,以使曲面、曲线的幂的次数增高.有时曲线的幂的次数很高, Bézier曲面或者曲线的形状会与控制多边形(定义该曲面或者曲线)有着很大的差距.之后,就有很多学者研究怎样通过修改Bézier曲线克服这些缺点.例如:沿着固定方向的有理Bézier曲线形状的定量修改;沿着任意方向有理Bézier曲线形状的定量修改;增加控制顶点的修改方法.本文研究的是通过修改有理Bézier曲线上的权因子或控制顶点,修改n次有理Bézier曲线的形状.然而在现实的工作中,更多的是进行有要求或有目的性的修改,比如,使得修改后的有理Bézier曲线过某指定点.
n次有理Bézier曲线方程的有理表达式为
(1)
其中,Bi,n(t)是Bernstin基函数,即
其中,wi(i=0,1,…,n)是权因子,wi(i=0,1,…,n)分别与相应的控制点bi(i=0,1,…,n)相对应.权因子w0>0,wn>0,wi≥0,为了不让分母为零,顺序k个权因子是不同时为零的.bi(i=0,1,…,n)是控制点, 控制多边形由折线b0,b1,…,bn构成.

2 有理Bézier曲线的形状修改[3]
R(t)是参数为t的有理Bézier曲线,点T是已知的目标点,S是已知曲线上的点,现在的目标是让修改后的曲线R′(t)过该点,故需要研究的是:如何在满足原Bézier曲线形状改变最小的情况下,达到该目标.
定义有理n次Bézier曲线的方程为
其中,Bi,n(t)是第i个n次Bernstin基函数.现实问题中有理二次、三次、四次Bézier曲线用得较多.
2.1 通过修改单个控制顶点来改变n次有理Bézier曲线的形状
假设需要修改的控制顶点是dj,εj是控制顶点dj的相应扰动量,则得到的有理n次Bézier曲线是
由条件知,修改后的Bézier曲线通过目标点T,得
(2)
2.2 修改单个权因子改变n次有理Bézier曲线的形状
假设要修改的权因子wj,δj是权因子wj的相应扰动量,则得到的有理n次Bézier曲线
(3)
(1)式、(2)式分别改变单个控制点和权因子,对有理n次Bézier曲线的形状进行有目的的修改.
下面讨论同时改变单个控制点和权因子时,n次有理Bézier曲线形状的改变.
2.3 同时改变单个控制顶点和权因子来修改n次有理Bézier曲线的形状
假设需要修改的权因子是wj,相应的控制点是dj,则修改后的Bézier曲线是
(4)

3 保持导矢方向不变来改变有理Bézier曲线的形状
R(t)是参数为t的有理Bézier曲线,点T是已知的目标点,S是已知的曲线上的点,现在的目标是使修改后的曲线R′(t)过该点且在该点处的导矢方向与S点处的导矢方向相同,所以我们研究的是:在满足原Bézier曲线形状改变最小的情况下,如何达到新的目标.
3.1 修改多个控制顶点且保持导矢[4]方向不变修改有理Bézier曲线的形状
假设需要修改的控制顶点为dj(j=i1,i2,…ir),相应的扰动量为εj(j=i1,i2,…ir),
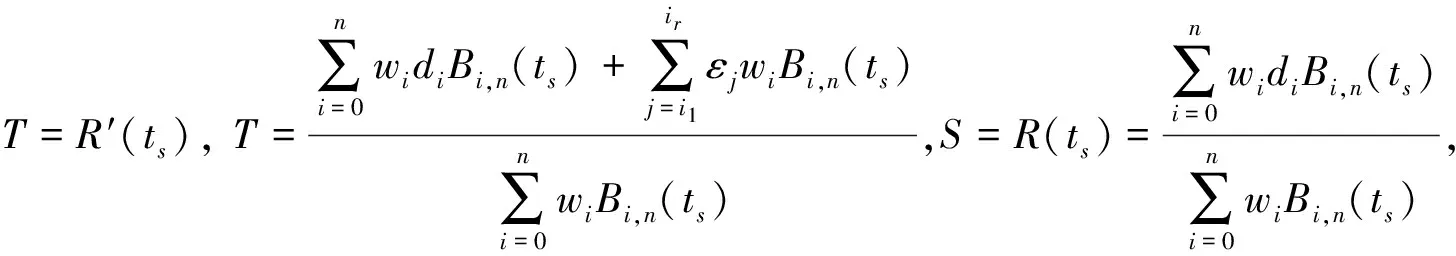
由条件Bézier曲线在目标点处的导矢方向保持不变,故有

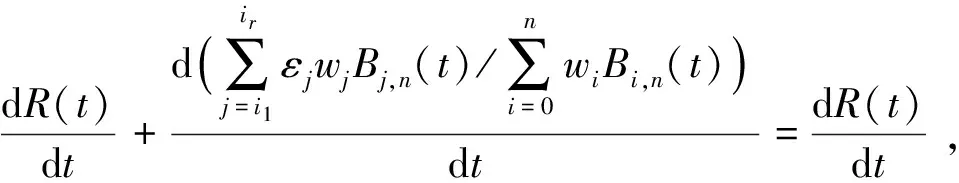
故
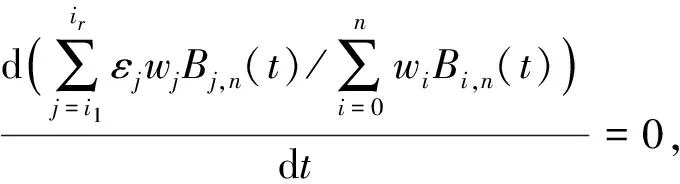
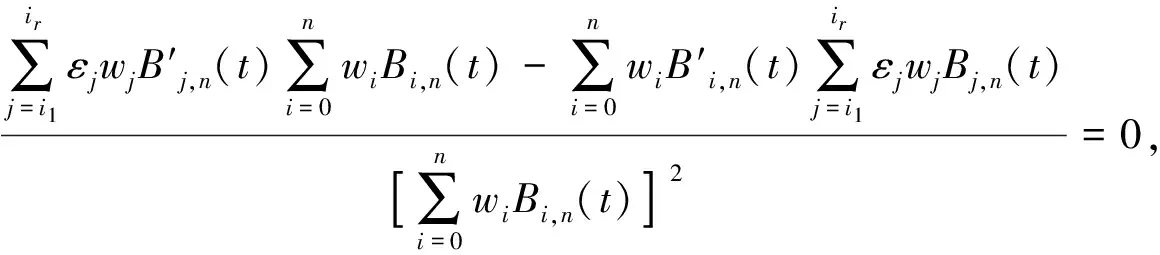
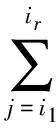
其中τ,λ为Lagrange算子,故依据约束问题的Lagrange法,得到
于是得到以下方程组,
解之,可得符合条件的εj值.
3.2 修改多个控制顶点且保持导矢[4]方向不变时修改有理Bézier曲线的形状
假设修改的权因子是wj(j=i1,i2,…,ir),相应的扰动量是δj(j=i1,i2,…,i),得到符合条件的曲线是

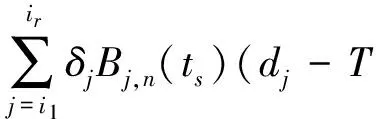
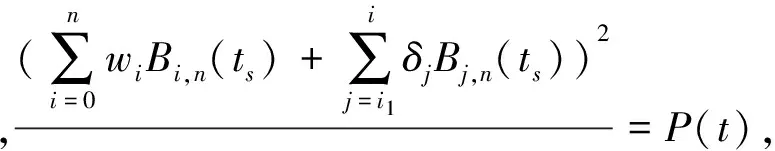

解之,可得δj的值.
[1] 王国瑾,汪国昭,郑建民.计算机辅助几何设计[M].北京:高等教育出版社,2001:35-43.
[2] 刘鼎元.有理Bézier曲线[J].应用数学学报,1985,8(1):70-83.
[3] 康宝生.有理Bézier曲线的可控修形[J].工程图学学报,1991(1):23-29.
[4] 陶诏灵.有理Bézier曲线导矢量法[J].气象教育与科技,2000(2):30-33.
[5] 韩旭里,任叶庆.基于位矢和切矢约束优化的Bezier曲线形状修改[J].计算机辅助设计与图形学学报,2008,20(9):1 191-1 195.
Study on Modification of Rational Bézier Curve Shape
LI Yingdi
(InstituteofInternationalStudy,HuangheScienceandTechnologyCollege,Zhengzhou464000,China)
The change of method about rational Bézier curve is studied. First, through the change of single control point, right factor and the simultaneous, the shape of rational Bézier curve is changed. Second, restrictive condition is added to change the shape of rational Bézier curve.
rational Bézier curve; control point; optimization constraint; derivative; right factor
2015-05-11
李迎娣(1985—),女,河南商丘人,黄河科技学院国际学院教师.
10.3969/j.issn.1007-0834.2015.04.005
O110
A
1007-0834(2015)04-0016-05
