一种提高CAPS导航通信融合系统保密性的新方法*

何瑞珠，胡正群，崔君霞，裴 军

(1. 中国科学院国家天文台，北京 100012；2. 中国科学院大学，北京 100049)

一种提高CAPS导航通信融合系统保密性的新方法*

何瑞珠1,2，胡正群1，崔君霞1，裴 军1

(1. 中国科学院国家天文台，北京 100012；2. 中国科学院大学，北京 100049)

根据导航通信融合系统的特点，通过伪随机序列码与混沌序列码的复合得到GC(Gold-Chebyshev)序列码，新序列码克服了混沌序列平衡性差的缺点，满足了系统短码的要求，得到的GC序列具有码组数量几乎无限多和序列线性复杂度好的优点。系统以伪随机跳变的方式更换码序列集合，极大地提升了系统的安全性。对换码模式和系统性能进行实验验证，表明复合新码GC序列采用换码模式易于实现可靠通信，还可以有效提高系统的保密性能。

导航通信；保密通信；换码；导航通信融合系统

在卫星通信系统和卫星导航系统迅速发展的今天，将两者结合在一起建立导航通信融合系统已成为一种发展趋势[1-2]。2002年11月，中国科学院国家天文台等相关单位的专家，利用在天文学研究中长期积累的信号被动接收和微弱信号检测、卫星动力学研究和卫星测轨定轨、时间溯源比对等方面的优势，组成卫星导航科研项目组，发明了主要基于商用通信卫星的能够实现导航通信一体化的中国区域定位系统(Chinese Area Positioning System, CAPS)。导航通信系统不仅能满足人们日常生产生活的民用需求，还广泛应用于国家安全领域，因此对系统的保密性要求越来越高。随着技术的发展，依靠传统PN码对信号进行扩频的传统保密方式已经不能满足高保密性的要求[3-4]，而且现有的绝大部分提高系统保密性的方法，几乎都是单独针对导航定位系统和通信系统的[5-7]，对于在信号结构上将两者一体化的导航通信融合系统来说，这些方法并不完全适用。针对系统特殊信号结构和大用户容量的需求，需要对保密性进行深入研究，并对扩频码进行新颖设计。本文提出了提高导航通信融合系统保密性的一种新方法，根据导航通信信号融合系统信号结构的特点，以及目前传统伪随机码和典型混沌序列应用于这类系统时可能存在的不足，构造复合序列，优选提供数量众多性能优良的码序列集合，使系统能够以伪随机跳变的方式更换使用的码组集合。同时新序列良好的线性复杂度为系统的保密性提供了第二重保障。

1 导航通信融合系统保密性能要求

为了提高接收机捕获性能，在导航通信融合系统中通常采用I/Q正交调制的通信体制，在信号结构上将导航电文和通信电文融合成一体，使其既满足通信系统对信号的要求，同时也满足导航系统对信号的要求。信号结构原理如图1。

在现有的导航定位系统中，大都使用传统的伪随机序列。以广泛使用的Gold码为例进行分析，这类伪随机码在抗干扰等方面性能优良，但是码组数量有限，不能满足导航通信系统对用户容量需求的增多[7-8]，而且传统的PN序列的线性复杂度决定其保密性能差，该类码也不能适用换码系统。

混沌序列的码组数量多，但是平衡性不好，当序列长度较短时，平衡度大于0.02，此时混沌序列的平衡性不能满足通信系统的要求[9-11]。在导航通信融合系统中，为了能快速捕获，经常需要短码

进行引导，这样混沌序列并不能使用。

系统的保密性与扩频码的性能具有直接关系。如果系统使用的扩频码自身的保密性能好，同时有充足的码组数量可以满足系统不断更换码组集合的要求，那么系统的保密性将大大提高。

为了实现使用换码功能提高导航通信融合系统的保密性，需要构造码组充足、平衡性和保密性优良，同时又能实现可靠通信的新码组。

2 换码方法实现

2.1 构造新型Gold-Chebyshev序列

传统的伪随机码序列和混沌序列各有优缺点，其中任何一种都不能满足导航通信融合系统对高保密性的要求。Chebyshev混沌序列是一种一维混沌映射，其迭代方程如(1)式，易于实现。ω阶Chebyshev映射的定义为

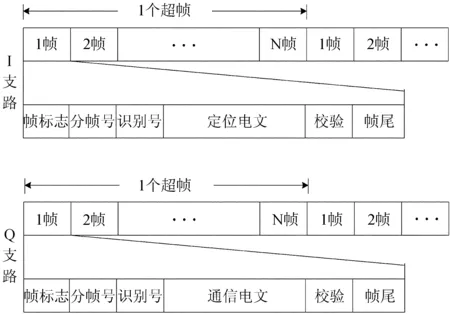
图1 导航通信融合的信号结构

Fig.1 Illustration of the structures of signal strings of an integrated system of navigation and communication

(1)

(1)式中，当ω≥2时，系统处于混沌状态，并且具有各态历经性和正交性，不同的初始值经多次迭代后的序列一定互不相关。一般取ω=2n，n表示任意整数。

Gold序列是典型的常用的传统扩频序列，具有优良的平衡性，但是保密性不好。 Chebyshev序列与Gold序列复合得到Gold-Chebyshev(GC)序列，不仅具有传统扩频序列良好平衡性的优点，而且在保密性上具有优于传统扩频序列的特点，GC复合序列的复合形成原理如图2。

图2 GC序列复合方式原理框图
Fig.2 A block diagram showing the construction of a GC sequence

利用混沌模型产生Chebyshev序列，由混沌系统迭代产生的混沌信号是状态连续的模拟信号，要将其应用于数字扩频通信系统中，必须首先将实值模拟混沌信号二值量化，得到二值(0, 1)或(1, -1)数字序列。该方法中Chebyshev序列和Gold序列均为(1, -1)序列，从中可以优选自相关和互相关性能好的新复合序列。

2.2 GC码的保密性能验证

2.2.1 GC码的码组数量

由Gold-Chebyshev序列复合原理可知复合后产生的新序列——GC序列随着引入的混沌初始值和分形参数的改变可以产生无限多的码序列，图3是迭代轨迹和量化后的二值序列随迭代次数的变化，当初始值为0.65和0.650 01时，只有0.000 01的变化，但是迭代结果明显不同，产生完全不一样的序列。这样的特性使得系统的通信容量不再受到扩频码数量的限制，保证了系统以随机跳变的方式更换码组集合的可行性。

2.2.2 GC码的平衡性分析

充足的码组数量是换码系统的必要条件，但是码组本身的其他性质对提高保密性也至关重要。序列的平衡性直接影响系统的保密性能，平衡性与载波抑制度有着密切的关系，不平衡码会使扩频系统载波泄漏增大，破坏扩频系统的保密性、抗干扰能力和抗侦破能力，并且会增加接收机内部干扰，影响接收质量。采用平衡度来衡量平衡性，平衡度为0表示序列的平衡性非常好。

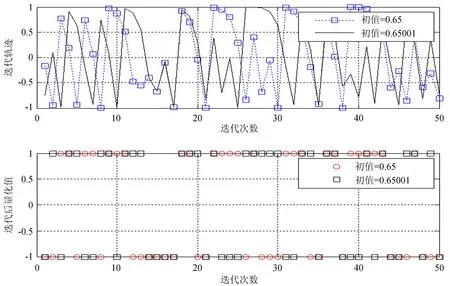
图3 迭代轨迹和序列随迭代次数的变化
Fig.3 The changes of trajectories and sequences along with the number of iterations

导航通信融合系统是一个需要大量短码调制导航信息以实现快速捕获的系统，几种常用的混沌序列平衡度如图4，在序列长度较短的范围内，大量的序列平衡度E大于0.02，不能满足通信系统的要求。GC序列的平衡度如图5。

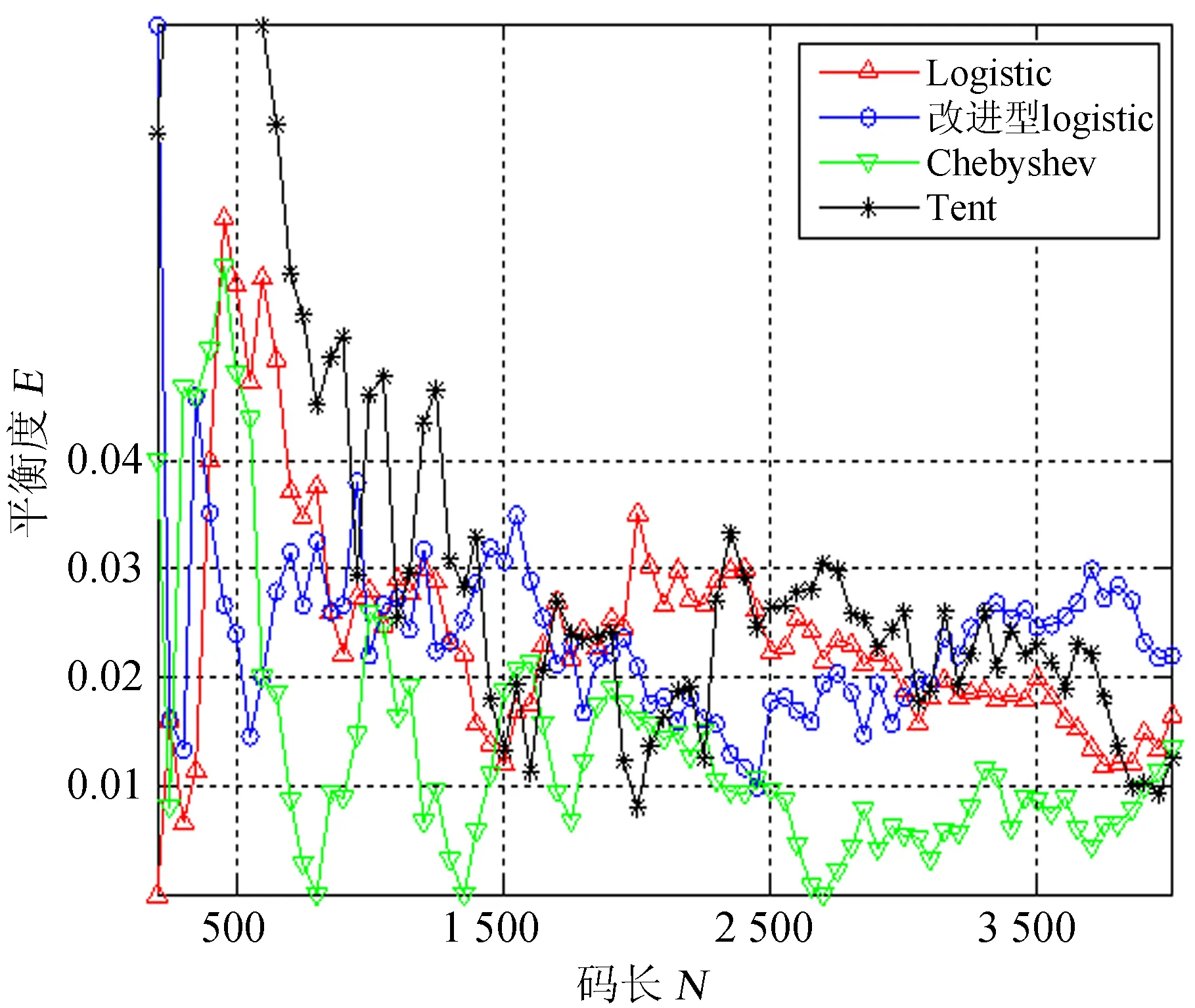
图4 几种常用混沌序列的平衡性

Fig.4 The levels of balance of several commonly used types of chaotic sequence

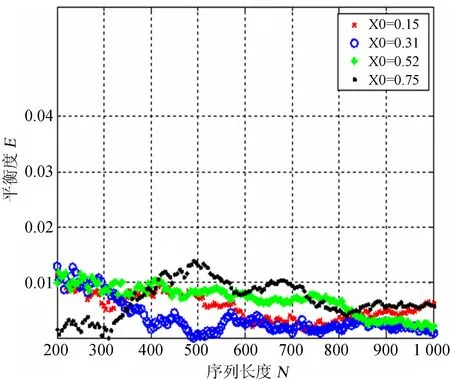
图5 GC序列的平衡性

Fig.5 The levels of balance of representative Gold-Chebyshev sequences

由图4和图5可知，GC序列克服了混沌序列平衡性不如传统PN序列的缺点，即使是在序列长度较短时都有良好的平衡性能，GC序列可以给导航通信融合系统提供性能优良、数量众多的短码调制导航电文，实现快速捕获。

2.2.3 Gold-Chebyshev码的线性复杂度

线性复杂度是序列安全的重要指标，如果系统对抗干扰、抗截获性能要求比较高，那么扩频序列就必须要求较高的线性复杂度，因为线性复杂度的大小直接关系到整个系统保密性的好坏。

对于m序列，其线性复杂度就是产生该序列的移位寄存器的阶数n，同样长度的Gold序列的线性复杂度为2n。假设n=100阶移位寄存器m序列长度为N=2100-1，约1030长，但是仅用2×100-1=199个码元就可以破译此m序列。m序列之所以这么容易破译就是因为它的线性复杂度太小。序列的线性复杂度直接决定了扩频系统的保密性能，是扩频序列的主要指标之一。

对于长度为N序列，当线性复杂度为N/2时最好，过大或过小都不安全。Berlekamp-Massey算法是一种计算任意长有限序列的线性复杂度的有效方法，图6是使用Berlekamp-Massey算法得到的GC序列的线性复杂度与序列长度的关系图。

图6 Gold-Chebyshev序列短码线性复杂度
Fig.6 The linear complexity of Gold-Chebyshev sequences

由图6可知，新序列的线性复杂度是序列长度的一半，从而在安全性和保密性方面得到很大程度的提高。

3 系统性能验证

本实验验证主要通过构建基于相关接收的多用户通信系统，研究GC码在系统中的应用性能以及验证换码系统在有多址干扰和噪声干扰环境下的通信能力。实验系统原理框图如图7，主要包括扩频、调制、解扩、相关运算和判决等环节。实验系统平台通过MATLAB/Simulink搭建实现，如图8。

图7 实验系统原理框图
Fig.7 A block diagram of our experimental system

在图8中，user2到user10发送系统子系统结构和user1类似， receiver2到receiver10分别对应用户的接收端。换码码集合的生成方式如图9。

扩频码长取1 024，在相同实验条件下，添加用户数至50，分别使用Gold码和换码系统在有多址干扰和噪声干扰环境下进行实验，信噪比Es/E0取-30至-10 dB，多址干扰和噪声干扰环境下的误码率曲线如图10。

图8 多用户码分多址通信系统仿真模型
Fig.8 A block diagram illustrating our simulated multiple-user communication system using signal split

图9 换码备选码集合生成框图
Fig.9 A block diagram illustrating the generation of a pool of code sets for use in code switching

由图10可知，在各种信噪比的条件下，使用GC码的换码系统的性能跟抗干扰性能非常突出的Gold码一样优良。其信号的截获概率远远小于普通系统，非常适合导航通信融合系统。

4 结 论

本文设计并实现了一种提高导航通信融合系统保密性的新方法，构造新型的复合GC序列，在保证序列的性能满足系统正常进行导航通信要求的同时，可以进一步提高系统的保密性。这种保密性能的改善一方面体现在序列自身线性复杂度的最优化上，另一方面体现在充足的码组数量可以给系统提供多套备选码组以实现换码。方法易于实现，为保密通信和导航通信融合系统等对保密性要求较高的系统提供了一种有效的保密方式，在相关领域具有重要的参考价值。

图10 多址干扰和噪声干扰环境下的误码率曲线

Fig.10 The relation between the bit-error rate and the signal-to-noise ratio for our system

[1] Cui J X, Shi H L, Chen J B, et al. The transmission link of CAPS navigation and communication system[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2009, 52(3): 402-411.

[2] 艾国祥, 施浒立, 吴海涛, 等. 基于通信卫星的定位系统原理[J]. 中国科学 (G辑: 物理学 力学 天文学), 2008, 38(12): 1615-1633. Ai G X, Shi H L, Wu H T, et al. Positioning system based on communication satellites[J]. Science in China (Series G:Physics, Mechanics & Astronomy), 2008, 38(12): 1615-1633.

[3] Ai G X, Shi H L, Wu H T, et al. A positioning system based on communication satellites and the Chinese Area Positioning System (CAPS) [J]. Chinese Journal of Astronomy and Astrophysics, 2008, 8(6): 611-635.

[4] 曾兴雯. 扩展频谱通信及其多址技术[ M] . 西安: 西安电子科技大学出版社, 2004.

[5] 谭述森. 卫星导航定位工程[M]. 第二版. 北京: 国防工业出版社, 2010.

[6] 贺利芳, 张刚, 张天骐. 一种保密通信系统的研究[J]. 电信科学, 2012, 28(2): 99-103. He Lifang, Zhang Gang, Zhang Tianqi. Research on a security communication scheme[J]. Telecommunications Science, 2012, 28(2): 99-103.

[7] 尚俊娜, 施浒立, 卢晓春, 等. 基于时间位置和状态信息的导航通信一体化系统: 中国, 200610012056.4[P]. 2006-05-31.

[8] 陈振国, 杨泓文, 郭文彬. 卫星通信系统与技术[M]. 北京: 北京邮电大学出版社, 2003.

[9] 崔力, 欧青立, 张红强, 等. 混沌保密通信技术发展研究[J]. 通信技术, 2010, 43(5): 121-123. Cui Li, Ou Qingli, Zhang Hongqiang, et al. Study on chaotic secure communication development [J]. Communications Technology, 2010, 43(5): 121-123.

[10]Wang B, Wen G J. On the synchronization of uncertain master-slave chaotic systems with disturbance[J]. Chaos, Solitons and Fractals, 2009, 41(1): 145-151.

[11]Wang B, Wen G J, X K. On the synchronization of a hyperchaotic system based on adaptive method[J]. Physics Letters A, 2008, 372(17): 3015-3020.

CN 53-1189/P ISSN 1672-7673

A Novel Method to Enhance Communication Security in the CAPS Integrated System of Navigation and Communication

He Ruizhu1,2, Hu Zhengqun1, Cui Junxia1, Pei Jun1

(1. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China; 2. University of Chinese Academy of Sciences, Beijing 100049, China, Email: heruizhu11@mails.ucas.ac.cn)

In this paper we propose a novel method based on highly randomly switching code sets to enhance communication security of an integrated system of navigation and communication. A Gold-Chebyshev (GC) sequence constructed in our novel approach can overcome the shortcoming of poor balance performance of a conventional chaotic sequence, by preserving the main advantages of the latter, which are the large code number and high confidentiality. Our proposed secure system can randomly select a code set from a pool of GC code sets. This greatly improves the system security performance. We have also carried out simulations of operations of the system using the MATLAB/Simulink. Our simulations verify the feasibility of applying the novel method in an integrated system of navigation and communication.

Navigation and communication; Secure communication; Switching code sets; Integrated system of navigation and communication

国家自然科学基金 (61001109) 资助.

2014-03-04；修定日期：2014-03-18

何瑞珠，女，硕士. 研究方向：卫星导航与通信. Email: heruizhu11@mails.ucas.ac.cn

TN927

A

1672-7673(2015)01-0030-06