对流层波导中电波传播的抛物方程法及误差分析

杨明珊，邱志勇，杜晓燕

(1.郑州大学 信息工程学院, 河南 郑州 450001; 2.信息工程大学, 河南 郑州 450001)

对流层波导中电波传播的抛物方程法及误差分析

杨明珊1，邱志勇1，杜晓燕2

(1.郑州大学 信息工程学院, 河南 郑州 450001; 2.信息工程大学, 河南 郑州 450001)

对窄角抛物方程推导过程中引入的主要误差进行分析，建立近似过程产生的误差与传播仰角、大气折射指数变化的关系，关系式明确了两因子引入误差的大小与方程适用范围.并验证在对流层大气折射指数变化与较小传播仰角情况下，窄角抛物方程求解的可靠性.最后，运用该算法分别计算标准大气、蒸发波导与表面波导中电磁波传播的损耗值.

对流层波导；抛物方程算法；传播损耗；误差

0 引言

我国东南沿海处于对流层波导高发生地区，海岸及舰船上运作的雷达系统，通信和侦察等无线设备通常都会受其影响[1].例如，会使雷达产生传播盲区、杂波增强等；对通信系统也会产生相当大的干扰，严重时会导致通信中断.因此，针对对流层波导环境中电磁波传播特性研究的必要性日趋显现；此外，开展波导中电波传播研究还关系到战场环境中电磁压制和反压制、电波传播环境的利用和反利用等问题，具有重大国防和军事价值.

抛物方程算法是在1987年，由Dockery首次将其运用到对流层电波传播问题中[2]；二十世纪以来，美国海军研究小组一直致力于抛物方程模型的应用研究，并完成了基于离散混合傅里叶变换等方法的混合传输模型的技术报告[3].而我国对抛物方程法的研究却起步较晚且多数集中在水声领域，最近几年才逐渐在电磁计算领域得到关注.总体说来，目前国内计算电磁学领域对抛物方程法的研究还处于基础理论研究阶段.笔者首先由波动方程导出窄角抛物方程，并针对该推导过程引入的近似量进行分析，建立误差与传播仰角等因子的关系式，最后仿真分析了波导中电磁波传播损耗分布情况.

1 波导折射率模型

电磁波传播过程中，当传播距离较近时，可以近似认为地表面为平面；若传播距离大于极限直视距离，就必须探讨地球曲率的影响.为了解决这个问题，可以使用球面分层介质中的斯奈尔定律得到大气修正折射指数[4]

式中：z为海平面以上高度；n(z)为高度z处的大气折射指数；ae为地球半径，修正折射指数已经将地球曲率的影响考虑在内.进而，可得大气的修正折射率

(2)

标准大气的折射率梯度变化为定值，其折射率剖面为斜直线；而蒸发波导是由于海面水汽蒸发使得海面上空较小高度范围内的大气湿度急剧减小而形成的，其修正折射率数学模型可表示为

M(z)=M(z0) + 0.125(z-z0) -

(3)

式中：z0为海面粗糙度高度；d为蒸发波导高度，当d为0时，表示标准大气的折射率模型.

表面波导是由于陆地干暖气团移动到海面上湿冷气团上空，形成较大的负折射率梯度，从而构成较强陷获作用的表面波导结构，其射率模型可表示为

(4)

式中：M0为海面粗糙度高度处的修正折射率；c1，c2分别为表面波导基础层和逆变层的折射率梯度；h1，h2分别为基础层与逆变层的厚度，当h1为0时，模型表示为不含基础层的表面波导.

2 窄角抛物方程的导出

在折射指数为n的各向同性介质中，场量ψ满足Helmholtz方程[5]

(5)

式中：k为波数;n为介质的折射指数;对水平方向的电波传播而言，x表示水平距离，z表示垂直方向高度.该波动方程有以下形式的解

ψ(x,z)=u(x,z)exp(ikx) .

(6)

将式(6)代入方程(5)中，可得

(7)

此处，引入伪微分算子

(8)

(9)

方程(9)有解

(10)

(11)

代入方程(10)中，可以得到标准窄角抛物方程

(12)

这里使用分步傅里叶变换算法求解该抛物方程，其解经过变换可得

u(x+Δx,z)=exp[ik(n2-1)Δx/2]·

F-1{exp(-ip2Δx/2k)F[u(x,z)]} .

(13)

式中：Δx表示x方向上的步进；p=ksinα，表示垂直空间波数；F(*)表示傅里叶正变换；F-1(*)表示傅里叶逆变换；exp(-ip2Δx/2k)表示传播媒质对电波的折射效应，而exp(-ip2Δx/2k)则反映了电波对障碍物的绕射效应[8].抛物方程算法正是基于式(13)逐步计算空间中各点的电波传播损耗值.

3 误差分析

窄角抛物方程是由波动方程逐步近似演变而来，其推导过程中，存在近似，所以不可避免地产生误差.分析误差产生机理，并且明确因子引起误差的大小，有助于提高计算结果的可靠性.

笔者具体对微分算子Q的近似所产生误差进行分析，由(8)，(11)式中，Q、Q1的表达式，可得两者的平方差表达式

Eerror=Q12-Q2=

(14)

近似过程产生的误差并不是恒定的，而是随着参数的大小变化而变.通过变换式(14)，建立误差Eerror与折射指数变化Δn、传播仰角α两因子之间的关系.在电磁波传播仰角较小的情况下，|μ(u)| ≈ sin2α[9]，大气折射指数接近于1，其变化量为Δn，则n=1+Δn，将以上条件与ε表达式代入到误差表达式中可得

(15)

其相对误差为

(16)

式中：α为电磁波传播仰角.

假设Δn分别为0.01,0.05,0.1,0.2，可得绝对误差、相对误差与传播仰角之间的关系图如图1所示.

由图1中可以得出，传播仰角控制在15°以内时，大气折射指数变化小于0.1情况下，绝对误差比较小，在0.02以内，相对误差也控制在1%以内，而Δn为到0.2时，绝对误差增大到0.05左右，相对误差为4%左右.

图中曲线趋势表明，传播仰角逐步增大，误差与相对误差都相应增大，从而对计算结果产生较大影响，尤其在传播仰角大于20°以后，误差增大更为显著.因此窄角抛物方程不适用于求解传播仰角较大的电波传播过程.一般认为，传播仰角在10°以内，使用窄角抛物方程法计算电波传播损耗能达到足够精度.

下文讨论误差与折射指数变化关系，若传播仰角为5°， 10°， 15°，则误差与折射指数变化之间的关系图为图2所示.

对流层大气当折射指数变化在1.000 25～1.000 4之间，变化量较小.由图2可知，在3种不同天线发射仰角情况下，由折射指数变化Δn引起的绝对误差都在0.001左右，其相对误差也控制在0.1%以内.以上表明折射指数变化引起的误差对计算结果影响较小.

在窄角抛物方程算法计算步长内(一般为100 m～1 000 m之间)，折射指数变化更为细小，可认为恒定不变.所以在窄角抛物方程推导过程中，式(7)假定折射指数不随x变化而变，对窄角抛物方程精度的影响可以忽略.

图1 误差与传播仰角关系Fig.1 Error and elevation angle relationship

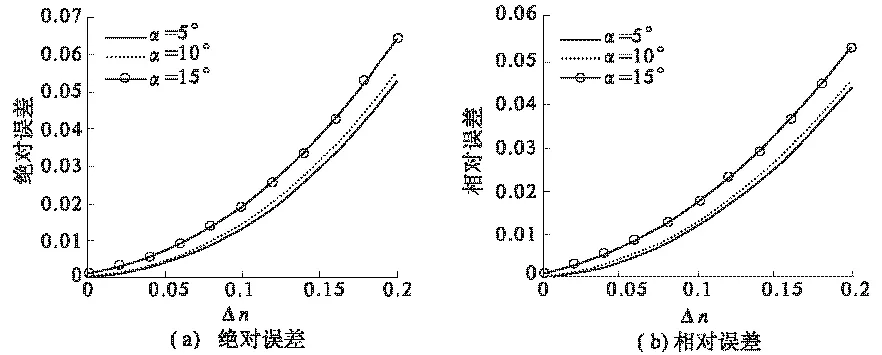
图2 误差与折射指数关系Fig.2 Relative error and refractive index relationship

4 数值算例

使用C语言编程，分别计算了标准大气，蒸发波导，含基础层表面波导3种大气结构的电磁波传播损耗分布；其中，天线发射高度在标准大气与蒸发波导中为10 m，表面波导和含基础层表面波导中为15 m，传播仰角为0°；蒸发波导高度为20 m；含基础层表面波导，基础层高30 m，逆变层高度50 m；电磁波频率为6 GHz；极化方式为水平极化；波束宽度为0.7；海面相对介电常数为70；电导率为5 s/m；垂直步长为0.2 m，水平步长为100 m.

图3～5分别为标准大气及2种波导类型下，电磁波传播损耗分布伪色彩图.

由图3可知，标准大气中，电磁波是偏离水平面传播的，传输距离有限，在距离发射源40～60 km处，传播损耗值就达到了160 dB以上，通信及雷达系统已经不能正常使用；图4显示蒸发波导对电磁波出现陷获作用，计算条件下，波导内传播衰减在100～130 dB之间，衰减值比标准大气要小.由图5可知，含基础层表面波导对电磁波的陷获作用明显大于蒸发波导，同等距离波导内传播衰减也较蒸发波导小并且出现波动情况.少量电磁波在传输过程中，向上传播角度大于波导最大陷获角度，所以表面波导上方出现电波透射出波导情况.

图3 标准大气Fig.3 Standard atmosphere

图4 蒸发波导Fig.4 Evaporation duct

图5 含基础层表面波导Fig.5 Including base layer surface duct

2种波导类型均出现波导传播现象，实际情况中，就有可能实现超视距传播，将大大利于雷达探测等应用.然而，波导上方的区域电磁波传播衰减明显大于波导内区域，该区域可能成为作业雷达的探测盲区.

5 结论

为了求解海平面上空电磁波传播损耗情况，将波动方程经过近似，演变成窄角抛物方程；笔者分析了窄角抛物方程推导过程中Q算子引入的误差，并建立了误差与传播仰角、大气折射指数变化的关系式.结果表明，算子Q通过泰勒近似所推出的窄角抛物方程只适用于传播仰角在10°以内的情况，而求解过程中，水平方向折射指数的变化引起的误差可以忽略，即可近似认为x方向上，折射指数为恒定值.

抛物方程算法是目前求解对流层波导中电磁波传播问题的最主要工具，如何更为准确地求解出电磁波传播衰减值一直是研究人员所探索的问题，此过程中除了建立准确的对流层波导传输模型外，减小抛物方程求解过程中可控输入因子引入的误差，以提高解的准确性也是必不可少的.

[1] 李宏强．电磁波在大气波导环境中的传播特性及基于遗传算法的反演研究[D]．西安：西安电子科技大学理学院，2009．

[2] 周晓平，吴德佩，柳朝阳，等. 电波传播混合路径循迹的算法研究[J]. 郑州大学学报：工学版，2014,35(3)：65-68.

[3] 王红光，张蕊,康士峰，等．大气波导传播的抛物方程模型研究综述[J]．装备环境工程，2008，5(1)：11-15．

[4] 姚展予，赵柏林，李万彪，等．大气波导特征分析及其对电磁波传播的影响[J]. 气象学报，2000，5(5)：606-616.

[5] LEVY M F.Parabolic equation methods for electromagnetic wave propagation[M]. London: The Institution of Electrical Engineers, 2000:15-20.

[6] KUTTLER R, DOCKEY G. Theoretical description of parabolic approximation/ Fourier splitstep method of representing electromagnetic propagation in the troposphere [J] .Radio Science,1991,26 (2)：381-393.

[7] BENHMAMMOUCH O，CAOUREN N，KHENCHAF A. Influence of sea surface roughness on electromagnetic waves propagation in presence of evaporation duct[C]//Radar Conference-Surveillance for a Safer World. U.S.A: Piscataway, 2009：1-6.

[8] OZGUN O. Recursive two-way parabolic equation approach for modelling terrain effects in tropospheric propagation[J]. IEEE Transactions on Antennas and Propagation, 2009, 57(9): 2706-2714.

[9] 姚景顺，杨世兴. 抛物方程模型在海上电波传播中的应用[J]. 电波科学学报，2009, 24(3)： 494-497.

Troposphere Radio Waves Propagation in Duct of Parabolic Equation Method and Error Analysis

YANG Ming-shan1， QIU Zhi-yong1， DU Xiao-Yan2

(1.School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China; 2.Information Engineering University, Zhengzhou 450002, China)

The main error which is introduced in the process of the Narrow-angle parabolic equation derivation is analyzed. Then,the relationship between the approximation error and propagation elevation and atmospheric refraction index changes is established. The established expression ascertains the value of the error brought by the two operators and verifies the reliability of the derivation of narrow-angle parabolic equation in the condition of small changes of propagation elevation and atmospheric refraction index. Finally, the loss values of electromagnetic wave propagation in standard atmosphere, evaporation duct and surface duct are calculated.

troposphere duct；parabolic equation；propagation loss；error

2014-09-22；

2014-11-19

河南省科技厅资助项目(112300410055)

杨明珊(1968-)，女，江西南昌人，郑州大学教授，博士，主要从事电磁波传播，材料的电磁性能方面研究,E-mail:qiuzhi158371@163.com.

1671-6833(2015)01-0101-05

TN011

A

10.3969/j.issn.1671-6833.2015.01.024