基于音乐中的自相似性原则

肖武雄

摘要：该文从音律学切入，精确到四十八平均律中去探究音乐结构的自相似性问题，推导建立自相似性音乐分析的参数设定，并以作曲家陈晓勇钢琴小品《日记I》为例进行求证。

关键词：自相似；维度；分数维；域；陈晓勇

中图分类号：J614.5文献标识码：ADOI：10.3969/j.issn1003-7721.2014.03.004

自相似性是混沌学最主要的理论成果之一。意思是：宇宙中的万事万物，其内部（部分）与整体之间从不同的空间尺度或时间尺度来看都存在相似性。比如自然界中的油漆、泥裂、云、鸡冠花、花椰菜、树叶，医学界的无性繁殖、基因克隆……。同样，音乐艺术领域中自相似性早已存在，主要通过作品的组织结构及音响再现表现出来。如贝多芬的“动机分裂”，勋伯格的“主题一致性”，基本乐理中的音程特征，传统和声学中的三和弦、七和弦无不是自相似性的表现。从音乐分析的角度出发，自相似性应该解构到构成作品的最小单位，类似于电子图形学中的“取样精度”。随着历史的进程，这种取样精度同样在音乐作品中有相应的表现。比如：汉族五声性调式的自相似性，从音程角度看是通过大二、小三、大三、纯四度及它们的转位音程表现的；七声性调式音级是以小二、大二、小三、大三、纯四、增四度及它们的转位音程表现的；十二平均律的自相似音程本质上也是这六个；二十四律的本质音程是在六个特征音基础上再增加六个微分音共十二个音组成。即：

此处的“音素”是以传统乐理计算，即：1/4表示四分之一音，1/2表示二分之一音，1为全音。 来表现。

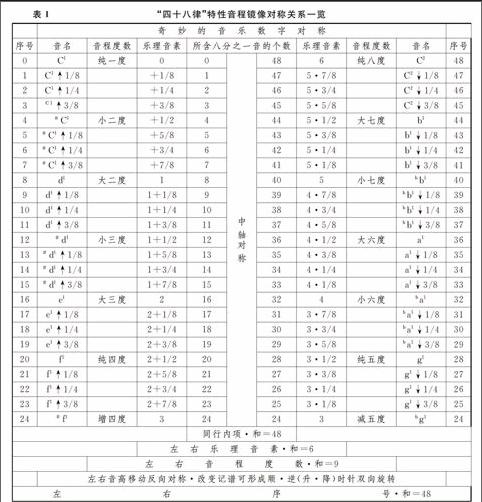
同理，四十八律就有二十四个特征音程构成本质因素。（见表1）

表1把C1至C2一个八度音域空间均分为四十八份，每一个最小单位为八分之一音。传统乐理记为1/8，即C1至C2共48个1/8。以中轴为准，左右两侧严格镜像对称，逆时针旋转音程逐渐增加一个单位（1/8），顺时针旋转音程逐渐减少一个单位（1/8）。#f与bg为等音，音程含量与序号都完全一样。

以上计算了一个八度（六个全音）按照十二、二十四、四十八平均律划分的情况，

即：6×1=6（一个八度有六个全音）

12×1/2=6（一个八度有十二个半音）

24×1/4=6（一个八度有二十四个四分之一音）

48×1/8=6（一个八度有四十八个八分之一音）

表1“四十八律”特性音程镜像对称关系一览

奇妙的音乐数字对称

序号音名音程度数乐理音素所含八分之一音的个数乐理音素音程度数音名序号

神奇的6！无论怎么划分（按偶数、奇数、质数做均分）都能得到中轴对称的音列。而且，永远能分割下去——日取其半，万世不竭。

即：一个八度包含6n 个 1/n ， [ n ∈ ∞ ]

数学表达为：6n × 1/n = 6

由此可见：音乐的自相似性是由“数”这里的“数”针对不同的对象有不同的表现，从音程而言表现为整数、分数；从声音频率、振幅而言表现为整数、小数；从三者的关系而言表现为对数、函数；从空间及声音相位而言表现为度数、正数、负数…… 来表现的，“数”是音乐的根本。如毕达哥拉斯所言：“音乐的美与和谐只能到‘数的关系去寻找”罗塞夫：《古代音乐美学》，莫斯科国家音乐出版社，1960年第1版 ，第16页。 。那么，音乐与数还有什么关系呢？音乐作品中的自相似性如何表达？何为它的最小单位？最小单位如何包含预示整体的属性？要解释这些问题必须先搞清楚两个概念。

1.维度（ dimension ）

维度就是我们分析的目标对象所采用的分析角度，又称维数，是数学中独立参数的数目。在物理学和哲学的领域内，指独立的时空坐标的数目 。

点：是0维，没有长度。表明音乐中绝对的“点”（静止的单音）所谓绝对的“点”结构，只起静止的谱面意义，一旦它触发振动就会有从生到死（发音到消失）的全过程，这一过程中存在许多谐波泛音，所以乐音中的“绝对单音”是不存在的。 是不存在的。

线：是1维，只有长度。表示音乐中的音程距离，如微分音，自然音程等等。

面：是2维，由长宽的两条直线（或曲线）构成的面积。表明任意音向空间两个方向发展都会出现的相应面积。

体：是3维，由长宽高三条相交的直线（或曲线）构成。表明任意音向空间三个方向发展都会出现的相应体积。

场：是4维，三维的世界是静止的，当三维世界以时间为基准发生变化时，四维空间就产生了，如果把时间看作一根轴线，则这个轴线上的任意一个点，都是一个三维空间，也就是说无数个三维空间依据时间轴线集合，构成了四维空间。

传统乐理把自然音程限定在十四种之内，即：“一四五八无大小，二三六七没有纯，外加增四减五”晏成佺、童忠良：《基本乐理教程》，北京：人民音乐出版社2006年版。 。同样，把音乐演奏的时间最低细化到“秒”。这些单位对于极限认识的分形理论而言太过“粗糙”，不准确。当代科技的测试手段，要求各参数精密计算，更加细化，从而找到“最小的自相似性”。认识从极限更接近事物的本源。

2.分数维（fractal dimension ）

19世纪，数学家们发现了分形，由此创立了一种新的维度——“分数维”，人们由此意识到，维度不只是整数，还有可能是分数，甚至可能是无理数！英国著名物理学家史蒂芬·霍金教授有这样的解释：这就像一根头发，远看是一维的线，在放大镜下，它确实是三维的；如果面对时空，如果有足够高倍的放大镜的话，也应该能揭示出其它可能存在的4维、5维空间，直至11维空间。相对于音乐而言微分音就是分数维，理论上可以细分到无穷，即：1/∞。但是，从人们可以感觉和演奏的角度出发，微分音到1/8精度，从创作和演奏上说就已经够用了。从律学角度上说却还需要精细到1/200精度，这正好是一个音分的单位，也是全世界律学通行的精度单位。尽管微分音还可以细分下去，那也是运用于军事科学领域，于音乐作品而言反倒成为了累赘，故而，基本不用。

时间维度，同样可以精细到微妙、纳秒……，但针对音乐组织的频谱分析软件使用的最小单位是毫秒。它们的关系如下：

1s（秒）=103ms（毫秒）=106μs（微秒）=109ns（纳秒）

3.域（domain）

域本身也是一种维度，指客观事物存在的空间范围（静态和动态两种范围）。一切声源都在震动，所以，构成音乐作品的任意一个组织参数都是运动的。音乐艺术领域涉及的域及维度都是具有生命的，具有自身的起始过程，其过程之中反映出的相对稳定属性更值得我们重视。总谱记录的只是谱面静态的域，需要在二度创作变成音响时，才能实现动态而富有生命的域。

点：就是“无”，没有运动，没有生命，也没有域。即：零时空。

线：对应“线域”，在一维条件下，大无终，小也无终（极限接近零）。

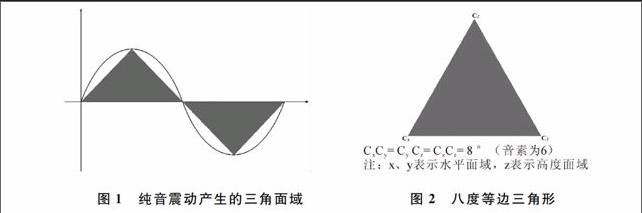
面：对应“面域”，只要琴弦震动，无论琴弦多长，哪怕它短到极限，它也有波峰、波谷及平衡中点，倘若把三者连接起来得到的就是二维面域。（见图1）

图1纯音震动产生的三角面域图2八度等边三角形

我们已知乐音中包含N个纯音，即：琴弦全长震动时，弦上的“N段点”都能产生自己的谐波泛音，所有各段的震动都能构成属于自己的“三角面域”，微分音构成微分三角形，全音程构成全音三角形……下面取一个等边三角形来进一步研究。假设边长等于一个八度。（见图2）

下面取各边长的中点，即：增四（减五）的三全音点（音素为3）把它们构成的三角形挖空。（见图3）

图3八度等边三角形·边长分为二份·图4八度等边三角形·边长分为四份·

三全音量化面域小三度量化面域

同理，再继续剩余三角形边长的一半，量化精度到增二（小三）度（音素为112）。（见图4）

再取所得三角形边长的一半，量化精度到四分之三音（音素为3/4）。（见图5、6）

图5八度等边三角形·边长分为八份·图6八度等边三角形·边长分为十六份·四分之三度量化面域八分之三度量化面域

继续取更小的量化单位十六分之三，边长分为三十二份·还可以得到下列三角形（见图7）：

图7图8八度等边三角形·边长均分五份·

一又五分之一音素量化面域

这样的极限划分可以永远进行下去，从音乐实际演奏的角度到这一步就够用了。这一图形原理运用了谢尔宾斯基“垫片”理论波兰数学家谢尔宾斯基（W.Sierpinski1882—1969 ）以对集合论、数论和拓扑学的出色贡献而闻名，他在1915年提出了垫片理论，是自相似集的一种 。 。上述三角形都是按照“找中点二分法”（类似传统乐理音值组合的基本划分）不断地向下进行。倘若是把边长按照奇数划分，如分为：三、五、七、九、十一………………得到的三角形还会是等边三角形吗？（见图8）

均分三、七、九、十一…结论一样，推理略。

可见：得到的仍然是等边三角形，它就相当于基本乐理中音值组合法的特殊划分。

在此，不禁要问，有无不等边三角形，倘若只有一个边长做任意数目的均分，从该边长外的第三维点（原三角形的高点）向各分段点连线，得到的三角形就是不等边三角形。（见图9）

图9八度等边三角形·边长奇数图10四面体三角形谢尔

划分得到不等边三角形量化面域宾斯基 “垫片”量化体域

从图9各维出发得到的都是三角形，即便由维线相交得到的梯形及更加复杂的多边形，也可以继续划分都能找到更小单位的三角形组织。

从上述推理可以得到下列结论：

1.音乐作品的自相似性在面域上音乐作品的自相似性在线域上是以音程度数（音素）表示的，通常以作品中的最小音程数为单位。 是通过三角形表现（即使在任意小的比例尺度内也包含整体）。

2.任意三角形的三个顶点构成一个三和弦，四边形（梯形）可分为两个三角形。即：传统七和弦可以拆分为两个三和弦。

3.N面体最少包括N个三和弦，极限划分存在无穷个三和弦。

4.音响的存现形式是立体的，具有时空属性。上述所有三角形的划分都是在“静态场景”（谱面意义）中的分形压缩。实际运用还需要考虑音响的多维属性。

5.音乐就是三角形（三和弦）的集合可能有人会反问，如单一声部独奏，三角形在哪里？传统谱面记录的单旋律表面看是一维曲线，实际上是立体四维时空呈述，用频谱仪可以把每一个阶段参数记录下来。通俗地说就是：音响是以声场的传输转移来实现的，谱面旋律的任何一个单音都构成以它为基音的谐波系列（声场），旋律音响是声场的有序集合。 。

6.阴阳、生死、分合、虚实体现分形构成的空间秩序和永恒法则。（见图10）

由此，可见音乐音响分析的难度。

因为自相似性在任何时期、任何流派、任何作曲家的作品中都大量存在，仅仅是名词使用不同而已，无需赘述。下面仅以陈晓勇钢琴小品《日记I》第一首《上发条的小鸡》（Clockwork Chicken）为例，从线域、面域、体域角度寻找作品的自相似性。

作品的核心材料来源于三个音，整个作品是由“g-ba-a-bb”四个音构成的四面立体时空体域构成，四面分别是：bb-a-g、bb-g-ba、b-a-ba、ba-a-g，再由它们闭合成一个四面体。见下图：

线域特征面域特征体域特征

图11陈晓勇《上发条的小鸡》线域一、面域一、体域将位示意

通过乐谱可见，作品可以分为三个段落。

A.呈示段

1.面域呈示：由“g-bb-a”三角形构成，演奏音色使用两种方式： ①抑制音（dampened）奏法用左手摁住琴弦，抑制弦振动，尽量发出只有音头的干音。 ，乐谱记为实音黑符头②余音（正常完全振动ordinary）奏法琴键触弦瞬间，左手立刻离开琴弦，让琴弦充分振动，发出所有谐波泛音。 ，乐谱记为方块符头。原型呈示以后，紧接着逆行呈示。

谱例1陈晓勇《Clockwork Chicken》呈示段核心材料面域呈述

2.体域呈示：由“g-bb-ba-a”四面体构成。体域呈示以后又回“g-bb-a”三角形构成的面域呈示。可见，呈示段本身具有“再现性”。

B.派生中段

如果说呈示段是演奏法的一维线性呈述，那么派生中段就是演奏法的二维对位，即把呈示段的两种演奏法“化横为纵”形成“虚实相映”的对比复调二维呈述。

谱例2陈晓勇《Clockwork Chicken》派生中段演奏法二维对比

谱例2中上方声部持续的a音是一道看不见的风景，下方的“bb-g”形成的循环断奏由于抑制了琴弦振动，只发出基频音高，而几乎没有泛音。相反由于a键琴弦共振而产生一系列谐波泛音，也就是说a弦成为了bb-g的共鸣箱，而bb-g两弦是发生器。

可见，谱面的风景是“实比虚好看”，实际音响画面却是“虚比实精彩”，这从又一个侧面证明了作曲家喜欢的隐性原则。中段不停地用“a-ba”两音来做虚轴共鸣，实音抑制演奏保持呈示段特点，在另外两个（或三个）音点上轮回，整体始终保持面域（或体域）特征。

C.总结性综合变化再现

再现对映呈示也具有三部性原理。

1.面域再现：由“g-bb-a”三角形构成，先回到演奏法（抑制音与余音），一线呈述方式。

2.体域再现：演奏法虚实二维对位，虚用加法，增加为四个音。实用减法，先用“bb-a”两音，再逐渐拉长稀释停到bb音上，收拢全曲。

上述分析可见：三角形自相似性分析能够帮助我们从立体时空角度去把握作品的组织结构，把谱面静态场景的音高变成多维时空，立体地呈现出来。从而让我们发现许多传统分析无法触及的领域。

值得注意的是：自相似性分析所提炼的参数单位要相对统一。比如上述各例是从音高角度分析，还可以从音色、力度、时值、相位、密度……各参数分析。倘若混合参数，分析将更加繁杂。

自相似作为对称性的一种，是科学地或者哲学地把握世界的一种范式、工具。它打破了整体与部分之间的隔膜，找到了部分过渡到整体的媒介和桥梁——整体与部分之间的相似。是古代哲学思想在近代自然科学中的重现：

一性圆通一切性，一法遍含一切法。一月普现一切月，一切水月一月摄。

——玄觉《永嘉证道歌》玄觉：《永嘉玄觉禅师证道歌讲析》，成都：四川巴蜀书社2006年版。

这种在一刻钟把握永恒，“一沙见世界，一花窥天堂”的自相似性是艺术作品自我组织的根本原则。同时，我们也要清醒地认识到分形理论不是万能的，它只是一种方法或规则。在事物整体之中还存在着惊异的混沌。

（责任编辑：张璟）