表面阻抗法测量水声材料声反射系数误差分析

时胜国，王超，胡博

(1.哈尔滨工程大学水声技术重点实验室，黑龙江哈尔滨150001;2.哈尔滨工程大学水声工程学院，黑龙江哈尔滨150001)

声学材料声反射系数是表征其声学性能的重要参数，主要测量方法有阻抗管法、混响室法和自由场法等。阻抗管法［1-3］测量频率范围有限且仅能测量小样品法向声反射系数，无法真实反映实际应用中大样材料的声学特性;混响室法［4］仅能测量无规入射吸声系数且稳定性欠佳。上述方法已得到了广泛应用且有相应的测量标准。自由场法可以完成大样品测量，能够更加真实地反映材料在实际应用中的声学特性。自由场方法会受到材料边缘衍射效应的影响。为了规避边缘衍射效应，人们提出了各种改进测量方法，如宽带脉冲叠加法［5-6］、指向性声源测试法［7］等。近年来，随着矢量传感器及其信号处理技术的发展，矢量传感器已经应用于空气声学测量［8-10］领域。它可以同步、共点地测得声场某点声压和质点振速信息，经过简单计算可得到材料表面声阻抗率，进而计算得到材料声反射系数。与传统双声压传声器法［11-13］相比，矢量传感器余弦接收指向性可以有效规避材料边缘衍射效应，提高声反射系数测量精度。

单矢量传感器表面阻抗法的测量精度主要取决于测量原理、发射声源和测量系统等参数。文献［9-10］主要讨论了声源到样本的距离、矢量传感器到样本距离和样本尺寸大小等参数对测量结果的影响，但并未对表面阻抗法的测量误差来源和测量不确定度进行理论分析。本文系统地分析了基于单矢量传感器表面阻抗法的测量误差来源和影响大小，主要从边缘衍射效应和测量系统参数误差两方面进行理论分析，为实际工程应用提供指导性意见。

1 表面阻抗法测量理论分析

1.1 表面阻抗法测量原理

图1中S为一点声源，h为声源到材料表面距离，r1为声源到矢量传感器距离，r2为虚源到矢量传感器距离，d为矢量传感器到材料表面距离，θ为声波入射角。

图1 表面阻抗法测量模型示意图Fig.1 Schematic diagram of the surface impedance method

直达波声压与法向质点振速为

式中:k为波数，ρ0为介质密度，c为介质声速，p0为声源辐射声压幅值。材料声压反射系数为R，则反射波声压与法向质点振速为

则材料表面声阻抗率为

材料声压反射系数为

若kr1≫1，则式(6)化简为平面波表达式:

1.2 衍射效应计算模型

图2中S为声源，R为水听器，A、B、C、D为矩形待测材料四边中点，n为法向量，声波以角度θ入射，材料四边长均为L，声源、水听器到材料距离分别为h和d，θr1、θr2、θr3、θr4为四边衍射角，θs1、θs2、θs3、θs4为入射声波与材料表面夹角，β1、β2、β3、β4分别为入射波与材料边缘夹角，Ped1、Ped2、Ped3和Ped4分别为四边衍射波，A、B和Rs1、Rs2、Rs3、Rs4分别为接收点和声源到材料四边距离，球面波入射时边缘衍射系数公式［14］为

式中:矩形板取n=2，Ru、Rd分别为样本两侧复反射系数，k为波数，F(*)为修正形式的菲涅尔积分，参数Δ1、Δ2、Δ3和Δ4为

总衍射声压为

图2 边缘衍射模型示意图Fig.2 Schematic diagram of the diffraction effect

1.3 测量不确定度分析

设间接测量量Y的估计值y由n个直接测量量x1，x2，…，xn的函数计算求得，即:

则测量结果y的合成标准不确定度为［15］

式中:∂f/∂xi为灵敏系数，ρij为任意2个不确定度的相关系数。单矢量传感器表面阻抗法测量材料反射系数依赖于直接测量量H、d、θ和间接测量量阻抗率Zm的测量。Zm的测量相对合成不确定度为

式中:u(p)/p与u(v)/v分别为声压和质点振速的相对不确定度，由矢量传感器的性能决定。测量系统的测量不确定度及自由度为

式中:u(*)为各个测量量的标准不确定度，vi为各标准不确定度分量ui的自由度。

取H、d和 θ的不度定度为 u(H)=0.3δH，u(d)=0.3δd和u(θ)=0.3δθ。设测量仪器分辨力为δH=0.01 m，δd=0.001 m，δθ=1°，当信号频率和声波入射角度分别为2 kHz和θ=30°时，uRc随声波入射角度和频率变化规律如图3所示。

图3 测量不确定度Fig.3 Uncertainty of the measurement

由图3可知合成标准不确定度随声波入射角度变大而变大，随频率升高而减小。所以在低频、大角度入射情况下应严格控制测量系统参数布放精度，减小测量系统参数误差对测量结果的影响。

2 表面阻抗法测量误差分析

本节仿真中，若无特殊说明，测量样本均为铝板，板厚0.006 m，几何尺寸1 m×1 m，矢量传感器到材料表面距离d=0.05 m，声源到样本距离H=5 m，信号频率为500～10 kHz，频率间隔为1/3倍频程。

2.1 测量原理的误差分析

仿真条件1:信噪比SNR=60 dB，声波入射角θ=30°，声源到样本距离分别为H=2 m和H= 5 m，计算复反射系数模值随频率变化情况。

图4给出了2个计算模型的计算结果，可见球面波计算模型精度高;平面波计算模型在低频段误差较大，但声源越远误差越小。本文仿真均采用球面波测量模型。

图4 不同模型测量结果Fig.4 Measurement result of different models

2.2 材料边缘衍射效应的影响分析

仿真条件2:采用双声压水听器法和单矢量传感器表面阻抗法测量，声波入射角θ分别为0°、30°、60°。

图5 测量结果对比图Fig.5 Contrast of the measurement results

图5给出了单矢量传感器表面阻抗法和双声压水听器法的测量结果。可见边缘衍射效应对2kHz以下频段影响较大，误差随声波入射角度变大而变大，测量有效频率下限随声波入射角度变大而升高;单矢量传感器表面阻抗法性能优于双声压水听器法，小角度入射情况下测量更准确。为了抑制边缘衍射，也可将矢量传感器偏心放置，破坏样本各边衍射波的干涉，减小边缘衍射影响。矢量传感器偏离样本中心5 cm布放，测量绝对误差如图6所示。

由图6可知矢量传感器偏心放置后最大误差约为0.06，而同心放置测量结果最大误差约为0.12。相较而言，除个别频点外，偏心放置测量误差较小。

边缘衍射效应也可以通过增大样本尺寸得到抑制。分析频率为500 Hz，样本边长L=2m。测量误差随声波入射角度变化如图7所示。

图6 绝对误差随频率变化曲线Fig.6 Absolute error versus frequency curve

图7 绝对误差随角度变化曲线Fig.7 Absolute error versus angle curve

由图7可见增大样本尺寸可以抑制衍射效应，测量绝对误差随入射角度变大而变大。

综上仿真结果表明:矢量传感器对抑制边缘衍射效应起到了一定作用;测量时矢量传感器应偏心放置或选取较大尺寸样本。

2.3 测量系统误差分析

2.3.1 发射信号信噪比影响分析

仿真条件3:信噪比 SNR分别为－10、10和30 dB，声波入射角θ为0°。

由图8可见当信噪比为－10 dB时测量结果符合理论变化趋势，当信噪比达到10 dB时误差可忽略。

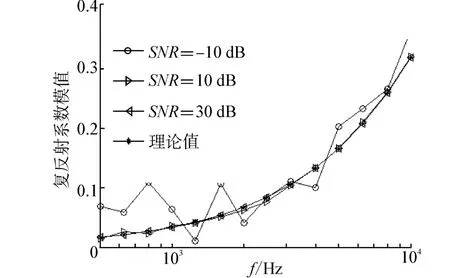
图8 不同信噪比测量结果Fig.8 Measurement result in different SNR conditions

2.3.2 矢量传感器各通道声压灵敏度误差及相位一致性影响分析

矢量传感器对表面阻抗法影响主要有声压、质点振速通道间相位一致性影响和灵敏度误差影响。

仿真条件4:信噪比SNR=60 dB，声波入射角度为0°，讨论矢量传感器声压、质点振速通道间相位差△Φpu分别为2°、3°、4°和5°时测量结果。

由图9可见矢量传感器声压、质点振速通道间相位一致性对测量结果影响较大。测量频率小于6.3 kHz计算结果误差较大;测量对矢量传感器相位一致性敏感。图中Φ为复反射系数R的相位。

图9 相位一致性影响Fig.9 The effect of the phase consistency

仿真条件5:信噪比SNR=60 dB，声波0°入射，矢量传感器声压与质点振速通道灵敏度误差△Mp与△Mu分别为1、2和3 dB时测量结果。如图10所示。

由图10可见矢量传感器各通道声压灵敏度误差对测量结果影响较大;当声压通道或质点振速通道声压灵敏度存在2 dB误差时模值测量失效;相位测量对矢量传感器灵敏度误差敏感，灵敏度存在1 dB误差时测量失效。

图10 测量结果对比图Fig.10 Contrast of the measurement results

测量时应首先对矢量传感器进行灵敏度校准。灵敏度校准采用比较法校准。另外，应对测得的阻抗进行修正，声源为点源时可得矢量传感器处波阻抗Z0，实际测得的波阻抗为Zm，则修正因子为

2.3.3 测量系统布放误差影响分析

仿真条件6:矢量传感器到样本距离d分别为0.05、0.1、0.15和0.2 m，信噪比SNR=60 dB，H布放存在1%误差。以声波0°入射和500 Hz时测量为例。

图11给出了H布放不准确引起的相对误差变化规律，可见在法向入射时最大相对误差约为2.7%，在500 Hz时测量最大相对误差约为5.2%。复反射系数测量在低频、大角度入射时易受其影响，此时应控制声源布放精度减少测量误差。

图11 相位一致性影响Fig.11 The effect of the phase consistency

仿真条件7:信噪比SNR=60 dB，声源到样本距离H=2、3、4和5 m，d布放存在10%误差。

由图12可见声源距离越远误差越小;声波法向入射时，模值测量最大相对误差小于1.5%;频率为500 Hz时，入射角度大于40°测量相对误差变大。复反射系数相位测量误差随频率、入射角度变大而升高，且对矢量传感器布放的误差较为敏感。

仿真条件8:信噪比SNR=60 dB，若样本在旋转时存在0.2°角度误差，测量误差如图13所示。

由图13可见，模值测量相对误差不超过0.4%，相位测量相对误差不超过0.2%，可见表面阻抗法对θ不准确不敏感。

图12 d布放引起的相对误差Fig.12 The relative error caused by d

图13 θ旋转引起的相对误差Fig.13 The relative error caused by pivoting θ

综上仿真结果表明:单矢量传感器表面阻抗法在低频大角度入射时测量精度易受系统参数误差的影响;矢量传感器灵敏度误差和相位一致性对测量结果影响最大，测量时可应用式(15)对阻抗进行修正。另外，在低频、大角度入射时更应尽量控制系统布放准确性以保证测量结果精度。

3 结论

本文系统地分析了单矢量传感器表面阻抗法的误差来源，分析了材料边缘衍射效应对测量结果的影响;同时，分析了测量计算模型精度、测量环境和测量系统参数误差的影响。对比仿真计算结果得到以下结论:

1)球面波计算模型精度较高;平面波计算模型在低频、大角度入射情况下误差较大，测量时声源布放应满足远场条件。

2)矢量传感器对抑制边缘衍射效应起到了一定作用，其测量性能优于双声压水听器法;边缘衍射效应在低频、大角度入射情况下影响较大;另外，为了规避材料边缘衍射效应，矢量传感器布放应适当偏离样本中心位置。

3)单矢量传感器表面阻抗法对测量环境信噪比的要求较低，信噪比在10 dB以上即可得到满意的测量结果;但对矢量传感器相位一致性和灵敏度误差敏感，在实际测量时应利用修正因子CF对测量得到的表面声阻抗率进行修正，再计算材料的声反射系数。

4)总的来说，在低频、大角度入射时表面阻抗法对测量系统H和d参数误差较敏感，对θ参数误差不敏感;测量时声源应尽量远离待测样本，矢量传感器应尽量靠近样本;在低频、大角度入射时更应注意控制系统参数误差，提高测量精度。

［1］庞业珍.基于传递函数的吸声隔声测量方法与应用研究［D］.大连:大连理工大学，2005:17-20.

PANG Yazhen.Methods and applications of sound absorption and insulation measurement based on the transfer functions［D］.Dalian:Dalian University of Technology，2005: 17-20.

［2］罗马奇，李水，易燕，等.水声材料低频声性能行波管测量系统的改进及实验［J］.声学技术，2009，28(4):59-62.

LUO Maqi，LI Shui，YI Yan，et al.Improvement and experiments of traveling wave tube measurement system for lowfrequency properties of underwater acoustic materials［J］.Technical Acoustics，2009，28(4):59-62.

［3］曲波，朱蓓丽.驻波管中隔声量的四传感器测量法［J］.噪声与振动控制，2002(6):44-46.

QU Bo，ZHU Beili.Four-microphone method of sound transmission in the standing wave tube［J］.Noise and Vibration Control，2002(6):44-46.

［4］侯宏，徐士化.近代现场吸声测量技术［J］.声学技术，2007，26(6):1209-1213.

HOU Hong，XU Shihua.A review of modern in-situ sound absorption measurement techniques［J］.Technical Acoustics，2007，26(6):1209-1213.

［5］李水，缪荣兴.水声材料性能的自由场宽带压缩脉冲叠加法测量［J］.声学学报，2000，25(3):248-253.

LI Shui，MIAO Rongxing.Measurements for the properties of underwater acoustic materials by broadband compressed pulse superposition method［J］.Acta Acustica，2000，25 (3):248-253.

［6］李水，罗马奇，易燕，等.水声材料构件声学特性自由场宽带测量装置［J］.声学学报，2011，36(5):534-541.

LI Shui，LUO Maqi，YI Yan，et al.The broadband measurement facility for acoustic characteristics of underwater acoustic materials in free fields［J］.Acta Acustica，2011，36 (5):534-541.

［7］姬培锋，杨军，李晓东.基于指向性声源的吸声系数测量［C］//全国声学学术会议论文集.厦门，中国，2006: 495-496.

JI Peifeng，YANG Jun，LI Xiaodong.Sound-absorption coefficient measurement based on the directional speaker［C］//Symposium of Acoustical Society of China.Xiamen，China，2006:495-496.

［8］LANOYE R，DE BREE H E，LAURIKS W，et al.A practical device to determine the reflection coefficient of acoustic materials in-situ based on a Microflown and microphone sensor［J］.ISMA，2004，1(8):2665-2675.

［9］LANOYE R，VERMEIR G，LAURIKS W，et al.Measuring the free field acoustic impedance and absorption coefficient of sound absorbing materials with a combined particle velocity-pressure sensor［J］.The Journal of the Acoustical Society of America，2006，119(5):2826-2831.

［10］HIROSAWA K，TAKASHIMA K，NAKAGAWA H，et al.Comparison of three measurement techniques for the normal absorption coefficient of sound absorbing materials in the free field［J］.The Journal of the Acoustical Society of A-merica，2009，126(6):3020-3027.

［11］陈克安，曾向阳.双传声器法测量斜入射吸声系数研究［J］应用声学，1999，18(4):28-32.

CHEN Ke'an，ZENG Xiangyang.A study on the measurement of sound absorption coefficient at oblique incidence by the use of two-microphone technique［J］.Applied Acoustic，1999，18(4):28-32.

［12］TAKAHASHI Y，OTSURU T，TOMIKU R.In situ measurements of surface impedance and absorption coefficients of porous materials using two microphones and ambient noise［J］.Applied Acoustics，2005，66(7):845-865.

［13］ALLARD J F，SIEBEN B.Measurements of acoustic impedance in a free field with two microphones and a spectrum analyzer［J］.The Journal of the Acoustical Society of America，1985，77(4):1617-1618.

［14］LIU Yansen，SHENG Meiping，WANG Meiyan，et al.Modeling and calculating on the diffraction acoustic field originated from underwater flat structure with finite impedance surface［J］.Journal of Ship Mechanics，2009，13 (6):1002-1012.

［15］吴石林，张玘.误差分析与数据处理［M］.北京:清华大学出版社，2010:175-193.