高Re数下变截面正八边形结构绕流特性试验研究

姚熊亮，王伟，杨娜娜，郭占一

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

随着世界范围内海军竞争的加剧，发展具有优良隐身性能舰船的目标也走上各国军事舞台。作为舰艇“耳目”的桅杆因处于最高点首当其冲，原有的桁架式桅杆已被目前的具有倾斜侧壁的筒形封闭式桅杆所替代，而综合集成桅杆因良好隐身性展现出巨大的优势［1-3］，所搭载的复合材料天线罩采用薄壁无加强筋式结构针对其外形绕流特性研究，保证结构在极限恶劣海况正常工作。

目前针对结构绕流特性的研究，大多局限于具有圆形或方形截面的柱体结构［4-6］，主要研究方法包括试验研究［4，7］、理论研究［8］和数值模拟［4-7］，其中数值模拟在近些年展现出强大的生命力，逐渐发展出LBM［9－10］、RANS_LES［11］等方法，研究方向从单柱绕流问题扩展到群柱绕流耦合［7，10，12］问题，但关于具有倾斜侧壁柱体绕流研究较少，研究对象分为3种:具有倾斜曲面外形的旋转体结构，如K.Lam和Y.F.Lin［13-14］研究Wavy Cylinder的绕流问题;具有圆形或方形截面的倾斜柱体结构，其中Ali Vakil等［14-15］研究有限长度倾斜圆柱在中等Re数下的升力与阻力系数问题;具有相似截面形状和直壁面的棱柱式结构，如姚熊亮等［16-17］开展试验研究五边形、八边形筒形桅杆的风载特性，清华大学田中伟［8］主要通过理论方法结合 CFD研究 Re数和Strouhal数随多边形边数的变化规律。但此类研究多集中于简单的几何截面，关于多边形变截面的研究相对较少，本文研究对象为雷达天线罩结构，截面形状为正八边形，通过开展风洞试验研究结构的绕流特性，为其结构设计提供相关的载荷设计依据。

1 试验设计

1.1 试验原理

天线罩结构为复合材料制造，考虑到风洞截面尺寸，采取缩比钢质模型开展试验研究结构绕流特性。根据π定理可知，试验流场与真实流场中表征流场参数的压力等可相似转换的前提是流场的相似准数相等，而在试验Re＞106的情况下，结构风载特性主要与流体粘性有关，惯性力效应即Fr数可忽略，因此保证流场的Re数相等即可保证流场的相似性。

1.2 试验模型

试验模型为变截面正八边形结构，满足其纵剖面积小于风洞横截面积10%的要求，为测定结构的风载特性，沿垂向自下至上在8个截面上均匀布置384个测点，如图 1所示。每个测点开设孔径1.5 mm的测压孔，插入直径Φ=1 mm，长度为15 mm的钢管并固定，钢管一端通过塑料软管连接到测压仪，同时打磨模型表面，保证结构表面光滑以减小表面粗糙度对流场的影响，以此测定结构表面的稳态压力，研究各定常系数的分布规律。同时，通过六分量测力天平测定结构在不同Re数时的气动力。

图1 试验模型与测点布置Fig.1 Test model and arrangement of measuring points

1.3 试验方法与工况

为了消除洞壁边界层的影响，设计八边形棱柱基座连接模型和六分量测力天平，且基座与模型之间采用迷宫形式的密闭方式防止串流，以此将结构整体固定在风洞底部旋转平台上。

试验时风洞内部温度为20.35℃，标准气压，将模型的最大截面的内切圆直径作为特征长度，试验Re数范围为2.224 2×106～8.896 9×106。考虑到结构的对称性，设计试验风向角β为0°、12°和22.5°，其中风向角和测点相对中心O的方向角θ定义如图2所示。

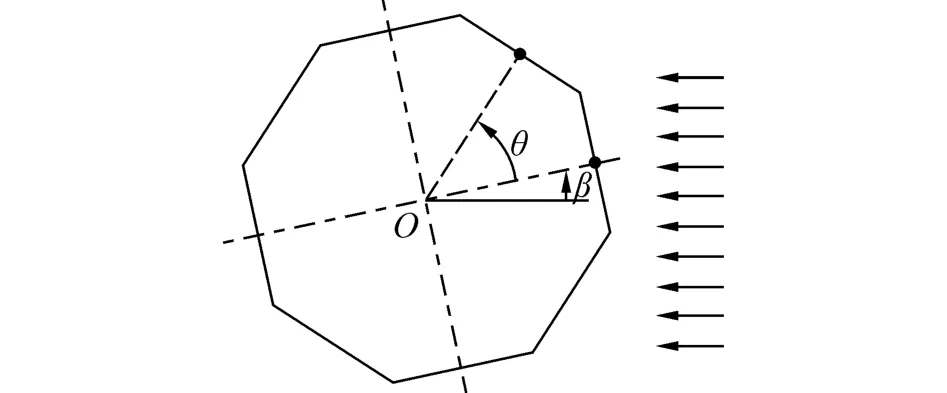
图2 风向角β和测点方向角θ示意图Fig.2 Sketch map of wind direction β and direction angle θ of measuring point

2 试验结果分析与讨论

2.1 平均压力系数CP周向分布规律

在Re=5.1898×106下开展了3个风向角β=0°、β =12°和β=22.5°时各5次重复性试验，保证试验数据的准确性，初步得到结构的周向平均压力系数分布情况，随机选择不同风向角下不同截面的压力分布曲线，如图3所示，可知后2个风向角对应曲线的重复性较好，而β=0°对应的曲线的一致性相对较差，且主要出现在边界层分离区的近后方区域，但影响幅值十分有限，说明测试系统正常、数据可靠。

现以β=0°对应的周向分布曲线为例分析，如图3(a)，平均压力系数在周向上整体呈对称分布，最大平均压力系数CP=1.0出现在迎流面驻点附近，两侧压力略有下降，在θ=22.5°和θ=327.5°附近时第一次出现压力骤降现象，且CP＞0，因折角的存在导致结构迎流面驻点附近由流体动能转化的压能重新转换为动能，并在导致θ=67.5°和θ=292.5°附近持续降低直至极小值CP=－2.5。相比文献［7］边界层分离点CP=－2.3，两者略有不同，同时流体速度达到极大值，进而产生边界层发生分离现象，并附带漩涡脱离，在结构后方区域生成尾涡区，且耗散大量动能，导致结构背流面压力回升，基本稳定在CP=－0.75左右。

2.2 Re数对平均压力系数CP的影响

在2.224 2×106≤Re≤8.896 9×106范围内开展9组不同Re数对应的风洞试验，选取β=0°时截面2对应的周向平均压力系数随Re数的变化曲线，如图4所示。整体上，Re数的影响主要集中在折角位置(方向角θ在22.5°和327.5°附近)和边界层分离区域的后方(方向角θ为67.5°～112.5°和247.5°～292.5°)，为考察Re数对该部分区域CP的影响趋势，选择区域中典型位置测点作为考查对象，同时将迎流面和背流面中点位置测点的Cp变化作为参考，如图4所示。

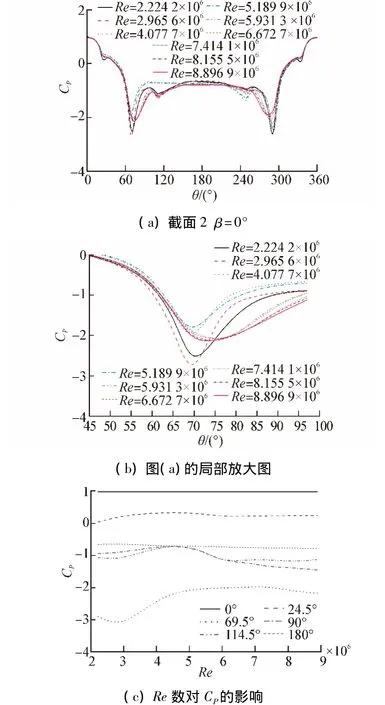
图4 Re数对平均压力系数的影响曲线Fig.4 Influence of Re number on average pressure coefficient

可知方向角θ=0°和θ=180°对应的测点位置的CP基本不随Re数变化，前者维持在CP=1.0，后者维持在CP=－0.75，表明试验Re数均明显大于临界Re数，惯性力起主导作用，趋近于理想流体流动，Re数对结构表面流动稳定区域的影响非常微弱，基本可忽略;相比而言，折角与边界层分离区对试验Re数较为敏感，90°和114.5°对应测点位置的CP呈现出先上升后下降的趋势，但升降幅值较小，最后趋向于常值;而θ=24.5°测点位置的CP变化趋势与前两者相近，且幅值更小并稳定于CP=0.20;受Re数影响最大的是位于θ=69.5°位置测点，即边界层分离点，表现为小幅下降后大幅上升，变动幅值在1.0左右，最后逼近于CP=－2.20，因为高Re数导致边界层转变为湍流边界层，在折角位置发生边界层分离，形成漩涡，并在结构尾部形成尾涡区，导致流体动能耗散，表明流体在该部分区域流动的不稳定性，尤其体现在边界层分离区，进一步表明高Re数对周向Cp的影响不可一概而视。

2.3 风向角β对平均压力系数CP的影响

选取Re=5.189 9×106时截面4的周向平均压力系数作为考察对象，为便于对比不同风向角下相同方向角位置的CP，现对曲线作如下处理:将方向角与风向角之和(θ+β)作为新的方向角θ'，处理后的曲线如图5所示。

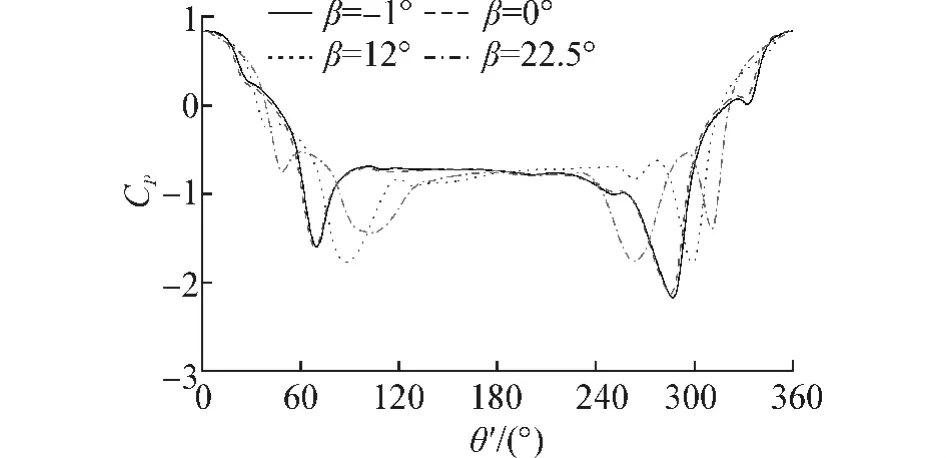
图5 风向角β对平均压力系数CP的影响Fig.5 Influence of wind direction β on average pressure coefficient CP

可知:

1)对沿迎流面法向空气流动速度分量的影响，主要表现在峰值两侧平均压力系数CP的下降速率，即在0°≤θ'≤22.5°范围内，风向角β越大，下降速率越快，但当22.5°≤θ'≤34.5°时现象发生逆转，主要是因为风向角不同导致迎流面与流场方向之间的夹角不同，进而导致绕流流场发生变化，如不同风向角对应的第1次压力骤降方向角θ'不同，β=0°对应θ'=22.5°，而后两者分别对应θ'=34.5°和θ'=45°，且三者对应的压力系数也逐渐降低。

2)对边界层分离点和分离强度的影响，表现为平均压力系数CP极小值及其位置的变化，β=0°和β=22.5°分别在θ'为67.5°和292.5°、θ'为100°和260°出现一对极小值，且呈现出明显的对称性，而β=12°对应的极小值则出现在θ'=90°和θ'=300°附近，主要原因是边界层分离点的移动方向与流场转动方向β的一致，但沿流场方向中心线两侧结构的不对称性以及结构的外形导致边界层分离点的移动相对滞后，因此风向角对边界层分离点强度影响的规律性有待进一步研究，但在本试验中相比其他2个风向角，β=12°对应的分离强度明显较弱。

3)风向角对尾涡区结构表面的压力分布影响较小，CP基本维持在－0.75～－0.80。

2.4 倾角α对平均压力系数CP的影响

任意选取Re=5.189 9×106时2个截面，分析具有相同倾角截面周向压力分布对垂向位置的敏感性，如图6所示，截面2与截面3在不同风向角下的平均压力系数基本重合，因此在倾角相同的情况下可忽略垂向位置因素的影响。

图6 相同倾角截面周向平均压力系数对比Fig.6 Contrast of circumferential CPof sections with equal inclination

因此，选择Re=5.189 9×106工况对应2种风向角β=0°和β=22.5°下具有不同倾角α的结构平面，将相应截面上的边界层分离点(β=0°对应292.5°、β=22.5°对应247.5°)和驻点位置(β=0°对应0°和180°、β=22.5°对应157.5°和337.5°)平均压力系数作为考察对象，如图7所示。考虑到相同倾角下位置对流场的影响甚微，可知:

1)迎流面驻点位置的平均压力系数基本上随倾角的增大而降低，主要原因是倾角直接影响流场沿迎流面的法向速度分量，进而导致迎流面风载降低，与风向角对驻点压力系数的影响基本一致;

2)倾角的改变对背流面驻点位置的风载几乎无影响，基本稳定在－0.75≤CP≤－0.80，主要因为背流面驻点位于边界层分离点后侧，考虑到试验Re数均已超过临界Re数且倾角的改变对流场的影响有限，也进一步表明高Re数时结构迎流面的倾角α的变化对尾涡区流场的影响微弱;

3)边界层分离点后方的平均压力系数受倾角的影响规律相似，呈现出先升高后降低、再缓慢上升的趋势，但β=0°对应的曲线始终在CP=－2.2左右浮动，幅值很小，且两者不同于不同风向角β下驻点位置CP随倾角变化规律的高度一致性，两者表现出0.5～1.0的差距，表明β=0°对应的边界层分离强度高于β=22.5°，与上一节结论相同。

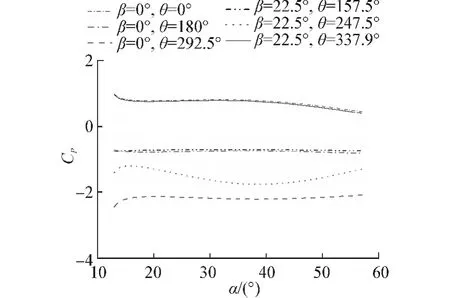
图7 倾角α对平均压力系数的影响Fig.7 Influence of inclination α on average pressure coefficient

2.5 Re数对气动力系数的影响

将试验模型视为一种特殊翼型，根据相关标准确定阻力D逆流场方向为正，升力L指向垂直流场的模型的侧向，而侧力C沿模型轴向指向外侧。测得结构在3个风向角下的阻力系数CD、升力系数CL和升阻比L/D以及侧力系数CC随Re数的变化曲线如图8和图9所示，可知:

1)在3个风向角下阻力系数整体上随Re数的增大而上升，分析原因为高Re数情况下形状阻力为粘性阻力的主要成分，且由2.2节可知试验Re数的升高主要影响边界层分离点近后方区域的压力分布，导致区域内风载升高，进而引起结构整体遭受的阻力系数也小幅升高;

2)Re数的变化对升力系数的影响与风向角的相关性较显著，β=0°下升力系数在CL=0.10水平上作幅值为0.02的波动，β=12°对应的升力系数整体呈现出降低趋势，最大幅值为3.7×10－2，相比之下β=22.5°对应的升力系数趋势相反，从最低0.278上升到最高0.316，升幅达13.7%，主要是考虑到试验Re＞106，湍流尾迹中出现明显的周期性漩涡再现或重组，且模型表面的粗糙度及其外形的非严格对称性都有可能导致升力系数的不稳定;

3)升阻比L/D的变化趋势表现出与升力系数高度的一致性;

4)在3个风向角下侧力系数基本先呈现出不同幅值的下降，随后呈波动性稳定，且与阻力系数和升力系数没有明显的关联性，原因可能是侧力系数主要由结构周向载荷在垂向的分量与上表面风载2部分贡献，虽然周向平均压力系数基本均随Re数收敛，但从阻力系数与升力系数随Re数的变化可得出边界层分离点附近分离强度和影响范围的差别同样造成整体结构载荷变化的结论，且结构截面突变位置的影响也可能对局部压力的分布产生影响，并且推断上表面风载随Re数呈一定的变化规律，因此认为是2种载荷的所占比例的变化影响侧力系数的变化规律。

2.6 Re数对气动力矩系数的影响

同气动力的定义类似，根据机翼的航行状态将力矩分为滚转力矩、俯仰力矩和偏航力矩。为考察不同风向角下Re数对滚转力矩系数Cl、俯仰力矩系数Cm和偏航力矩系数Cn的影响，绘制曲线如图10所示。

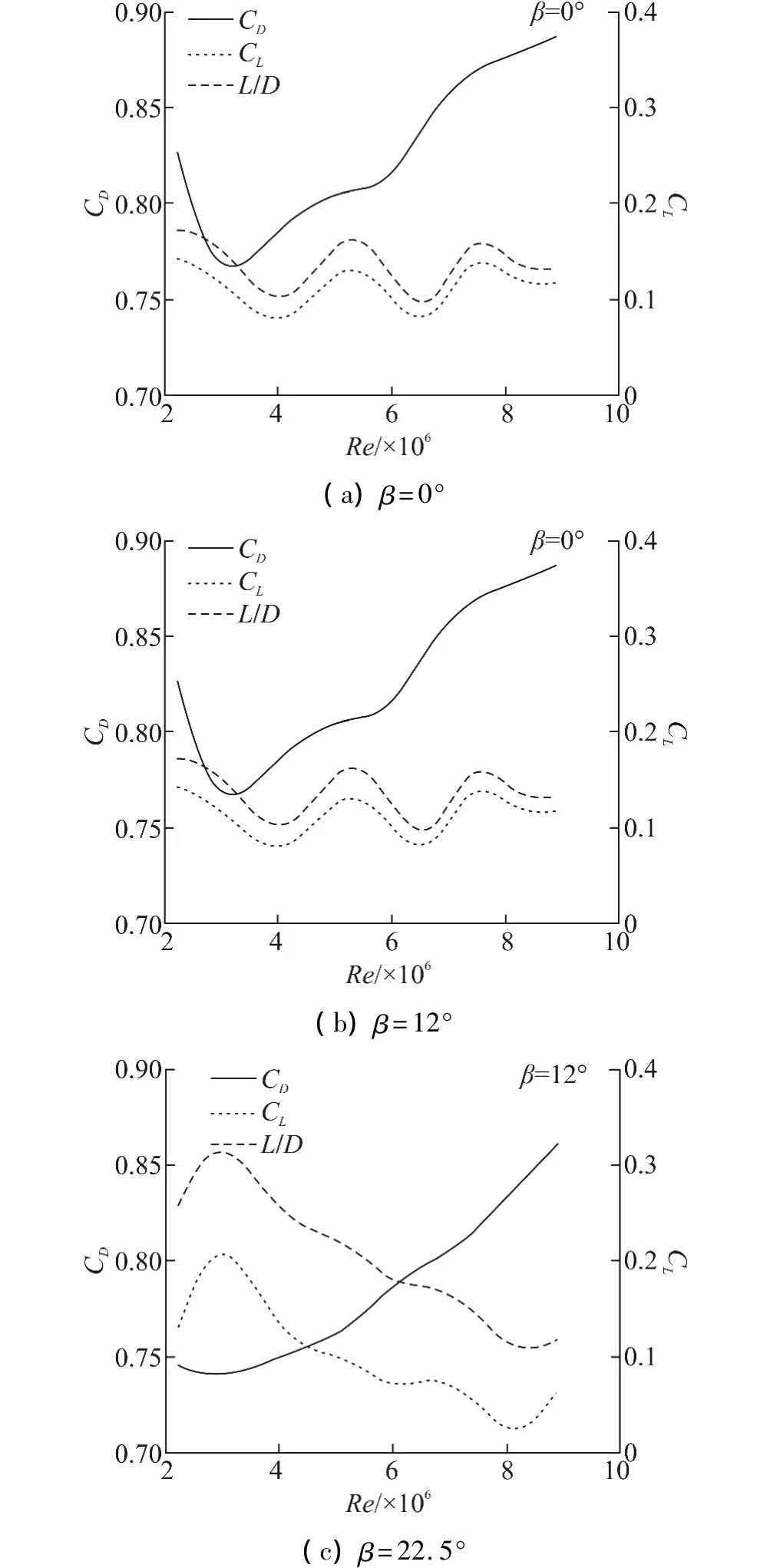
图8 Re数对CD、CL和L/D数的影响Fig.8 Influence of Re number on CD，CLand L/D

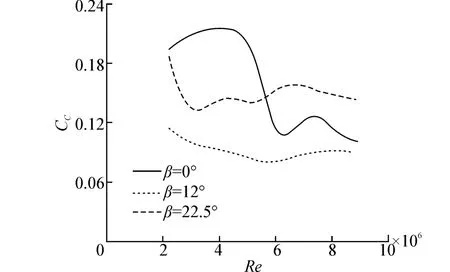
图9 Re数对侧力系数CC的影响Fig.9 Influence of Re number on side force coefficient CC

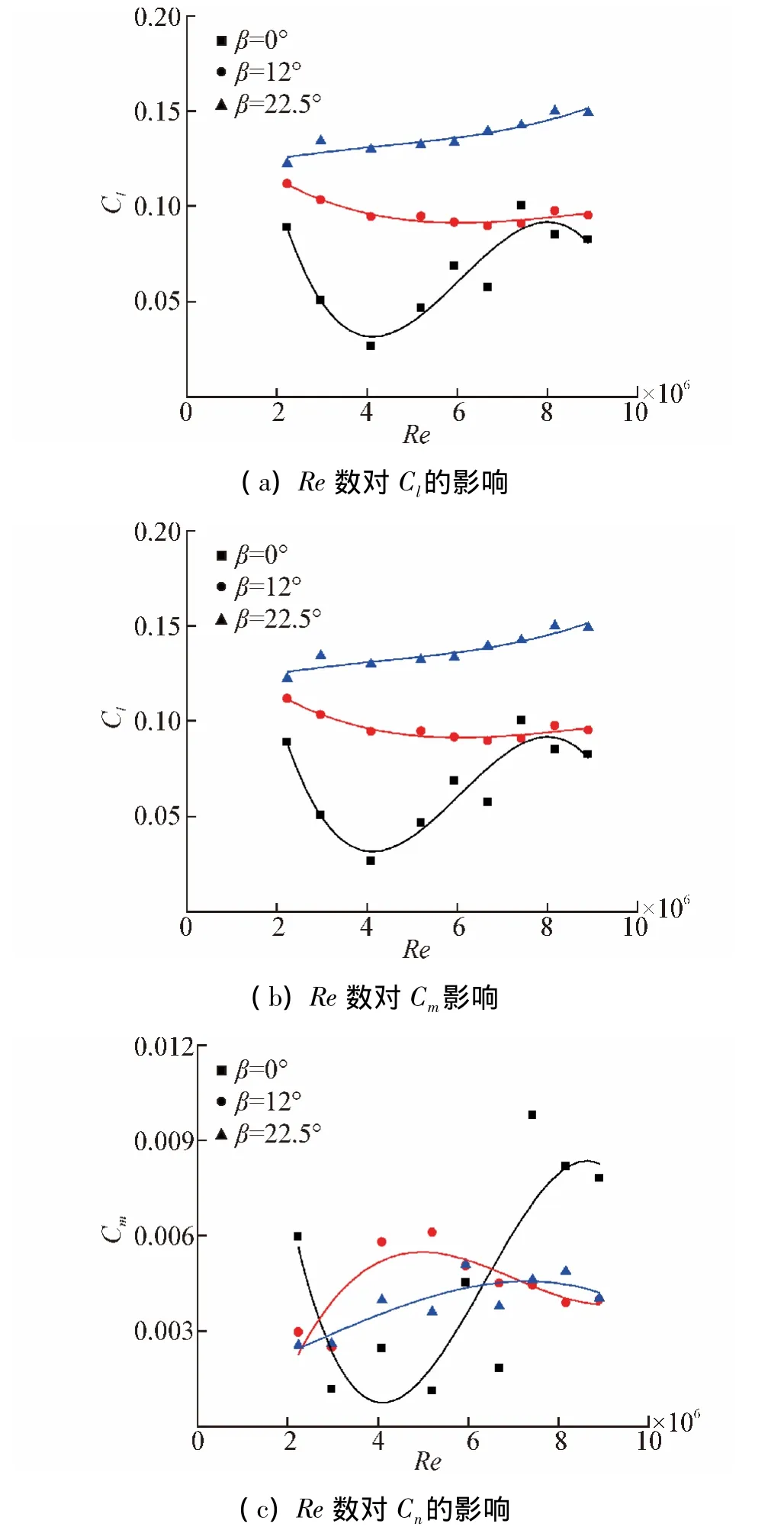
图10 Re数对定常力矩系数的影响Fig.10 Influence of Re number on constant-moment coefficient

分析可知:

1)不同风向角下的滚转力矩系数随Re数的变化趋势差别较大，β=0°下Cl先降低后升高，且幅值高达0.06，相比之下β=12°和β=22.5°对应的曲线变化幅值较小，且趋势基本相反，前者表现为微幅下降，后者则为小幅上升;

2)同β=0°对应的滚转力矩系数的变化趋势类似，β=0°下俯仰力矩系数整体表现为随Re数的升高，先降低后升高，而β=12°和β=22.5°的俯仰力矩系数变化趋势相似，均呈现出缓慢增长再降低，但前者幅值较大;

3)在3个风向角下Re数对偏航力矩系数的影响基本相同，整体上均随Re数的增大而升高，且上升斜率相差不大，在范围内基本维持在0.35～0.42。

2.7 风向角β对阻力系数CD的影响

阻力系数CD随风向角β的变化曲线如图11所示，可知，随着风向角从0°到22.5°变化，阻力系数有先降低后升高的趋势，但升降幅值随Re数的增加而逐渐减小，通过对比不同风向角下周向平均压力系数分布(图5)，原因可能是风向角的改变使结构迎流面和边界层分离区域发生偏移，同时结构外形对后者的影响也较大，而对背流区的影响相对有限，风向角β=0°和β=22.5°时对应的流场对称分布，在边界层分离点后方均有一对强度相当、影响范围较广的峰值，而β=12°对应的流场为非对称分布，存在的2个压力峰值同样非对称分布，且峰值衰减较快，影响范围相对较窄，导致对称分布流场对应的阻力系数略高于非对称分布流场情况。

图11 风向角β对阻力系数CD的影响Fig.11 Influence of wind direction β on drag coefficient CD

3 结论

通过开展风洞试验研究了变截面正八边形结构在2.2242×106≤Re≤8.8969×106范围内的绕流特性，分析了周向平均压力系数的分布特点及其受Re数、风向角、倾角的影响，同时还分析了Re数对气动力系数的影响，得到如下结论:

1)正八边形结构的周向平均压力系数变化较大，且试验范围内Re数变化主要影响边界层的分离强度，当Re＞5×10，Re数对周向压力分布影响很小;风向角对周向平均压力系数的影响体现在对迎流面驻点和边界层分离点附近压力分布的影响，但对于背流面影响有限，基本保持稳定;而倾角仅影响结构两侧边界层分离点附近压力分布，且与风向角有较大的关联性。

2)Re数对升力系数和阻力系数的影响规律与风向角的关联较为密切，同时阻力系数与升阻比表现出高度的一致性，而风向角对阻力系数的影响整体表现为先减小后增大的趋势，且随Re数的增大阻力系数的升降幅值渐降;在试验Re数范围内3个风向角下侧力系数表现出不同幅值的先降低后波动稳定的趋势，主要是受结构周向风载垂向分量与上表面压力综合作用的影响。

3)滚转力矩系数、俯仰力矩系数和偏航力矩系数与Re数的关系类似气动力系数与Re数关系，整体呈现出与风向角较大的关联性。

［1］MOURITZ A P，GELLERT E，BURCHILL P，et al.Review of advanced composite structures for naval ships and submarines［J］.Composite Structures，2001，53(1):21-42.

［2］黎南.国外舰船隐身技术的发展动向与分析［J］.舰船电子工程，2013，33(4):15-17.

LI Nan.Development trend and analysis of the foreign naval ship stealth technology［J］.Ship Electronic Engineering，2013，33(4):15-17.

［3］王世安.水面舰船隐身技术的发展动向与分析［J］.舰船电子工程，2014，34(3):16-20.

WANG Shi＇an.Development trend and analysis of the stealth technology for surface ship［J］.Ship Electronic Engineering，2014，34(3):16-20.

［4］李秋胜，李慧真，李毅.椭圆形高耸结构风荷载特性试验研究［J］.湖南大学学报:自然科学版，2015，42(1): 1-8.

LI Qiusheng，LI Huizhen，LI Yi.Experimental study of the characteristics of wind loads on an oval-shaped high-rise structure［J］.Journal of Hunan University:Natural Sciences，2015，42(1):1-8.

［5］YOON D H，YANG K S，CHOI C B.Flow past a square cylinder with an angle of incidence［J］.Physics of Fluids，2010，22(4):043603.

［6］WANG Wen，HUAI Wenxin，GAO Meng.Numerical investigation of flow through vegetated multi-stage compound channel［J］.Journal of Hydrodynamics，2014，26(3): 467-473.

［7］吴小翠，王一伟，黄晨光，等.飞艇大攻角绕流气动特性模拟及湍流模型与参数影响研究［J］.工程力学，2014，31(8):24-31，69.

WU Xiaocui，WANG Yiwei，HUANG Chenguang，et al.Aerodynamic simulation of airship ambient flows with high attack angles and analysis on turbulence models and parameters［J］.Engineering Mechanics，2014，31(8):24-31，69.

［8］田中伟.正多边形绕流问题研究［D］.北京:清华大学，2010:20-59.

TIAN Zhongwei.A study on flow past regular polygons［D］.Beijing:Tsinghua University，2010:20-59.

［9］刘天成，葛耀君，曹丰产，等.基于Lattice Boltzmann方法的方柱绕流模拟［J］.同济大学学报:自然科学版，2008，36(8):1028-1033.

LIU Tiancheng，GE Yaojun，CAO Fengchan，et al.Simulation of flow around square cylinder based on Lattice Boltzmann Method［J］.Journal of Tongji University:Natural Science，2008，36(8):1028-1033.

［10］AGRAWAL A，DJENIDI L，ANTONIA R A.Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method［J］.Computers and Fluids，2006，35(10):1093-1107.

［11］唐鹏，韩省思，叶桃红，等.联合RANS/LES方法数值模拟方柱绕流［J］.中国科学技术大学学报，2010，40 (12):1287-1292.

TANG Peng，HAN Shengsi，YE Taohong，et al.Hybrid RANS/LES simulation of flow past a square cylinder［J］.Journal of University of Science and Technology of China，2010，40(12):1287-1292.

［12］DING H，SHU C，YEO K S，et al.Numerical simulation of flows around two circular cylinders by mesh-free least square-based finite difference methods［J］.International Journal for Numerical Methods in Fluids，2007，53(2): 305-332.

［13］LAM K，LIN Y F，ZOU L，et al.Investigation of turbulent flow past a yawed wavy cylinder［J］.Journal of Fluids and Structures，2010，26(7-8):1078-1097.

［14］LAM K，LIN Y F，ZOU L，et al.Numerical simulation of flows around two unyawed and yawed wavy cylinders in tandem arrangement［J］.Journal of Fluids and Structures，2012，28:135-151.

［15］VAKIL A，GREEN S I.Drag and lift coefficients of inclined finite circular cylinders at moderate Reynolds numbers［J］.Computers＆Fluids，2009，38(9):1771-1781.

［16］姚熊亮，康庄，张洪雨，等.五边形筒型桅杆模拟风载试验研究［J］.水动力学研究与进展，2004，19(5): 648-654.

YAO Xiongliang，KANG Zhuang，ZHANG Hongyu，et al.Experimental research of the wind loads on pentagonal stealth mast［J］.Journal of Hydrodynamics，2004，19 (5):648-654.

［17］姚熊亮，张凌江，曾令玉，等.封闭式综合集成桅杆风载特性实验研究［J］.振动与冲击，2009，28(11):51-54.

YAO Xiongliang，ZHANG Lingjiang，ZENG Lingyu，et al.Experimental research on wind-load characteristics of integrated mast［J］.Journal of Vibration and Shock，2009，28 (11):51-54.