基于快速多极子的舰船感应磁场快速预报方法

周国华，刘胜道，肖昌汉，刘大明

(海军工程大学电气工程学院，湖北武汉430033)

钢铁结构舰船周围存在的磁异常信号是水中磁性兵器攻击和空中磁性探测的重要信号源。为了提高舰船生命力，各国海军都在致力于研究舰船磁性防护方法及措施，其中重点研究内容之一就是舰船受地磁场磁化作用产生的感应磁场数值建模及其防护问题［1-4］。

鉴于磁场积分法只需剖分源区、易于处理开域问题等优点，常被应用于舰船感应磁场计算领域［5-7］。舰船三维复杂结构使得舰船感应磁场数值计算中需较多的剖分单元才能获得相对稳定精确的计算结果。然而由于磁场积分法系数矩阵为非对称稠密阵，基于磁场积分法的船磁计算时间随舰船剖分单元数目的增加而快速增长，从而使得过去舰船感应磁场建模大多停留于小规模计算［2-4］，影响了船磁计算效率及磁场积分法在船磁计算领域的推广应用。20世纪末期，Rokhlin和Greengard创造性地提出了加速矩阵与向量乘积运算的快速多极子方法(fast multipole method，FMM)［8-9］。随着快速多极技术的不断发展，求解大规模问题的快速计算优势逐渐被进一步开发，目前已被广泛应用于电磁散射、弹性位势、声学技术等领域［10-12］。

为提高船磁积分方程计算效率，本文将快速多极子技术与磁场积分法相耦合，提出了基于快速多极子和积分方程的舰船感应磁场快速预报方法，设计了球体感应磁场解析算例和地磁作用下简化艇模主舱段感应磁场实验。

1 磁场积分法

如图1所示，在外磁场B0作用下的铁磁物体(如铁质舰船)在空间点P产生的磁感应强度可表示为［13］

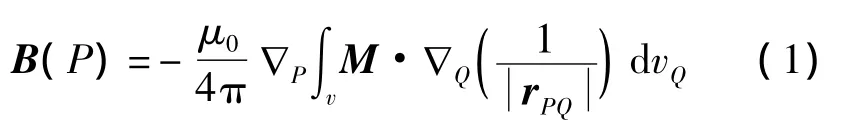
式中:▽P为对场点坐标的梯度算子，▽Q为对源点坐标的梯度算子，v为铁磁物体所占体积，M为由外磁场磁化引起的铁磁物体内部磁化强度，P为场点，Q为源点。

图1 静磁计算问题示意图Fig.1 The sketch map of magnetostatic computation

对于均匀磁化体，式(1)中体积分可简化为面积分

式中:s为均匀磁化体表面积，n为均匀磁化体表面外法线方向。

为得到铁磁物体内部的磁化强度，通常将铁磁物体离散为若干足够小的均匀磁化体。以每个离散单元中心为计算场点，可建立以单元内部磁感应强度为未知量的代数方程组

式中:j=1，2，…，N，N为铁磁物体离散单元数，μri为第i个单元内部的相对磁导率。采用矩阵形式可表示为

其中:C为系数矩阵并由式(3)决定，X为铁磁物体各离散单元内部磁感应强度组成的向量，Y为铁磁物体各离散单元中心处外加磁场组成的向量。求解方程组(4)即可得到铁磁物体内部磁感应强度分布，再根据单元内部场量关系M=(μr－1)B/(μ0μr)及式(1)即可求得空间任意点P的磁感应强度值。上述即为用于舰船感应磁场计算的基于磁感应强度B的磁场积分法的基本原理。

采用上述磁场积分法求解外磁场作用下的铁磁物体磁化场问题时，形成的系数矩阵为非对称稠密阵，当剖分单元N较大时，迭代求解代数方程组(4)将消耗大量的时间，大大影响了计算效率。本文提出了基于快速多极子和磁场积分法的舰船感应磁场快速预报方法，以改善舰船感应磁场计算效率。

2 快速多极子加速磁场积分算法

快速多极子技术的核心思想是将积分方程核函数展开成2个分别仅与源点和场点有关的函数，再通过聚合、转移和发散过程来减少系数矩阵每次迭代的计算量，从而提高计算速度。快速多极子加速积分方程计算过程是建立在上述磁场积分法和线性代数方程组迭代法求解基础上的。如图2所示(为直观清晰，采用四叉树结构绘图)，该方法先将铁磁区进行离散，然后用一个立方体将所有离散单元罩住，并将其等分为8个子立方体，依次类推直至最小立方体包含的离散单元数目至多Nmax个为止，这样就得到了罩住所有离散单元的一批立方体，按照相应规则即可建立对应八叉树。

对于某个参考立方体boxj而言，其他立方体又被区分为近距立方体和远距立方体。每个立方体内及近距立方体内离散单元间的相互作用仍采用磁场积分法直接进行计算，而大量远距立方体内离散单元间的作用通过聚合、转移、发散的快速多极算法来实现。因而，这就避免了显式地产生积分方程系数矩阵，且加速了迭代法求解代数方程中矩阵向量乘积运算。

图2 用四叉树表示的立方体关系示意图Fig.2 The relationship ofcubicsdipicted with quadtree

2.1 积分核函数多极展开

为适应三维复杂舰船的剖分，采用非规则六面体单元。当剖分单元数目足够多时，可将每个离散单元磁场强度矢量B视为常量，被积函数中各物理量之间关系如图3所示。

图3 被积函数中各物理量之间关系图Fig.3 The relationship of each symbol in integral function

为便于加速计算，根据快速多极子理论，需将式(2)被积函数中Green函数的基本解用双谐函数进行展开［14］:

式中:rP为场点P的矢径，rQ为源点Q的矢径，n为多极子展开阶数，取值影响着计算精度和计算速度; Rn，m和Sn，m分别为球面调和函数表示Sn，m的共轭复数，不同应用领域其定义略有不同，此处定义为

式中:(ρ，α，β)和(r，θ，φ)分别为rQ和rP的球坐标，为连带勒让德函数，其定义为

其中，Pn为勒让德函数，且连带勒让德函数满足:

将式(2)采用式(5)展开，经推导不难得到

其中

式(13)称为以O点为中心的源点矩或多极子展开公式(multipole expansion，ME)。

2.2 源点矩到本地展开系数的转变

当|OPO|＞|POP|，有球面调和函数关系式［15］:

代入以O为中心的展开式(12)，经推导可得:

其中

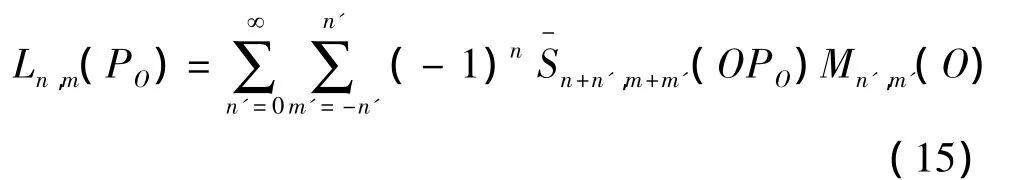
式(15)称为将以O为中心的源点矩转变为以PO为中心的展开系数的传递公式(moment to local translation，M2L)。

2.3 本地展开系数转移

基于式(14)可将本地展开系数发散至场点P (local expansion，LE)，实现相应单元之间贡献量的计算，简写成:

在利用快速多极子加速磁场积分法计算中，源区单元对场区单元的聚合、转移和发散等过程如图4所示。

图4 聚合、转移、发散等过程示意图Fig.4 The sketch map of ME，M2L and LE

2.4 算法基本步骤

采用快速多极子加速积分方程求解三维静磁问题具体步骤如下:

1)网格剖分。对计算对象进行离散剖分，以获取单元信息和节点信息。目前可用来进行网格剖分的软件较多，为提高效率，本文不独立编写剖分程序而直接选用TrueGrid软件来进行剖分。鉴于非规则六面体单元具有剖分通用性强等优点，因而将其作为计算对象网格模型的基本单元。

2)建立八叉树。将整个计算对象用一个足够大的立方体罩住;将该立方体分为8个子立方体，每个立方体再分为8个更小的子立方体，依次类推直到所需层数，该层满足每个子立方体包含的单元数不超过给定的数目Nmax。按照要求将该层立方体编号并建立描述立方体相互关系的近距组、远距组信息数组［14］，如第i个立方体内部单元数numt(i)、第i个立方体父立方体的编号ifath(i)、第i个立方体在本层中的编码itree(i)、第i个立方体开始的单元个数编号loct(i)、单元原始编号在八叉树结构中的编码ielem(i)等。

3)采用Gmres迭代法求解方程组(4)。迭代过程中涉及大量C3N×3NX3N矩阵向量乘积运算，但采用快速多极子与积分方程相耦合可大大加速矩阵向量乘积运算，具体步骤如下:

①初始化迭代参数、快速多极子参数;

②将各单元作用聚合到每个相应立方体中心，即按式(13)计算源点矩;

③按照原始积分式(3)直接计算自身立方体内及近距立方体内单元之间的相互作用;

④采用快速多极算法计算远距立方体内单元之间的相互作用，以boxj为例，根据式(15)将其任一远距立方体boxi的源点矩转移到自身立方体boxj中心，根据式(16)将以boxj为中心的展开系数发散至自身立方体内每一个单元中心，通过这一过程即实现了boxi内所有单元到boxj内所有单元贡献系数的计算;

⑤将上述2部分贡献量相加即可实现式(4)中的矩阵矢量相乘，可以写为

式中:w1为包含在叶子立方体内自身及其近距立方体内的源点单元，w2为包含在远距立方体内源点单元。等式右边第1项表示w1中的单元对第j个单元贡献量，采用磁场积分法直接计算;等式右边第2项表示w2中的单元对第j个单元贡献量，采用快速多极算法加速计算。

⑥根据Gmres迭代算法更新每个单元内部磁感应强度，判别误差要求，若不满足迭代结束条件，返回②重新迭代计算。

2.5 编程流程及数值实现的注意点

为提高代码执行效率，基于快速多极子和磁场积分法的船磁计算软件源代码采用Fortran90编写，在Intel Visual Fortran编译环境下调试运行。计算硬件选用8核3.4GHz CPU和4GB RAM台式计算机，操作系统为32位Windows XP。算法实现流程如图5所示。

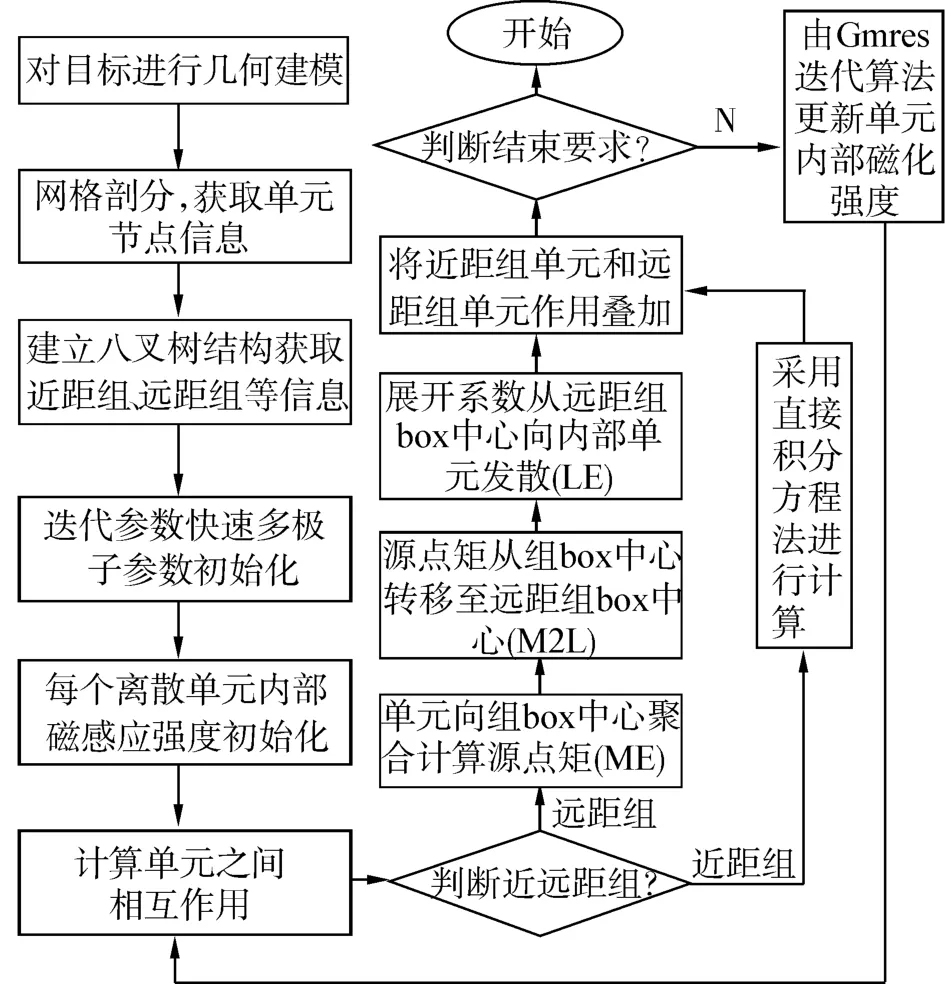
图5 快速多极子加速积分方程计算流程图Fig.5 The flow chart of fast multipole method and integral equation method

3 计算实例

3.1 均匀外场作用下铁质球体感应磁场解析算例

采用均匀外磁场作用下铁质球体产生的感应磁场，验证所提出算法及程序的正确性。

如图6所示，半径为10 m、相对磁导率为150的铁质球体放置于均匀外磁场B=［34 500 0 0］中。铁质球体受外磁场磁化在其周围产生的感应磁场可解析求得［16］，将其作为用于数值模拟比较的理论值。61个计算场点沿x轴方向关于原点对称均匀分布在球体下方、间距0.5 m、距球体中心高度15 m。

图6 均匀地磁场作用下铁质球体剖分Fig.6 The mesh of the iron sphere submerged in an applied magnetic field

为考核基于快速多极子和磁场积分法的船磁快速算法的计算效率及所编程序正确性，分别将该铁质球体剖分为729、1 331、1 728、2 197、3 375个非规则六面体单元。在上述5种剖分条件下，分别采用直接磁场积分法(DIEM)［16］和采用快速多极子加速积分方程快速算法(本文方法)来计算场点处感应磁场。本文方法算法中单个立方体包含的最大单元数Nmax取，其中EleNum为单元个数。迭代参数设置为:迭代结束相对残差取10－8，最大迭代次数50。

图7给出了采用2种数值模拟方法所求得感应磁场与理论值的对比曲线，其中Theory、DIEM、本文方法分别表示由解析方法、直接磁场积分法和采用快速多极子加速积分方程求得的感应磁场，Bx、By和Bz分别表示球体感应磁场的X分量、Y分量和Z分量。由图7结果表明，与感应磁场理论值相比，本文方法和DIEM计算的最大相对误差分别为0.63%和0.49%，均可实现高精度计算。图中局部放大处表明本文方法的计算误差略大于DIEM，主要是由于远区单元之间作用近似计算所致。图8给出了2种数值模拟方法求解场点感应磁场计算时间比较曲线。

图7 球体感应磁场计算值与理论值比较图Fig.7 The comparison of the calculated and the theory induced magnetic field of the iron sphere

图8 2种数值模拟方法计算时间比较曲线Fig.8 The comparison of the computation time of the two numerical methods

由图8可以看出，本文方法计算效率远高于DIEM，随着剖分单元个数的增加，本文方法方法计算效率优势越来越明显。上述计算结果表明了采用快速多极子加速积分方程快速算法所编程序正确性。

3.2 简化艇模主舱段感应磁场实验算例

为方便，采用地磁场作用下简化艇模主舱段产生的感应磁场，验证所提出算法的工程实用性。

如图9所示，相对磁导率155的简化艇模主舱段，置于均匀地磁场中，地磁场水平分量和垂直分量分别为34 500 nT和34 800 nT。计算场点沿z轴方向关于原点对称均匀分布于简化艇模主舱段下方，纵向间距100 mm、横向间距200 mm、垂向距离358 mm。

图9 地磁场作用下简化艇模主舱段剖分Fig.9 The mesh of the main cabin of the simple submarine mockup submerged in an applied magnetic field

为消除简化艇模主舱段剩磁对考核数值模拟误差的影响，利用测磁精度为1 nT的多通道测磁系统在地磁北向和南向分别测量得到了简化艇模主舱段产生的磁感应强度，并根据所测得的数据分解出简化艇模主舱段受地磁场水平磁化作用而在场点产生的磁感应强度值［2］，将其作为数值模拟的比对值。

将简化艇模主舱段剖分为8 160个非规则六面体单元，单个立方体包含的最大单元数 Nmax取迭代参数设置与计算实例1相同。

采用本文方法来计算简化艇模主舱段感应磁场共耗时214 s。图10给出了简化艇模主舱段受地磁场水平分量磁化作用而产生的感应磁场测量值与计算值对比曲线。

图10 简化艇模主舱段受地磁场水平分量磁化作用而产生的感应磁场测量值与计算值对比曲线图Fig.10 The comparison of the calculated and the measured induced magnetic field of the simple submarine mockup magneitzed by horizontal geomagnetic field

由图10可以看出，测量值与计算值吻合很好，最大相对误差为4.14%，可以满足工程需求。然而，在相同条件下采用直接磁场积分法进行计算时，耗时超过1 h。相比较而言，本文方法可大大提高船磁计算效率。

4 结束语

本文提出了基于磁场积分法和快速多极子的舰船感应磁场快速预报方法，并编制了相应程序包，为解决舰船感应磁场快速计算提供了一条技术途径。解析球体和简化艇模主舱段感应磁场计算实例表明，该方法计算精度高、速度快，具有很高的工程实用价值。与直接磁场积分法相比，在相同计算条件下，当离散单元数目达到3 000时，即可减少计算时间近5倍，随着离散单元数目的增加，该方法加速效果更加显著。值得指出的是，文中采用的是单层快速多极子来加速磁场积分船磁计算过程，若采用多层快速多极子、自适应多层快速多极子等技术效果将更加明显，这也是将来进一步研究的内容。

［1］HOLMES J J.Modeling a ship＇s ferromagnetic signatures［M］.［S.l.］:Morgan and Claypool Publishers，2007:1-4.

［2］郭成豹，刘大明，肖昌汉，等.舰载活动设备磁场建模分析研究［J］.兵工学报，2009，30(2):196-200.

GUO Chengbao，LIU Daming，XIAO Changhan，et al.Magnetic field modelling of shipborne moving equipment［J］.Acta Armamentarii，2009，30(2):196-200.

［3］翁行泰，曹梅芬.潜艇感应磁场的三维有限元法计算研究［J］.上海交通大学学报，1994，28(5):69-76.

WENG Xingtai，CAO Meifen.A research on the calculation of the induced magnetic field of a submarine［J］.Journal of Shanghai Jiaotong University，1994，28(5):69-76.

［4］陈杰，鲁习文.舰船感应磁场预测的一种新方法［J］.物理学报，2010，59(1):239-245.

CHEN Jie，LU Xiwen.A new method for predicting the induced magnetic field of naval vessels［J］.Acta Physica Sinica，2010，59(1):239-245.

［5］CHADEBEC O，COULOMB J L，LECONTE V，et al.Modeling of static magnetic anomaly created by iron plates［J］.IEEE Transactions on Magnetics，2000，36(4):667-671.

［6］郭成豹，何明，周耀忠.积分方程法计算舰船感应磁场［J］.海军工程大学学报，2001，13(6):71-74.

GUO Chengbao，HE Ming，ZHOU Yaozhong.Calculation of induced magnetic fields of ships by integral equation method［J］.Journal of Naval University of Engineering，2001，13 (6):71-74.

［7］周国华，肖昌汉，闫辉，等.一种弱磁作用下铁磁物体感应磁场的计算方法［J］.哈尔滨工程大学学报，2009，30 (1):91-95.

ZHOU Guohua，XIAO Changhan，YAN Hui，et al.A method to calculate the induced magnetic field of ferromagnetic objects in a weak magnetic field［J］.Journal of Harbin Engineering University，2009，30(1):91-95.

［8］ROKHLIN V.Rapid solution of integral equations of classical potential theory［J］.Journal of Computational Physics，1985，60(2):187-207.

［9］GREENGARD L，ROKHLIN V.A fast algorithm for particle simulations［J］.Journal of Computational Physics，1987，73(2):325-348.

［10］聂在平，胡俊，姚海英，等.用于复杂目标三维矢量散射分析的快速多极子方法［J］.电子学报，1999，27 (6):104-109.

NIE Zaiping，HU Jun，YAO Haiying，et al.The fast multipole methods for vector analysis of scattering from 3-dimensional objects with complex structure［J］.Acta Electronica Sinica，1999，27(6):104-109.

［11］宁德志，滕斌，勾莹.快速多极子展开技术在高阶边界元方法中的实现［J］.计算力学学报，2005，22(6): 700-704.

NING Dezhi，TENG Bin，GOU Ying.Implementation of the fast multipole expansion technique in the higher order BEM［J］.Chinese Journal of Computational Mechanics，2005，22(6):700-704.

［12］吴海军，蒋伟康，鲁文波.三维声学多层快速多极子边界元及其应用［J］.物理学报，2012，61(5):054301.

WU Haijun，JIANG Weikang，LU Wenbo.Multilevel fast multipole boundary element method for 3D acoustic problems and its applications［J］.Acta Physica Sinica，2012，61(5):054301.

［13］樊明武，颜威利.电磁场积分方程法［M］.北京:机械工业出版社，1988:11-19.

［14］LIU Yijun.Fast multipole boundary element method theory and applications in engineering［M］.New York:Cambridge University Press，2009:71-73.

［15］YOSHIDA K.Applications of fast multipole method to boundary integral equation method［M］.［S.l.］:Kyoto University Press，2001:106-108.

［16］周国华，肖昌汉，刘胜道，等.基于六面体单元表面磁场积分法求解三维静磁场［J］.电工技术学报，2009，24(3):1-7.

ZHOU Guohua，XIAO Changhan，LIU Shengdao，et al.3D magnetostatic field computation with hexahedral surface integral equation method［J］.Transactions of China Electrotechnical Society，2009，24(3):1-7.

［17］盛新庆.计算电磁学要论［M］.北京:科学出版社，2004:29-31.