避让工况下的路径跟踪线性自抗扰控制

王健，赵又群，杨君，钟兵，臧利国

(1.山东交通学院汽车工程学院，山东济南250357;2.南京航空航天大学能源与动力学院，江苏南京210016)

近年来，高速公路交通事故居高不下，其中车辆追尾引发的事故占75%以上［1-2］。高速紧急避让技术能够减少追尾事故的发生率，提高汽车的主动安全性［3］。汽车高速紧急避让系统利用现代信息技术和传感器技术(毫米波雷达、激光雷达、高速摄像机)，将外界信息(当前车辆与前方障碍物之间相对速度、距离等)传递给控制单元，紧急情况下自动采取措施控制车辆，使车辆主动避让前方障碍物，保证车辆行驶安全［4-5］。

高速紧急避让工况下，控制单元发出指令通过执行机构(电动助力转向系统EPS)控制前轮转角完成车辆避让过程。国内外学者采用PID控制、最优控制、鲁棒控制等方法控制车辆前轮完成自动转向过程［6-7］。虽然PID控制简单，但是当车辆参数、转动惯量和轮胎侧偏刚度发生变化时的鲁棒性不强;最优控制和鲁棒控制算法复杂，不利于工程应用，且算法的控制效果很大程度上依赖于被控对象模型的精度［8-10］。

线性自抗扰控制算法发挥了传统PID控制的优点，不依赖于被控对象精确的数学模型，能够将模型参数变化观测和补偿掉，保证系统鲁棒性。线性自抗扰相比于非线性自抗扰控制，需要调整的参数更少，结构更加简单，现在已经成功应用于飞行器控制、船舶控制、机器人控制和导弹控制领域。

1 车辆动力学模型及路径规划

1.1 车辆动力学模型

车辆二自由度动力学方程能够较为准确地反映车辆的横向动力学特性［11-12］。利用二自由度车辆模型，设计线性自抗扰路径跟踪控制器。忽略转向系统的影响，直接以前轮转角作为输入;忽略悬架的作用，忽略路面不平和空气阻力影响。

车辆二自由度动力学状态方程可以表示为

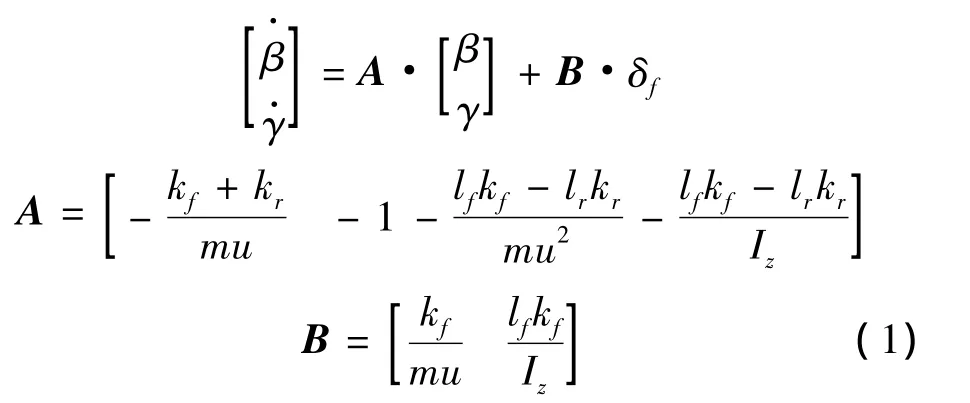
式中:m为车辆质量，Iz为车辆横摆转动惯量，lf、lr为车辆质心到前后轴的距离，kf、kr为前后轮侧偏刚度，u为质心处纵向速度，β为车辆质心侧偏角，γ为车辆质心横摆角速度，δf为前轮转角。

将车辆二自由度动力学状态方程进行拉普拉斯变化，得到横摆角速度与前轮转角之间的传递函数公式为

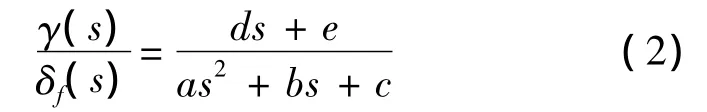
1.2 路径规划

本文采用 Sigmoid曲线进行紧急避让路径规划［15］。其中，避让路径曲线如图1所示。

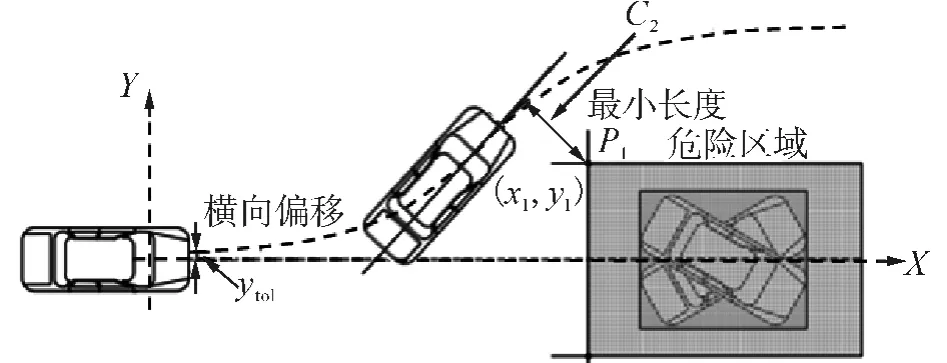
图1 避让路径Fig.1 Predefined path

考虑避让过程约束条件，设计紧急避让路径曲线，其中Sigmoid曲线表达式为

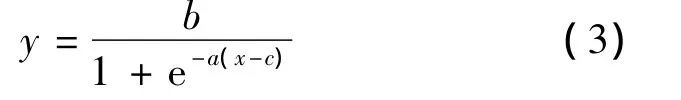
式中:a、b、c是曲线的3个参数量，x表示在全局坐标系下车辆纵向位移，y表示车辆侧向位移。参数(a，b，c)可以通过求解约束方程得到。

约束1:最小长度约束。

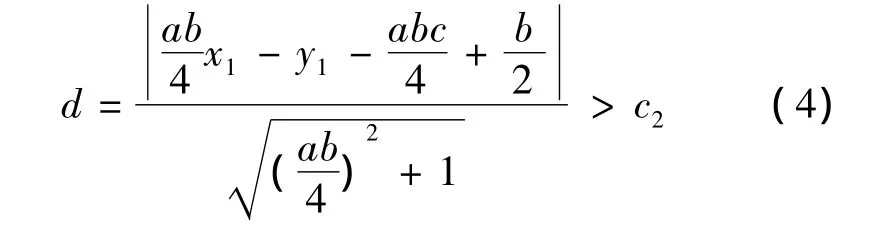
式中:(x1，y1)为P1点的坐标，c2为安全距离。

约束2:起始点车辆侧向位移偏差 (lateral offset)约束。

式中:ytol为起始点车辆侧向位移偏差。

约束3:最大侧向加速度约束。

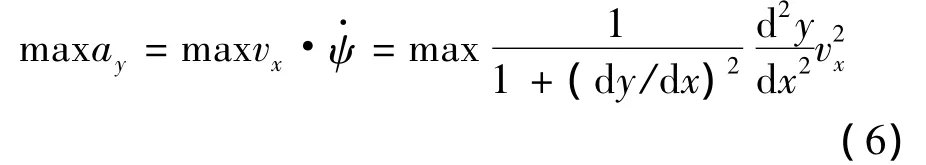
式中:ay为车辆侧向加速度，vx为车辆质心处纵向速度，ψ为车身偏航角度。此处限制侧向加速度最大值ay= 0.67μmg，其中μm为路面附着系数，g为重力加速度［13］。

2 线性自抗扰控制器设计

对式(2)进行拉普拉斯逆变换得

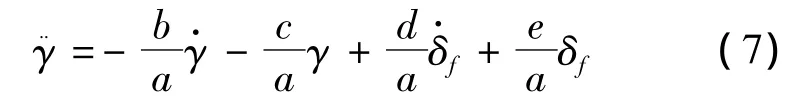
方程(7)可以化成积分串联型系统，即标准形式:

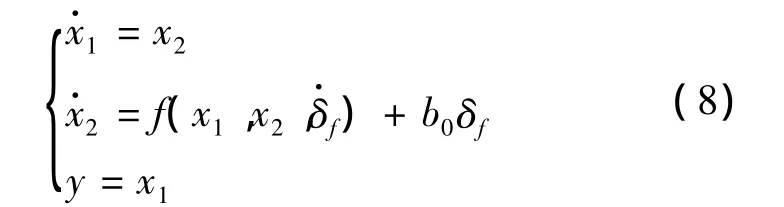
2.1 线性跟踪微分器

线性自抗扰控制器由线性跟踪微分器(LTD)、线性组合(LSEF)、线性扩张状态观测器(LESO)3部分组成。LTD取代传统PID的微分环节，解决了传统PID跟踪快速性与超调之间的矛盾，避免了控制输入信号快速波动问题［9］。LTD离散化形式为

其中:γd(k)表示目标输入信号，h表示仿真步长，k为第k次采样，v1(k)和v2(k)分别跟踪γd(k)和(k)，k1和k2为设计参数。

2.2 线性扩张状态观测器

线性扩张状态观测器(LESO)将模型不确定性及外界干扰看作一个整体扰动量，通过扩张的状态观测器将这个总的扰动量观测出来。二阶线性自抗扰控制器利用三阶LESO进行干扰量的观测，其中，三阶LESO的离散表达式可以描述成:

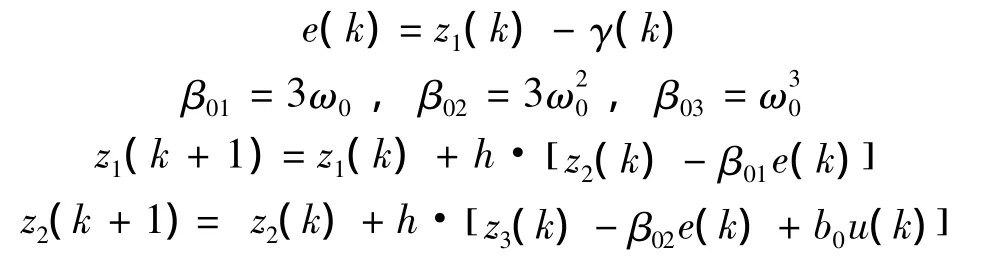
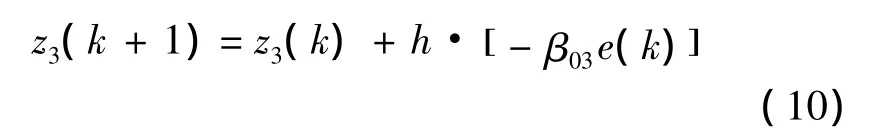
式中:γ(k)为被控对象输出，z1(k)、z2(k)和z3(k)代表线性自抗扰控制器的输出，ω0表示LESO的带宽，b0为设计参数。

2.3 线性状态误差反馈控制律

LSEF实际上是一个线性PD控制律，可以用以下离散形式进行描述:

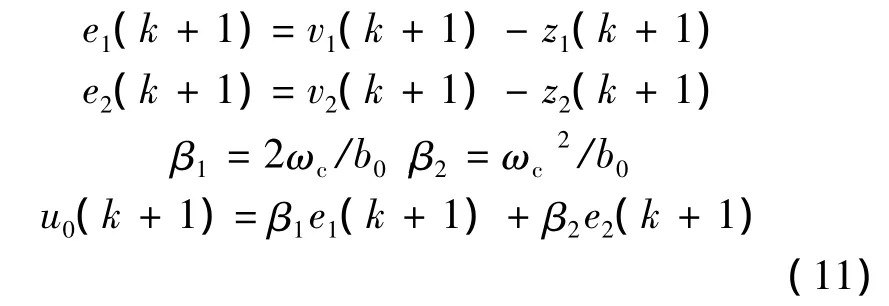
式中:ωc为期望的闭环系统带宽;5ωc≤ω0≤10ωc;β1和β2是设计参数，可以用闭环系统的带宽进行求解。

控制律u0是误差e1和误差的微分e2的线性组合形式。为了消除总的未知干扰，需要在输入被控对象执行机构之前抵消掉这些未知扰动，实际作用在被控对象执行机构的控制量u可以表示为

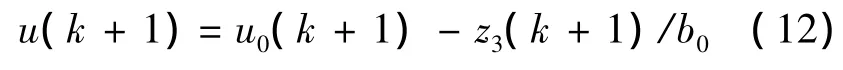
3 联合仿真试验

为了验证本文建立的线性自抗扰路径跟踪控制器的控制效果，进行Carsim和Simulink联合仿真试验［14］。利用Carsim软件提供的某款SUV进行实车仿真试验，其中车辆参数如表1所示。

表1 车辆参数Table 1 Vehicle parameters

当车辆质量、横摆转动惯量和前后轮侧偏刚度发生变化时(变化范围为 ±20%)，验证路径跟踪控制器的鲁棒性。其中车辆纵向速度为30 m/s，路面附着系数为0.8，线性自抗扰控制器参数经过不断调整试验得到:ω0=300，ωc=50，b0=372。

当整车质量发生变化时，车辆横摆转动惯量和前后轮侧偏刚度不变时，车辆实际行驶轨迹与理想规划轨迹对比如图2(a)所示，其中图2(b)为车辆实际横摆角速度跟踪理想横摆角速度情况，从图中可以看出当车辆质量发生变化时，线性自抗扰控制器能够控制车辆实际横摆角速度跟踪理想横摆角速度变化，线性扩张状态观测器能够将模型参数不确定观测出来，如图2(c)所示(无量纲)。

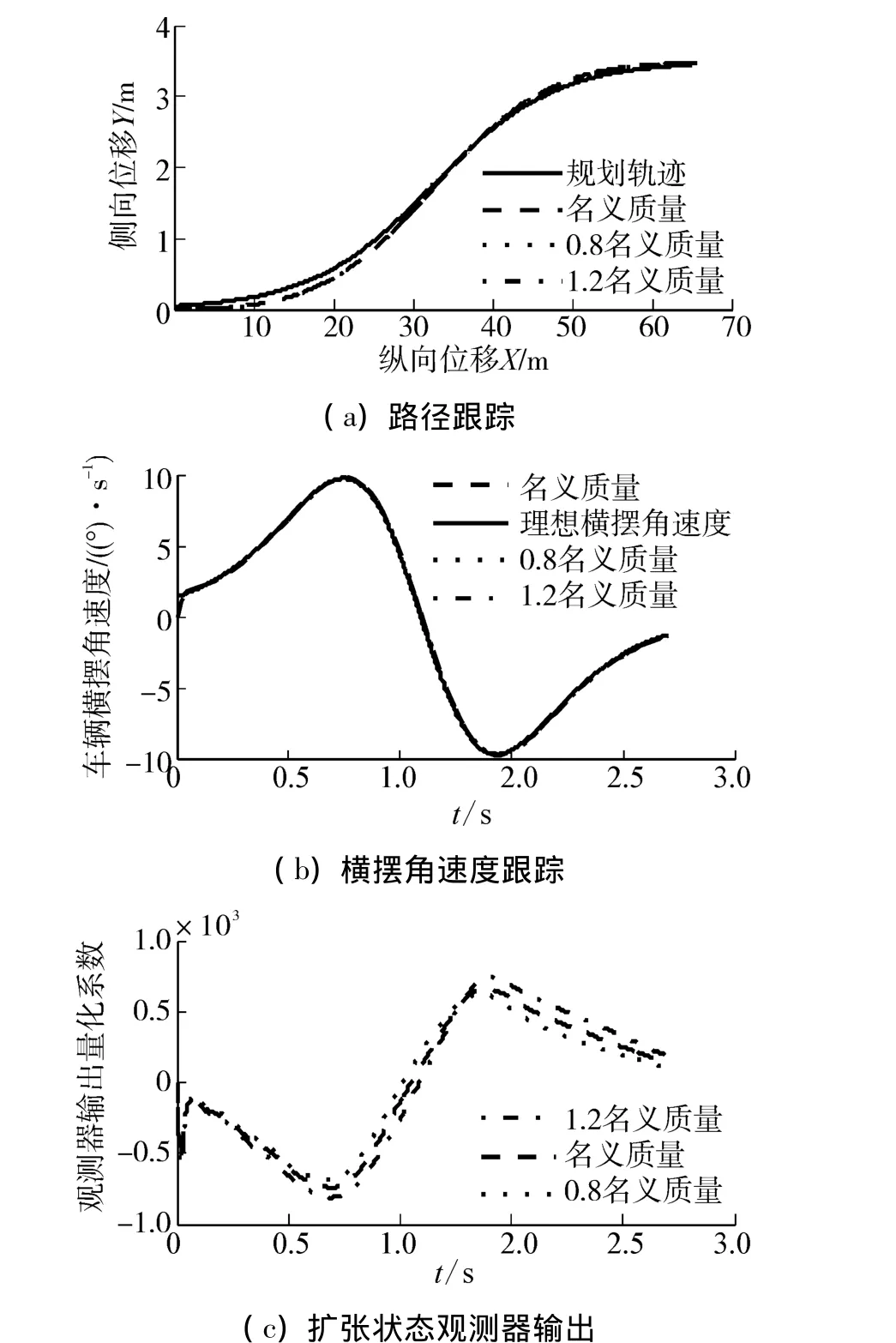
图2 车辆质量变化时控制器输出曲线Fig.2 Output curve of the controller with vehicle quality change

当车辆横摆转动惯量在名义值上下 ±20%变化时，控制器输出曲线如图3所示。其中车辆路径跟踪曲线如图3(a)所示，可以看出车辆实际行驶轨迹能够很好的跟踪规划的轨迹;其中横摆角速度跟踪曲线如图3(b)所示，实际车辆横摆角速度能够很好的跟踪理想横摆角速度变化情况;图3(c)为扩张状态观测器输出的系统受到的“总扰动量”，线性自抗扰控制器通过对系统参数模型不确定性进行观测补偿，保证路径跟踪鲁棒性。当车辆前后轮侧偏刚度在名义值上下 ±20%变化时，控制器输出曲线如图4所示。车辆实际行驶规划与理想规划轨迹对比如图4(a)所示，横摆角速度跟踪如图4(b)所示，线性扩张状态观测器输出如图4(c)所示。

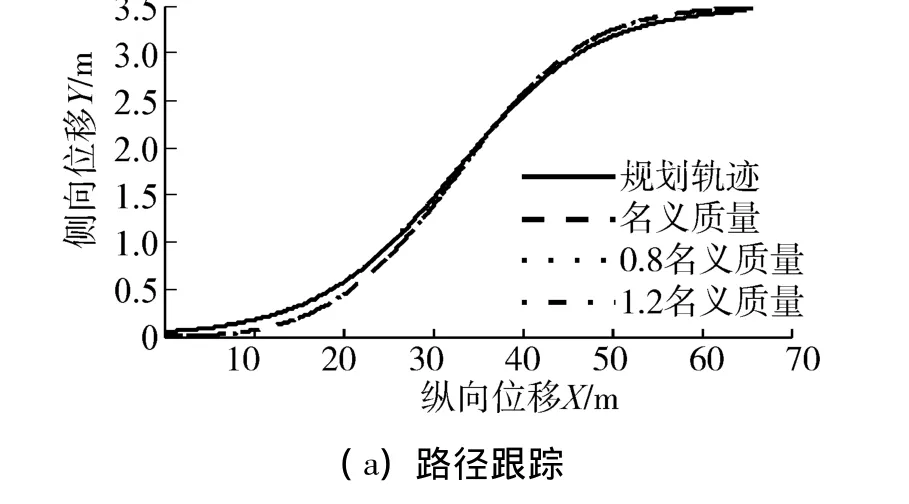
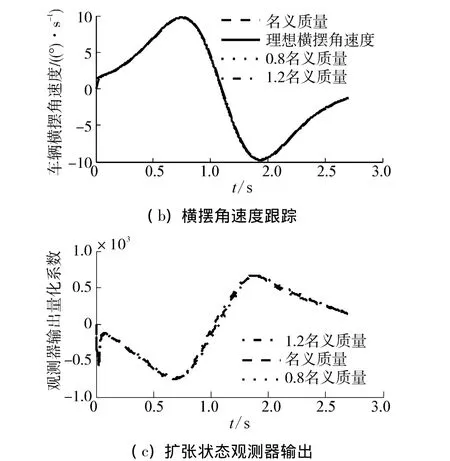
图3 车辆横摆转动惯量变化时控制器输出曲线Fig.3 Output curve of the controller with vehicle yaw moment of inertia

图4 车辆前后轮侧偏刚度变化时控制器输出曲线Fig.4 Output curve of the controller with front and rear wheel side stiffness

通过上述仿真试验发现，车辆在参数发生变化时(车辆质量、横摆转动惯量、前后轮侧偏刚度)，线性自抗扰路径跟踪控制器依然能够控制车辆实际横摆角速度跟踪理想规划横摆角速度，保证车辆实际行驶路径跟踪理想规划路径，同时保证避让过程路径跟踪鲁棒性。

4 结束语

本文以二自由度车辆模型为基础，通过控制车辆实际横摆角速度跟踪理想横摆角速度，设计二阶线性自抗扰路径跟踪控制器，保证车辆实际行驶路径跟踪理想规划路径，方法简单可行。通过Carsim与Simulink联合仿真验证了当车辆质量、横摆转动惯量和前后轮侧偏刚度发生变化时，线性自抗扰路径跟踪控制器能够控制车辆实际横摆角速度跟踪规划的理想横摆角速度变化。线性扩张状态观测器能够将系统受到的“总扰动量”观测出来补偿掉，保证路径跟踪的鲁棒性。

［1］HUANG S，YANG J，EKLUND F.Evaluation of remote pedestrian sensor system based on the analysis of car-pedestrian accident scenarios［J］.Safety Science，2008，46(9): 1345-1355.

［2］董红召，陈炜烽，郭明飞，等.基于车路一体化的车辆主动避撞系统关键技术的研究［J］.汽车工程，2010，32 (11):984-989.

DONG Hongzhao，CHEN Weifeng，GUO Mingfei，et al.A study on key technologies of vehicle active collision avoidance system based on VII technology［J］.Automotive Engineering，2010，32(11):984-989.

［3］徐友春，王荣本，李兵，等.世界智能车辆近况综述［J］.汽车工程，2011，23(5):289-295.

XU Youchun，WANG Rongben，LI Bing，et al.A Summary of Worldwide Intelligent Vehicle［J］.Automotive Engineering，2001，23(5):289-295.

［4］宋晓琳，冯广刚，杨济匡.汽车主动避撞系统的发展现状及趋势［J］.汽车工程，2008，30(4):285-290.

SONG Xiaolin，FENG Guanggang，YANG Jikuang.The current state and trends of automotive active collision avoidance system［J］.Automotive Engineering，2008，30(4): 285-290.

［5］侯德藻，李克强，郑四发，等.汽车主动避撞系统中的报警方法及其关键技术［J］.汽车工程，2002，24(5):438-444.

HOU Dezao，LI Keqiang，ZHENG Sifa，et al.The warning algorithm and some key technologies of vehicle collision avoidance system［J］.Automotive Engineering，2002，24 (5):438-441.

［6］ZHENG Bing，PAHNGROC O H，BANY L.Active steering control with front wheel steering［C］//Proceedings of the 2004 American Control Conference.Boston，USA，2004: 1475-1480.

［7］TILMAN B，DIRK O，BILIN A G，et al.Robust vehicle steering control design based on the disturbance observer［J］.Annual Reviews in Control，2002，26:139-149.

［8］韩京清.从PID技术到“自抗扰控制”技术［J］.控制工程，2002，9(3):13-18.

HAN Jingqing.From PID technique to active disturbances rejection control techique［J］.Control Engineering of China，2002，9(3):13-18.

［9］GAO Qiang，SUN zhan，YANG guolai，et al.A novel active disturbance rejection-based control strategy for a gun control system［J］.Journal of Mechanical Science and Technology，2012，26(12):4141-4148.

［10］韩京清.扩张状态观测器参与菲波纳奇数列［J］.控制工程，2008，15(S1):1-3.

HAN Jingqing.Parameters of the extended state observer and Fibonacci sequence［J］.Control Engineering of China，2008，15(S1):1-3.

［11］余志生，夏群生，赵六奇，等.汽车理论［M］.北京:机械工业出版社，2006:47-52.

［12］赵又群，汪伟，许健雄，等.避障工况下的汽车转向操纵动态特性分析［J］.哈尔滨工程大学学报，2013，34 (8):957-966.

ZHAO Youqun，WANG Wei，XU Jianxiong，et al.Analysis of dynamic characteristics of vehicle steering control for collision avoidance［J］.Journal of Harbin Engineering U-niversity，2013，34(8):957-966.

［13］SLEDGE N H，MARSHEK K M.Comparison of ideal vehicle lane-change trajectories［J］.Research into Vehicle Dynamics and Simulation，1997(10):233-256.

［14］SOUDBAKHSH D，ESKANDARIAN A.Comparison of linear and non-linear controllers for active steering of vehicles in evasive manoeuvres［J］.Proceedings of the Institution of Mechanical Engineers，part I:Journal of Systems and Control Engineering，2011，226:215-232.

［15］ISERMANN R，MANNALE R，SCHMITT K.Collision-avoidance systems proreta:situation analysis and intervention control［J］.Control Engineering Practice，2012，20 (11):1236-1246.