电场和温度对量子线中强耦合束缚极化子性质的影响

丁朝华, 鲍继平, 孙银凤, 王旭颖

(内蒙古民族大学物理与电子信息学院, 通辽 028043)

电场和温度对量子线中强耦合束缚极化子性质的影响

丁朝华, 鲍继平, 孙银凤, 王旭颖

(内蒙古民族大学物理与电子信息学院, 通辽 028043)

采用线性组合算符和幺正变换相结合方法研究了电场和温度对量子线中强耦合束缚极化子性质的影响.计算了在电场和温度影响下抛物量子线中强耦合束缚极化子的基态能量、平均声子数和振动频率.数值计算结果表明:束缚极化子的基态能量随约束强度、库仑束缚势和电场强度的增大而逐渐增大；平均声子数随温度、耦合强度的增大呈现递增关系, 随库仑束缚势的加大呈现递减关系；振动频率随耦合强度和温度的增大而增大, 随库仑束缚势的减小而增大.

电场； 量子线； 束缚极化子； 强耦合； 温度

1 引 言

以量子点、量子线和量子阱等为代表的低维量子系统具有很多有趣的量子现象和量子效应, 这些现象和效应被广泛地用来开发具有新原理和新结构的量子器件, 因此, 对低维量子系统性质的研究引起了国内外许多学者的广泛关注, 人们采用各种方法研究了低维量子系统中极化子的性质.Ghazi[1]等采用准一维有效势模型中的有限差分法和有效质量近似, 研究了氮化铟镓/氮化镓抛物线QWW结合能的斯塔克效应；Safarpour[2]等利用变分法研究了在一个放置在类氢杂质圆柱形纳米线中心的球形量子点的结合能及其光学性质；Yeranosyan[3]等用Landau-Pekar变分法研究了电场和磁场作用下杂质态圆柱形纳米线的声子限域效应；Xiao[4,5]和Li[6,7]等用Pekar变分法研究了电场影响下量子棒和量子点中强耦合和弱耦合极化子基态和激发态的性质；Chen等[8]采用Landau-Pekar变分法研究了二维和三维量子点中束缚极化子的有效质量；本文作者曾使用线性组合算符和幺正变换相结合的方法研究了量子线中和量子棒中极化子基态和激发态的性质[10,11].但到目前为止, 采用线性组合算符和幺正变换相结合方法研究电场和温度对量子线中束缚极化子性质的影响者甚少.本文将采用线性组合算符和幺正变换相结合方法研究电场和温度对抛物量子线中强耦合束缚极化子性质的影响.

2 理论计算

极性半导体材料形成的量子线中, 电子被束缚于氢化杂质中并与极性半导体的体纵光学声子场相互作用, 取线长方向为z方向, 该量子线受到沿着z方向的均匀外电场F(0,0,F)的作用, 设量子线的束缚势为抛物势, 考虑到电子与体纵光学声子(LO声子)之间的相互作用, 在有效质量近似下, 该系统的哈密顿量为

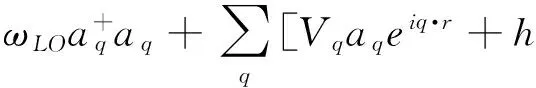
(1)

其中

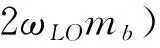
=(2mbωLO/ħ)1/2(e2/2ħωLO)(1/ε∞-1/ε0)

(2)

以上诸式V和mb分别代表晶体的体积和电子的带质量,ε0为静介电常数,ε∞为高频介电常数,α和ω0分别表示LO声子之间的耦合强度和量子线的约束强度.

(3)

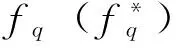
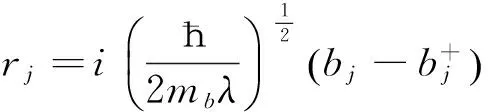
(4)

其中,j=x,y,z,λ为变分参量, 它表示电子的振动频率.则哈密顿量变为

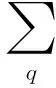
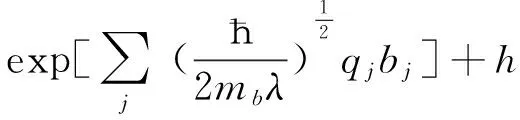
(5)

选取系统的尝试波函数为

|ψ〉=|φ(ρ)〉|nq〉|nj〉

(6)

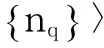
(5)式对尝试波函数的期待值为

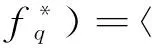
(7)

式(7)通过对fq变分, 经过计算可得

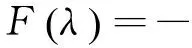
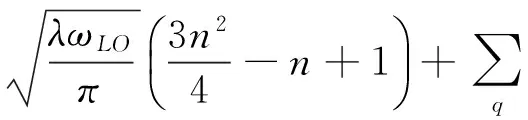
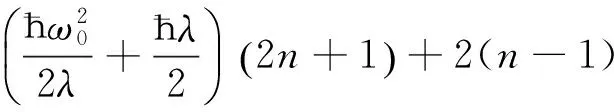
(8)

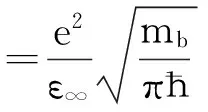
最后再将 (8) 式对λ变分, 可以获得极化子的振动频率λ满足的方程为

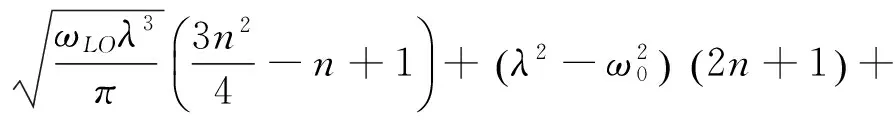
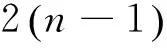
(9)

通过求解(9)式的方程, 可解得极化子的振动频率为λ=λ0, 再将该值代入(9)式, 可以获得在电场影响下抛物量子线中强耦合束缚极化子的基态能量为

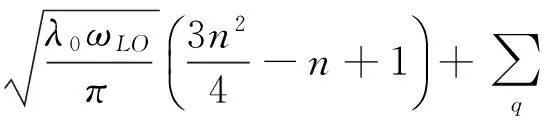
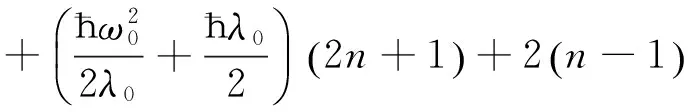
(10)

在外加电场作用下, 抛物量子线中强耦合束缚极化子的平均声子数为

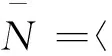
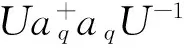
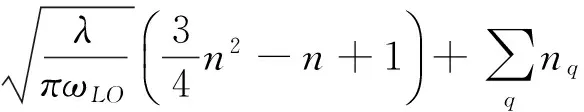
(11)

在一定温度下, 电子与声子体系不再全部处于最低能态, 晶体不但激发实声子, 同时也使抛物势中的电子受到激发. 此时, 极化子的性质是对电子与声子体系所有态的的统计平均.根据量子统计力学的知识可知, 系统的极化子数和声子数的平均值分别为

(12)

(12)式中kB是玻尔兹曼常数.

将(10)式和(11)式的声子数和极化子数分别用(12)式的平均值代替, 就可以得到在电场和温度影响下抛物量子线中强耦合束缚极化子的基态能量、平均声子数和振动频率表达式分别为

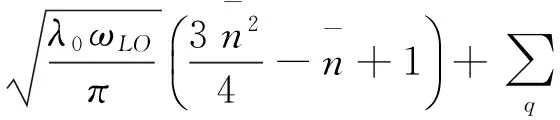
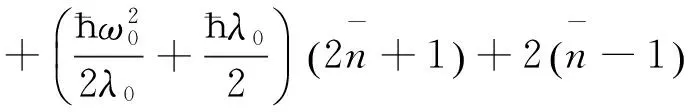
(13)

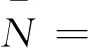
(14)

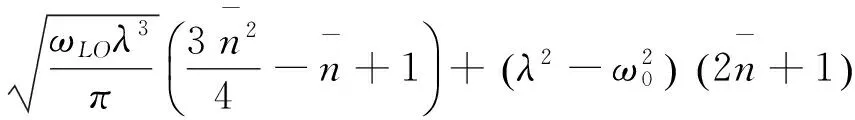
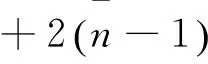
(15)

3 数值结果与讨论

为了能够更加明确体现在电场和温度作用下抛物量子线中强耦合束缚极化子的基态能量、平均声子数和振动频率随库仑束缚势、约束强度、耦合强度、温度以及电场强度变化关系, 选取极化子单位进行数值分析, 具体结果示于图1—图6中.图中所有能量的单位均为ħωLO, 而振动频率λ的单位则是ωLO.

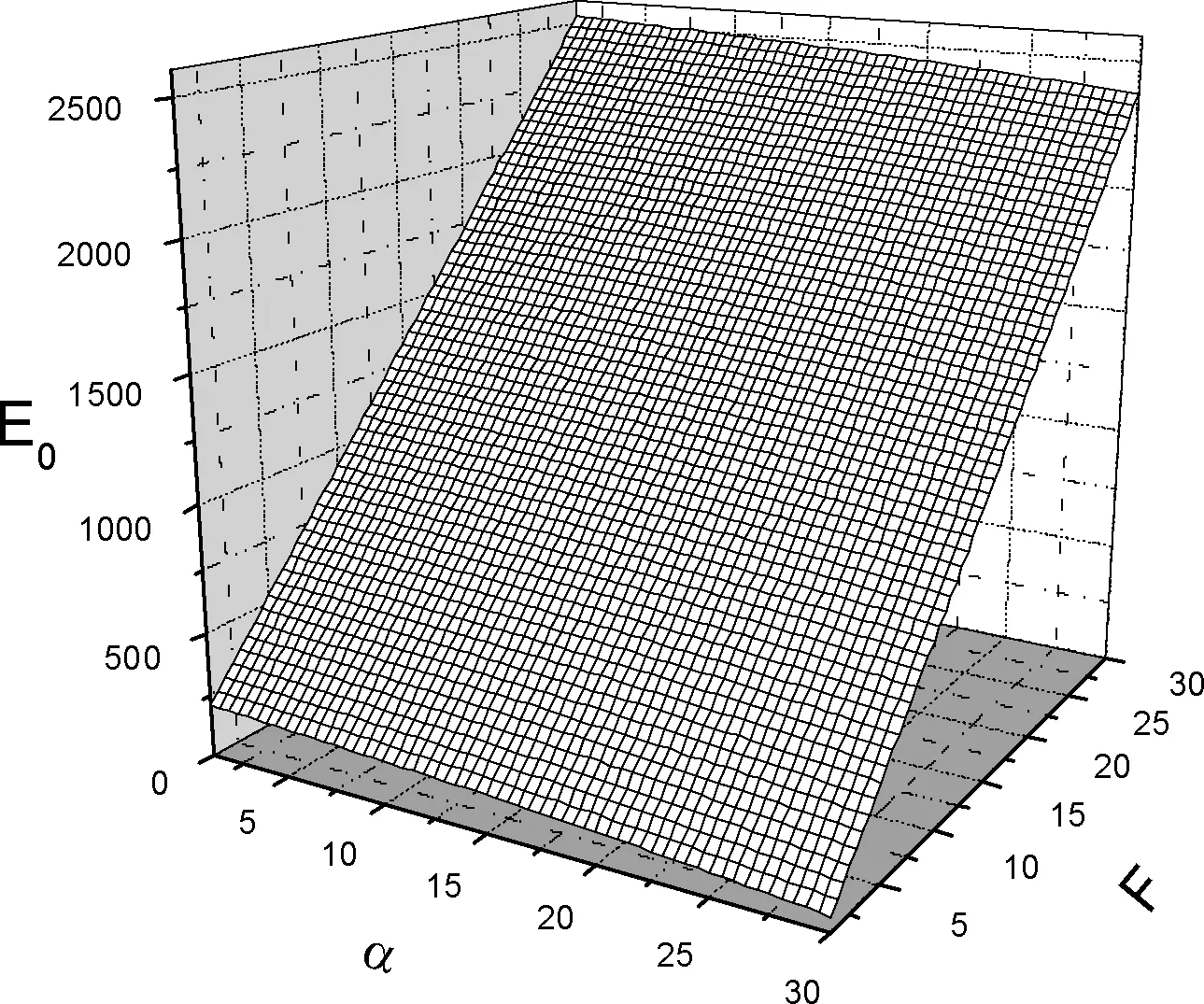
图1 极化子的基态能量与耦合强度、电场强度的关系Fig.1 Relational curve of the ground state energy and the coupling strength and the electric-field strength of polaron

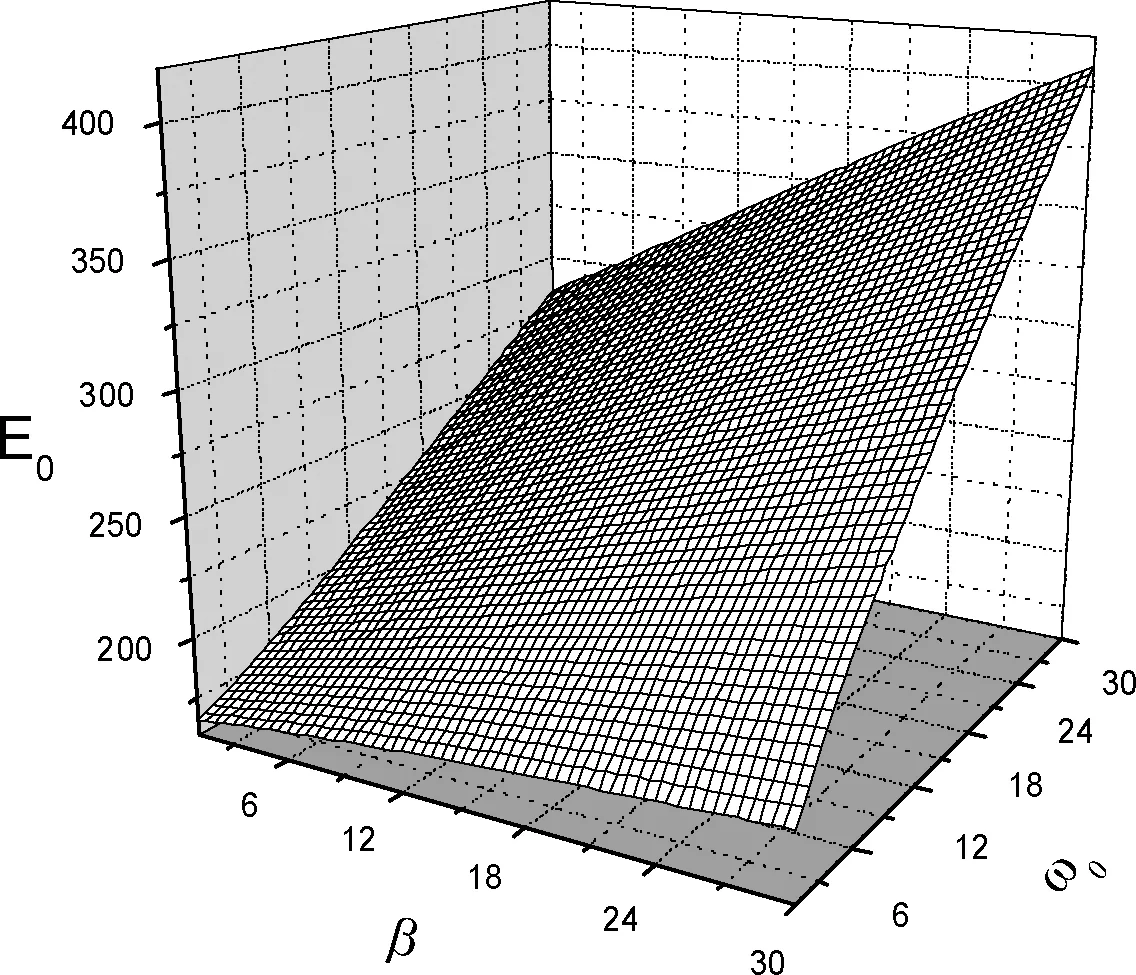
图2 极化子的基态能量与库仑束缚势和约束强度的关系Fig.2 Relational curves of the ground state energy and the coulomb bound potential and the constraint strength of polaron

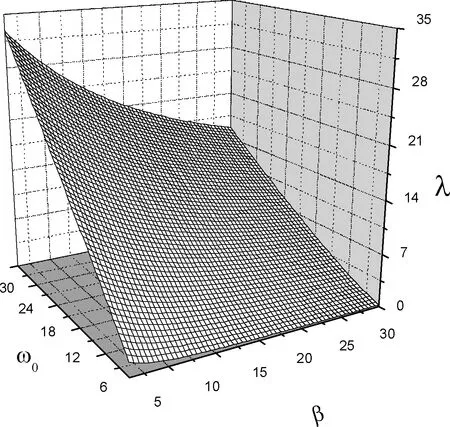
图3 振动频率与库仑束缚势、约束强度的关系Fig.3 The correlation among the vibration frequency, the coulomb bound potential and the constraint strength of polaron

图1为基态能量E0与耦合强度α和电场强度F之间的关系曲线.由曲线可知, 基态能量会随着耦合强度的增强而减弱, 同时随着外加电场的变强而加强.图2给出了基态能量E0和库仑束缚势β及约束强度ω0的函数关系.从图2的曲线可以看出, 基态能量随库仑束缚势的加强而变大, 同时也伴随着约束强度的增强而增加.图3反映了振动频率λ和库仑束缚势β以及约束强度ω0之间的函数关系.从图3可知振动频率随库仑束缚势的增强而变慢, 同时随约束强度的增大而加快.

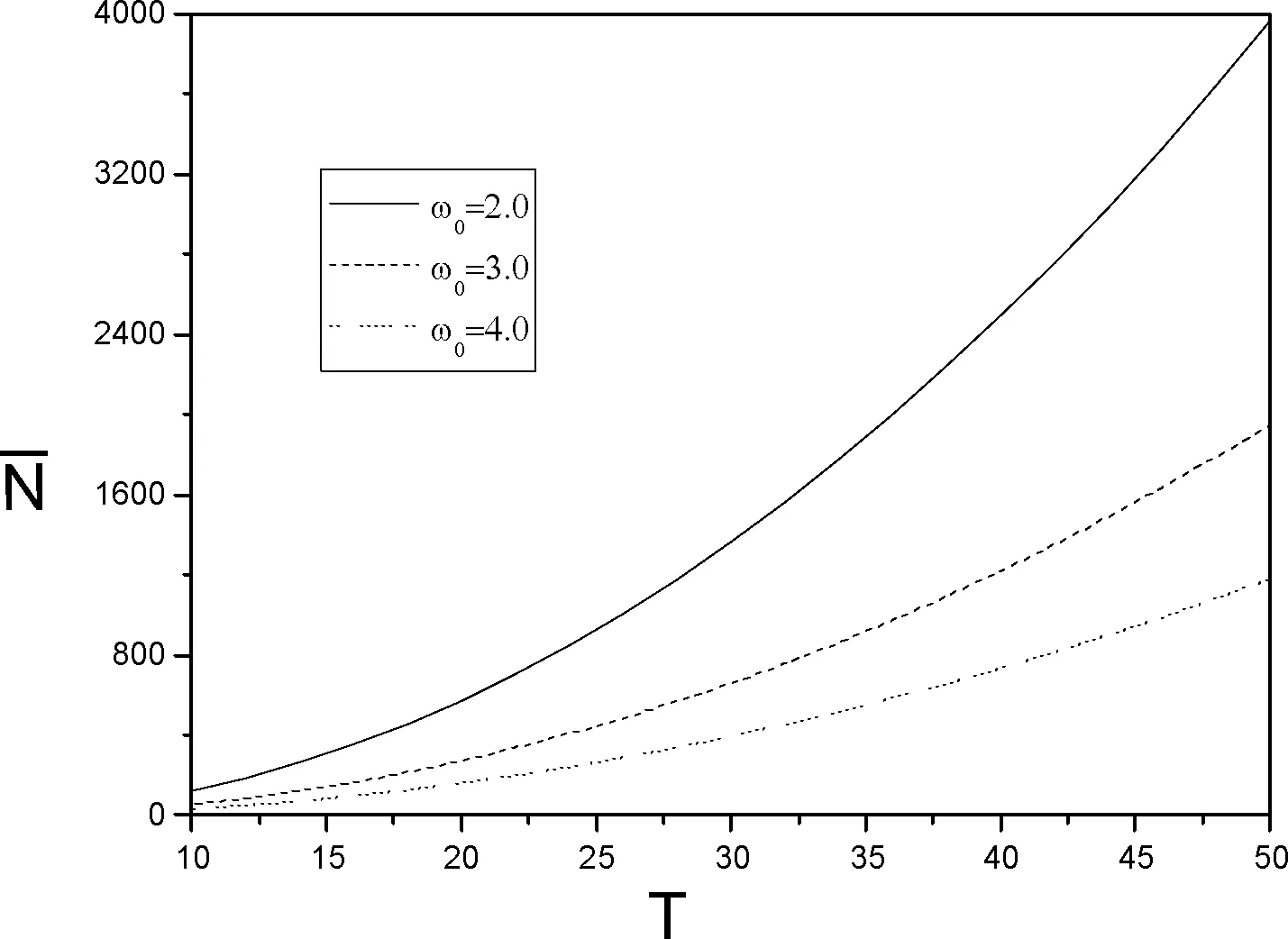
图4 极化子的平均声子数与温度的关系Fig.4 Relational curve of the mean number of phonon and the temperature of polaron

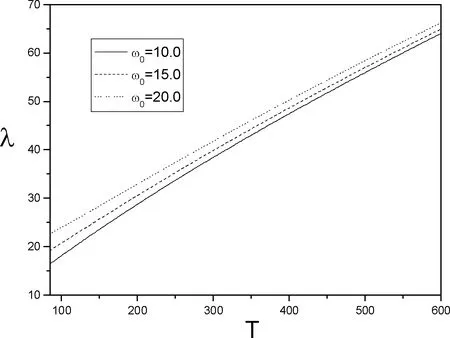
图5 极化子的振动频率与温度的关系曲线Fig.5 The correlation between the vibration frequency and the temperature

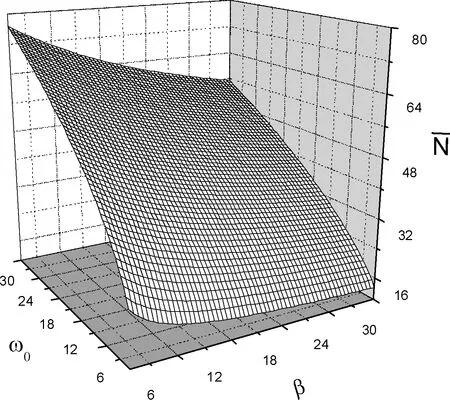
图6 平均声子数与库仑束缚势、约束强度的关系Fig.6 Relational of the mean number, the Coulomb bound potential and the constraint strength of polaron

4 结 论

本文采用线性组合算符和幺正变换相结合方法, 研究了电场和温度对量子线中强耦合束缚极化子性质的影响.计算了在电场和温度影响下抛物量子线中强耦合束缚极化子的基态能量、平均声子数和振动频率.研究结果表明, 在外加电场和温度共同作用下的抛物量子线中强耦合束缚极化子基态能量随着约束强度、库仑束缚势和外加电场强度的增大而变强；平均声子数随约束强度、耦合强度和温度的加强而增多, 同时随库仑束缚势的加强而大大减少；振动频率随约束强度、耦合强度和温度的增大而变快, 同时还会随着库仑束缚势的增大而变慢.

[1]GhaziH,ZorkaniI,JorioA.Starkeffect-dependentofground-statedonorbindingenergyinInGaN/GaNparabolicQWW[J]. Phys.B, 2013, 412: 87.

[2]SafarpourG,BaratiM,ZamaniA, et al.Bindingenergyandopticalpropertiesofanoff-centerhydrogenicdonorimpurityinasphericalquantumdotplacedatthecenterofacylindricalnano-wire[J]. Journal of Luminescence, 2014, 145: 990.

[3]YeranosyanMA,ShahbandariAG,VartanianAL.Thephononconfinementeffectontheimpuritystatesincylindricalnanowirewithafiniteconfiningpotentialinpresenceofelectricandmagneticfields[J]. Advanced Materials Research, 2014, 829: 795.

[4]XiaoJL,ZhaoCL.Propertiesofstrong-couplingmagnetopolaroninquantumrods[J]. Superlatt. Microstruc., 2011, 49(1): 9.

[5]XiaoJL.InfluencesoftemperatureandCoulombboundpotentialonthepropertiesofquantumrodqubit[J]. Superlatt. Microstruc., 2013, 60(1): 248.

[6]LiWP,YinJW,YuYF, et al.Theinfluenceofelectricfieldontheground-statelifetimeofpolaroninaparabolicquantumdot[J].Mod. Phys. Lett.B, 2011, 25(3): 203.

[7]LiZX,YinCH.Theground-statetransitionprobabilityofimpurityboundpolaroninquantumrod[J]. Phys.B, 2013, 418(1): 69.

[8]ChenSH.Theeffectivemassofimpurity-boundpolaroninatwo-andthree-dimensionalquantumdot[J]. J. Low. Temp. Phys., 2013, 170: 108.

[9]DingZH,XiaoJL.Vibrationalfrequencyofastrong-couplingpolaroninquantumrodsatafinitetemperatures[J]. Chin. Phys.B, 2011, 20(9): 0907104-1.

[10]DingZH,SunY,XiaoJL.Opticalphononeffectinanasymmetricquantumdotqubit[J]. International Journal of Quantum Information, 2012, 10(7): 1250077-1.

[11]HeR,DingZH,BaoJP.Propertiesofexcitedstateofboundpolaroninquantumwires[J]. J. At. Mol. Phys., 2011, 28(5): 949(inChinese)[何锐, 丁朝华, 鲍继平.量子线中强耦合束缚极化子激发态的性质[J].原子与分子物理学报, 2011, 28(5): 949]

Influences of electric field and temperature on the properties of strong-coupling bound polaron in quantum wires

DING Zhao-Hua, BAO Ji-Ping, SUN Yin-Feng, WANG Xu-Ying

(College of Physics and Electronic Information, Inner Mongolia University for Nationalites, Tongliao 028043, China)

The influences of electric field and temperature on properties of strong-coupling bound polaron in parabolic quantum wires are studied by using of the linear combination operator and the unitary transformation methods. The ground state energy, the mean number of phonon and the vibrational frequency were calculated. The numerical results show that the ground state energy increases with the increasing Coulomb bound potential and electric field. The mean number of phonon is a increasing function of the temperature and the confinement strength, and it is a decreasing function of the Coulomb bound potential. The variation frequency increases with the increasing of electron-phonon coupling strength and temperature. However, it decreases with increasing the Coulomb bound potential.

Quantum wire; Electric field; Bound polaron; Strong-coupling; Temperature

2014-04-19

国家自然科学基金(11304143)；内蒙古自治区高校科研项目(NJZY14189)

丁朝华(1962—)，女，内蒙古通辽人，教授，主要从事凝聚态光学性质的研究.E-mail:dzhaohua@126.com

103969/j.issn.1000-0364.2015.10.019

O469

A

1000-0364(2015)05-0836-05