飞秒脉冲激光在V型有机分子介质中的动力学表征

刘瑞金, 孙玉萍

(山东理工大学理学院, 淄博 255049)

飞秒脉冲激光在V型有机分子介质中的动力学表征

刘瑞金, 孙玉萍

(山东理工大学理学院, 淄博 255049)

在不采用旋波近似和慢变幅近似的条件下, 通过采用时域有限差分法和预估矫正法数值求解Maxwell-Bloch方程, 模拟了飞秒激光脉冲在V型三能级有机分子介质中的传播过程, 研究了介质密度对单色脉冲共振传播的影响以及两色飞秒脉冲在该分子体系中的传播情况.有机分子的电子结构和电偶极矩是在密度泛函理论水平上利用从头计算方法得到的.研究结果表明, 介质密度对脉冲演化产生较大的影响, 随介质密度的增大, 非线性效应增强, 面积定理逐渐失效；两色脉冲的相对强度及初始相位对各能级的粒子数分布有很大的影响.

非线性光学； Maxwell-Bloch方程； 飞秒脉冲； 面积定理； 两色脉冲

1 引 言

光与物质相互作用的内部机制, 一直是人们关注的热点课题.尤其是近年来基于各种科学技术的提高, 超短超强激光、同步辐射光源以及X射线自由电子激光的发展[1,2], 使人类对光与物质相互作用的探索进入了一个全新的阶段, 对研究光物理、光化学、光生物学、激光光谱、表面物理、非线性光学、天体物理等学科中的超快过程具有较高的应用价值[3].通过研究超短脉冲与有机分子的相互作用, 一方面可以获取有机介质的有关光电性质, 揭示有机分子材料结构与性质之间的关系；另一方面通过研究脉冲的演化情况, 为进一步设计激光脉冲提供理论指导.

基于光与物质相互作用的半经典理论, 在研究过程中把激光场看作是经典电磁场, 用麦克斯韦方程组来描述, 把介质看作是量子系统, 用密度矩阵方程来描述.在实际的理论研究过程中人们往往对实际复杂的介质体系采用少态模型进行简化, 即根据各能级与光场的耦合情况把实际参与相互作用的重要能级提取出来.基于二能级模型, 人们通过对光与物质的相互作用研究发现了一系列有趣的现象, 包括自感应透明[4]、拉比振荡[5]、面积定理[6]、光子回波[7]等；基于级联三能级模型, 研究了四波混频、双光子吸收光限幅效应[8,9]等等.然而, 对于飞秒脉冲在V型三能级有机分子中的传播特性研究至今未见报道.

本文所研究的分子属一维对称π共轭分子体系, 这类有机分子最大的单光子和双光子吸收截面对应体系的不同激发态[10, 11], 探索该分子介质与超短脉冲相互作用, 应采用V型三能级模型进行简化.本文研究了介质密度对脉冲演化的影响以及两色脉冲在该体系中的传播特性, 主要讨论了电场的时空演化和该分子体系各能级粒子数占有率的变化情况.

2 理论方法

当超强超短脉冲激光与介质相互作用时, 经常伴随有受激拉曼散射、自发辐射放大等非线性过程发生[12-14].为了精确描述这一过程, 在不采用旋波近似和慢变幅近似的条件下, 我们通过采用时域有限差分法和预估矫正法数值求解Maxwell-Bloch方程.

引入唯象衰减项后的密度矩阵方程为

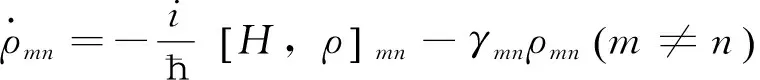
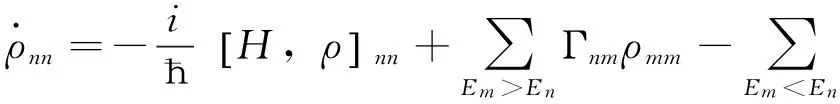
(1)

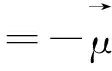
设光场沿z方向入射, 电场只有x分量, 磁场只有y分量, 分子介质电导率σ=0, 相对磁导率μr=1, 则在分子中传播的超短脉冲激光所满足的麦克斯韦方程为

,

(2)

根据密度矩阵理论, 三能级体系的宏观极化强度可表示为

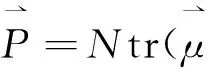
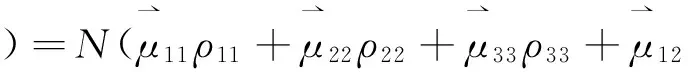
(3)

式中N为分子数密度.

3 结果与讨论

本文所研究分子的结构如图1所示.

图1 分子的结构示意图Fig.1 The structure diagram of molecule

利用密度泛函理论, 量化计算结果表明, 在低能量范围内该分子有两个电荷转移态(第一激发态和第四激发态), 基态分别与两个电荷转移态间有较大的跃迁偶极矩, μ01=4.8363×10-29Cm和μ04=2.3840×10-29Cm, 而其它态之间的跃迁偶极矩约为零.由于该分子的对称性, 分子各能级的固有偶极矩约为零.两个激发态的能量分别为E1=2.70eV和E4=3.67eV.因此, 在研究超短脉冲与该分子体系相互作用时, 在低能量范围内可以将该分子简化为V型三能级体系, 如图2所示, 其中1为基态, 2为第一激发态, 3为第4激发态.

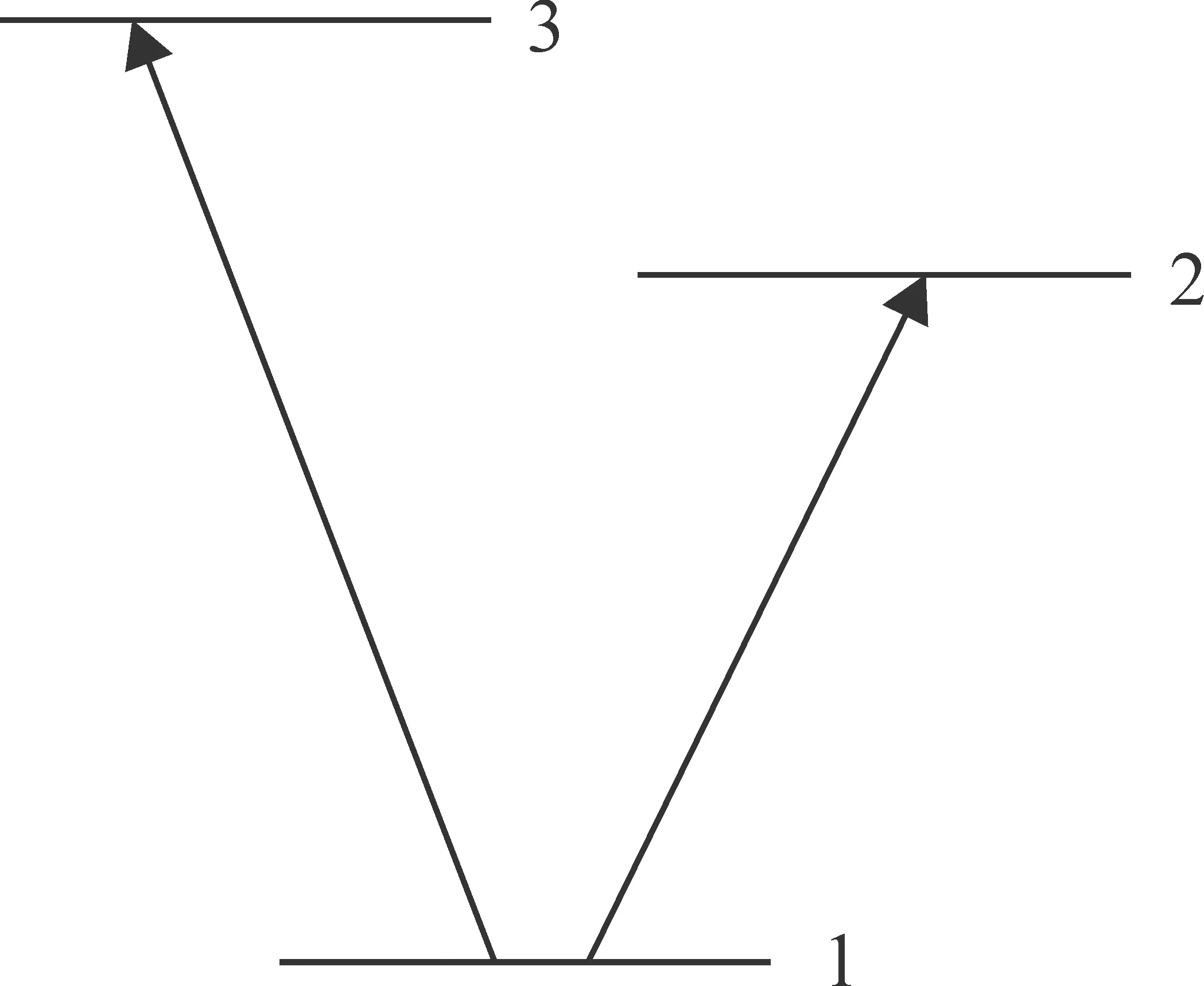
图2 能级结构Fig.2 Energy-level scheme

设初始时刻体系处于基态, ρ11(t=0)=1, 各态之间是非相干的, ρmn(t=0)=0(m≠n), 各密度矩阵元的衰减速率取值为:γmn=1.0×1013/s(m≠n),Γ21=Γ31=1.0×109/s,Γ32=0.选择的入射脉冲波形为双曲正割型Ex(z,t=0)=F0sech[(z+z0)/ct0]×cos[ωp(z+z0)/c], 其中F0是最大峰值, 脉冲宽度τp=1.76t0, z0的选取要保证在初始时刻脉冲进入介质很少.分别选取入射脉冲的频率等于能级1和2、1和3之间的共振频率.对双曲正割型脉冲, 脉冲面积可表示为A=μF0t0π/ħ.

首先我们研究了在满足单光子共振条件ω=ω12下, 粒子数密度对脉冲在该分子体系中传播过程的影响；然后讨论了当ωp1=ω12, ωp2=ω13时两色超短脉冲激光与V型三能级体系的相互作用过程及两脉冲的初始相位对该过程的影响.

3.1 在满足单光子共振条件ω=ω12下, 脉冲在该分子体系中的传播过程

保持脉冲宽度τp=5fs不变时, 面积为1.4π的脉冲电场及各能级粒子数占有率随传播距离的演化情况如图1和图2所示, 对应粒子数密度分别取7.0×1024/m3、7.0×1025/m3.

图1(a)给出了对应的电场载波(点线)及采用慢变幅近似和旋波近似时电场包络(实线)的时间演化情况, 可以看出, 当n=7.0×1024/m3时, 1.4π面积脉冲在传播过程中逐渐发生分裂, 主脉冲强度略有减小且产生了许多幅度较小的子脉冲；对于该脉冲, 采用SVEA和RWA可以给出很好的描述, 且在演化过程中出现了负面积.图1(b)给出了各能级粒子数占有率的演化情况.由图可见, 电场由刚开始能使粒子数反转发生大约0.7个拉比振荡演化到能使其发生一个完整的拉比振荡, 说明1.4π面积脉冲通过脉冲分裂逐渐演化为2π脉冲, 基本上满足面积定理；由于所加电场强度较弱, 能级3上的粒子数变化非常小, 表明能级3与光场的耦合作用很弱.

当粒子数密度n取7.0×1025/m3时, 脉冲的演化情况如图2所示.可以看出, 此时SVEA和RWA失效, 不能对脉冲演化给出较好的描述, 1.4π面积脉冲在传播过程中同样发生了分裂, 在主脉冲后面出现了多个电场幅度较小的脉冲.从粒子数占有率的变化可知, 各能级的粒子数发生了多次较弱的振荡, 1.4π面积脉冲并没有演化为2π脉冲, 而是演化为零面积脉冲, 逐渐被介质所吸收, 面积定理失效.随着传播距离的增加, 脉冲强度明显减弱, 不足以使基态的粒子全部激发到高能级, 当脉冲传播到1.4μm处时, 基态粒子约有53%被激发到高能级, 当脉冲传播到7μm处时仅有30%的粒子被激发到高能级.

比较以上两种情况, 很显然介质密度对脉冲传播过程产生较大的影响.图3给出了粒子数密度分别取不同数值时, 6π面积脉冲对应电场的演化情况.同样可以看出, 只有粒子数密度较小时面积定理及慢变幅近似和旋波近似才有效；粒子数密度越高, 介质所表现出的非线性光学性质越明显, 脉冲在传播过程中越容易发生分裂, 分裂后的多个子脉冲强度较弱, 逐渐被介质所吸收, 面积定理随之失效, 不能再准确地描述脉冲的演化过程.

3.2 当ωp1=ω12, ωp2=ω13时, 两色脉冲在该分子介质中的传播

对于V型三能级体系, 两色脉冲演化面积定理公式:

(4)

其中θa和θb分别表示两入射脉冲的面积, 其中α是介质的吸收系数[15], 当θa=0或θb=0时即二能级面积定理公式.

取两入射脉冲的频率满足ωp1=ω12, ωp2=ω13单光子共振条件, 初始时刻两光场相互重叠, 无位相差, 粒子全部处于基态.我们研究了(mπ,nπ)的两色脉冲在m、n取不同数值时的演化情况, 如图6所示(z=14μm).

由电场随时间的演化过程可以看出, 在传播过程中两脉冲出现分裂现象, 即超短脉冲在介质中通过脉冲分裂来进行面积演化, 而不像长脉冲那样通过脉冲压缩或展宽.因为超短脉冲的脉宽较窄, 当介质发生受激辐射时, 主脉冲已过去, 介质辐射出的能量就留在了主脉冲后面, 从而导致脉冲发生分裂[16].由粒子数占有率的分布图可以看出, 在V型体系中能级2和3与光场的耦合作用都较强；在脉冲前沿, 处于基态的粒子被激发到能级3上, 而能级2上的粒子数在很短的时间内仍为零, 两激发态之间不存在电偶极跃迁, 能级2和3上的粒子数均来自基态粒子的受激激发. 图中各能级粒子数占有率在电场的零值处表现出的振荡特性主要是由于电场时间导数项作用引起的[17].

从基态粒子数的振荡情况看, 面积为1.3π的两脉冲(图a-2)和面积为2π的两脉冲(图b-2)逐渐演化为2π脉冲, 基态的粒子数发生一次近完整的振荡；而面积为2.5π的两脉冲(图c-2)逐渐演化为4π脉冲, 基态的粒子数发生两次近完整的振荡, 同样一个3.2π脉冲和一个1.6π脉冲演化成4π脉冲(如图d-2所示), 这说明面积定理可以用来较好地描述两色脉冲在V型三能级体系中的传播情况.

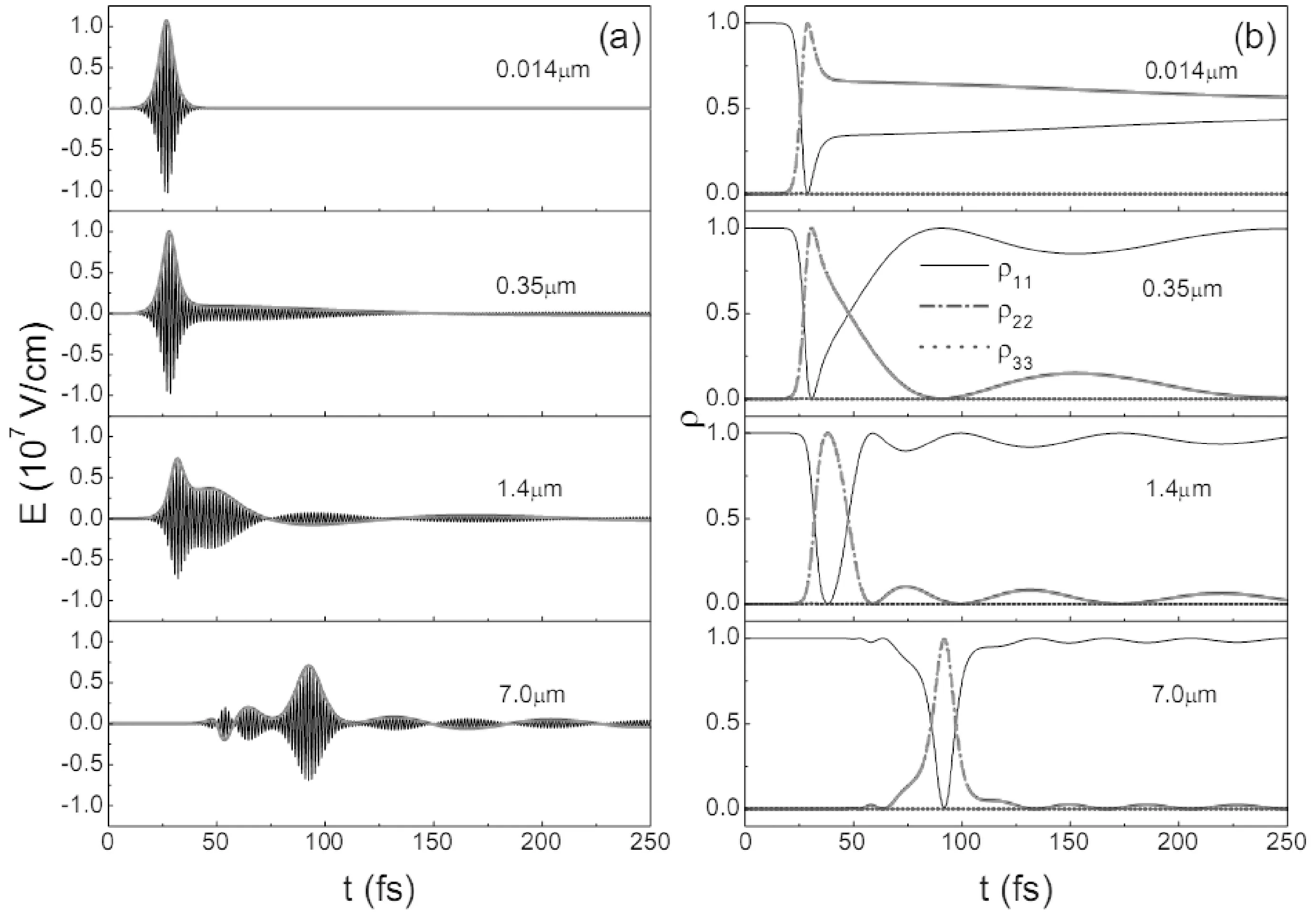
图3 ω=ω12时, 1.4π脉冲在不同传播距离处的电场(a)及各能级粒子数占有率(b)的时间演化(n=7.0×1024/m3)Fig.3 The temporal shapes of the pulse (a) and the populations of different states (b) for the different propagation distances with ω=ω12, θ=1.4π and n=7.0×1024/m3

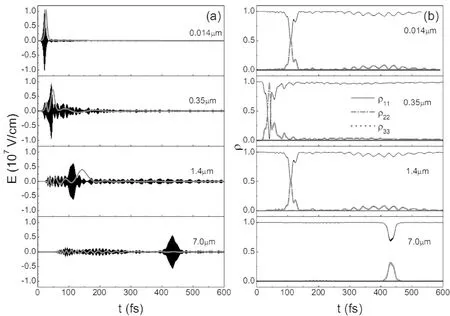
图4 ω=ω12时, 1.4π脉冲在不同传播距离处的电场(a)及各能级粒子数占有率(b)的时间演化(n=7.0×1025/m3)Fig.4 The temporal shapes of the pulse (a) and the populations of different states (b) for different propagation distances with ω=ω12, θ=1.4π and n=7.0×1025/m3

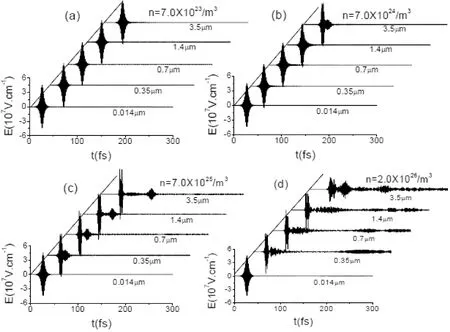
图5 粒子数密度取不同数值时, 面积为6π的脉冲电场随时间的演化过程Fig.5 The evolution of electric fields as propagation distances with different concentrations for θ=6π

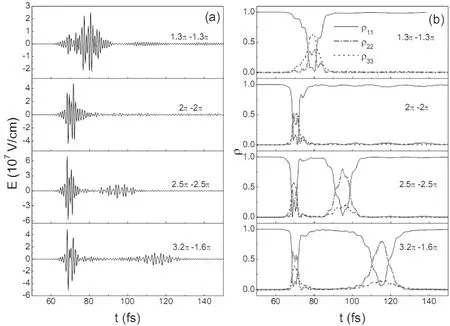
图6 ωp1=ω12, ωp2=ω13时, 不同面积的两色脉冲传播到14um处的电场(a)及各能级粒子数占有率(b)随时间的演化情况Fig.6 The temporal shapes of electric fields (a) and the populations of different states (b) at 14um for two-color pulses with different areas with ωp1=ω12, ωp2=ω13

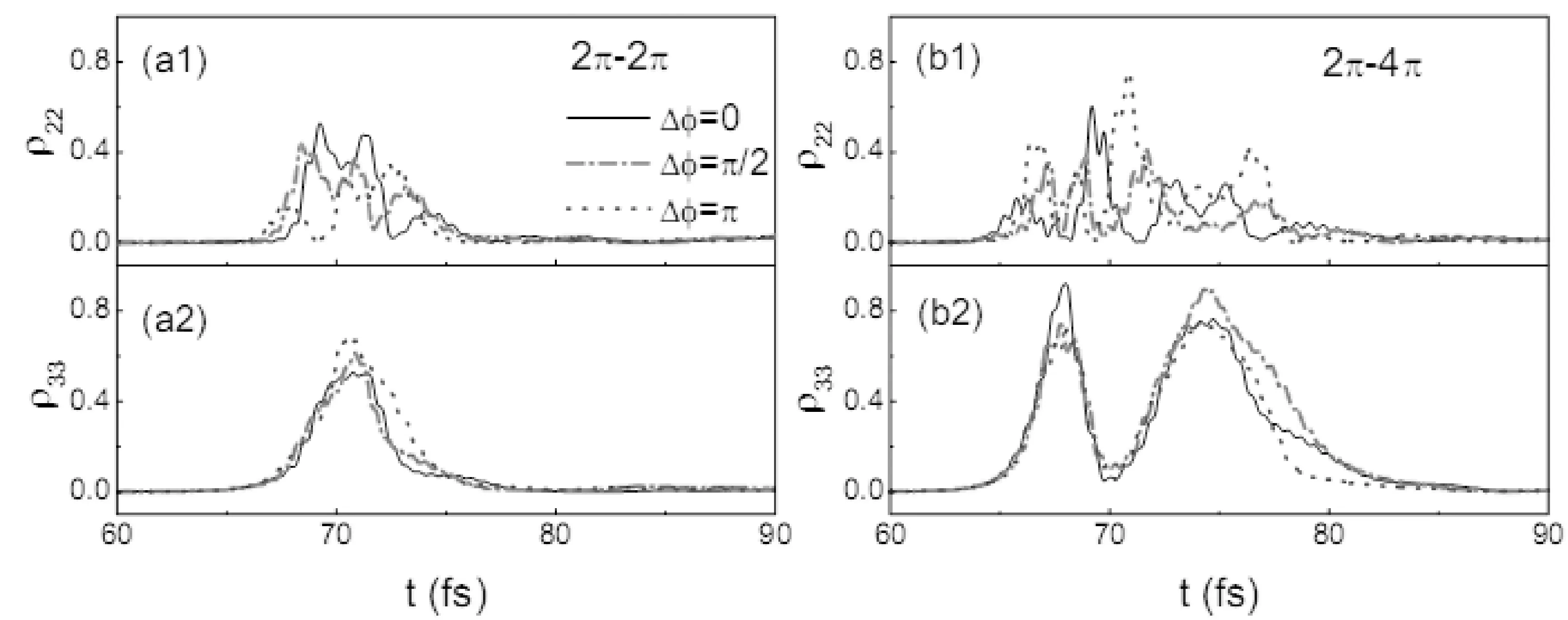
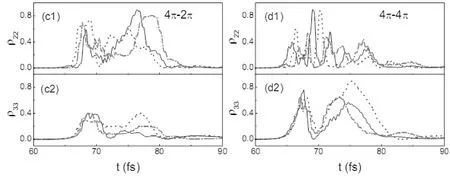
图7 两脉冲的初相位取不同值时, 各能级的粒子数占有率随时间的变化情况Fig.7 The evolution of the populations of excited stateswith time for the two-color laser pulses with different relative phases

3.3 两色脉冲的初始相位差对脉冲演化的影响

当两色脉冲的初始相位差取不同数值时, 我们研究了(mπ,nπ)两色脉冲的传播, 图5给出了m、n取不同数值时两激发态的粒子数占有率随时间的演化情况.

由图可以明显看出两脉冲的初始相位差对各能级的粒子数占有率分布有很大的影响, 各能级粒子数分布的峰值大小和峰值出现的时间与脉冲的相对强度有关[18], 同时受两脉冲间初始位相差的影响, 因此设计脉冲时可以通过控制两脉冲的初始相位来调节各能级的粒子数分布.

4 结 论

以半经典电磁场理论为基础, 采用时域有限差分法和预估矫正法数值求解麦克斯韦—布洛赫方程, 对超短脉冲与V型三能级体系的相互作用进行了研究.研究结果表明, 单色脉冲共振传播时介质密度对脉冲演化有很大的影响, 随介质密度增大, 非线性效应增强, 面积定理逐渐失效；对于两色脉冲在该体系中的传播, 两脉冲的相对强度以及初始相位差对粒子数分布影响较大, 面积定理可以用来较好地描述两色脉冲在V型三能级体系中的传播情况.

[1]http://www.xfel.eu/overview/flash/.

[2]https://portal.slac.stanford.edu/sites/lcls_public/Pages/Default.aspx.

[3]CheHS,ShaoY.Laserchaoticsecurecommunications[J]. Laser & Optoelectronics Progress, 2003, 40(5): 7(inChinese) [车会生, 邵毅. 激光混沌保密通信[J]. 激光与光电子学进展, 2003, 40(5): 7]

[4]McCallSL,HahnEL.Self-inducedtransparency[J]. Phys. Rev., 1969, 183(2): 457.

[5]McCallSL,HahnEL.Self-inducedtransparencybypulsedcoherentlight[J]. Phys. Rev. Lett., 1967, 18(21): 908.

[6]AllenL,EberlyJH. Optical Resonance and Two-Level Atoms[M].NewYork:Wiley, 1975.

[7]AbellaID,KurnitNA,HartmannSR.Photonechoes[J]. Phys. Rev., 1966, 141(1): 391.

[8]SunYP,LiuJC,WangCK.Effectoftime-dependentionizationonpropertiesoftheultrashortpulsepropagationandopticalpowerlimitinginatwo-photonabsorptionmolecularmedium[J]. Acta Physica Sinica, 2009, 58(6): 3934 (inChinese) [孙玉萍, 刘纪彩, 王传奎. 含时电离对飞秒脉冲激光在强双光子吸收介质中传播特性和光限幅行为的影响[J]. 物理学报, 2009, 58(6): 3934]

[9]SunYP,LiuJC,WangCK.Effectoftime-dependentionizationondynamicaltwo-photonabsorptioncrosssectionsofmolecularmedia[J]. Acta Optica Sinica, 2009, 29(6): 1621 (inChinese) [孙玉萍, 刘纪彩, 王传奎. 含时电离对分子动态双光子吸收截面的影响[J]. 光学学报, 2009, 29(6): 1621]

[10]WangCK,MacakP,LuoY, et al.Effectsofπcentersandsymmetryontwo-photonabsorptioncrosssectionsoforganicchromophores[J]. J. Chem. Phys., 2001, 114(22): 9813.

[11]SuY,WangCK,WangYH, et al.Theinfluenceofsymmetriesofthesubstituteddonorandacceptorontwo-photonabsorptioncrosssectionsoftrans-stilbenederivatives[J]. Acta Phys. Sin., 2004, 53(7): 2112 (inChinese) [苏燕, 王传奎, 王彦华, 等. 二苯乙烯衍生物分子双光子吸收截面:官能团对称性的影响[J]. 物理学报, 2004, 53(7): 2112]

[12]SunYP,LiuJC,WangCK, et al.Propagationofastrongx-raypulse:Pulsecompression,stimulatedRamanscattering,amplifiedspontaneousemission,lasingwithoutinversionandfour-wavemixing[J]. Phys. Rev.A, 2010, 81(1): 013812.

[13]SunYP,LiuJC,Gel’mukhanovF.Propagationofastrongx-raypulsefollowedbypulsecompression,amplifiedspontaneousemissionandlasingwithoutinversion[J]. J. Phys.B: At. Mol. Opt. Phys., 2009, 42(20): 201001.

[14]SunYP,LiuJC,Gel’mukhanovF.Slowdownandcompressionofstrongx-rayfree-electronpulsepropagatingthroughtheMgvapors[J]. Europhys. Lett., 2009, 87: 64002.

[15]RahmanA.OpticalpulsepropagationinV-typemedia[J]. Phys. Rev.A, 1999, 60(5): 4187.

[16]XiaoJ,WangZY,XuZZ.Areaevolutionofafew-cyclepulselaserinatwo-level-atommedium[J]. Phys. Rev.A, 2002, 65(3): 031402.

[17]SongXH,GongSQ,JinSQ, et al.Formationofhigherspectralcomponentsinatwo-levelmediumdrivenbytwo-colorultrashortlaserpulses[J]. Phys. Rev.A, 2004, 69(1): 015801.

[18]LoikoY,SerratC.Coherentandphase-sensitivephenomenaofultrashortlaserpulsespropagatinginthree-level∧-typesystemsstudiedwiththefinite-differencetime-domainmethod[J]. Phys. Rev.A, 2006, 73(6): 063809.

Dynamic characterization of femtosecond laser pulse in the V-type organic molecular media

LIU Rui-Jin, SUN Yu-Ping

(School of Science, Shandong University of Technology, Zibo 255049, China)

We simulate the propagation of the femtosecond laser pulses through the V-type three-level organic molecular medium by numerically resolving Maxwell-Bloch equations using finite-difference time-domain and iterative predictor-corrector technique beyond rotating-wave approximation and slowly varying envelope approximation. The effect of the molecular density on the pulse resonant propagation and the dynamics of two-color femtosecond pulses are studied. The electronic structure and dipole moments of the organic molecule are computed using the ab initio method at the level of density functional theory. The results show that the concentration of the sample has an obvious effect on the evolution of the pulse. Larger concentration results in stronger nonlinear effect, and area theorem becomes invalid as the value of molecular density increases; The relative intensity and the initial phase of two-color pulses have great impact on the population of the levels.

Nonlinear optics; Maxwell-Bloch equations; Femtosecond pulses; Area theorem; Two-color pulse

2014-04-13

国家自然科学基金(11204163);山东省优秀中青年科学家科研奖励基金(BS2013SF018)

刘瑞金(1963—)，男，副教授，硕士，主要从事强场激光动力学研究.

孙玉萍.E-mail:sunyuping821008@163.com

103969/j.issn.1000-0364.2015.10.018

O437.1

A

1000-0364(2015)05-0829-07