利用WBEPM模型和稳定变分法计算氦原子的极化率和色散系数

黄时中, 邓泽森, 张 勇

(安徽师范大学物理与电子信息学院, 芜湖 241000)

利用WBEPM模型和稳定变分法计算氦原子的极化率和色散系数

黄时中, 邓泽森, 张 勇

(安徽师范大学物理与电子信息学院, 芜湖 241000)

以最弱受约束电子势模型(WBEPM)理论为基础, 建立了计算氦原子多极动态极化率和相互作用色散系数的稳定变分方法. 导出了该方法中所涉及的矩阵元和线性方程组的解析表达式. 作为应用, 具体计算了基态氦原子的极化率和两体色散系数, 将计算结果与用其他方法所得到的结果进行了比较, 数据基本一致.

氦原子; WBEPM; 稳定变分方法; 极化率; 色散系数

1 引 言

随着激光冷却和囚禁技术的发展以及Bose-Einstain凝聚在若干碱土金属原子体系中的实现, 人们越来越关注碱土金属原子的极化率以及原子间相互作用色散系数的研究. 2007年, Mitroy 和 Zhang[1-3]发表3篇系列论文, 较全面地论述了碱土金属原子间相互作用色散系数的计算方法, 具体计算了若干激发态碱土金属原子与基态H 和 He的相互作用色散系数; 2009年, Yang和Tang等[4]以Tang-Toennies (TT)势模型为基础, 利用色散系数(C6、C8和C10)分析了基态Ca2以及Ca-RG (RG=He, Ne, Ar, Kr, Xe)的相互作用势; 2010年, Tang和Mitroy等[5]采用变分Hylleraas方法和半经验近似方法计算了Li+与惰性气体(He, Ne, Ar, Kr, Xe)之间的相互作用色散系数；2011年, Jiang和Kar等[6]采用屏蔽库仑势模型系统地计算了双电子正离子Li+、Be2+、B3+、 C4+、N5+和O6+的极化率; 2012年, Tang等[7]高精度计算了类氢离子基态的极化率以及H-H和H-He+相互作用色散系数.

尽管这些研究工作已取得了重要进展, 但目前的理论计算结果的精度还有待提高. 2008年, Masili等[8]将研究多光子电离问题中所采用的稳定变分方法引入到原子极化率和相互作用色散系数的计算中, 提出了计算原子极化率和相互作用色散系数的稳定变分方法, 具体计算了氢原子的极化率以及两体和三体相互作用色散系数, 得到了目前精度最高的氢原子极化率和相互作用色散系数, 并将其视为原子间相互作用色散系数的“精度标杆”.

2011年, Huang和Sun[9,10]以模型势理论为基础成功地将稳定变分方法推广应用到碱金属原子, 计算出了高精度的碱金属原子极化率、同核和异核碱金属原子间的两体和三体相互作用色散系数.

将稳定变分方法进一步推广应用到氦原子和碱土金属原子体系是一个有意义的设想, 实现此设想的一个关键问题是建立一个简洁而有效的模型势. 考虑到最弱受约束电子势模型(WBEPM)[11]在计算多电子原子的能级和跃迁几率[12-14]等方面都取得了很大的成功, 而且我们曾利用该模型势精确地计算过碳原子和铍原子[15,16]有关组态的精细结构能级, 因而很自然地想到也许可以将其应用到氦原子和碱土金属原子体系极化率和相互作用色散系数的计算工作中.

本文的主要工作就是以最弱受约束电子势模型(WBEPM)理论为基础, 建立计算氦原子多极动态极化率和相互作用色散系数的稳定变分方法(也就是将稳定变分方法进一步推广应用到氦原子体系). 导出该方法中所涉及的矩阵元和线性方程组的解析表达式, 具体计算基态氦原子的极化率和两体相互作用色散系数, 并将计算结果与用其他方法所得到的结果进行比较. 由于碱土金属原子的价电子构型与氦原子相似, 本文的工作也许可以为计算碱土金属原子极化率和相互作用色散系数提供一个新的途径.

2 氦原子体系的WBEPM近似

最弱受约束电子势模型(WBEPM)[11]理论的基本思想是将原子中的电子根据其活跃程度和被电离的能力划分为最弱受约束电子(WBE)和非最弱受约束电子(NWBE), 非最弱受约束电子和原子核被视为原子实部分, 最弱受约束电子在原子实的平均势场中运动, 因此多电子原子系统可以作为单电子系统处理. 基态氦原子的电子组态为1s2, 将其中的一个1s电子视为最弱受约束电子(WBE), 非最弱受约束电子(NWBE)和原子核被视为原子实部分, WBE在原子实的平均势场中运动. WBE所感受的势能函数可以表示为[11]

(1)

其中r是WBE与核之间的距离,Z′是有效核电荷数,l是WBE的角动量量子数,k是可调参数. 在势能函数(1)中, 第一项是电子与核之间的Coulomb势, 第二项是考虑原子实极化效应而设立的模型势. 采用原子单位, WBE所满足的Schrödinger 方程为

ψ=εψ

(2)

解此方程, 可以得到WBE的波函数

ψ(r,θ,φ)=R(r)Ylm(θ,φ)

(3)

式中Ylm(θ,φ)是通常的球谐函数,R(r)是径向波函数, 满足径向方程

(4)

其中

l′=l+k

(5)

求解方程(4), 可以得到径向函数R(r)的如下表达式

(6)

其中

n′=n+k

(7)

这里的n′和(4)式中的l′分别称为有效主量子数和有效轨道角动量量子数, 而n和l是WBE的主量子数和轨道角动量量子数. WBE的能量本征值和电离能分别是

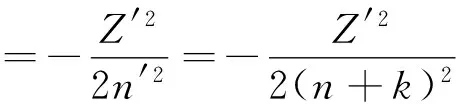
(8)

(9)

对于基态氦原子, 利用其电离能数据(见表1), 可以拟合出Z′、n′、k之值, 结果如下:

n′=0.997037,k=-0.002963,Z′=1.340596

(10)

表1 类氦原子基态的电离能(单位:eV)

Table1Ionizationenergies(ineV)ofHelium-likeatomsintheirgroundstates

ZIexpZIexp224.5873878205128.7375.640152156754153.8944226248.95259.37146236851.24246392.0886247481.77552.07162581418739.29293268828.04639953.9068279544.2101195.8222810289111465.134412911062.373121761.80393011865.151132085.97563112696.6048142437.62843213557.3315152816.91133163223.77653415367.3445173658.338335184120.6583617296.5633194610.869883718305.7166

3 氦原子体系的多极动态极化率

研究原子间的范德瓦尔斯相互作用色散系数的一个基础性工作是计算原子的多极动态极化率, 这是因为相互作用色散系数可以表示为原子的多极动态极化率的积分[17].

在最弱受约束电子势模型近似下, 氦原子的2L-极动态极化率αL(ω)可以表示为[8]

(11)

(12)

θ,φ)rL

(13)

引入中间态|λ〉, 其定义为

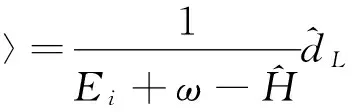
(14)

矩阵元(12)式可以写成

(15)

按照稳定变分方法[8], 先将上式改写成

(16)

再将中间态|λ〉按照一组已知函数{|μ〉}展开

(17)

(18)

得到待定系数aμ所满足的代数方程组, 解此方程组, 确定系数aμ.

将(17)式中的函数{|μ〉}取为斯莱特基, 中间态|λ〉展开为

(19)

其中

Φμl″(r)=Nμl″rl″+μ-1e-r

(20)

此处Nμl″是归一化因子, 且

(21)

设氦原子中WBE的初态为

|i〉=Rn′l′(r)Ylm(θ,φ) (l′=l+k)

(22)

利用(6)式以及(19)-(22)式, 完成(16)式中的积分, 可以得到双光子跃迁矩阵元的如下解析表达式

(23)

其中

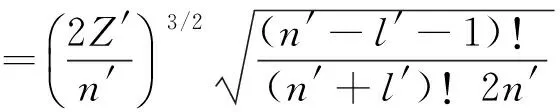
(24)

(25)

(26)

(27)

(28)

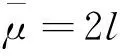
(29)

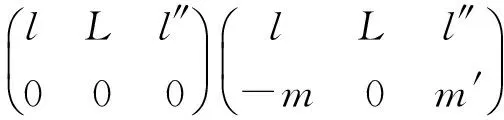
对于初态为基态的情形,l=0, 因而l″=L, 上述各式中的l″都取l″=L.

将(23)式代入变分原理(18)式, 得到参数aμ所满足的如下线性方程组

(30)

4 氦原子体系的两体色散系数

两个原子间的范德瓦尔斯相互作用可以表示为

(31)

其中R是两个原子核之间的距离;Cn是两体色散系数, 可以表示为原子的多极动态极化率的积分[17]

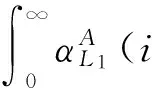
(32)

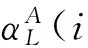
5 结果与分析

对于基态氦原子, 利用(10)式所给出的Z′、n′、k值, 我们应用Mathematica软件编程求解了M×M维线性方程组(30), 再按(23)和(11)式计算了基态氦原子的极化率. 计算过程中, 我们发现随着斯莱特基组数目的增加, 极化率的计算值迅速收敛并趋于稳定. 常用的前5个静态极化率(ω=0)的计算结果列于表2中的第一列, 表中同时列出了用其他方法所得到的结果.

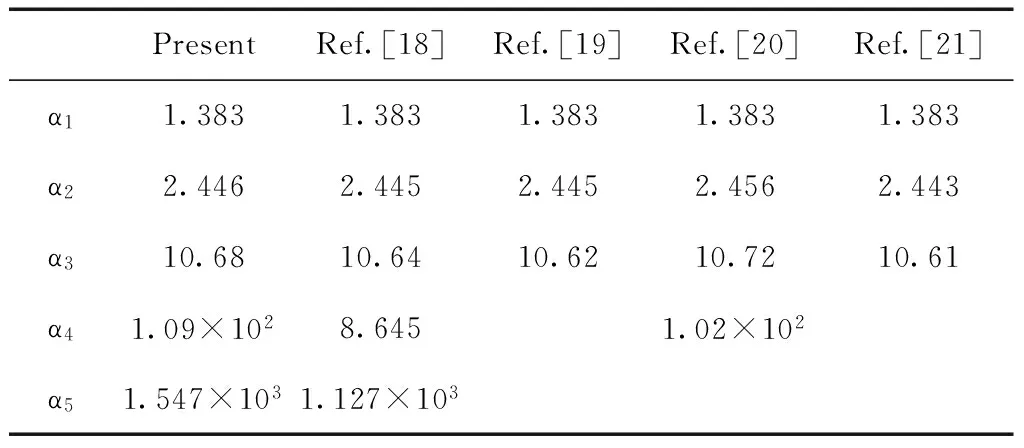
表2 基态氦原子的极化率(原子单位)

从表2可知, 对于低阶极化率αL(L=1,2,3), 本文的计算结果与文献[18]、[19]、[20]、[21]的结果很吻合. 而对于较高阶的极化率αL(L=4,5), 我们的结果与文献[20]的结果相符, 但与文献[18]的结果有比较明显的差异. 实际上, 文献[18]是利用氦原子波函数的渐近行为来分析氦原子的极化率的, 允许有一定的误差.

表3 基态氦原子间的色散系数(原子单位)

利用(32)式, 我们进一步计算了两个基态氦原子间的两体色散系数, 最重要的3个系数C6、C8和C10的计算结果列于表3中的第一列, 表中同时列出了用其他方法所得到的结果. 由表3可知, 本文所得到的色散系数结果与文献[18]、[20]、[22]、[23]的结果基本上是一致的, 这表明本文所提供的方法是有效的. 由于这一方法较为简捷, 而碱土金属原子的价电子构型与氦原子相似, 本文的工作也许可以为计算碱土金属原子极化率和相互作用色散系数提一个供新的途径. 我们将进行这方面的尝试.

[1]ZhangJY,MitroyJ.Long-rangedispersioninteractions.I.Formalismfortwoheteronuclearatoms[J]. Phys. Rev.A, 2007, 76: 022705.

[2]MitroyJ,ZhangJY.Long-rangedispersioninteractions.II.Alkali-metalandrare-gasatoms[J]. Phys. Rev.A, 2007, 76: 032706.

[3]MitroyJ,ZhangJY.Long-rangedispersioninteractions.IIIMethodfortwohomonuclearatoms[J]. Phys. Rev.A, 2007, 76: 062703.

[4]YangDD,LiP,TangKT.ThegroundstatevanderWaalspotentialsofthecalciumdimerandcalciumrare-gascomplexes[J]. J. Chem. Phys., 2009, 131: 154301.

[5]TangLY,ZhangJY,YanZC, et al.Long-rangedispersioncoefficientsforLi,Li+,andBe+interactingwiththeraregases[J]. J. Chem. Phys., 2010, 133: 104306.

[6]JiangZS,KarS,HoYK.Polarizabilitiesoftwo-electronpositiveionswithscreenedCoulombpotentials[J]. Phys. Rev.A, 2011, 84: 012504

[7]TangLY,ZhangYH,ZhangXZ, et al.Computationalinvestigationofstaticmultipolepolarizabilitiesandsumrulesforground-statehydrogenlikeions[J]. Phys. Rev.A, 2012, 86: 012505.

[8]MasiliM,GentilRJ.High-precisioncalculationofthedispersioncoefficientsofground-statehydrogenusingavariationallystableapproach[J]. Phys. Rev.A, 2008, 78: 034701.

[9]HuangSZ,SunQF.Higherordertwo-andthree-bodydispersioncoefficientsforalkaliisoelectronicsequencesbyavariationallystableprocedure[J]. J. Chem. Phys., 2011, 34: 144110.

[10]SunQF,HuangSZ.Multipolarpolarizabilitiesandtwo-bodydispersioncoefficientsforNabyavariationallystableprocedure[J]. J. Chem. Phys., 2011,135: 184106.

[11]ZhengNW,WangT,MaDX, et al.Weakestboundelectronpotentialmodeltheory[J]. Int. J. Quantum Chem., 2004, 98: 281.

[12]ZhengNW,ZhouT,YangRY, et al.Analysisoftheboundodd-parityspectrumofkryptonbyweakestboundelectronpotentialmodeltheory[J]. Chem. Phys., 2000, 258: 37.

[13]ZhengNW,XinHW.Successiveionizationpotentialsof4fnelectronswithin‘WBEPM’theory[J]. J. Phys.B: At. Mol. Opt. Phys., 1991, 24: 1187.

[14]ZhengNW,SunYJ,WangT, et al.Transitionprobabilityoflithiumatomandlithiumlikeionswithweakestboundelectronwavefunctionsandcoupledequations[J]. Int. J. Quantum Chem., 2000, 76: 51.

[15]MaK,HuangSZ,YuJM, et al.CalculationofRydbergenergylevelsforCIatom[J]. J. At. Mol. Phys.(原子与分子物理学报), 2009, 26: 39(inChinese)

[16]HuangSZ,LiuF,MaK,CalculationofRydbergenergylevelsforberylliumatom[J]. J. At. Mol. Phys.(原子与分子物理学报), 2010, 27: 637(inChinese)

[17]DalgarnoA,DavisonWD.ThecalculationofVanderWaalsinteractions[J]. Adv. At. Mol. Phys., 1966, 2: 1.

[18]PatilSH,TangKT.Asymptoticmethodforpolarizabilitiesanddispersioncoeffcients:Withapplicationstohydrogenandheliumsystems[J]. J. Chem. Phys., 1997, 107: 3894.

[19]YanZC,BabbJF,DalgarnoA, et al.VariationalcalculationsofdispersioncoefficientsforinteractionsamongH,He,andLiatoms[J]. Phys. Rev.A, 1996, 54: 2824.

[20]SpelsbergD,LorenzT,MeyerW.DynamicmultipolepolarizabilitiesandlongrangeinteractioncoefficientsforthesystemsH,Li,Na,K,He,H-,H2,Li2,Na2,andK2[J]. J. Chem. Phys., 1993, 99: 7845.

[21]KoideA,MeathW,AllnattAR. Ab initioevaluationofmultipoledispersionenergiesandproperties[J]. J. Phys. Chem., 1982, 86: 1222.

[22]GutowskiM,VerbeekJ,VanLJH, et al.Theimpactofhigherpolarizationfunctionsonsecond-orderdispersionenergy,partialwaveexpansionanddampingphenomenonforHe2[J]. Chem. Phys., 1987, 111: 271.

[23]ThakkarAJ.Anewgeneralizedexpansionforthepotentialenergycurvesofdiatomicmolecules[J]. J. Chem. Phys., 1981, 75: 4496.

Calculation of multipole polarizability and dispersion coefficients for helium by WBEPM and variationally stable procedure

HUANG Shi-Zhong, DENG Ze-Sen, ZHANG Yong

(College of Physics and Electrical Information, Anhui Normal University, Wuhu 241000, China)

Based on the weakest bound electron potential model (WBEPM) theory, method of calculating the multipole dynamic polarizability and dispersion coefficients for Helium by a variationally stable procedure is established. The matrix elements and a group of linear equations, involving in this approach, are derived analytically. As an application, the polarizability and two-body dispersion coefficients between Helium atoms in their ground states are calculated concretely and are compared with those calculated previously by other procedures. It is found that the calculated results are consistent with those of others.

Helium; WBEPM; Variationally stable procedure; Polarizabiliy; Dispersion coefficients

2014-09-06

安徽省自然科学基金项目(11040606M15); 国家自然科学基金专项基金项目(11047019)

黄时中(1958—),男, 安徽宿松县人, 理学博士, 教授, 主要从事原子结构理论和原子间相互作用理论研究. E-mail: huangsz@mail.ahnu.edu.cn

103969/j.issn.1000-0364.2015.10.003

O562.4

A

1000-0364(2015)05-0728-05