基于DKPCA的聚合釜故障诊断研究
2015-03-22高淑芝
高淑芝, 赵 娜
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
基于DKPCA的聚合釜故障诊断研究
高淑芝, 赵 娜
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
针对聚合釜聚合生产聚氯乙烯过程的故障种类较多、故障类型复杂等特点,同时生产过程存在严重的非线性、动态性,提出一种基于DKPCA的故障诊断算法.过程中分别采用主元分析、核主元分析和动态核主元分析分别对PVC聚合过程进行故障诊断,其中主元分析和核主元分析的错报率较高,而动态核主元分析对PVC聚合过程能够得到较好的诊断结果,从而可以对实际的PVC聚合生产过程进行监测.
PVC聚合; 故障诊断; 动态核主元分析
聚氯乙烯树脂(PVC)是重要的有机合成材料,又是具有多种用途的化工产品.PVC树脂作为一种化工产品,生产过程故障产生机理复杂,迫切需要提高系统生产的可靠性和安全性.为此,对于生产PVC树脂过程中的故障研究,一直是专家研究的重要问题[1-2].目前主元分析在化工过程故障诊断中应用极为广泛.由于生产PVC树脂过程的大量数据存在严重的非线性、强耦合性、动态性[3-4],导致传统的主元分析(PCA)对其过程的监测误报率漏报率过高,因此,国内外学者分别对其进行了一系列的改进,如核主元分析(KPCA)、动态主元分析(DPCA)等.在针对动态性上Ku等在1995年提出动态主元分析[5],Viliam Makis 等人将 DPCA 方法应用到石油状态检修模型中[6],一系列的仿真结果表明 DPCA 方法能准确对故障进行检测.在针对非线性问题上, Kramer提出了基于自联想神经网络的非线性主元分析方法[7],Dong和McAvoy提出了基于基元曲线和神经网络的非线性PCA方法[8],近年来,引入核函数的核主元分析(KPCA)方法得到迅速发展,Lee和Qin对其进行了研究[9],研究结果显示,在对化工过程的监测过程中改进的主元分析方法,都要好于传统的主元分析.
在分析了PVC树脂生产数据的特点后,发现数据中存在严重的非线性、动态性,因此本文采用一种复合的方法——动态核主元分析(DKPCA),弥补了传统主元分析能力不足的缺陷.
1 PVC聚合反应介绍
以某单位PVC树脂的生产过程为研究对象,聚合反应过程如图1所示.参与反应的单体、引发剂、分散剂等物料加入到聚合釜中,单体在引发剂作用下,最终生成聚合物,聚合过程中不断放热,使聚合釜内的温度不断提升,反应愈加剧烈,最终导致物料流量失衡,影响聚合产物质量.所以,在聚合釜内加入搅拌系统,并适时注入冷却水来平衡聚合釜内温度.待反应结束后,加入终止剂,终止聚合反应.
从PVC聚合的工艺流程中发现,影响聚合产物质量的指标较多,任何一个变量超标,都可导致产品质量失控.因此,对聚合过程中的质量指标进行实时监测,以确保在产品质量改变时能对其进行及时准确的诊断.经对比研究,最终确定选取10个变量作为研究对象,它们分别是:釜内温度、釜内压力、搅拌电流、注入水流量、密封水流量、夹套水流量、档板水流量、冷却水进口温度、夹套水出口温度、档板水出口温度.
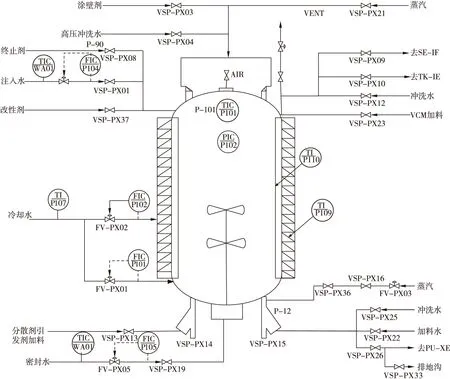
图1 聚合反应工艺过程
2 PCA与KPCA的基本原理
2.1 PCA基本原理
主元分析基于数据建立系统统计模型,首先取一段正常工况下的数据集Xn×m(n为采样点个数,m为变量个数)建立统计模型.矩阵X可以表示为n个向量的外积之和,即:
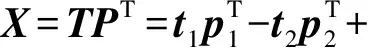
(1)
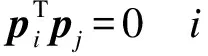
ti=Xpi
(2)
ti的大小决定了数据矩阵在负荷向量上的覆盖程度,最大得分向量定义为第一主元,以此类推,确定第二主元、第三主元、….第n主元.数据X的变化主要体现在前几个主元上,数据在后面的几个负荷向量上的投影主要是由噪声引起的,用矩阵E表示,即:
(3)
一般采取累积贡献率原则,确定主元个数.k为选取主元个数,E为误差矩阵,将E忽略通常能起到清除测量噪声的目的.待主元个数确定好后,通过这两个子空间建立PCA统计模型.常用的PCA统计量有HotellingT2和Q统计量,其检测值如下:
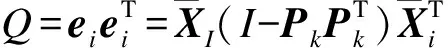
(4)
统计量指标的控制限计算如下:
QL=a(b+cza)d.
(5)
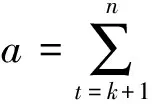
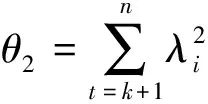
T2统计量的大小的定义为:
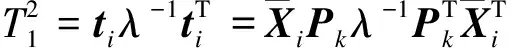
(6)
T2统计量指标的控制限计算如下:
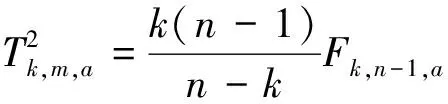
(7)
a是显著性水平,数据采样次数为n,变量个数为m.k为数据阵的主元个数,Fk,n-1,a是检验水平为a自由度为(k,n-k)条件下的分布临界值.当统计量没有超过控制限范围,则系统表示无故障;当统计量超出了控制限范围,则说明系统中存在着一定故障.
2.2 KPCA基本原理
KPCA 的基本思想是通过非线性映射φ把输入空间映射到特征空间F上.其协方差矩阵可按下式计算:
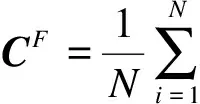
(8)
确定CF的特征向量,就能够求得空间F中的主元,CF所表示的特征向量与输入空间的PCA方法直接相关.
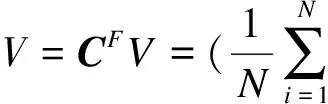
(9)
即在λ≠0的条件V的所有解都可以由φ(x1),…,φ(xn)所表达出.因此λv=CFv等价于:
λ〈φ(xk),V〉=〈φ(xk),CFV〉,
k=1,…,n.
(10)
存在一个系数ai(i=1,…,N),使得:
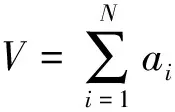
因此,结合(10)式,可以得出:
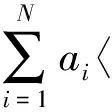
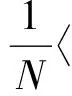
〈φ(xj),φ(xi)〉,
(11)
同时,定义一个N×N矩阵,K∈RN×N
[K]ij=Kij=〈φ(xi),φ(xj)〉,
(12)
因此,等式(10)可以化简为:
λNa=Ka,a=[a1,…,aN]T.
(13)
在使用KPCA方法之前,首先要对复杂的高维空间进行均值中心化处理.可通过下式取代核矩阵K来实现[10].
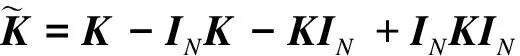
(14)
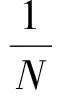
因此,向量x所求得的主元t能够通过φ(x)映射到F中的特征向量Vk上,其中k=1,…,p.
tk=〈Vk,φ(x)〉=
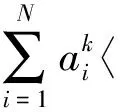
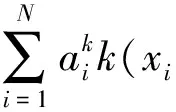
(15)
可以发现:KPCA通过引入k(x,y)=〈φ(x),φ(y)〉这个核函数,避免了进行复杂非线性映射计算和计算特征空间上的点积.如何选择核函数完全决定φ和特征空间F,这里选择径向基核函数:k(x,y)=exp(-‖x-y‖2/σ).
3 基于动态核主元分析的故障检测
传统的PCA方法应用具有局限性,所以针对这样的动态非线性系统应研究一种能够同时捕捉过程数据之间的动态性和非线性的新方法,即动态核主元分析方法(DKPCA).
DKPCA故障诊断方法的核心是通过用前面的数据对每个观测变量进行扩充,构建含有前S个时刻观测值的增广矩阵[11],增广矩阵如下:
(16)
通过对扩展时间序列后的上述增广数据矩阵应用核函数主元分析进行故障的检测.DKPCA检测步骤如下:
步骤一:获得训练数据X和测试数据Xnew,并对X进行标准化处理;
步骤二:确定滞后S的大小,构造增广矩阵;
步骤三:通过径向基核函数完成非线性变换,并求特征值与特征向量;
步骤五:按上述步骤确定测试数据Xnew的动态核主元;
4 仿真实例研究和结果
首先,分析聚合工艺的特点,分析发现影响聚合产物质量指标的过程变量有10个,采集某化工厂正常聚合过程下的50组数据作为训练样本矩阵X50×10,采集200组在线观测数据作为测试数据.每5 min采样一次,在第51组模拟引入故障1,即温度的升高.在第125组数据中,模拟引入故障数据2,即使搅拌电流提高15 %.
根据上述过程,分别用传统主元分析,核主元分析,动态核主元分析对PVC聚合过程进行故障诊断.诊断结果如图2、图3、图4所示.
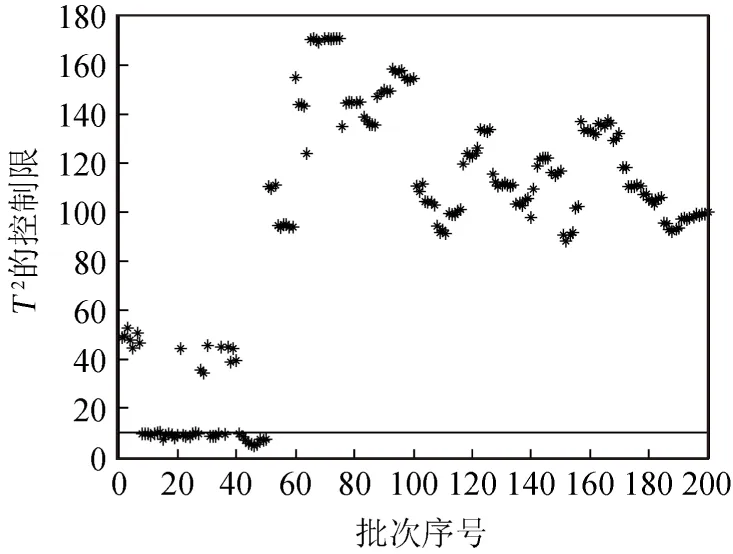
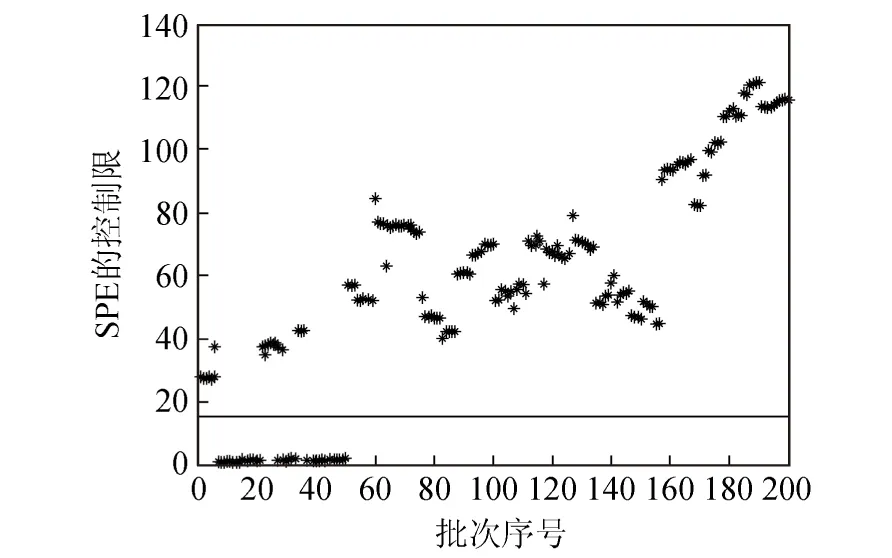
图2 主元分析T2和SPE故障检测结果
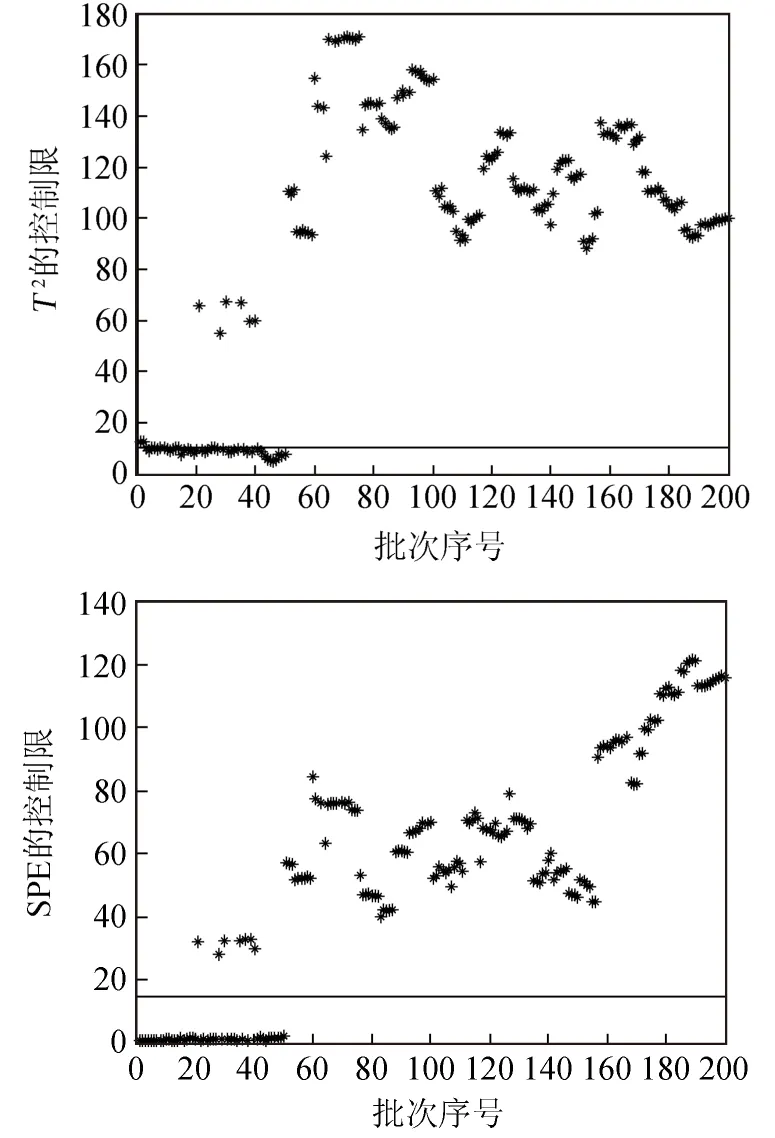
图3 核主元分析T2和SPE故障检测结果
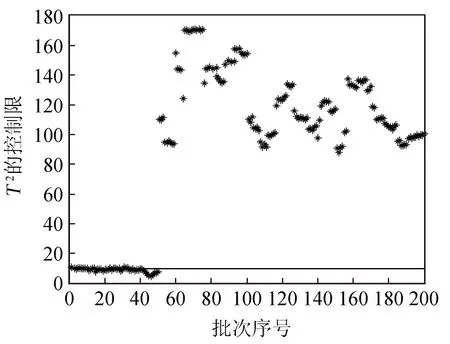
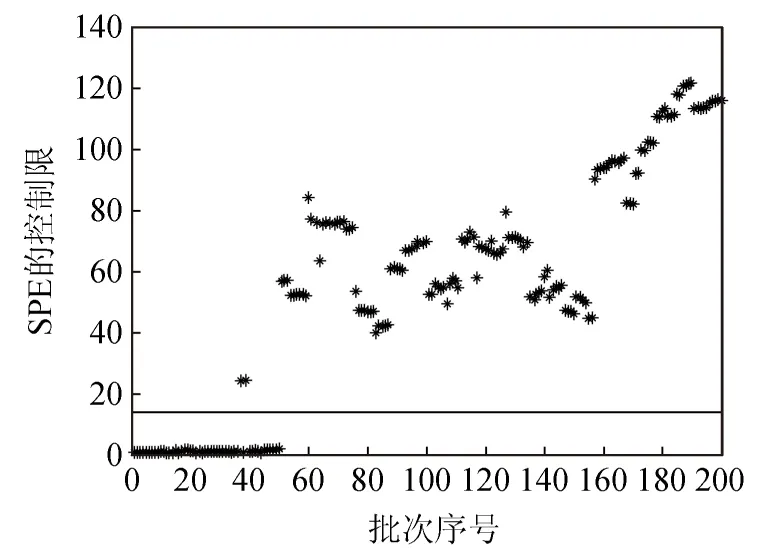
图4 动态核主元分析T2和SPE故障检测结果
为了能更清楚的判断出哪种诊断效果更突出,通过对比其误报率的高低来判断,误报率越低证明此种方法应用在聚合釜故障诊断生产中越合适.诊断结果如表1所示.

表1 三种诊断方法的误报率
无论从仿真图中还是表格中清晰地发现,传统的主元分析与核主元分析在50点采样前,有多处超过控制限,误报率相当严重,导致工作人员的错误判断.而动态核主元分析的故障检测中,只有2处误报,并且引入故障的阶段,明显超出控制限,从而提高故障诊断的效率.
5 结 论
在传统主元分析和核主元分析的基础上引入了数据的动态性原理,引入动态核主元分析方法,用来对动态性和非线性较强的聚合釜过程进行故障检测.仿真结果表明,该方法能实时的监测聚合过程中变量的变化,对聚合过程中的故障更为敏感,减少了错误报警的概率,结果说明,该方法可以应用到对聚合釜的故障处理,同时,对一般的具有动态非线性的化工过程,也有一定的适用性.
[1] 高淑芝,高宪文,王介生,等.基于改进差别矩阵属性约简的聚合釜粗糙集-神经网络故障诊断[J].化工学报,2011,62(3):759-765.
[2] 高岩,杨慧中.一种主元分析方法在聚合生产过程故障监测与诊断中的应用[J].江南大学学报:自然科学版,2005,4(4):352-356.
[3] 王婷.基于2D-DKPCA的故障检测方法在青霉素发酵中的应用[D].沈阳:东北大学信息科学与工程学院,2008:34-44.
[4] 李磊,朱建宁,侍洪波.基于多尺度动态核主元分析的化工过程故障检测[J].化工自动化及仪表,2008,35(4):23-26.
[5] Ku W F,Storer R H,Georgakis C.Disturbance Detection and Isolation by Dynamic Principal Component Analysis[J].Chemometrics and Intelligent Laboratory Systems,1995,30(1):179-196.
[6] Makis V,Wu J M,Gao Y.An Application of DPCA to Oil Data for CBM Modeling[J].European Journal of Operational Research,2006,174(1):112-123.
[7] Kramer M A.Nonlinear Principal Component An-alysis Using Autoassoeiative Neural Networks[J].The American Institute of Chemical Engineering Journal,1991,37(2):233-243.
[8] Dong D,McAvoy T J.Nonlinear Principal Component Analysis-based on Principal Curves and Neural Networks[J].Computers and Chemical Enginee-ring,1996,20(1):65-78.
[9] Lee J M,Qin S J,Lee I B.Fault Detection of Non-linear Processes Using Kernel Independent Component Analysis[J].The Canadian Journal of Chemical Engineering,2007,85(4):526-536.
[10]文道松.基于改进主元分析的工业过程故障检测与诊断[D].哈尔滨:哈尔滨理工大学自动化学院,2011:24-36.
[11]石怀涛,刘建昌,丁晓迪,等.基于混合动态主元分析的故障检测方法[J].控制工程,2012,19(1):148-150.
Fault of Polymerization Reactor Based on DKPCA Algorithm
GAO Shu-zhi, ZHAO Na
(Shenyang University of Chemical Technology, Shenyang 110142, China)
For the characteristics of PVC polymerization process that fault types are varied and complex,while the production process is serious nonlinear and dynamic,a fault diagnosis algorithm is proposed based on DKPCA.In the process component analysis,kernel principal component analysis and dynamic kernel principal component analysis are used to carry out fault diagnosis on the PVC polymerization process.PCA and KPCA misstatements rate is serious,and dynamic kernel principal component analysis for PVC polymerization process fault diagnosis has better diagnostic result.The actual process for the production of PVC polymerization can be monitored.
PVC polymerization; fault diagnosis; dynamic kernel principal component analysis
2013-11-08
赵娜(1988-),女,辽宁沈阳人,硕士研究生在读,主要从事聚合釜过程故障诊断方面的研究.
高淑芝(1968-),女,辽宁沈阳人,教授,博士,主要从事复杂建模过程的控制优化方面的研究.
2095-2198(2015)02-0178-05
10.3969/j.issn.2095-2198.2015.02.018
TQ316.3
A
