扇形流道内Stokes流动特性的数值模拟

王宗勇, 赵家瑜, 吴剑华, 王舒婷

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

扇形流道内Stokes流动特性的数值模拟

王宗勇, 赵家瑜, 吴剑华, 王舒婷

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

针对低雷诺数下外壁旋转的扇形截面流道内的流动特性进行数值模拟，得到不同扇形角度下的速度、涡量及流函数的分布规律.研究结果表明:在低雷诺数下扇形流道内的三维Stokes流可以分解为两个二维流动，即压力降推动的轴向流及圆弧外壁旋转诱发的扇形腔内截面流；流道内的轴向速度和周向速度与扇形角平分线成对称分布关系，而径向速度成反对称关系；随着扇形角度的减小，流道内会出现多个涡流区域，各涡流区域内的速度场、涡量场及流函数均具有自相似性，说明外壁旋转的扇形流道内的流体具有混沌运动特征；雷诺数相同的情况下，流道内的涡量随着扇形角度的减小而增大，表明小角度扇形截面流道有利于流体的混合.

Stokes流； 螺旋流； 低雷诺数； 速度场； 涡量场

螺旋流是一种特殊的、规则的涡旋运动，是化学工程中广泛存在的一种流动现象.螺旋流被广泛应用的原因是流体在螺旋流动过程中会形成垂直于主流方向的二次流或混沌流，能够起到强化流体混合或传热的作用.工程上形成螺旋流的方式主要有两种:一种是流体在螺旋或扭旋通道内整体围绕某一回转中心螺旋流动，如螺旋盘管或Kenics型静态混合器内的流动；另一种是流体在压力推动向前流动的过程中由于外壁的旋转作用而形成螺旋流，如分隔管混合器[1](partitioned pipe mixer)内流体的流动.

分隔管混合器(PPM)是Khakhar等人提出的用于黏性流体混合的动态混合装置，该混合器是广泛使用的Kenics混合器的原型.其结构是在长圆管内部插入一系列彼此垂直的平板，利用圆管的旋转实现流体的混沌混合，如图1所示.Khakhar等[1]利用近似的三维速度分量,研究与横截面流型相关的混合、停留时间分布及流线拉伸率.Meleshko等[2]得到了PPM横截面内速度场的精确解析解，该解对于流体流动的描述相对于以前的近似解更为准确，混合模式更加接近于Kusch和Ottino的实验结果[3].Mizuno和Funakoshi[4]对PPM进行一般化处理，即相邻板的长度比和夹角是可以变化的.他们对这种形式混合器的流体混合进行了研究，结果表明:改变相邻板长度比和夹角可以使混沌区域占据整个流体空间.后来他们又对一般形式的PPM的混沌混合性质及效率进行了深入研究，发现流体单元被分隔板前缘分开后的拉伸非常有助于流体混合[5].根据Mizuno和Funakoshi的结论可知:改变PPM的结构,特别是增加分隔板的数量能够显著提高PPM混合器的混合效果.为此，本文提出了一种新型的PPM混合器，可将其表示为IPPM.这种混合器每个横截面上具有两块平板，两块平板可以相互垂直也可以是其它任意角度，这两块平板构成一个混合单元，相邻混合单元相互错开90°，即前一混合单元两块平板夹角的平分线与下一混合单元对应夹角的平分线垂直，如图2所示.

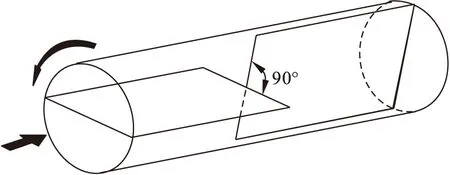
图1 PPM结构示意图

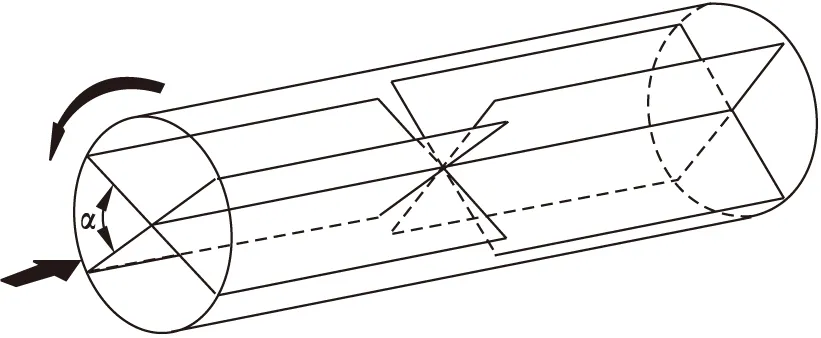
图2 IPPM结构示意图

IPPM将混合管分隔成4个扇形通道，流体在相应的扇形通道内螺旋流动，同一流道内的流体在流到下一混合单元时被一分为二，分别进入不同的流道，在宏观上实现了流体的分布混合，更为重要的是流体在扇形截面流道内确定性流动条件下还能够实现混沌混合，该混合机理对于高黏度、低流速的流体混合强化具有重要意义.

除前面提到的外壁旋转的扇形截面直流道之外，工业上多种单元设备还具有扇形截面螺旋流道，如Kenics型静态混合器、带有半管夹套的反应釜等，虽然这种流动结构与本文的研究对象完全不同，但从流体特性上来看两种之间存在一定程度的近似性和关联性.扇形截面螺旋流道的相关研究结论对于本研究具有较大借鉴价值.

王宗勇[6]对多流道螺旋静态混合器的扇形通道内的浓度场进行了分析，得到了混合器通道数的选用规律.龚斌[7]利用实验及数值模拟方法对Kenics混合器内湍流状态下的速度场进行分析，得到了元件长径比对湍动能和各速度分量的影响规律.李雅侠[8-11]对螺旋半圆管夹套内层流和湍流的流动特性及换热特性进行了研究，得到了雷诺数与半圆管夹套内传热系数的相互关系.刘雯[12]对圆管内螺旋纽带在高Reynolds数时引发的涡流流场进行了分析，得到了短螺旋纽带引发的螺旋涡特性及Reynolds数对螺旋涡的影响规律.

许多学者对于二维楔形域或环形域的Stokes流动特性进行了研究.Moffatt[13]通过流函数证明了涡流在楔形角小于临界角时的存在性，得到了楔形内涡流的分布规律.Liu和Hills[14-15]在Moffatt研究基础上,证明了涡流在圆弧形内的存在性,并绘制了流函数与涡流的关系图.Krasnopolskaya进一步研究了楔形内涡流的存在性，分析了二维Stokes流的流动特性,并用解析方法得到了楔形内涡流分布规律[16-17].Galaktionov和Meleshko等利用无穷级数理论解析研究了半圆管内Stokes流动特性，获得了轴向速度封闭表达式[18].

以上研究均是针对某一特定角度的扇形截面流道或楔形域的研究，针对不同角度的扇形截面流道的流动特性的对比研究还鲜有报导.本文研究不同角度扇形流道内的流体速度分布，以及扇形角度对流动特性的影响规律，为进一步研究IPPM 的混沌混合特性及其结构优化奠定基础.

1 数值模拟

1.1 物理模型

扇形截面流道由一对相交的矩形平板和一个圆弧柱面构成，圆弧柱面与两平板正交并且平板交线为圆弧柱面的轴线.圆弧柱面绕着轴线以恒定的角速度转动，相交平板静止不动.进入扇形截面流道的流体在压力梯度的作用下沿着轴线方向向前流动，同时在圆弧外壁的旋转带动下产生径向及周向流动.

为了便于对扇形截面流道的流动特性进行分析，在流动区域内建立圆柱坐标系.两平板的交线为z轴，方向为流体轴向流动方向；角度坐标θ起始位置(θ=0)位于扇形截面夹角平分线上，外壁旋转方向的角度坐标为正，径向坐标r由坐标原点指向圆弧外壁任意位置，圆弧外壁半径为R，扇形截面夹角为α，外壁旋转角速度为ω，如图3所示.

为保证流体在轴向充分发展，取扇形流道长L=1 m,半径R=0.05 m，扇形流道夹角α分别取120°、90°、60°、30°进行对比研究.

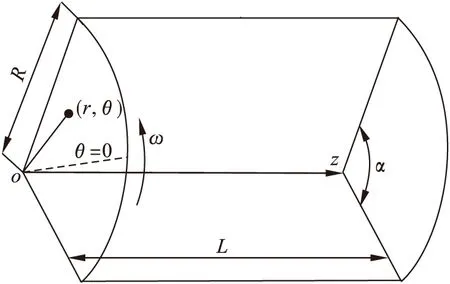
图3 扇形流道的圆柱坐标系

应用流体力学软件Fluent进行模拟计算，以水为工作介质，采用层流稳态模型，均匀流速入口，充分发展出口.计算网格采用非结构六面体网格，通过网格独立性实验，确定面网格间距为0.4 mm，体网格间距为1 mm.压力和速度的解耦采用SIMPLEC算法，收敛残差均取小于1.0×10-5.

1.2 边界条件

2 扇形流道内的速度分布

为便于问题的分析，对流道内的流体各方向速度分量及坐标进行无量纲化，分别为r′=r/R,z′=z/R,θ′=θ,u′=u/ωR,v′=v/ωR,w′=w/ωR.带有上角标的各符号为无量纲后的量，u，v，w分别表示轴向、径向及周向速度分量.取流动充分发展截面z=0.8 m(z′=16)的模拟结果分析扇形角度对流动特性的影响.

由图4可以看出:流体各方向速度分量以扇形截面夹角平分线为轴呈现对称分布状态，这主要决定于流道结构及边界转动条件的对称性.

各角度扇形截面内的轴向速度等值线与扇形边壁形状相似，越靠近边壁相似度越高,并且速度梯度较大,而靠近扇形截面形心位置的速度等值线趋向于圆形，速度值变大,但速度梯度减小.这种轴向速度的分布特点表明:低雷诺数下,圆弧外壁的旋转对流体的轴向运动可以忽略不计，轴向速度分布规律取决于各边壁轴向固定不动对流体的黏滞阻碍作用.由图4还可看出:随着扇形角度的增大，轴向速度中心及速度最大位置逐渐偏离圆弧边壁，沿着对称线向顶点方向靠拢.

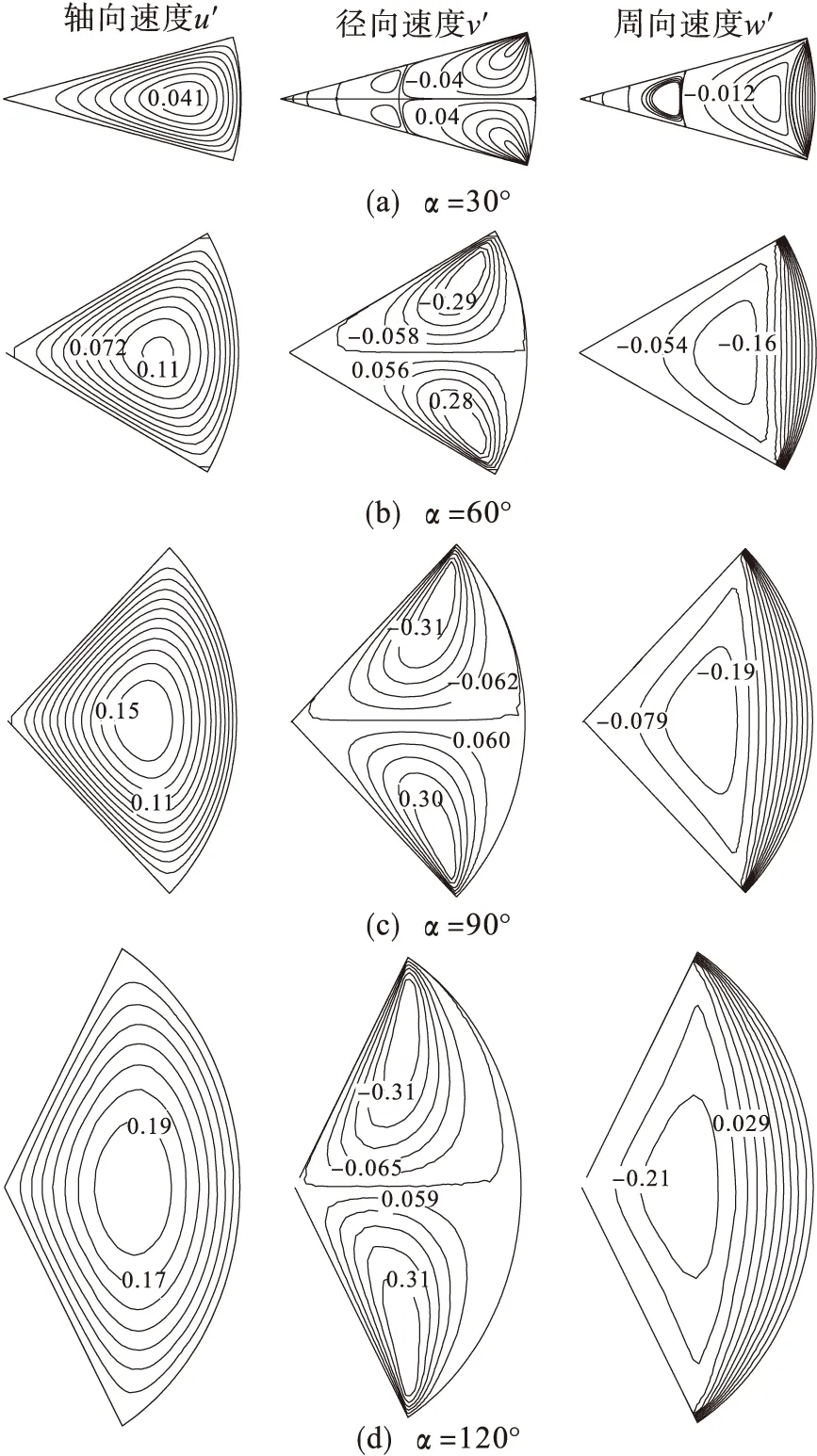
图4 扇形流道的速度等值线

径向速度等值线虽然也呈现对称状态，但其分布规律与轴向速度截然不同，不再是与边壁近似的形状，而是一种卵形并且具有一个唯一的交点，处于圆弧边壁与平面边壁相交的边角处，此外对称线两侧的径向速度符号相反，实际上径向速度分布是一种反对称状态，说明流道内的流体在圆弧外壁旋转的带动下，对称线一侧流体由顶点流向圆弧，而另一侧流体由圆弧流向顶点.由图4还可看出:当扇形流道角度较小(α=30°)时，径向速度明显出现了几个环形区域，各区域内的速度等值线形状具有一定的相似性，但对称线一侧相邻区域的速度方向相反且相差多个数量级(由于图形较小没有显示数值).

周向速度等值线形状由两部分构成:一个是与旋转外壁形状类似的圆弧线，另一个是与扇形通道三个边角点连线构成的三角形类似的封闭曲线.这两部的流体运动方向相反，其方向是以流体相对于流道轴线的旋转方向来定义的，若是逆时针(圆弧外壁旋转方向)为正，反时针则为负.与径向速度特点一样，当扇形流道角度较小(α=30°)时，周向速度等值线也出现了几个环形区域，各区域的径向宽度随着远离圆弧边壁而迅速减小，相邻区域内流体的转动方向相反，且转动速度相差几个数量级.

径向速度和周向速度的分布规律表明：圆弧边壁的旋转带动了其附近流体按相同方向旋转流动，但这种流动会受到两侧平面边壁的阻碍作用，这种阻碍作用会随着扇形角度的减小而增大，因此,会将旋转流体限定在一定的区域范围内，这个区域除了原来具有的三个壁面边界之外，还有一个与圆弧边壁对应的虚拟圆弧边界，这个虚拟边界在其内侧旋转流体(图中虚拟边界右侧流体)带动下也旋转运动，只不过与实际圆弧边壁旋转方向相反，大小相差几个数量级而已.虚拟圆弧边界左侧的流体在虚拟圆弧带动下也会形成旋转流动，这个流动同样会受到平面边壁的阻碍作用，形成第二个旋流区域，依次类推就出现了多个旋流区域.

3 扇形截面的流函数

外壁旋转的扇形流道内的流体流动尽管属于三维流动，但是经前面的分析可知在低雷诺数下，该三维流动实际上可分解为两个二维流动，即压力降引起的轴向流动及外壁旋转诱导的横截面内流动.在定常情况下，对于不可压缩流体而言，流动截面的流函数代表了流体的流线及运动轨迹线.扇形截面的流函数如图5所示.

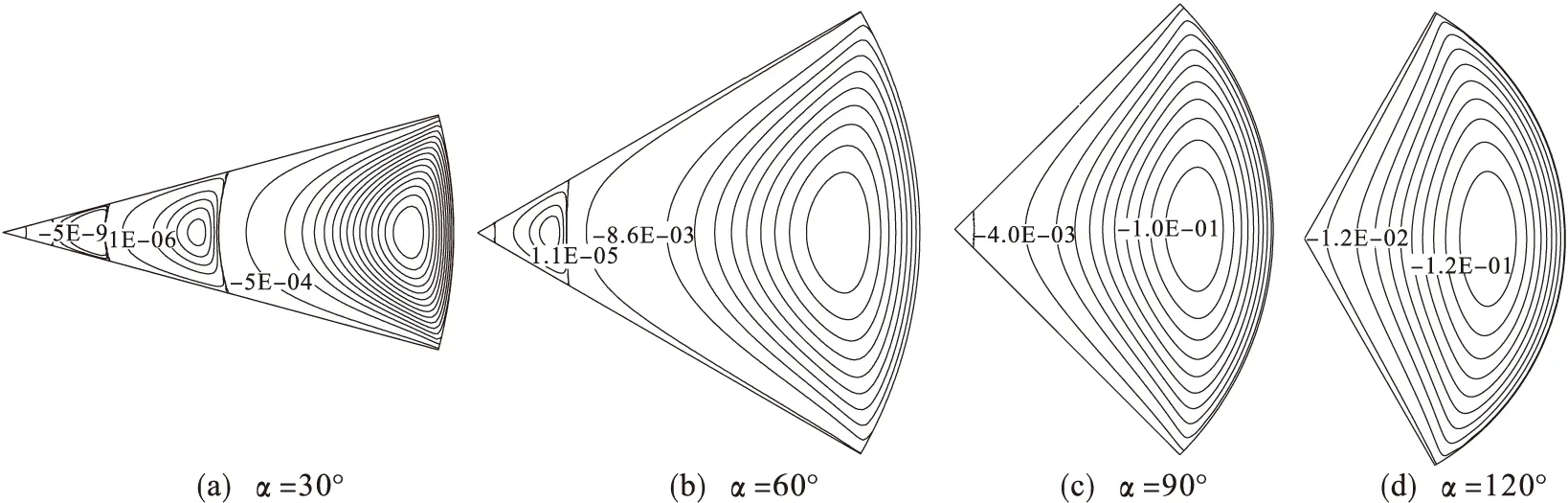
图5 扇形截面的流函数

分析图5中各角度扇形截面的流函数等值线图可知:横截面内的旋转流动主要集中在靠近圆弧外壁的一定区域内，圆弧外壁附近的流函数梯度明显大于其它部位，说明该区域流体的环流流量大.随着扇形角度的减小，扇形截面内明显出现了多个涡流区域，外壁旋转所引起的主涡流区域的径向宽度显著变小，而靠近主涡流区域的其它诱导涡流区域的宽度显著增大，相临涡流区域内流体的转动方向相反，这与前面速度分布所得结论一致.随着径向距离的减小，各涡流区域内的环流流量急剧衰减.各涡流区域的中心均靠近其右侧圆弧边界，说明各区域的运动能量均来自于各自的圆弧边界.另外通过观测扇形截面内相邻涡流区域内流函数等值线的分布特点，可以看出它们具有自相似性，这也是混沌运动的一个显著特征.大量的理论及研究结果表明:流体的混沌运动对于低雷诺数下黏性流体的混合具有重要的作用.

4 扇形截面的涡量场

涡量是描写流体涡旋运动常用的物理量，可通过对流体速度场取旋度来确定.流体是否有旋取决于流体微团本身是否旋转，而与流体微团的运动轨迹没有必然的联系，同时也不决定于流体的流动状态是层流还是湍流.研究结果已经表明:流体出现涡流能够增强流体的混合能力，特别是在层流状态下增强效果更为明显.

为分析不同角度扇形流道的涡流特征，绘制3个角度扇形流道的轴向涡量等值线图，如图6所示.纵观各等值线图可以看出:扇形截面内靠近流道边界处的涡量较大，而随着向截面形心的靠近涡量变小，说明流体轴向涡量与流体径向速度和周向速度的大小没有必然联系，而仅与两者变化梯度的差值有关.对比各角度下的轴向涡量等值线图还可看出:在雷诺数相同的情况下，扇形角度增大涡量值反而变小，说明流道的结构对流体的涡旋具有显著影响，从流体涡流强度角度而言，较小的扇形角度反而有利于流体混合.由此可见,将原始的PPM改进为本文所提出的IPPM,对提高流体混合效果具有一定的理论依据.

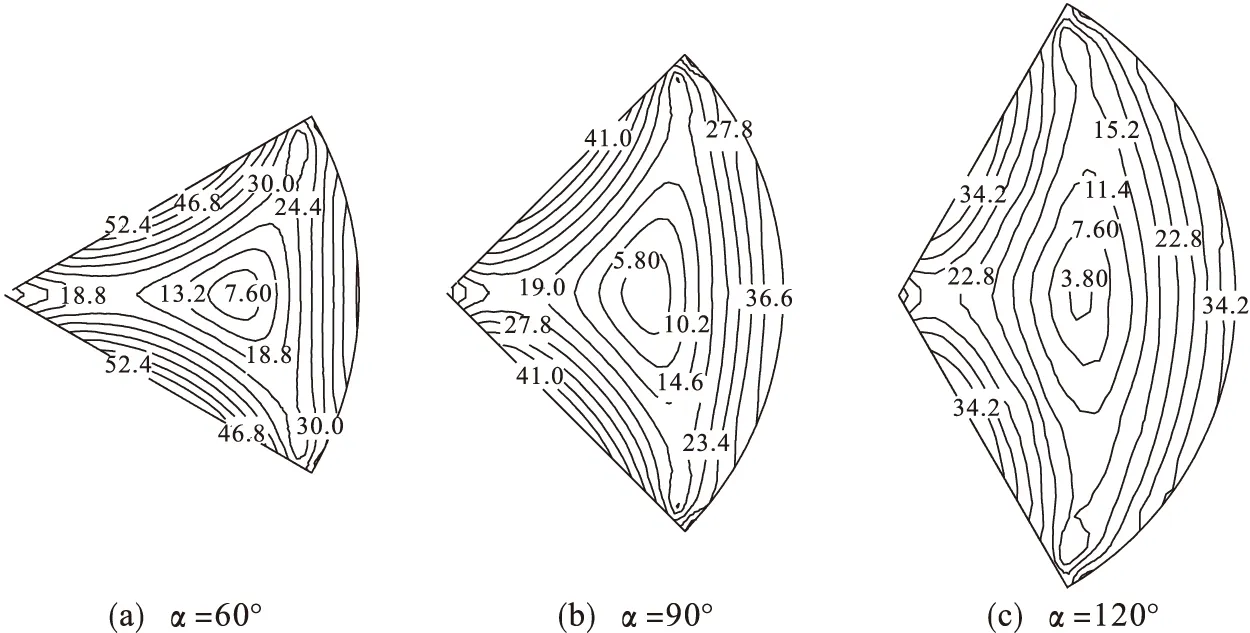
图6 扇形截面的轴向涡量

5 结 论

(1) 外壁旋转的扇形截面流道在低雷诺数下的三维Stokes流可以分解为两个二维流动，即压力降推动的轴向流及圆弧外壁旋转诱导的扇形截面腔内流，该结论为解析研究扇形截面流道内的速度分布提供了可能和依据.

(2) 轴向速度等值线形状与扇形流道结构具有一定的相似性，表明流道外壁的黏滞作用是形成轴向速度分布特征的主要原因.径向速度在靠近平面边壁附近较大，而接近对称轴位置偏小，这样的结果有利于低速区的流体混合及传热.周向速度在圆弧外壁附近较大且与外壁旋转方向相同，表明外壁旋转是形成周向流动的原动力.

(3) 随着扇形角度的减小，流道内会出现多个涡流区域，并且圆弧外壁处的主涡流区域的径向宽度会随着扇形角度的减小而减小，而其它诱导涡流区域则会相应增大.

(4) 扇形截面内的各涡流区域内的速度场、涡量场及流函数均具有自相似性，表明外壁旋转的扇形流道内的流体具有混沌运动特征.

(5) 雷诺数相同的情况下，流道内的涡量随着扇形角度的减小而增大，说明小角度扇形截面流道有利于流体的混合.

[1] Khakhar D V,Franjione J G,Ottino J M.A Case Study of Chaotic Mixing in Deterministic Flows:The Partitioned-pipe Mixer[J].Chemical Engineering Science,1987,42(12):2909-2926.

[2] Meleshko V V,Galaktionov O S,Peters G W M.Three-dimensional Mixing in Stokes Flow:the Partitioned Pipe Mixer Problem Revisited[J].European Journal of Mechanics-B/fluids,1999，18(5)：783-792.

[3] Kusch H A,Ottino J M.Experiments on Mixing in Continuous Chaotic Flows[J].Journal of Fluid Mechanics,1992,236：319-348.

[4] Mizuno Y,Funakoshi M.Chaotic Mixing Causedby Anaxially Periodic Steady Flowina Partitioned-pipe Mixer[J].Fluid Dynamics Research,2004，35(3)：205-227.

[5] Mizuno Y,Funakoshi M.Reynolds Number Dependences of Velocity Field and Fluid Mixing in Partitioned-pipe Mixer[J].Journal of the Physical Society of Japan，2005，74(5)：1479-1489.

[6] 王宗勇，陈超.多流道螺旋静态混合器混合性能的数值模拟[J].中国机械工程，2013，24(2)：268-279.

[7] 龚斌，包忠平，黄娜，等.元件长径比对SK型静态混合器湍流流场的影响[J].石油化工高等学校学报，2009，22(1):65-68.

[8] 李雅侠，华博，吴剑华，等.釜内螺旋半圆管夹套内流体湍流流动特性[J].过程工程学报，2011，11(6)：913-918.

[9] 李雅侠，吴剑华，龚斌，等.螺旋半圆夹套内湍流流动与传热的数值模拟[J].过程工程学报，2010，10(4)：644-649.

[10]李雅侠，王航，吴剑华.螺旋半圆管夹套内充分发展层流流动与换热特性[J].化工学报，2010，61(11)：2796-2803.

[11]李雅侠，王航，吴剑华，等.螺旋半圆管夹套内层流流动及换热特性研究[J].化学工程，38(6)：35-38.

[12]刘雯，骆政园，白博峰.管内含螺旋纽带诱导的螺旋涡特性[J].化工学报，2011，62(11)：3115-3122.

[13]Moffatt H K.Viscous and Resistive Eddies Near a Sharp Corner[J].Journal of Fluid Mechanics，1964，18(1)：1-18.

[14]Liu C H，Joseph D D.Stokes Flow in Wedge-shaped Trenches[J].Journal of Fluid Mechanics，1977，80(3)：443-463.

[15]Hills C P.Eddy Structures Induced Within a Wedge by a Honing Circular Arc[J].Theoretical and Computational Fluid Dynamics，2001，15(1)：1-10.

[16]Krasnopolskaya T S.Two-dimensional Stokes Flow Near a Corner in a Right Angle Wedge and Moffatt’s Eddies[J].Mechanics Research Communications，1995，22(1)：9-14.

[17]Krasnopolskaya T S,Meleshko V V,Peters G W M,et al.Mixing in Stokes Flow in an Annular Wedge Cavity[J].European Journal of Mechanics-B/fluids,1999,18(5):793-822.

[18]Galaktionov O S，Meleshko V V，Peters G W M.Stokes Flow in a Rectangular Cavity with a Cylinder[J].Fluid Dynamics Research，2005，24(2)：81-102.

Numerical Simulation of Stokes Flow Characteristics in the Fan-shaped Duct

WANG Zong-yong, ZHAO Jia-yu, WU Jian-hua, WANG Shu-ting

(Shenyang University of Chemical Technology， Shenyang 110142， China)

The flow characteristics of the fan-shaped duct with rotating circular wall at low Reynolds number is simulated,and the patterns of the velocity,vorticity and stream function are obtained at various sector angles.The results show that the 3D Stokes flow at low Reynolds number within the sector duct can be decomposed into two 2D flows,namely the axial flow in the straight duct driven by pressure drop and the sectional flow in the fan-shaped cavity induced by circular lid rotation.Axial velocity and circumferential velocity within the duct is symmetrical about sector bisector,while radial velocity is anti-symmetrical.With the decrease of sector angle,more and more vortex regions emerge in the sector duct,and the velocity field,vorticity field or stream function in the vortex regions isself-similar to each other,which shows that the fluid flow in the fan-shaped duct withrotating outer wall is of chaotic characteristics.Under the same Reynolds number,vorticity in the duct rises with the decrease of the sector angle,which implies that the small angle fan-shaped channel is good for fluid mixing.

Stokes flow； helical flow； low Reynolds number； velocity field； vorticity field

2013-12-02

辽宁省百千万人才工程项目(2013921047)；辽宁省高校优秀人才支持计划项目(LJQ2012036)

王宗勇(1973-)，男，辽宁辽阳人，副教授，博士，主要从事化工过程强化、非线性转子动力学等方面的研究.

2095-2198(2015)01-0037-06

10.3969/j.issn.2095-2198.2015.01.009

TQ051.7

A