某矿无底柱分段崩落法结构参数研究
2015-03-22何文俊
何文俊
(金诚信矿业管理股份有限公司,甘肃酒泉 736101)
采矿方法结构参数不仅直接影响到开拓、采准以及回采的工程量,而且还影响到投资、成本和矿山企业的效益等[1]。合理的采场结构参数是获得较好的开采效果的前提和基础。尤其针对采用崩落法的矿山,其损失贫化的管理意义更加重要[2,3]。
某铁矿位于云南省玉溪市,是目前国内最大规模的地下冶金矿山之一,地下开采一期设计年产能力为400万t/a,设计采用高分段、大间距无底柱分段崩落采矿法及先进的无轨采掘及装运设备,一期正在采用的分段高为20 m,进路间距20 m。为保证一、二期生产的正常衔接及更大参数回采的需要,二期规划拟在400 m以下两个水平将分段高度提高到30 m。因此,为满足矿山生产能力的需要,有必要对矿山现有采矿方法的崩矿步距、进路间距等结构参数进行相关研究。
目前,针对进路间距等相关参数的研究,主要集中在模拟试验、现场典型采场试验、软件模拟等手段[4],考虑到现场典型采场试验的耗时耗力等缺点,本文将模型试验与软件模拟相结合的方法,首先用相似模拟试验进行崩矿步距的确定,在确定好崩落步距之后,再在已有的崩矿步距情况下,进行分段高度及进路间距参数的优化。
1 崩矿步距优化
崩矿步距的确定主要通过实验室相似模拟试验手段模拟采矿现场放矿,在满足几何相似与力学相似的前提下,建立相似模型,从而使得模型放矿过程与现场放矿过程达到相似物理模型的实验室试验。
根据矿山现有的采矿方法,采用高分段(分段高度为30 m)端部放矿,本次采用立体模型试验。通过立体试验对不同放矿步距下的回采率及贫化率等指标进行分析,得到高分段下最优放矿步距、崩矿步距及进路口参数。试验模型按与现场比例1∶100制作,模型为木质框架结构,巷道呈菱形交错布置,共布置5个分层,每个分层3到4个进路,进路间距为0.2 m,每个进路布置四个步距,各步距均采用可抽出式铁皮制作,模型正面如图1所示。

图1 模型正面图
为了与该高分段放矿形式相适应,减少损失贫化,提高生产能力和回收率,进路间距取20 m。立体试验在此分段高度及进路间距条件下,选择合适的放矿步距及进路参数组合,放矿步距拟分别取5.04 cm、6.16 cm、6.72 cm、7.56 cm,进路宽度拟取4.2 cm×4 cm和4.9 cm×4 cm两种。选择放矿椭球体完整的进路口放出数据进行分析研究,计算各分段及所有分段的放出矿岩总量、放出矿石量、放出岩石量,并计算矿石的回收率、废石混入率及相应的回贫差等值,结果见表1。
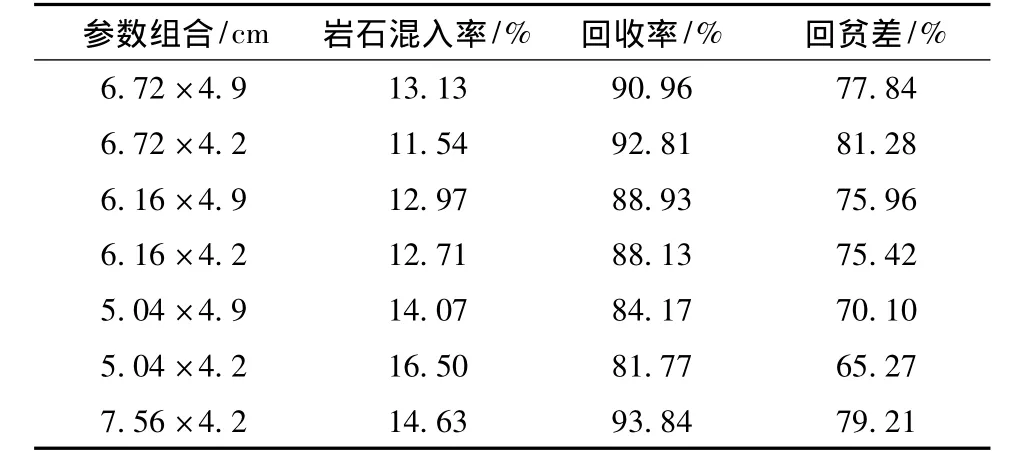
表1 立体试验结果汇总表
综合分析各立体试验模型的回收率、贫化率和废石混入率指标,当进路间距为20 m时,在所有的立体试验模型中,放矿步距为6.72 cm,进路尺寸宽4.2 cm高4 cm时回贫指标最优,此时的回收率为92.81%,废石混入率为11.54%,回贫差为81.28%。本次试验合理放矿步距应在6.72~7.56 cm。
依据其他矿山经验,一般实验室的放矿步距是现场崩矿步距的1.2~1.4倍,根据实践经验,矿山选择的段高和进路间距都比较大,因此选取K=1.4进行修正,由此求的本矿现场的合理崩矿步距应为4.8~5.4 m。
2 进路间距的优化
进路间距的确定主要通过PFC3D软件进行相关模拟确定。PFC3D可模拟任意大小球形颗粒的集合体的动力学行为,可以自动生成统计学上特定分布形式的颗粒集合,颗粒的半径可以均匀分布(即颗粒半径都相等)[5,6]。
为了与该高分段放矿形式相适应,减少损失贫化,提高生产能力和回收率,需确定最佳采场结构参数组合,进行进路间距优选,拟分别选取进路间距20 m、25 m进行试验比较,以确定最佳进路间距。本次实验分别建立30 cm×20 cm与30 cm×25 cm两种参数组合放矿模型,分别进行数值模拟得到各自不同的回贫指标,以比较这两种参数组合的优劣。
利用PFC3D内“墙”功能生成各边界,BALL功能生成大小不等的球来模拟矿石与废石,其中灰色(颜色较黑)颗粒代表废石,白色颗粒(颜色较淡)代表矿石。如图2所示。
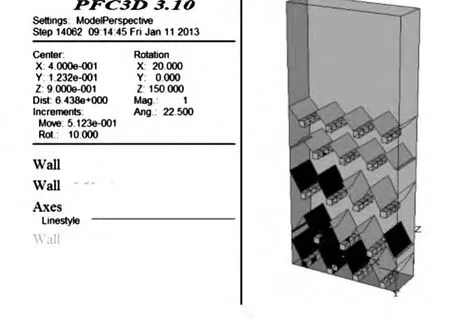
图2 PFC3D放矿模型结构侧视图
从图2可以看出,放矿颗粒受周围墙体的约束,随着放矿的进行,通过按照一定规律解除墙体对颗粒的约束,从而达到放矿模拟的目的。
为与实验室物理模型的相同,数值模型所设定放矿顺序与其一致,即高度上从上到下,各分段内依次从一端向另一端推进,各放矿口严格按照设定好的截止品位出矿,同一进路口由里向外分步距放矿,如图3为分段放矿模拟的过程图,从图3中可以看出模拟矿石及废石矿岩接触面下落形态呈漏斗状下落,这与现场较为吻合。

图3 PFC3D放矿过程(第五分段)
根据放矿口放出的矿石及废石的质量数据进行回采率与贫化率的计算与统计,模拟试验结果见表2。
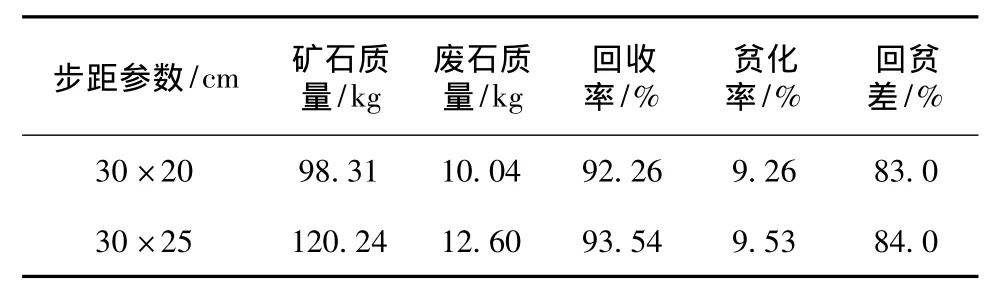
表2 软件模拟试验结果
通过该数值模拟结果分析可以看出在高变分段情况下,30 cm×25 cm参数组合模型的回贫差要高于30 cm×20 cm参数组合模型,从模拟结果可以得知,高变分段参数组合30 m条件下,进路为25 m时可以取得较优的指标。
3 小结
1.以某铁矿放矿生产实践为背景,将实验室相似模拟试验与PFC3D软件数值模拟相结合,得到了放矿步距及进路尺寸参数组合、进路间距值等参数,对矿山放矿工作具有重要意义。
2.通过实验室相似模拟立体放矿试验得到了该铁矿高变分段下合理放矿步距指标为6.72~7.56 m,合理的崩矿步距为4.8~5.4 m。
3.通过PFC3D建立数值放矿模型,实现了放矿全过程的动态再现,得到了无底柱分段崩落法放矿不同结构参数组合下的损失贫化指标,从而优选出合理进路间距指标为25 m。
[1] 解世俊.金属矿床地下开采[M].北京:冶金工业出版社,2006.
[2] 刘兴国,周骥.放矿理论基础[M].北京:冶金工业出版社,1995.
[3] 王昌汉.放矿学[M].北京:冶金工业出版社,1982.
[4] 刘振东.无底柱分段崩落法结构参数优化研究[D].衡阳:南华大学,2011.
[5] 钱志军,徐长佑.自然崩落法矿体崩落过程的数值模拟[J].化工矿山技术,1993,22(1):21 -24.
[6] 王连庆,高谦,王建国,等.自然崩落采矿法的颗粒流数值模拟[J]. 北京科技大学学报,2007,29(6):557 -561.
