一种U 形阻尼器力学性能分析

徐增武 杨应华

(1．长沙有色冶金设计研究院，长沙410011;2．西安建筑科技大学土木工程学院，西安710055)

1 引言

自1972年Kelly等［1］首次提出利用金属耗能减少结构的地震反应以来，金属耗能减震技术的研究与应用日趋成熟。金属耗能器是利用金属进入塑性状态后具有良好的滞回特性并在塑性滞回变形过程中吸收大量能量的原理制造出来的。国内外学者对金属耗能器进行了大量的研究，开发出众多阻尼器，主要为三大类:钢耗能器、铅耗能器和形状记忆合金耗能器。其中，钢耗能器具有形状设计自由、加工容易、维护成本低等优点，因此诸多学者对其深入研究并开发出各式阻尼器。从钢阻尼器耗能时主要受力状态可将其划分为四类:

(1)扭转型:Kelly 和 Skinner［2］研究的扭转梁属于扭转型，由于产生较大的扭转变形需要的尺寸过大，经济性差，此类产品较少。

(2)剪切型:Seki等［3］研究的剪切钢板耗能器属于剪切型，Yasumasa等［3］对剪切钢板耗能器进行了反复加载试验研究，试验结果表明:在循环荷载作用下，滞回特性很稳定，且具有较高的阻尼比。

(3)拉压型:Wakabayashi［4］在 1973 年研制的约束钢构件耗能器属于拉压型，Wakabayashi对该型阻尼器进行了拉压试验，试验结果同样表明，它具有较强的耗能能力、滞回曲线饱满，并对不同的无黏结材料进行了对比分析。

(4)弯曲型，弯曲型的钢耗能器则较多，如Marioni［5］研制的变高度圆形钢耗能器，邢书涛与郭迅［6］提出的中空菱形矩形板钢耗能器。其中Marioni对其研制的耗能器进行了大量研究研究，试验结果表明:变高度圆形钢耗能器具有较高的屈服率、同时阻尼特性稳定，该阻尼器已在实际桥梁工程上运用［7］。

通过对国内外钢耗能器的综述，并根据耗能器受力特性进行分类，得出弯曲型钢耗能器的滞回特性最为稳定，滞回变形能力最强，也是已研究成果中最多的一种，且众多成果已在实际工程上应用。

本文作者提出了一种带U形阻尼器梁柱节点［8］，U 形阻尼器弯曲型钢耗能器。文献［9］给出了U形阻尼器抗侧刚度及极限荷载的计算公式，不过其给出的计算公式的精度较差，本文重新对U形阻尼器的弹性刚度以及极限荷载进行了理论分析并提出了精度更高的计算公式，并进行了有限元验证。

2 U形阻尼器结构及力学模型

2．1 U形阻尼器构造

本文所提出的带U形阻尼器节点构造如图1所示，这种节点在拼接梁的腹板及下翼缘处均设置了U形阻尼器，这种节点主要通过U形阻尼器的塑性变形吸收能量，阻尼器越多面积进入塑性，耗能效率越高。U形阻尼器的构造特征如图2所示，阻尼器由U形段和平板段构成，阻尼器的平板段厚度要大于U形段的厚度，以保证阻尼器无论是在压力还是拉力的作用下，塑性铰均发生在阻尼器的U形截面段，平板段上开有螺栓孔，U形阻尼器力学性能主要由 c，d，t1，t2，R 控制。

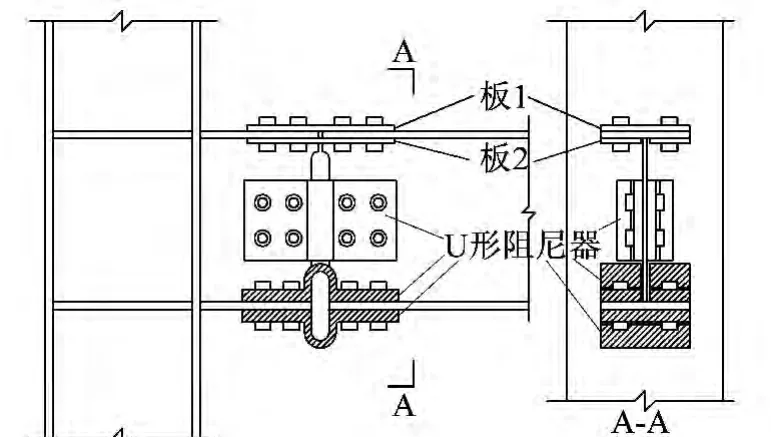
图1 带U形阻尼器钢框架节点Fig．1 Connection with U-shaped dampers of steel frame structure

图2 U形阻尼器Fig．2 U-shaped damper

2．2 U形阻尼器刚度

2．2．1 U形截面直段抗侧计算高度

文献［9］中计算U形阻尼器抗侧刚度时将阻尼器U形截面段与平板段的交接处视作刚域，但按这种假设计算出的阻尼器弹性刚度将会比实际大很多。本文对这种假设进行了修正，提出了更为合理的假设。对阻尼器进行抗侧刚度进行计算时，本文将平板段计算长度按图2中c值选取，并对阻尼器U形截面段直段的计算抗侧计算高度做了修正，通过大量有限元分析得出，当t2/t1≤0．85时，U形阻尼器U形截面段直段的计算高度可按下式进行计算:

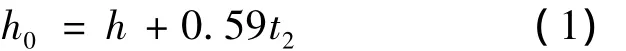
2．2．2 U形阻尼器抗拉刚度

当在拉力作用下时，U形阻尼器平板段末端的弯曲变形将会受到与平板段连接的构件的限制，故在计算U形阻尼器的抗拉刚度时可视作阻尼器平板段与U形段连接处有一竖向约束，阻尼器截面可用梁单元表示，结合2．2．1节的假设，U形阻尼器计算抗拉刚度时的力学模型可按图3所示的理想模型进行分析计算。

通过虚功原理可以计算出阻尼器在拉力P作用下弹性阶段的弯矩分布，如图4所示，图中m，n值可按以下两式计算得到:

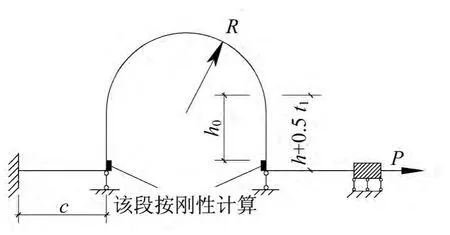
图3 拉力P作用下U形阻尼器分析模型Fig．3 Analysis model of U-shaped damper under tension force P

式中，E为U形阻尼器的弹性模量;Ir和Ij分别为U形阻尼器U形截面段及平板段相应的截面惯性矩。

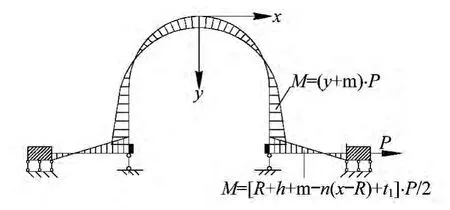
图4 拉力P作用下U形阻尼器弯矩图Fig．4 Bending moment diagram of U-shaped damper under tension force P

阻尼器的抗拉弹性刚度可根据阻尼器在拉力作用下的弯矩图计算得到:

式中，e=R+m。

2．2．3 U形阻尼器抗压刚度

当在压力作用下时，U形阻尼器平板段末端的弯曲变形将不再受到与平板段连接的构件的限制，故U形阻尼器计算抗压刚度时的力学模型可按图5所示的理想模型进行分析计算。

通过虚功原理可以计算出阻尼器在压力P'作用下弹性阶段的弯矩分布，如图6所示，图中s值可按下式计算得到:

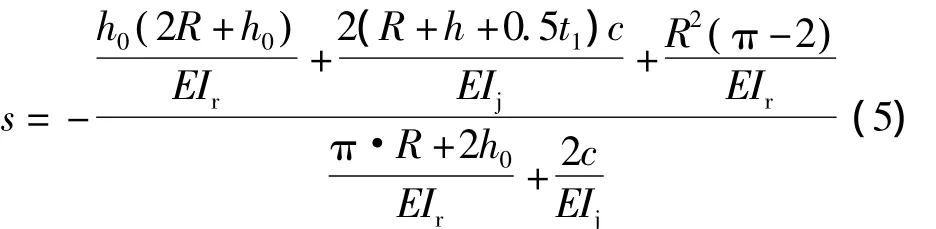
图5 压力P'作用下U形阻尼器分析模型Fig．5 Analysis model of U-shaped damper under pressure P'

阻尼器的抗压弹性刚度可根据阻尼器在压力作用下的弯矩图计算得到:

式中，f=R+s。

通过比较式(4)与式(6)可以看出，U形阻尼器的弹性抗拉刚度比弹性抗压刚度要大。

图6 压力P'作用下U形阻尼器弯矩图Fig．6 Bending moment diagram of U-shaped damper under pressure P'

2．3 U形阻尼器极限荷载

2．3．1 矩形截面全截面塑性弯矩

图7为一平板在全截面塑性弯矩Mu'作用下的受力分析图。以图7中的A—A截面为受力参考平面，在MuP'作用下A—A截面的中性轴(y=0)以上部分受压，中性轴以下部分受拉。受压部分将会在x轴方向发生膨胀，受拉部分将会在x轴方向产生收缩，由于平板受压部分和受拉部分是个整体，受压部分与受拉部分沿x轴方向的变形将会相互制约。受压单元沿着平板宽度方向的膨胀受到制约时，x轴方向必然要产生压应力才能限制其膨胀;同理要限制受拉单元沿着x轴方向的收缩变形，沿着板宽度方向必然要有与之相应的拉应力。

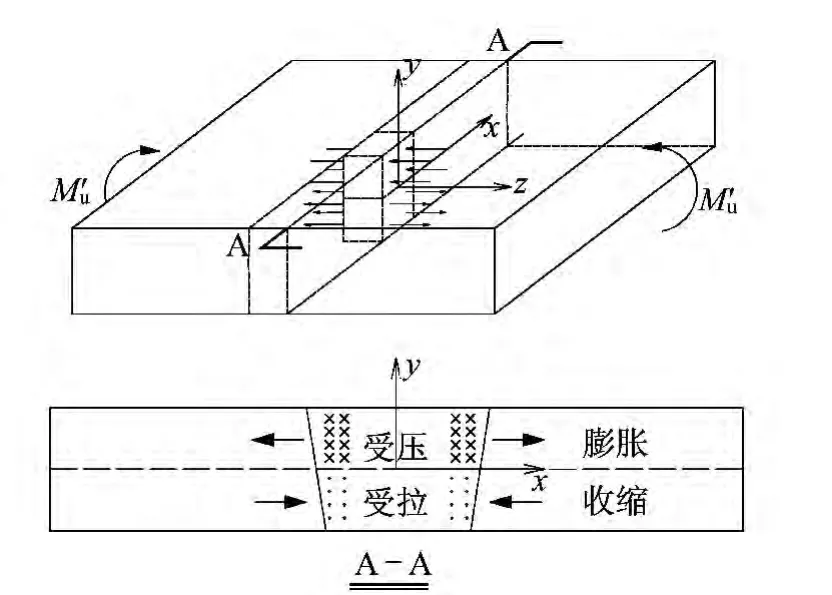
图7 平板受弯分析图Fig．7 Analysis diagram for plate bending

由于平板的厚度很小，厚度方向在弯矩作用下产生的应力可近似取为0。设A—A截面某一单元沿z轴方向的应力为σ，沿x轴方向的应力为ασ(α为板宽度方向应力系数，且0≤α≤1)，根据Von-Mises屈服准则可得:

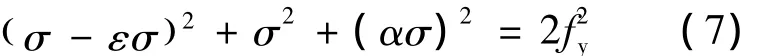
即

式中，fy为钢材的屈服强度，由于0≤α≤1，因此可以通过式(8)得出:

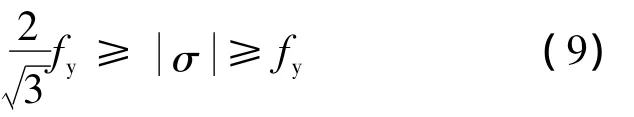
由式(9)可知:

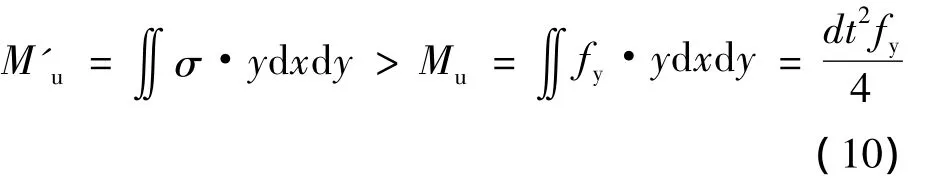
式中，Mu为矩形截面不考虑x轴方向应力影响时的全截面塑性弯矩;d为矩形截面的宽度;t为矩形截面厚度。

通过有限分析整理出矩形截面的全截面塑性弯矩可按下式计算:

式中，β为矩形截面塑性弯矩提高系数，可按表1取值，由表1可知，矩形截面宽厚比越大，β值越大，β 值均不超过1．15。

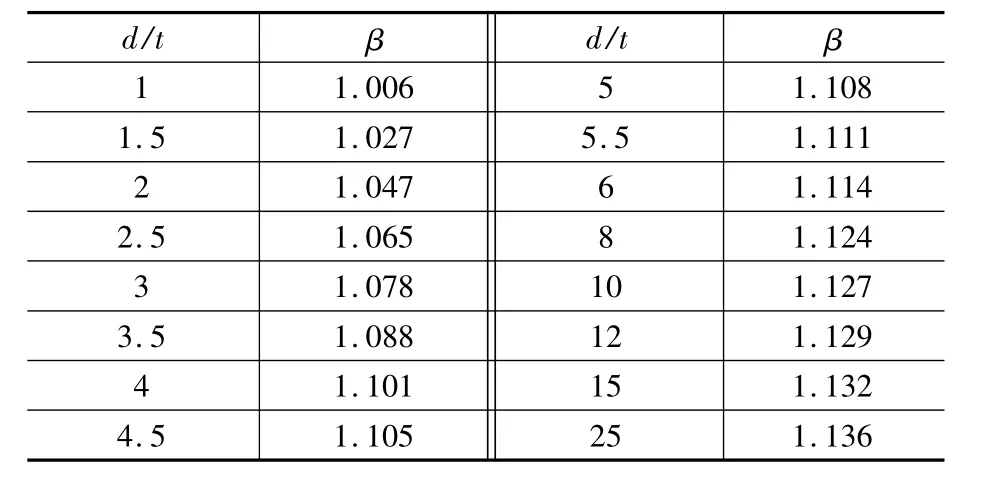
表1 矩形截面塑性弯矩提高系数Table 1 Enlarged coefficient of plastic moment for rectangular section

2．3．2 U形阻尼器塑性铰发生位置

在极限荷载状态下，大的塑性变形只发生在阻尼器U形截面段，因为这部分由相对较小的厚度。理想情况下的U形阻尼器在极限荷载作用下的塑性铰发生的位置如图8所示，一个塑性铰发生在U形段顶部，两个塑性铰发生在U形截面段的底部。而实际上由于U形阻尼器U形段底部受到平板段的限制，阻尼器的塑性铰将不会发生在U形段底部，而是会发生在距离底部微小距离处，图9为U形阻尼器在拉力作用下U形阻尼器y向主应力云图，由图9可以看出，阻尼器的塑性铰发生在距U形截面段底部偏上处。通过大量有限元分析得出，当(R+h)/t2＞1．6时，阻尼器将在U形截面段顶部以及距离U形截面段底部0．14t2处产生塑性铰。

图8 理想状态下U形阻尼器塑性铰发生位置Fig．8 Plastic hinge location of U-shaped damper in ideal status

图9 极限荷载作用下阻尼器y向主应力云图Fig．9 y-axis principal stress contour of damper under ultimate load

2．3．3 U形阻尼器极限荷载计算

计算极限荷载时可认为阻尼器U形截面段与平板段交汇处为刚性，结合2．3．2节中对阻尼器塑性铰发生位置的分析，U形阻尼器可按图10所示U形阻尼器极限荷载计算简图进行极限荷载计算。

图10 U形阻尼器极限荷载计算简图Fig．10 Ultimate load calculation diagram of U-shaped damper

图10 中，M'u和θp分别表示极限状态下的塑性弯矩和塑性转角;z=R+h－0．14t2。根据能量守恒定律可以计算得阻尼器的极限荷载计算公式为:

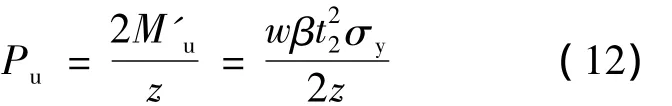
3 有限元验证

3．1 阻尼器分析模型

本文通过有限元软件Abaqus对U形阻尼器进行力学性能分析，其分析模型如图11所示，两个U形阻尼器与两块钢板通过高强螺栓相连，其中一块钢板侧边完全固定住，另外一块钢板侧边约束了图中y轴与x轴方向的自由度，z轴方向自由以便施加水平荷载。钢板一自由端平面与其平面外一点耦合，并将水平荷载施加在该耦合控制点上。两块钢板的规格均为－200×200×16，阻尼器及钢板均采用 Q235钢，采用10．9级M22的高强螺栓进行连接，这种规格的螺栓预紧力能达到190 kN［10］。本文分了四组共9个不同规格的U形阻尼器进行有限元分析，各阻尼器的截面规格如表2所示，阻尼器的宽度均为200 mm，其中U1为基础模型，第一组模型主要通过改变阻尼器U形段厚度t2进行分析，第二组模型通过改变阻尼器U形段直段高度进行分析，第三组模型通过改变阻尼器的U形段半径进行分析，第四组模型则通过改变阻尼器平板段厚度进行分析。

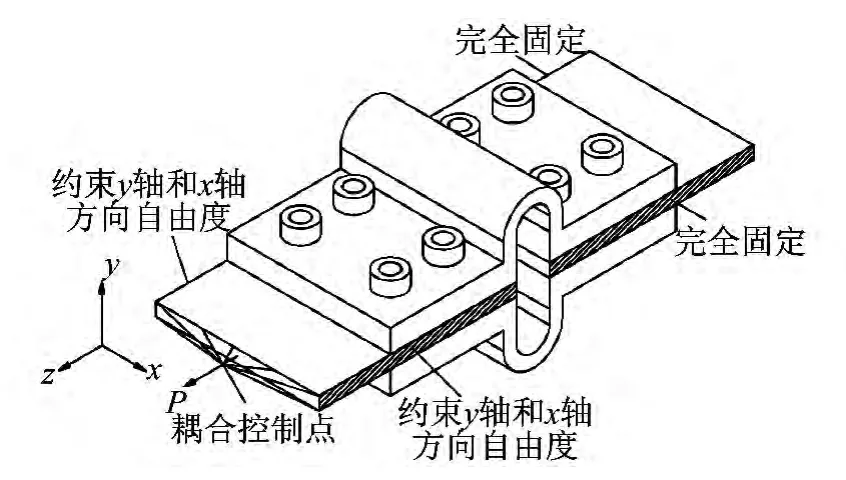
图11 U形阻尼器模型三维图Fig．11 Three-dimensional figure of U-shaped damper

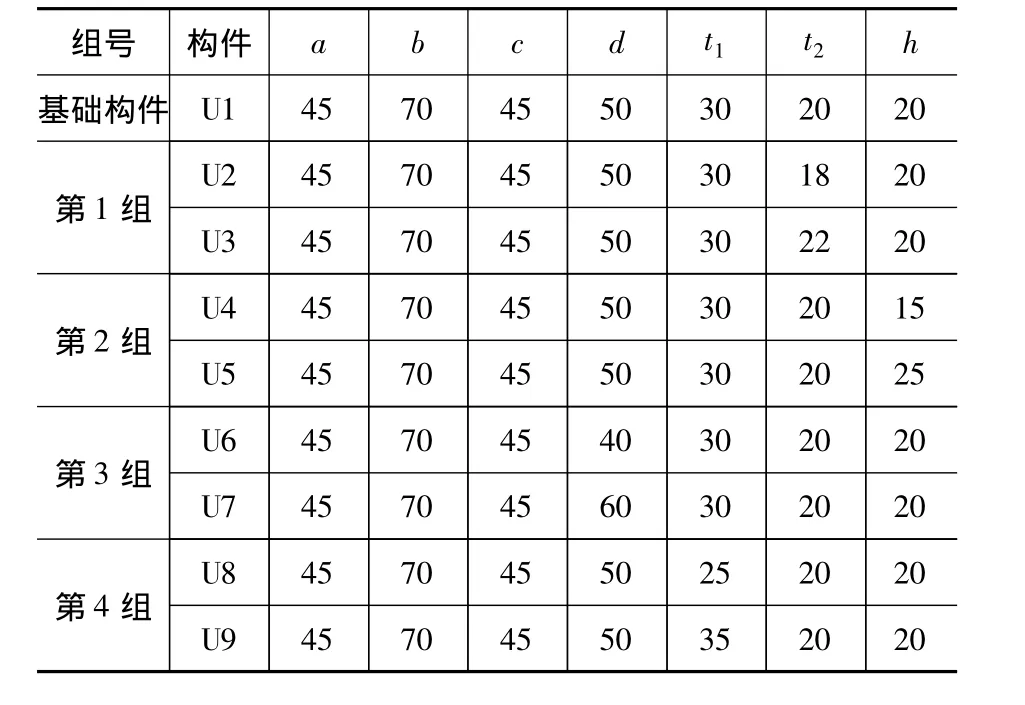
表2 U形阻尼器模型参数Table 2 Parameters of U-shaped damper model

各阻尼器模型均采用实体单元建模，选择的单元类型为8节点六面体线性减缩积分单(C3D8R)，该单元适合弹塑性分析和接触分析，对模型进行网格划分时，根据应力梯度划分不同密度的网格，在应力梯度较大处采用较大的网格密度，U形阻尼器的网格划分如图12所示。

图12 U形阻尼器网格划分Fig．12 FE mesh of U-shaped damper

本文基于理想弹塑性模型对U形阻尼器力学性能理论分析，因此有限元分析时钢材的本构模型也采用理想弹性塑性模型，模拟的钢材本构参数详见表3。

有限元模型考虑螺栓杆与螺栓孔壁之间的接触关系，接触属性中的法向作用采用默认的“硬接触”，并假设螺杆与孔壁之间无摩擦。为了简化计算，螺帽通过绑定的形式与各连接件相连接。钢板与U形阻尼器间的接触对的法向用作同样采用默认的“硬接触”，而切向设有抗滑移系数，其取值为 0．45［10］。

本文采用单调加载的方式对U形阻尼器的力学性能进行分析，由于阻尼器在拉力和压力的作用下力学性能有差异，因此对阻尼器在拉力方向上和压力方向上均做一次单调加载，并以拉力方向为正，压力方向为负。

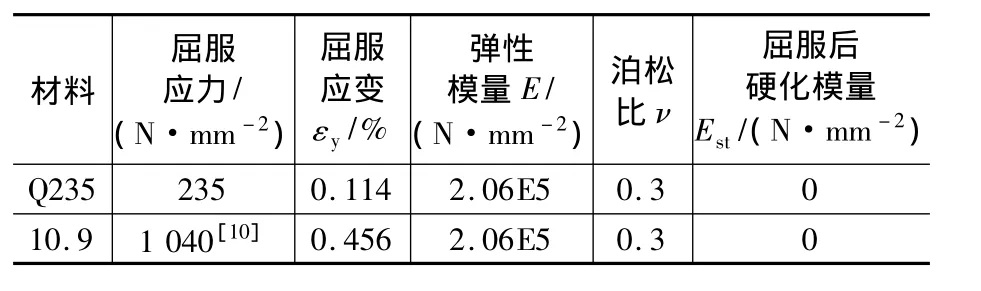
表3 钢材本构关系Table 3 Constitutive relation for steel

3．2 Abaqus有效性验证

通过ABAQUS模拟文献［9］中的SP1—SP4试件。试件几何尺寸、材料属性、边界条件及荷载条件均按照文献［9］中进行，将模拟得出的带U形阻尼器的梁柱弱轴连接节点的滞回曲线与文献中的滞回曲线进行对比(图13)。由图13(a)可以看出，有限元计算结果和试验结果吻合较好，有限元模拟得出的滞回曲线与试验得出的滞回曲线趋势相同。从图13(b)中可以看出，SP1—SP4的有限元模拟的骨架曲线和试验骨架曲线的偏差均很小，其中在SP2在加载位移为0．013 rad时的偏差最大，其有限元模拟对应的荷载为199．8 kN，而实验对应的荷载为212．3 kN，试验值对应于有限元模拟值要大6．3%。因此，前述Abaqus有限元模型具有较高的精度，可用于后文模型试件的分析。

3．3 有限元分析结果

图14为U形阻尼器通过有限元分析得出的荷载位移曲线及理论公式计算得出荷载位移曲线的比较，从图中可以看出数值曲线和理论曲线吻合度很高，两曲线的初始刚度和屈服荷载均比较接近。

表4列出了各U形阻尼器分别在拉力及压力作用下的初始刚度解析解与数值解，并对初始刚度的数值解与解析解进行了比较。从表4可以看出，初始刚度的数值解与解析解之间的偏差都在5%以内，吻合得很好，因此使用式(4)及式(6)对U形阻尼器的初始刚度进行计算有较高精度。

图13 有限元模拟曲线与试验曲线对比Fig．13 Comparison between test results and finite element simulation results

表5列出了各阻尼器的屈服荷载的数值解与解析解，并列出了两者之间的偏差。从表5中可以看出，屈服荷载的数值解与解析解之间的偏差均在5%以内，吻合度较高，因此使用式(12)对U形阻尼器的极限荷载进行计算也有较高精度。

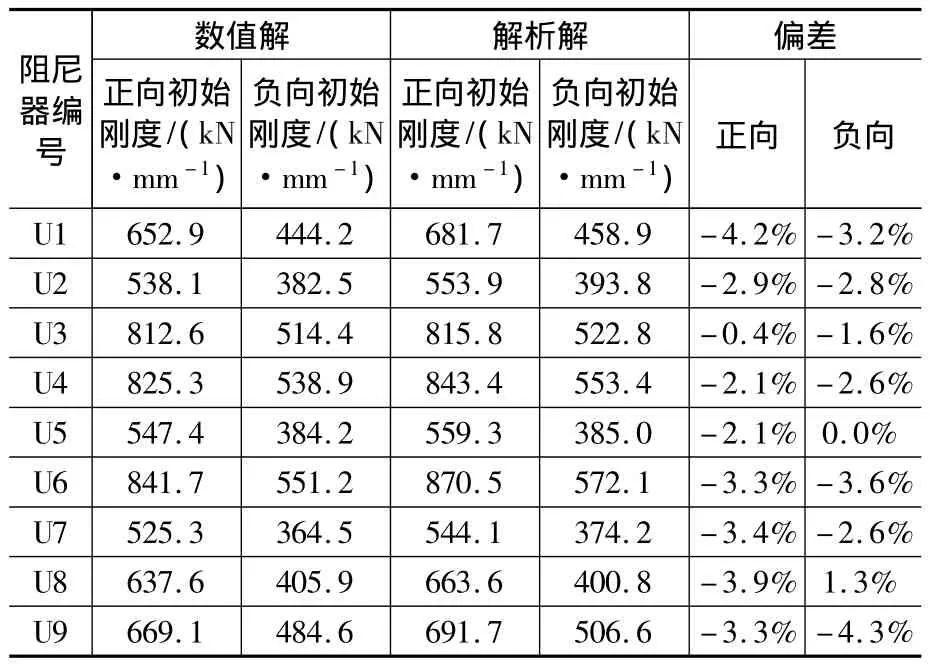
表4 初始刚度数值解与解析解对比Table 4 Comparison of numerical simulation results and analytical solutions for initial stiffness

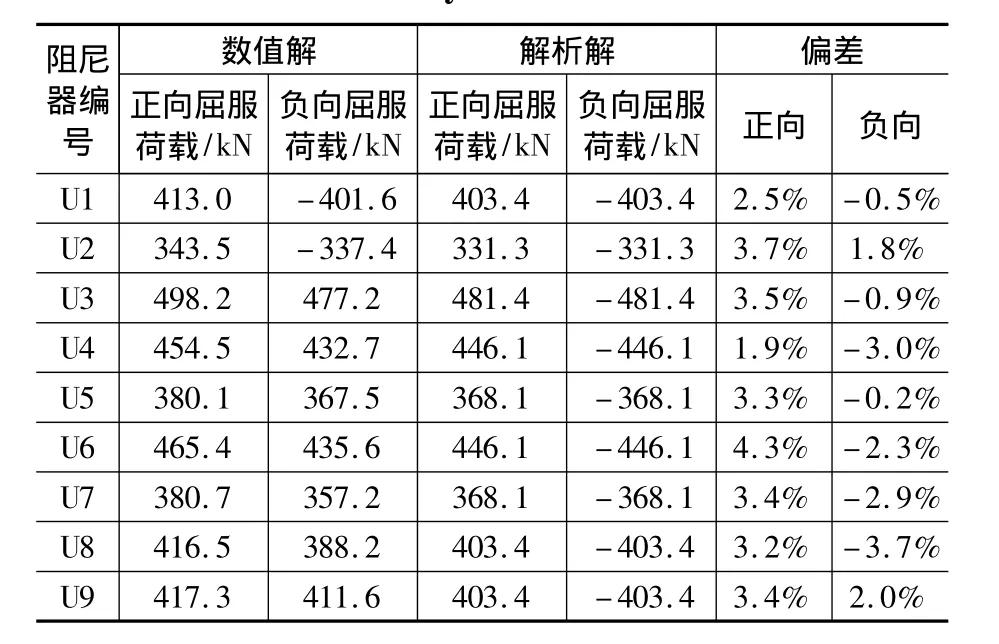
表5 屈服荷载数值解与解析解对比Table 5 Comparison of numerical simulation results and analytical solutions for yield load

4 结论

本文对U形阻尼器进行了理论分析、有限元仿真分析，得到如下结论:

(1)U形阻尼器的弹性抗拉刚度比弹性抗压刚度要大;

(2)矩形截面宽厚比的增加可以提高矩形截面的全截面塑性弯矩;

(3)U形阻尼器的塑性铰发生在U形截面段顶部及U形截面段底部偏上位置;

(4)有限元分析的荷载位移曲线与按理论公式计算得出的荷载位移曲线有较高的吻合度，说明本文理论分析公式可以应用于U形阻尼器设计。

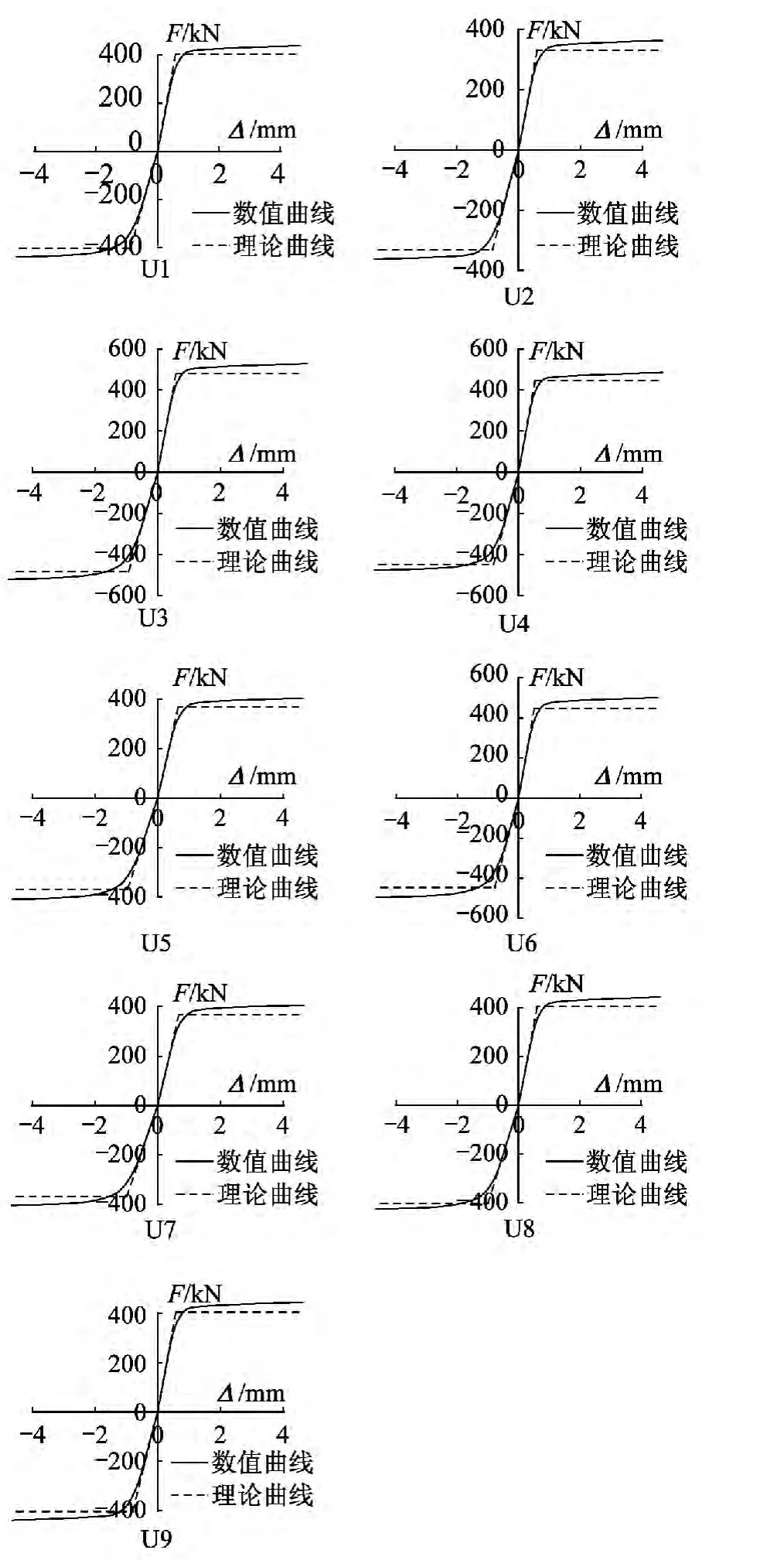
图14 U形阻尼器荷载位移曲线Fig．14 Load-displacement curve of U-shaped damper

［1］ Kelly J M，Skinner R I，Heine A J．Mechanisms of Energy absorption in special devices for use in earthquake resistant structures［J］．Bulletin of New Zeatomd．Society for Earthquake Engineering，1972，5(3):63-88．

［2］ Skinner R，Kelly J，Heine A．Hysteretic dampers for earthquake-resistant［J］．Earthquake．Engineering and Structural Dynamics，1975，3:287-296．

［3］ 周云．金属耗能减震结构设计［M］．武汉:武汉理工大学出版社，2006．Zhou Yun．Desgn of steel damped structme［M］．Wuhai:Wahan University of Technology Press，2006．(in Chinese)

［4］ 刘建彬．防屈曲支撑及防屈曲支撑钢架设计理论研究［D］．北京:清华大学，2005．Liu Jianbin．Research on the design theory of bucklingrestrained braces and buckling-restained braced frames［D］．Beijing:Tsinghua University，2005．(in Chinese)

［5］ 邢书涛，郭迅．一种新型软钢阻尼器力学性能和减震效果的研究［J］．地震工程与工程振动，2003，23(6):179-186．Xing Shutao，Guo Xun．Study on mechanical behavior and effectiveness of a new type of mild steel damper［J］．Earthquake Engineering and Engineering Vibration，2003，23(6):179-186．(in Chinese)

［6］ Marioni A．Development of a new type of hysteretic damper for the seismic protection of bridges［C］．Proceedings of the 4th World Congress on Joint Sealing and Bearing Systems for Concrete Structures，American Concrete Institute，1997:955-976．

［7］ Roussis P C，Constantinou M C，Erdik M，et al．Assessment of performance of seismic isolation system of Bolu viaduct［J］．Journal of Bridge Engineering，2003，8(4):182-190．

［8］ 杨应华，徐增武．一种带U形耗能元件的易修复梁柱节点，中国，ZL201320460254．2［P］．2013．Yang Yinghua，Xu Zengwu，An easily reparable beamto-column connection with U-shaped damper．Chinese Patent，ZL201320460254．2［P］．2013．(in Chinese)

［9］ Koetaka Y，Chusilp P，Zhang Z，et al．Mechanical property of beam-to-column moment connections with hysteretic dampers for column weak axis［J］．Engineering Structures，2005，27(1):109-117．

［10］ 陈绍蕃．钢结构［M］．2版．北京:中国建筑工业出版社，2009．Chen Shaofan．Steelstructure［M］．2nd Edition．Beijing:China Architecture and Building Press，2009．(in Chinese)