基于地域趋势收入模型分析的农村居民收入指数保险产品构建研究

2015-03-21王静媛陈盛伟

山东农业大学学报（社会科学版） 2015年1期

□王静媛陈盛伟

□王静媛陈盛伟

农村居民收入稳定对农村经济活动以及农业生产活动的发展具有重要作用。本文利用山东省农村居民2007-2011年收入数据序列，建立地域趋势收入模型，根据此模型对2012-2013年山东省农村居民收入进行预测。在此基础上进行农村居民收入指数保险的初步产品构建，并进行保险费用的厘定。农村居民收入指数保险能很好的稳定农户收入水平，可对涉农保险提供良好的技术支撑。

纯收入；指数保险；模型构建；费率厘定

一、引言

收入保险在国际上的应用起源于美国，是根据农民收入而非产量作为承保和赔偿的依据，是美国农业保险的一个创新，其主要的收入保险种类有团体收益保险(GRIP)、作物收益保险(CRC)、收益保证保险(RA)、收入保护保险(IP)、农场总收入保险(GFR)五种。由于我国农业保险起步较晚且农村金融市场发育不完善，上述依托在金融衍生工具上的收入保险在我国难以实行。我国目前关于涉农收入保险的研究主要针对农作物收入保险，如谢凤杰等(2012)以安徽省阜阳市为例，运用Copula方法估算玉米、小麦、大豆单产与价格的联合概率密度，测算了三种农产品的收入保险费率；肖宇谷等(2013)分析了中国开展农作物收入保险的意义，并对相应的价格指标选择进行了探讨。但关于收入保险的研究具有单一性和片面性，要想稳定我国农村居民的收入，需要在现有水平上不断创新农业收入保险产品种类，更好的改善农户的生产经营行为。

农村居民收入水平影响农民的生产行为和经济行为，特别是对于我国农村人口多、农户收入低、农业纯收入不稳定的现状来说，农村居民收入的稳定至关重要。本文试图利用地域趋势收入模型，以山东省为例分析农民的收入趋势，利用趋势收入与实际收入的差值作为收入损失，对山东省农民人均纯收入保险进行初步的研究和产品的构建，并建立收入指数模型。收入指数保险是根据农民历年纯收入序列，对未来农户的收入趋势进行预测，对农户低于预测收入的部分予以风险保障，即当收入低于某一触发值时，可实施相应赔付的一种新型指数保险产品。

二、农村居民收入指数保险的初步构建。

(一)趋势收入的预测

本文采用“地域收入模型”对山东省农户纯收入进行预测分析。可用等式表示为:Y=T×S×R。其中，趋势收入变动的历史数据(Y)，趋势收入变动因素(T)、地域变动因素(S)和随机因素(R)综合影响的结果(因多数地域不存在明显的周期波动因素，本文对它不作考虑)。用“地域收入模型”测定地域指数的思路是：第一步，求历年同地域的平均收入，消除部分随机因素(从理论上讲，在历史数据足够多的条件下，随机变量t的均值接近于零)。第二步，求出各地域的趋势值，并以此值去除历年同地域的平均值，便得出地域指数。本文以山东省17个地市农村居民2007年至2011年的农村居民纯收入为数据来源分析收入趋势。

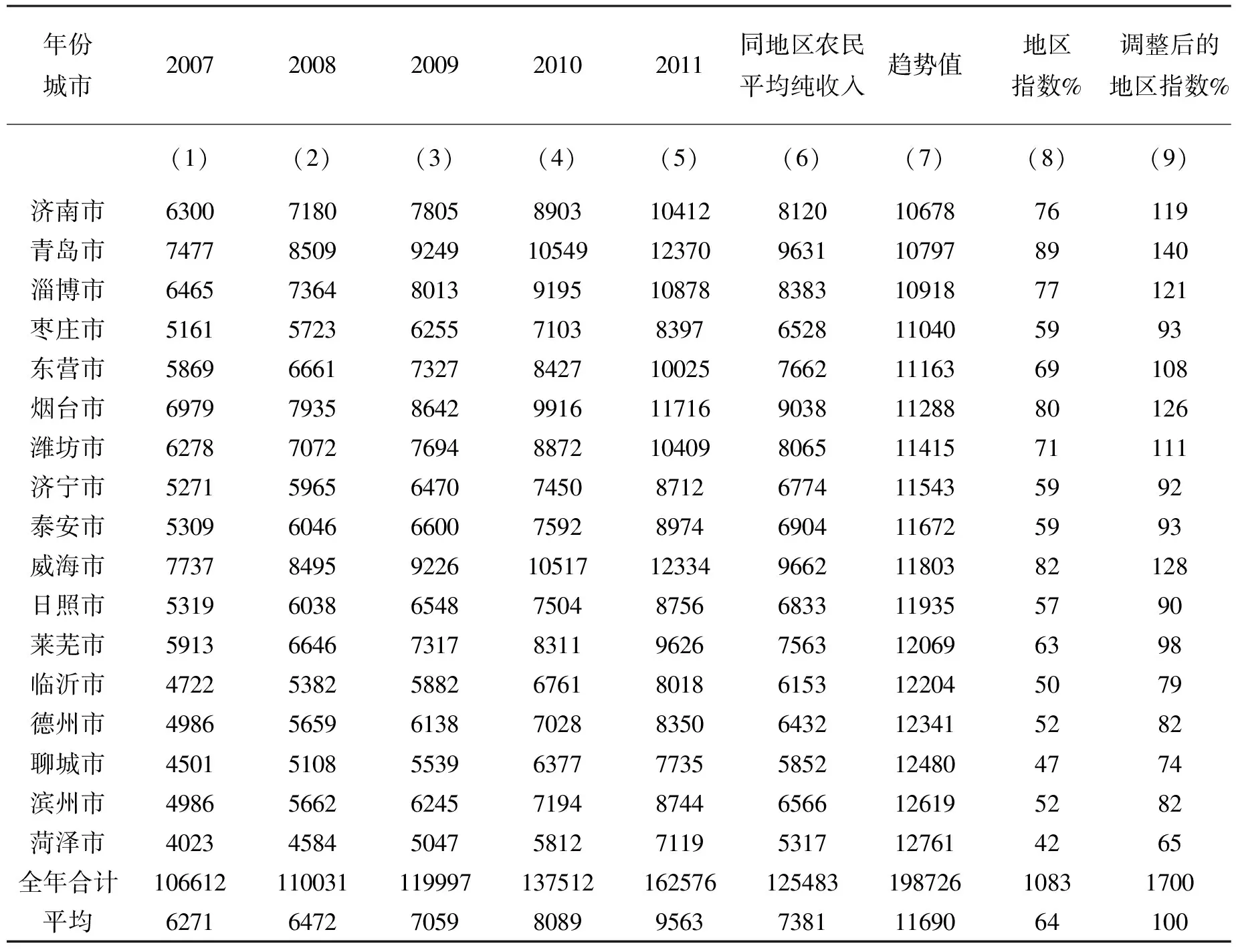
表1 山东省各市农村居民纯收入(2007-2011) 单位：元/人

第一步，计算同地区历年农民纯收入的平均值，列入表一第(6)栏。

第二步，趋势值计算，首先需要确定长期增长趋势特征，需要对表1中山东省五年的合计收入进行分析。通过直观分析可以看出，山东省农户的收入是递增的，数据是不平稳的，本文对收入数据进行单整分析，列出了收入数据的一阶和二阶单整序列(如表2)。

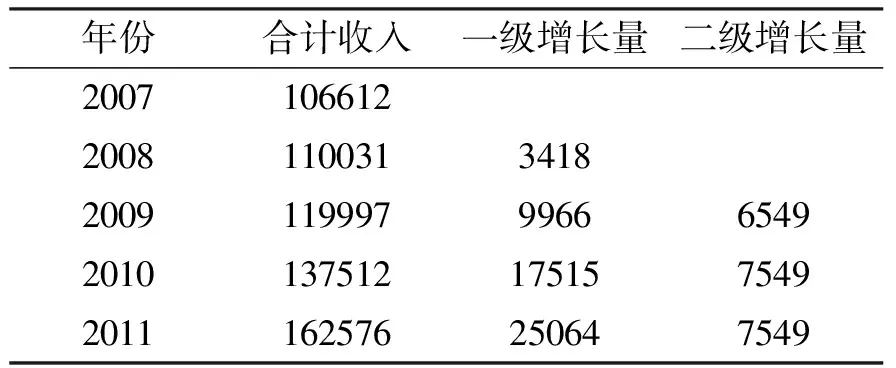
表2 历史数据特征分析表单位：元

由表2可以看出，山东省农村收入的二阶单整序列是平稳的，根据长期趋势模型特征，与历史数据特征的适应关系，需要选择二次模型进行分析，我们可利用表1中各地区平均数值与时间序列建立二次幂方程组，参数为a、b、c。另需选择中间点2009年为原点，即其时间值t为“0”。参数计算表的方式如下：

表3 参数计算表单位：百元

求得a、b、c分别为70.638，8.201，2.141，所以所求的二次方程为：

T=70.638+8.201t+2.141t2

(1)

(1)式是利用总收入趋势得到的17城市统一指标，研究需要具体到每一具体的地区，即认为每一地区的收入顺序是先后发生且存在区别的，因此，需要在T的基础上做出调整，调整公式如下：

(2)

进行了时间序列调整后的原点变为2009年的济南市，根据公式(2)式算出的趋势值列入表1中的列(7)，然后通过平均值除以趋势值得出区域指数，列为表1的(8)列，最终的指数总和为1083.2%。以调整系数(R=1700/1083.2=1.569)，分别乘以地区指数(8列)得到调整后的地区指数(9列)。最终的预测值为趋势值与地区指数的乘积。为了验证趋势收入模型的准确程度，我们根据各市的地域序列，通过趋势值算出2012年的最终预测值如下表所示。

表4 2012年山东省各城市的人均纯收入预测值单位：元/人

利用SPSS相关分析可知，山东省2012年和2013年农民收入的实际值与预测值的相关系数分别为0.868和0.905，均通过1%水平的显著性检验，该模型较好的拟合了山东省农民的收入趋势。

(二)农业收入指数保险产品的构建

1.农业收入指数保险的赔付设定

通过上述的分析，得出了农业人均纯收入趋势水平，通过趋势人均收入的计算，根据以上数据选取济南和泰安两市为例进行农民收入指数的初步构建。在确定了趋势产量的基础上，我们假定保险公司承保10%-30%的收入损失(可适当调整)，对农村居民收入能发生的损失进行担保，即担保标准为农村居民趋势收入70%-90%的损失部分。通过设定的保障水平，来求得特定收入保险保障水平下的收入保险指数，即10%的保险指数触发值和30%的保险指数最大赔付值，若收入低于平均收入的90%，启动指数赔付，若收入低于平均收入的70%，按照最大赔付额进行赔付，。如表五所示：

表5 收入保险指数赔付金额

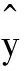
2.纯费率的厘定原理与方法

U=(1-p)U(m-π)+pU(m-π-d+I)

在假定保险公司交易成本为零的条件下，保险费率 π可以看作是保险合同 α与影响费率的其他风险特征 Z(如巨灾风险损失成本、信息成本等)的函数，即 π=π(α，z)。而赔付额 I也是保险合同 α的函数，即 I=I(α)。若有交易成本且参保农户的风险类型不可知，则保险市场供需均衡状态下的保险合同α由农户与保险公司视市场交易习惯而定(puelzandSnow，1994)。可见上式中的U因α的不同取值而不同。

当农户和保险公司达到期望效用最大时，根据本研究假设，需满足下列一阶条件:

I＇(α)和π＇(α,z)分别表示边际赔付和边际保费；p/(1-p)为有无产量损失的概率比，衡量购买该保险合同的相对风险。基于上述理论分析，在保险统计公平的费率下，如果农民购买了收入保险的全险，则农民在有无损失的情况下收到相同的收入，于是则有

U＇(m-π)=U＇[m-π-d+(α)]

由此可知，期望收益的边际效用比解释了为什么风险规避性农户更倾向于购买收入保险，同样的对于保险公司来说，则需要保险公司的期望收益等于其期望成本(之前的前提假定交易成本为零)，则有：

(1-p)π＇(α,z)=p{I＇(α)-π＇(α,z)}

于是：π＇(α,z)=p·I＇(α)

根据隐函数定理我们可以推断出，保险统计上公平合理的保费应该等于农户收入期望损失。

从而，得出合理的保险纯费率为

三、结语

本文利用地域趋势收入模型对山东省农村居民2007-2011年收入数据序列进行分析，得出农村居民收入的二级增长量数据相近，据此建立了趋势预测收入方程，并通过对地区指数调整，得到最终的区域趋势收入。然后对2012-2013年山东省农村居民的实际收入和预测收入进行相关性分析，结论认为，地域趋势收入模型能较好的预测地域收入水平。结合趋势收入的预测模型，本文创新性的提出了收入指数保险，在确定触发值以及风险等级损失概率的基础上，利用冯.诺伊曼——摩根斯坦效用函数对保险费率进行了厘定。

值得一提的是，本文采取的收入数据是以城市为单位的地区整体数据，然而收入保险的地域范围最多只能扩大到县域单位，因此，本文只提供一种理论上具有可行性的方法。

[1]周建涛，于然.我国农业保险应以农业经济作物收入保险为切入点[J].农业经济，2005，(1)：56-57.

[2]陈运来.发达国家农业保险模式变革的主要特征及启示[J].财经理论与实践，2008，(9)：34-38.

[3]度国柱.建设新农村需要加快农业保险建设[J].经济与管理研究，2006，(5):20-24.

[4]于洋，王尔大.基于保险精算原理的政策性作物保险定价研究[M].大连理工大学，博士学位论文，2010.

[5]谢凤杰. 基于Copula方法的作物收入保险定价研究——以安徽省阜阳市为例[J]. 农业技术经济，2011，(04)：41-49.

[6]周建涛，于然.我国农业保险应以经济作物收入保险为切入点[J].农业经济， 2005，(1)：56-57.

[7]孙良媛.论市场经济条件下的农业风险[J].广东社会科学, 2001，(3): 32-37.

[8]刘晶，葛颜祥，王爱丽.我国农产品价格风险及其防范研究[J].农业现代化研究, 2004，(6): 438-441.

[9]马九杰,崔卫杰,朱信凯.农业自然灾害风险对粮食综合生产能力的影响分析[J].农业经济问题，2005，(4)：14-17.

[10]张雯丽，龙文军.蔬菜价格保险和生产保险的探索与思考[J].农业经济问题,2014，(1)：66-71.

2014-11-02