基于鲁棒性的外加航班机组配对研究

乐美龙， 邹凯中

(上海海事大学 物流研究中心， 上海 201306)



基于鲁棒性的外加航班机组配对研究

乐美龙， 邹凯中*

(上海海事大学 物流研究中心， 上海 201306)

为了提高中小型航空公司的服务水平，增强其应对外加航班的灵活性，文章针对外加航班机组配对问题设计了新型的机组配对方案.在基于传统的机组配对模型上，满足外加航班机组配对的要求下，提出具有鲁棒性的机组配对模型.之后通过算例分析，用CPLEX软件对所建立的模型进行求解，得出了模型下目标函数的最优解.最后通过不同结果的对比，显示了鲁棒性建模方法的好处并表明鲁棒性模型在以相对较小的成本增加而不干扰已有航班的情况下可以为恢复提供自然的选择，为中小型航空公司在处理外加航班问题上提供有意义的参考.

中小型航空公司； 外加航班； 机组配对； 鲁棒性

在航空公司运营中，机组成本是继燃油成本之后的第二大成本项目.然而，与燃油成本不同，机组费用的大部分是可以控制的，对此很多学者进行了研究.Marsten和Shepardson[1]建立了机组排班问题的集划分模型，并采用隐枚举和拉格朗日松弛算法对模型进行了求解.Lavoie等[2]在早期采用列生成算法对机组排班问题进行了有效求解.Beasley和Chu[3]为非单一费用的集合覆盖问题设计了基于启发式的遗传算法.李耀华和谭娜[4]在求解机组指派模型时采用自然数编码的改进遗传算法，通过仿真验证了模型和算法的可行性.肖真真[5]建立了任务均衡的机组人员指派问题模型，并采用改进的自适应遗传算法进行求解.鲁红珍[6]提出了多目标的机组配对模型，最后对机组资源利用率最大的模型求解，验证了模型的可行性.

由于航班在实际的运营中会受到各种干扰，给航空公司造成很大的经济损失.为减轻这种干扰造成的损失，近来，鲁棒性的研究备受关注.EhrgottandRyan[7]对没有足够时间来吸收延迟的衔接进行惩罚，求解了一个最小化总成本和总惩罚成本的多目标最优问题.ShebalovandKlabjan[8]定义了移动机组来作为取得鲁棒性的一种方式，既在运营过程中，机组之间的计划可以进行交换.牟德一和张婧[9]在确定性经典模型的基础上，提出了具有鲁棒性的机组配对问题的随机规划模型.牟德一和王志新[10]建立了基于机组延误概率最小的鲁棒性机组配对模型并用Matlab进行了求解，结果表明模型产生的机组配对在应对干扰时更具鲁棒性.Schaefer等[11]以最小化期望总成本为目标函数来解决机组配对问题.YenandBirge[12]考虑了不确定性条件下的机组配对问题，把机组配对问题描述为一个两阶段的随机规划问题且探讨了两个连续航班之间的衔接时间对解的鲁棒性的影响.

然而，目前绝大部分的文献集中在航空公司的大规模问题上[13-14]，忽视了中小型航空公司的需求，这些需求之一是对临时的外加航班的管理.外加航班出现的原因有很多，例如某旅游路线的游客大增或包机等.目前，这种干扰是通过在运行中应用恢复程序进行处理[15].本文研究的是在机组配对的生成阶段考虑这些航班的插入，力求所得配对更具鲁棒性，使得在实际运行中有更多的方案来应对这种干扰.

1 机组配对问题

一个机组配对是由在机场的衔接时间和在每一个工作日结束后的休息时间间隔开来的一系列航班.一个配对可能跨越几个工作日并且由一个单独的机组执飞.在机组配对问题中，目的是要从所有可行配对中选择一个子集来覆盖航班计划表中的每一个航班并且每一个航班仅能被覆盖一次，同时还要保持机组总成本最小.这个问题可以看作一个集划分问题，如下所示：

(1)

yp∈{0,1},p∈p*，

(2)

式中，F是所有航班的集合，p*是所有可行配对的集合，cp是配对p∈p*的成本，参数aip=1，如果配对p覆盖了航班i；否则，aip=0.决策变量yp=1，如果配对p是解的一部分，否则，yp=0.目标函数是最小化所选配对的总成本.等式约束(1)确保每个航班有且仅能被覆盖一次.

2 问题描述和解决方法

在生成机组配对时需要遵守一系列复杂的规则，本部分要用到的标号如下.

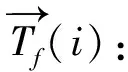
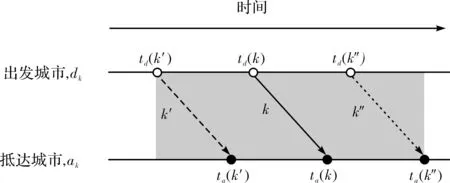
图1 外加航班k的时间窗Fig.1 The time window for the extra flight k

由于事先不知道可能的外加航班的准确时间，可以假设一个外加航班可能被插入的时间窗.通常，时间窗的信息可以由过去的经验或通过挖掘历史数据获得.图1是一个外加航班k的时间窗.在图中，横线表示起飞和抵达的城市，从左到右的箭头表示时间的推移.为了表示航班最早起飞和最晚抵达的时间，采用两个虚构的航班k′航班k″和表示.

为了覆盖外加航班，航空公司通常使用置位机组.然而，使用多于两个置位机组去覆盖一个外加航班是不可取的.因此，我们假设在一个方案中只允许不多于两个置位机组的情况出现.根据规定，花费在机组置位期间的时间会部分地算作勤务期内的飞行时间.允许机组置位时间th(i,j)与相应的实际飞行时间不同.而且，置位机组的最小等待和休息时间可以与机组执飞正常航班时的不同.

为了处理外加航班的问题，测试了至多带有两个机组置位的所有可能的恢复选择，解决方案可分为如下两种类型：

A类型：两个配对被选择以用于在运行过程中交换执行这些配对的机组来覆盖一个外加航班.

B类型：只有一个配对被选择，配对中两个连续的航班之间必须有足够的时间来覆盖外加航班.

如果一个方案可以被执行，那么它必须满足一系列可行性的条件.这些条件与衔接时间、总飞行时间和总运行时间有关.当一个机组配对模型可以得到大量的这种可行性方案时，就认为该模型具有鲁棒性.由于方案背后的主要思想以及相应的可行性条件是相似的，因此只列举一种A类型的方案和一种B类型的方案.

两个配对要形成一个A类型的方案，当且仅当这些配对在交换后是可行的.用p∈p表示连续覆盖航班i1和i2的配对，q∈p表示连续覆盖航班j1和j2的配对(见图2).如果这两个配对的机组来自于相同的基地，并且它们也满足某些可行性条件，主要是关于相对的抵达和起飞时间和交换航班之间的衔接时间，则p和q为外加航班k形成一个A类型的方案.交换之后，第一个配对由航班i1之前的航班、航班i2以及航班j2及其之后的航班组成，这里外加航班k被插入在航班i2和j2之间.同样，第二个配对由航班j1之前的航班、航班j1以及航班i2及其之后的航班组成.我们用pA(k)表示为外加航班k形成可行的A类型方案的配对对(p，q)的集合：

pA(k)={(p,q):q∈p为外加航班k形成一个A类型方案}.

图2中列举了一种带有一个置位机组的A类型方案.只有配对对(p，q)满足下面的可行条件，方案(A.1)才可以被执行.

(A.1)

在(A.1)中前两个条件保证航班i2和外加航班k之间的衔接时间和航班k和随后的航班j2之间的衔接时间都在可允许的限制范围之内.第三个条件对原始配对p的总飞行时间和总运行时间施加限制.最后一个条件是对原始配对q的总飞行时间和总运行时间的限制.

图2 带有一个置位机组的A类型方案(A.1)Fig.2 A sample (A.1) solution on the flight network with one deadhead

B类型方案只需要一个配对.如果一个被选择的配对有充足的衔接时间来覆盖外加航班，并且配对涉及的机组的剩余工作计划不会违反相关约束，那么这个配对就构造了一个B类型的方案.同样，通过检查各种不同的可行性规则来确保一个方案的有效性.为外加航班k形成B类型方案的配对集合可以表示为：

pB(k)={p∈p:配对p为外加航班k

形成一个B类型方案}.

图3举例说明了B类型方案的一种情况.只有配对满足下面可行性条件时，方案(B.1)才能够被实施.

(B.1)

图3 一种B类型解决方案(B.1)Fig.3 A sample (B.1) solution on the network with one deadhead

3 数学模型

在文中，提出了两种旨在安置外加航班的鲁棒性模型，模型的目标是使最优解中的配对尽可能多地为外加航班构造A或B类型的方案.隐含的假设是：随着最优解中配对构造的A或B类型方案数量的增加，计划在应对外加航班时将更具有鲁棒性.然而，该做法将导致在被选择的配对中会有更长的衔接时间，结果将导致总成本比传统模型(1)的要更高.为了权衡这两个方面，首先求解传统的机组配对模型(1)，得到它的最优目标函数值，用Copt表示.然后增加一个总成本约束到改进后的鲁棒性模型中，使得被选择配对的总成本不超过Copt的某个百分比，这个百分比是人为设定的.

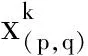
在模型中，配对p的成本cp用公式cp=max{fp*Te(p),nd*mg.∑d∈pcd}计算，Te(p)是配对p的总运行时间，fp是一个纯小数，nd是配对p中勤务的数量，mg是一个勤务期的最小保证时间，cd是配对中勤务d的成本.同样，勤务期的成本cd=max{Tf(d),fd*Te(d),mg}，Tf(d)和Te(d)分别表示勤务期d的总飞行时间和总运行时间.注意到一个配对的成本都是由时间定义的.则鲁棒性模型为：

(3)

(4)

(5)

(6)

(7)

(8)

yp∈{0,1},p∈p.

(9)

模型(2)的目标函数是最大化A类型和B类型方案的总数量.约束(3)是集划分约束；约束(4)是确定A类型方案形成的条件，(p,q)∈pA(k)且配对p和q是解的一部分；约束(5)是确定B类型方案形成的条件，p∈pB(k)且配对p是解的一部分；约束(6)是使所选配对的总成本在一个可接受的范围内.

模型(2)并没有试着为每一个外加航班提供一个解决方案，而且虽然模型的最优解可能会为某些外加航班提供几种解决方案，但它可能不会为某个外加航班提供任何解决方案，即使这种可供选择的最优方案存在.在这种情况下，可以把下面的约束加入到模型(2)中，nblow表示每一个外加航班所需要的解决方案数量的一个下界.

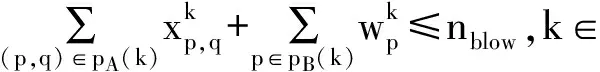
作为一种选择，也可以求解模型(3)，它把最大的值作为最优化目标函数值.该目标函数旨在尽可能公平地为外加航班分配解决方案.相比于模型(2)，模型(3)的目标函数和增加的约束如下：

maxz

(10)

注意到模型(2)和(3)都没有考虑任何防止一个配对出现在几个A或B类型的方案中的约束.当一个外加航班的两种不同的解决方案共享一个配对时，不会产生冲突.然而，如果一个配对不止为一个外加航班构成解决方案时，将面临两个外加航班在同一天被插入到航班计划表中的问题.这个问题称作重复计算.图4是一个重复计算的例子，有三个配对A，B和C，分别覆盖航班a1-a2，b1-b2和c1-c2，外加航班由k1和k2表示.在这个例子中，配对C和配对A为外加航班构造了一个A类型方案，同时配对C和配对B也为外加航班构造了一个A类型方案.在模型(2)中这两种方案将分别计入方案总数中.然而，如果航班和必须在同一天执飞，那么只能用配对C来覆盖其中的一个外加航班.

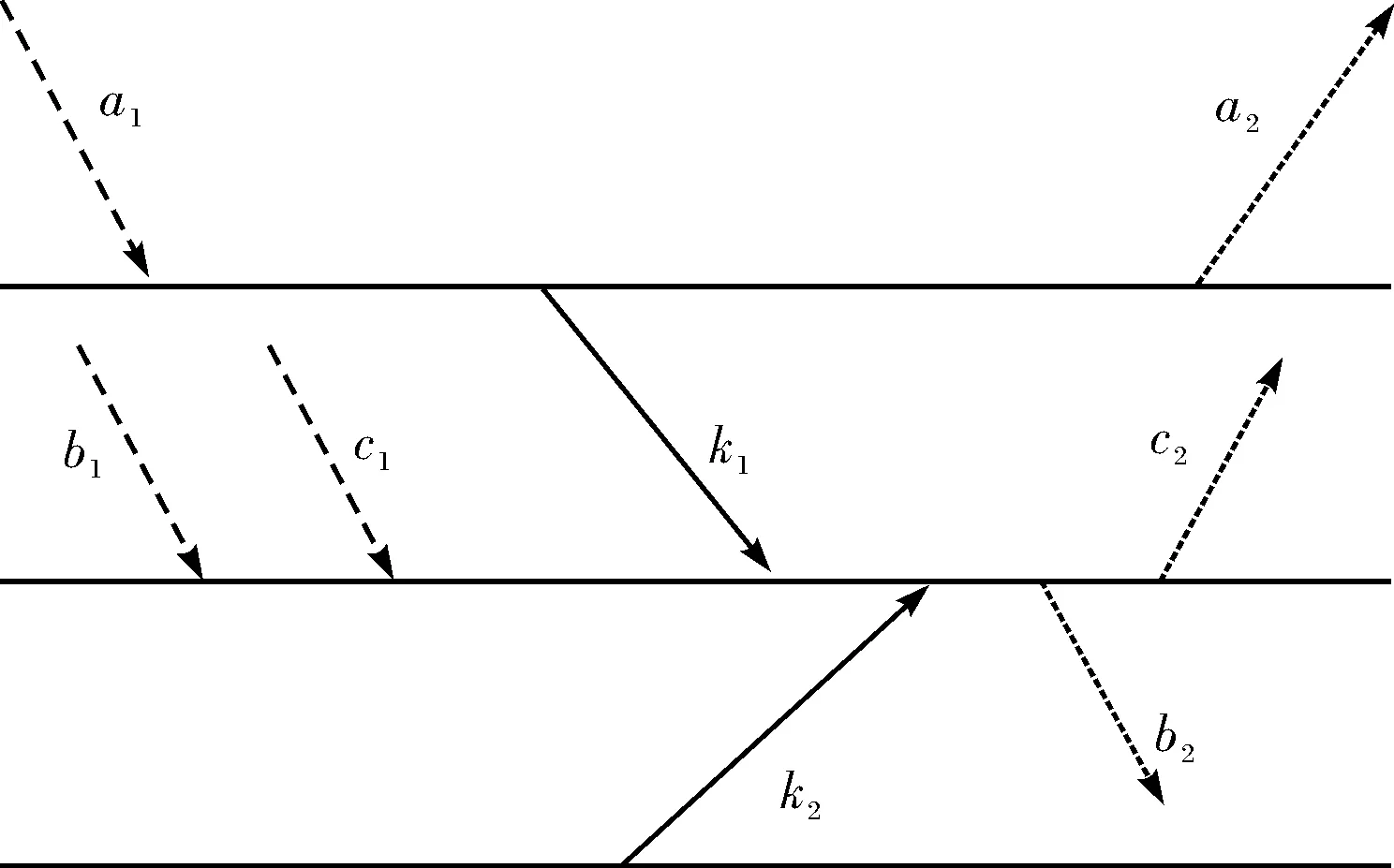
图4 一个重复计算的例子Fig.4 An illustration of the double counting problem

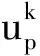
(11)

(12)

模型(4)与模型(2)一样都是最大化A和B类型解决方案形成的数量，但是模型(4)限制了一个给定配对怎样为一个给定外加航班和多个外加航班形成解决方案.约束(11)使一个配对至多只能出现在个解决方案中；约束(12)表示一个配对只能出现在一个外加航班的解决方案中.与模型(3)相比，模型(5)增加的新约束有：

(13)

(14)

4 算例分析

本文的研究在于证明处理外加航班的鲁棒性模型的价值而不是求解大规模的数学规划问题，因此本文没有尝试用大规模的数学规划技术来求解模型.算例规模很小以致允许找到所有可行的配对.只考虑周期为一天的配对.文中的一些参数如表1所示.

在案例中，有58个航班往返于SH、NJ、LYG、HF、JN、HZ和FZ七个城市之间，其中SH是仅有的机组基地，共有10架飞机.航班时刻表如表2所示.

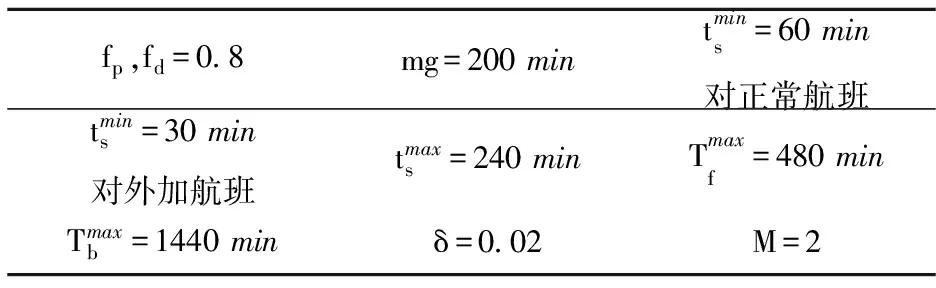
表1 配对形成中用到的参数

在这个问题中，从SH到NJ的航班和SH到HF的航班分别在15∶00和11∶25有很高的需求.为了满足这种需求，航空公司准备临时增开两个外加航班(SH-NJ)和(SH-HF)，两个外加航班的时间窗分别为15∶00-16∶30和11∶40-13∶30.

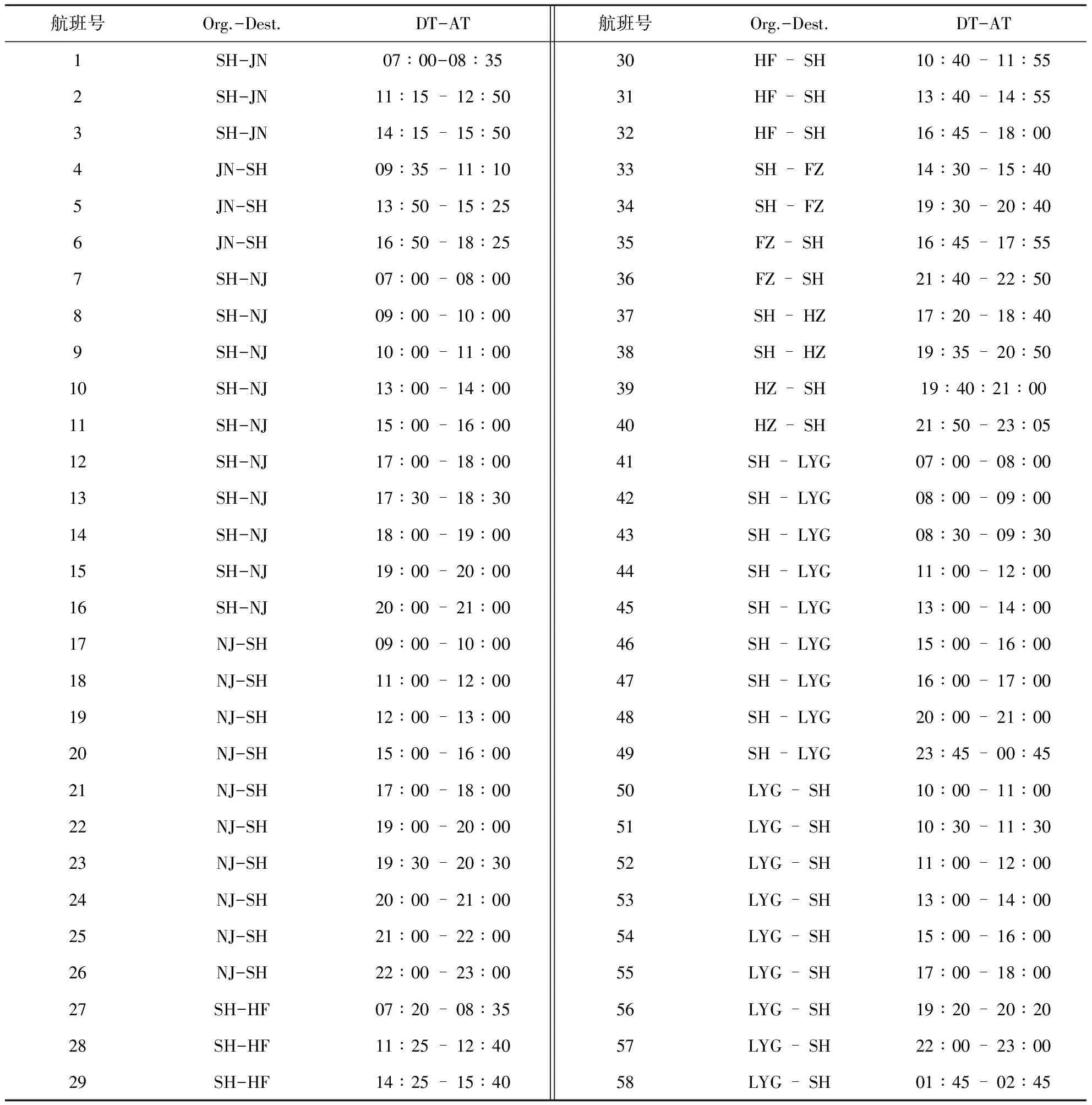
表2 58个航班的数据

用CPLEX 11.0在处理器为2.53GHz，内存为2GB的计算机上进行算例的求解.求得的结果如表3所示.从表中可以看到，鲁棒性模型得到的配对成本都比传统模型的高，但是都不高于传统模型的1.7%.在外加航班的覆盖上，CM(1)得到的最优化配对只能为外加航班k2构造方案；RM(2)则两个航班都可以被覆盖，但是需要注意的是，如果两个航班k1和k2同时被插入进来，那么航班k2只能用(91，970)来覆盖，因为(2108，1039)需要用来覆盖航班k2；RM(3)的解遇到了重复计算的问题，在两个航班需要同时插入时，它只能满足一个航班的需要.RM(4)和RM(5)都考虑了重复计算的问题，RM(4)得到的方案数量较多，但是有航班没能覆盖；RM(5)尽可能公平地分配方案，两个航班可以同时被插入.

从结果的分析可以得出，决策者可以根据遇到的实际情况来选择合适的模型.一方面，当所有航班不可能同时插入到航班计划中时，决策者可以选择忽视重复计算的模型以获得尽可能多的备选方案；另一方面，当同时覆盖所有航班对航空公司来说很重要时，决策者可以选择考虑重复计算的模型以获得尽可能覆盖所有航班的方案.同时，从表中可以看到模型的求解时间都很短，完全在航空公司可接受的范围内.

表3 由传统模型和各鲁棒性模型提供的恢复选择

5 结论及展望

本文在机组配对生成的计划阶段考虑了运营中可能遇到的临时航班加入的情况，构造了两种具有鲁棒性的数学模型.通过算例对模型进行验证，结果表明在为外加航班构造更多解决方案的同时，鲁棒性模型的机组配对成本均不超过传统模型的1.7%.同时，鲁棒性模型的求解时间在航空公司应对紧急情况的时间要求范围之内.不过，模型没有考虑外加航班对飞机排班和维修计划的影响，在今后可以把这方面的因素考虑进去做进一步研究.此外，文章还可以针对运用列生成算法求解大规模的机组配对模型做出一个更深层次的探索.

[1] Marsten R E， Shepardson F. Exact solution of crew scheduling problems using the set partitioning model: Recent successful applications[J]. Networks， 1981， 11(2): 165-177．

[2] Lavoie S， Minoux M， Odier E. A new approach for crew pairing problems by column generation with an application to air transportation[J]. European Journal of Operational Research， 1988， 35(1): 45-58．

[3] Beasley J E， Chu P C. A genetic algorithm for the set covering problem[J]. European Journal of Operational Research， 1996， 94(2): 392-404．

[4] 李耀华， 谭 娜. 飞机排班调度中机组指派优化模型及算法研究[J]. 计算机工程与应用， 2008， 44(34): 243-245．

[5] 肖真真. 基于任务均衡的航空公司机组人员指派问题研究[D]. 四川：中国民用航空飞行学院，2012．

[6] 鲁红珍. 航空公司机组航班任务串优化方法研究[D]. 四川：中国民用航空飞行学院，2012．

[7] Ehrgott M， Ryan D M. Constructing robust crew schedules with bicriteria optimization[J]. Journal of Multi-Criteria Decision Analysis， 2002， 11(3): 139-150．

[8] Shebalov S， Klabjan D. Robust airline crew pairing: Move-up crews[J]. Transportation Science， 2006， 40(3): 300-312．

[9] 牟德一， 张 婧. 具有鲁棒性的机组配对问题的随机规划模型[J].中国管理科学，2009， 17(6)：22-27．

[10] 牟德一， 王志新， 等. 基于机组延误概率的鲁棒性机组配对问题[J].系统管理学报，2011， 20(2)：207-212．

[11] Schaefer A J， Johnson E L， Kleywegt A J， et al. Airline crew scheduling under uncertainty[J]. Transportation Science， 2005， 39(3): 340-348．

[12] Yen J W， Birge J R. A stochastic programming approach to the airline crew scheduling problem[J]. Transportation Science， 2006， 40(1): 3-14．

[13] Anbil R， Gelman E， Patty B， et al. Recent advances in crew-pairing optimization at American Airlines[J]. Interfaces， 1991， 21(1): 62-74．

[14] Vance P H， Atamturk A， Barnhart C， et al. A heuristic branch-and-price approach for the airline crew pairing problem[J]. preprint， 1997，43(9):43-49．

Study on crew pairing for managing extra flights based on robustness

LE Meilong， ZOU Kaizhong

(Logistics Research Center， Shanghai Maritime University， Shanghai 201306)

In order to improve the service level of small and medium-sized airlines， enhance its flexibility to cope with extra flights， the article designs a new crew pairing solutions for extra flights. Based on the traditional model of the crew pairing， meeting the requirements of crew pairing for extra flights， we propose robust crew pairing model. Then through the example analysis， we used CPLEX software to solve the model， obtained the optimal solutions. Finally， through the comparison of different results， revealing the advantage of robust modeling method and showing that the proposed robust models provide natural options to recovery without disrupting the existing flights at a relatively small incremental cost， and providing meaningful reference for the small and medium-sized airline in the problem of coping with extra flights．

small and medium-sized airlines; extra flights; crew pairing; robustness

2014-09-03.

国家自然科学基金项目(71471110)．

乐美龙(1964-)，男，浙江宁波人，教授，博士生导师，主要从事物流管理与工程的研究.

*通讯联系人. E-mail: zzkkzzyy@163.com.

1000-1190(2015)02-0307-07

F550.74

A