有限元技术在汽车密封条结构优化设计中的应用

付治存

(上海长安汽车工程技术有限公司，上海 201114)

有限元技术在汽车密封条结构优化设计中的应用

付治存

(上海长安汽车工程技术有限公司，上海 201114)

主要论述有限元技术在汽车密封条结构优化中的应用。以ABAQUS有限元软件为基础，对密封条进行非线性有限元分析，获得密封条压缩变形形状、接触面上的压应力以及压缩受力变形特性，为进行密封系统的精益设计提供参考。

有限元技术；密封条；优化设计

0 引言

随着消费者对汽车乘坐舒适性的要求不断提高，防振、隔噪等密封性能方面的要求也越来越重要。借助有限元技术在设计阶段预先对密封条结构进行分析评价，提供改进优化措施，可以大幅降低产品的试制频次，提高产品的设计成功率，为密封性能的改善提供有力保证。文中以ABAQUS有限元软件为基础，应用有限元技术对某车型门框密封条进行分析评价，考察密封条在压缩过程中的变形、受力等情况，并对密封条结构进行优化，以满足设计目标要求。

1 软件简介

ABAQUS被广泛认为是功能最强的有限元分析软件之一，特别是在非线性分析领域，其技术和特点更是独树一帜，它融结构、传热学、流体、声学、电学以及热固耦合、流固耦合、热电耦合、声固耦合于一体，可以分析复杂的固体力学、结构力学系统，特别是能够驾驭非常庞大复杂的问题和模拟高度非线性问题。但是它在复杂的实体模型建模方面相对较弱，因此如果只用ABAQUS去完成复杂模型的建立、网格划分和求解比较困难。法国达索公司开发的CATIA软件是目前最流行的实体建模软件之一，它具有强大的实体建模和曲面造型功能。鉴于此，对于复杂模型的有限元分析，可以在CATIA软件中建立实体模型，通过ABAQUS软件与CATIA之间的接口，把模型导入到ABAQUS中进行网格划分、材料属性设置以及求解等操作。在这样一个有限元分析的过程中，不仅发挥了各个软件自身的优势，而且提升了分析的准确性，为复杂模型的有限元分析提供了一条新思路。

2 密封条有限元技术

密封条有限元技术是通过将离散化的密封条结构赋予材料力学性能，并应用有限元方法进行密封条刚度、强度和疲劳寿命分析的一种方法。

2.1 密封条的几何结构

门框密封条由EPDM密实橡胶、EPDM海绵橡胶和金属骨架3个部分组成，如图1所示。

(1)EPDM密实橡胶。硫化在“U”形金属骨架上，主要用以固定在侧围门洞止口上。

(2)EPDM海绵橡胶。海绵橡胶是密封条的最外侧部分，车门关闭时直接与车门接触，主要承受车门关闭时的压缩载荷，以产生密封性和回弹性，同时还可以弥补车门与车体之间间隙的不均匀性。

(3)金属骨架。在“U”形件中起夹持加强作用，并使密封条在压缩变形过程中保持正确的形状。

2.2 EPDM橡胶力学属性

进行密封条有限元分析之前首要的工作是获取EPDM海绵橡胶和密实橡胶的材料力学性能数据，数据越全面，表征的橡胶材料越真实，而据此设计的结构也越接近实际。

一般来讲，描述橡胶材料特性的基础实验有8种：单轴拉伸和压缩实验、双轴拉伸和压缩实验、平面拉伸和压缩(纯剪)实验以及测定体积变化的实验(拉或压)，如图2所示。

在长期的研究和实验中发现，从单轴拉伸、双轴拉伸、平面拉伸及体积压缩试验中能够获得足够精确的实验数据。因此，目前国际上定义橡胶材料力学行为的实验为：单轴拉伸(压缩)、双轴拉伸(压缩)、平面剪切及体积压缩。在这6种基本变形模式中，某些不同加载形式实际上具有相同的变形模式，因而是等效的。这是因为橡胶材料的不可压缩性允许静水压力叠加而不改变材料的变形。在单轴拉伸的基础上叠加适当的静水压缩，可得到双轴压缩的变形模式；在单轴压缩的基础上叠加静水拉伸可得到双轴拉伸的变形模式；在平面拉伸的基础上叠加平面应变的静水压缩可得到平面压缩的变形模式。

实际运用过程中，由于双轴拉伸、平面剪切、体积压缩数据不容易测得，所以提供完整的材料力学性能数据比较困难，多数情况下仅提供单轴拉伸(压缩)数据，这是目前做密封条有限元分析采用最多的、也是相对容易得到数据的方法。

2.3 EPDM橡胶材料本构关系

不同于金属材料仅需要几个参数描述其材料特性，橡胶材料行为复杂，本构关系是非线性的。对于各向同性的体积不可压缩或体积近似不可压缩的橡胶材料，其非线性弹性特性用超弹性本构模型描述，其本构关系采用应变能密度函数表示，而不是用弹性模量和泊松比。ABAQUS软件中提供了多种超弹性材料的应变能密度函数形式，如Arruda-Boyce、Marlow、Mooney-Rivlin、Neo Hooke、Ogden、Ploynomial、Reduce Polynomial、Van der Waals、Yeoh，其中Mooney-Rivlin和Ogden是EPDM密封条橡胶有限元分析常用的应变能密度函数模型。

(1)Mooney-Rivlin应变能密度函数

Mooney-Rivlin应变能密度函数有2参数、3参数、5参数、9参数之分。EPDM密实橡胶通常由2参数应变能密度函数来表征：

W=C1(I1-3)+C2(I2-3)

式中：C1、C2是材料常数，其值由EPDM密实橡胶材料试验确定。

(2)Ogden应变能密度函数

EPDM海绵橡胶采用Ogden应变能密度函数来表征：

式中：J=λ1λ2λ3，λ1、λ2、λ3为右拉伸矩阵的特征值即主拉伸比；μn，αn，βn为材料常数，其值由EPDM海绵橡胶材料试验确定。

该函数的优点在于指数αn可以是任意实数，适应非线性数据的能力较强。理论上n没有上限限制，但一般不推荐使用n>3的值。

上述应变能密度函数中的材料常数可通过拟合材料的应力-应变实验数据得到。根据材料基本变形模式，可确定相应的实验应力-应变关系，对实验数据进行最小二乘法拟合，可得到超弹性本构模型的材料常数。最小二乘法拟合可使实验应力与计算应力之间误差的平方和最小：

2.4 单元划分及选择

根据密封条等截面的结构特点，在有限元分析中往往将密封条的载荷压缩变形简化为平面应变问题，即将三维问题简化为二维问题，从而大大降低了模型的规模，缩短了计算时间。对于二维模型，在ABAQUS中可以采用Quad(四边形)或Quad-dominated(四边形占优)进行网格划分：

(1)Quad(四边形)。模型的网格仅包含四边形单元；

(2)Quad-dominated(四边形占优)。模型的网格主要使用四边形单元，允许过渡区域出现三角形单元。选择该类型更容易实现从粗网格到细网格的过渡。

在进行网格划分时，增加网格密度可以提高计算结果精度，但当网格已经较密时，增加密度不但不能显著地提高结果精度，还会使计算量大幅度地增加，甚至诱发单元畸变而导致计算失败，如图3所示，因此应兼顾计算量和计算精度的要求，以能正确反映结构的形状为准，不宜片面追求计算精度。同时还应该注意避免网格的过分扭曲，否则易出现收敛问题。

2.5 有限元技术辅助设计流程

ABAQUS推荐的密封条有限元技术辅助设计流程如图4所示。可以看出：密封条辅助设计实质上是对密封条结构的多轮优化过程，且该过程在有限元技术范围内形成闭环，当结构相对成熟后，即满足刚度目标要求时，再交由设计人员做结构的局部完善，然后再次返给分析人员做刚度、强度分析。这样可以有效减少结构设计方面的反复，提高产品设计的精准度，加快产品设计过程。

相比其他有限元软件，ABAQUS推荐的设计思路有一个显著特点，它是先把整个数值模型(如材料、边界条件、载荷等)都直接定义在几何模型上，而不是像其他前处理器那样定义在网格单元和节点上，这样在修改网格时不必重新定义材料和边界条件等模型参数，尤其在处理复杂问题时，可以先简单地划分粗网格，得到初步的模拟结果，然后再在适当的区域进一步细化网格，从而节约时间提高效率。

3 应用案例

3.1 案例介绍

门框密封条通过密实橡胶和“U”形金属骨架安装于侧围门洞止口边缘上，对车门和侧围门洞之间的间隙进行密封，如图5所示。由于受制造偏差的影响，车门密封间隙存在至少±1 mm的公差，相应的密封条压缩量也会在±1 mm间变化，为保证车门密封效果的稳定、一致，需要控制密封条压缩量的改变对密封反力(即密封条压缩负荷)的影响不明显，即提高密封反力对制造偏差的容差度。已知该密封条压缩量理论值3 mm，公差±1 mm。

3.2 创建密封条有限元模型

首先在三维软件CATIA中创建密封条几何模型，该模型对密封条夹持部做了简化，然后导入ABAQUS中，生成密封条未变形时的有限元模型，在导入的同时定义该模型为可变形的平面二维模型，如图6所示。在部件功能模块(Part)通过2D草图做一条直线表示车门刚体，以模拟车门的关闭状态。

3.3 创建密封条材料和截面属性

进入ABAQUS的“特性功能模块”(Property)，通过2D草图将密封条截面分割为海绵橡胶和密实橡胶两部分，分别为它们赋予材料特性和截面属性：海绵橡胶采用Ogden应变能密度函数来表征，材料常数根据单轴拉伸、平面剪切和体积试验数据取得，取n=3，其材料常数见表1。

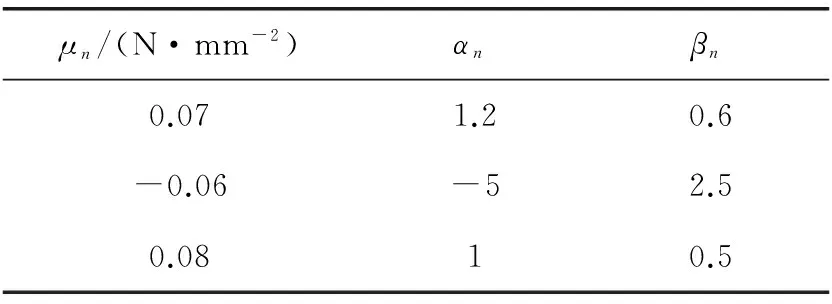
表1 海绵橡胶材料参数

密实橡胶采用Mooney-Rivlin应变能密度函数来表征，材料常数根据单轴拉伸和平面剪切试验数据拟合得到，其材料常数为：

c10=1.282 7 N/mm2

c01=0.321 7 N/mm2

3.4 装配部件，创建分析步

进入“装配功能模块”(Assembly)，将代表车门刚体的直线和密封条有限元模型装配在一起，如图7所示。

进入“Step功能模块”，创建接触和压缩2个分析步，选择类型为考虑几何非线性的通用静力学分析类型。

3.5 定义接触类型

在“相互作用功能模块”(Interaction)设置车门为刚性面，海绵橡胶为可变形面，建立面-面接触对，定义车门刚体是主动面，海绵橡胶是从动面，摩擦因数为0.2。

3.6 定义载荷和边界条件

进入“载荷功能模块”(Load),为密封条和车门的装配体创建边界条件，如图8所示。

密封条是可变形柔体，需要施加的边界条件是：固定夹持部位的密实橡胶X向位移U1和Y向位移U2，即U1=0,U2=0。

车门刚体需要施加的边界条件为：

(1)第一个分析步——接触。之前在创建代表车门刚体的直线时，该直线已经与海绵密封条处于相切接触状态，所以该步设置U1=0,U2=0,U3=0,使接触关系平稳地建立起来。

(2)第二个分析步——压缩。车门向下移动4 mm压缩密封条变形，即

U1=0,U2=-4,U3=0

3.7 划分网格，提交分析作业

进入“网格功能模块”(Mesh),从单元尺寸、单元形状、单元类型3个方面定义密实橡胶和海绵橡胶的网格划分，如图9所示。

(1)单元尺寸。分别选取密实橡胶和海绵橡胶的轮廓边线，设定单元大小：海绵橡胶因为尺寸相对较小，且是此次分析最关心的部分，所以单元尺寸设为0.3；密实橡胶尺寸相对较大，单元尺寸设为0.7。

(2)单元形状。鉴于三角形单元变形性能欠佳，单元形状选择四边形单元(Quad)。

(3)单元类型。选择线性(一次)单元(Linear),并开启非协调模式，即单元类型为CAX41,该类型能克服剪切自锁问题，且具有较高的计算精度。

进入“Job功能模块”，提交分析作业。

3.8 结果分析

分析计算完成以后，进入可视化模块，可以看到变形前/后的模型图、应力云图、应变云图以及压缩负荷与压缩位移的X-Y图表等信息。图10所示为密封条压缩4mm变形前/后的对比图。

从图10可以看出：变形较大的部位是海绵橡胶，根据作用力与反作用力原理它在变形的过程中也持续对车门施加了反力，起到了密封作用。如图11所示为密封条压缩4mm时的应力云图，其中应力最大的区域位于右侧根部，最大应力为0.071MPa，主要是由于受到较大弯矩引起的，如图12所示。

图11 密封条压缩4mm时应力云图 图12 最大应力局部图

从图13中可以看出：压缩负荷与压缩量的关系为非线性关系，虽然压缩量在3mm时的压缩负荷为3N，满足公司设计要求，但是以压缩量3mm为临界点，曲线发生了跳跃，导致压缩负荷大幅上升。这表明密封条压缩量在公差范围内的变化对密封反力(即压缩负荷)影响明显，该密封条结构降低了密封反力对制造偏差的容差度，影响车门密封效果的稳定性和一致性，也对密封条的寿命产生了较大影响，需要进行优化。

4 优化结构辅助设计

在对密封条结构进行优化设计时，主要对灵敏度较高的相关部位和尺寸进行优化。由前面分析已知，海绵橡胶右侧根部弯矩较大容易引起应力集中，因此，对密封条进行改进设计，将海绵橡胶右侧的弯曲角度减缓，增大圆角，使其自然过渡，同时将左侧根部区域的海绵泡管变薄，保证左右受力尽量均衡。如图14所示，虚线为密封条的初始结构，实线为优化之后的结构。

将优化结构重新导入ABAQUS中进行分析验证，得到应力云图、压缩负荷曲线等信息。从图15—16可以看出：结构优化以后应力集中区域面积大幅减少，最大应力为0.027MPa，比初始结构降低了62%，效果十分明显。

从图17所示的密封条压缩负荷曲线可以看出：密封条结构优化改进以后，压缩负荷有所上升，但仍在要求范围之内，可以接受；压缩负荷曲线变得平缓光顺，当压缩量在(3±1)mm的范围内变化时，没有引起曲线跳跃突变，即压缩量的变化对密封反力(即压缩负荷)影响不明显，有利于车门密封效果的稳定一致。由此验证了优化结构达到了设计目标要求。

图15 优化结构压缩4mm时应力云图 图16 优化结构最大应力局部图

5 结束语

密封性能问题一般都是在样车制作完成的阶段才暴露出

来，在此阶段，车门/车体结构、密封条结构等基本上已经设计定型，为改善密封效果再从结构方面着手进行改动，势必造成成本浪费甚至拖延项目进度。因此，在设计阶段提前改进优化密封结构尤为重要，在该阶段借助有限元技术合理设计密封条的截面和使用材料，才能有效减少甚至避免后期整改问题的费用和时间。

【1】陆明万，张雄，葛东云.工程弹性力学与有限元法[M].北京：清华大学出版社，2005.

【2】刘展.ABAQUS6.6基础教程与实例详解[M].北京：中国水利水电出版社，2008.

Application of FEM in the Optimization Design of Automobile Seal

FU Zhicun

(Automotive Engineering Institute of Chang’an Automobile Co.,Ltd.,Shanghai 201114,China)

The application of FEM in the optimization design of automobile seal was introduced. The nonlinear FEM analysis of automobile seal was carried out by using the FEM software ABAQUS. The automobile seal compression deformation shape, stress and deformation curves were gained. It provides reference for the design of the sealing system.

Finite element technology；Seal；Optimization design

2015-05-22

付治存，男，工程师，主要从事汽车闭合件设计。E-mail：zc3zc@163.com。