压缩机主轴－叶轮摩擦性能及过盈装配主轴弯曲变形研究

马国军，高俊福，郭 峰，谭 鑫，吴承伟＊

（1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连理工大学 工程力学系，辽宁 大连 116024；3.沈阳鼓风机集团股份有限公司，辽宁 沈阳 110869）

0 引 言

大型压缩机广泛应用于石油化工、冶金、空气分离、制药以及国防科研等各个领域，是国家基础工业的关键装备.由于运行工况复杂，压缩机运行的安全性与可靠性要求极高.转子系统作为压缩机的核心部件，其设计水平、加工和装配质量对整个压缩机系统的性能有着至关重要的影响.由于需要传递足够大的扭矩，叶轮与主轴往往通过加热叶轮来实现过盈装配［1－2］.这种装配形式具有结构简单、对中性好、承载能力强、抗冲击性能好等优点，但近年来随着压缩机大型化趋势的不断发展，过盈装配后的主轴容易产生弯曲变形，而且尺寸越大，弯曲越容易发生，程度也越严重［3］.显然，装配后主轴弯曲程度过大，必然使转子在实际运行过程中出现振动超标、噪声过大、碰磨以及失稳等一系列不良后果，因此如何避免大型压缩机主轴在装配过程中发生弯曲现象已成为企业急需解决的关键问题.

从力学的角度来看，主轴装配后之所以发生弯曲变形主要是因为受力不均，而导致受力不均的原因又可能与热装配过程中的温度场不均、材料性质不均、形状尺寸误差以及主轴－叶轮表面摩擦性质、过盈量等设计参数有关.或许是因为此前压缩机尺寸不是特别大时，主轴热装配后发生弯曲变形的概率较小，或即使发生程度也不是很严重，所以热装配后的主轴弯曲问题一直未引起足够重视，仅有少量资料可查.如王跃方等［3］在一份研究报告中曾对压缩机转子热装配后的主轴弯曲问题进行过数值模拟分析，他们发现前面提到的降温不均、加工误差、材料不均以及装配时的不规范操作都是可能导致主轴弯曲的原因，但他们在计算中假设轴的材料沿纵剖面一分为二为完全不同的材料，考虑降温不均时也只简单设置两种不同的热交换系数，与实际情况相差较大.Sun等［4］利用三维有限元模拟分析了加热温度、方式等对船用发动机曲轴过盈装配效果的影响，发现各部曲轴在装配时存在耦合影响，彼此间会引起曲轴整体发生弯曲变形.孟磊［5］曾指出减小轴向接触长度有利于防止主轴弯曲，但没有给出具体分析结果.

上述研究无疑对分析热装配后主轴发生弯曲变形的原因有着重要的指导意义，但所建模型过于简单或结构与压缩机转子差异较大，不足以解释或解决压缩机主轴装配时所遇到的弯曲变形问题.此外，上述研究也没有讨论转子大型化对主轴装配弯曲问题带来的新影响.显然，压缩机转子尺寸越大，工作时需要承受的离心荷载和所要传递的扭矩就越大，也就需要更大的过盈量来防止转子在工作时产生松动，同时保证主轴与叶轮交界面上有足够大的摩擦力来传递扭矩.然而，从所查阅的文献来看，有关过盈量对主轴热装配弯曲变形的影响规律研究还未见到，而有关压缩机叶轮常用材料FV520B 和主轴材料40NiCrMo7的摩擦性能方面的数据也未见到公开资料.

目前与转子装配相关的研究大多关注的是过盈量、摩擦力（摩擦因数）对转子接触压力、应力分布和传递扭矩的影响.如符杰［6］研究了不同过盈配合形式以及表面粗糙度等对传递扭矩和摩擦因数的影响，而沈健等［7］研究了叶轮－主轴在大过盈配合时的拆解过程，探讨了拆解力与过盈量、摩擦因数、热膨胀系数和温度之间的关系.Boutoutaou等［8］研究了结构形状误差或缺陷对装配压力的影响，发现允许形状误差的过盈装配设计能更好地满足工程实际.McMillan等［9］采用有限元计算和实验相结合的手段，验证了微滑移模型在预报主轴与轮毂紧固效果的有效性.Booker等［2］测量了以低碳钢为材料的轮毂－主轴过盈装配时的摩擦因数，发现表面粗糙度及纹理方向对摩擦因数有重要影响.Boutoutaou等［10］则分析了主轴表面粗糙度对过盈接触压力的影响.但正如前文所述，这些研究都未涉及当前压缩机主轴装配过程中的弯曲问题，因此本文首先通过实验测量压缩机转子叶轮材料FV520B 和主轴材料40NiCrMo7之间的摩擦因数，讨论法向接触压力和表面粗糙度对这两种材料摩擦因数的影响；然后通过三维有限元模拟，分析热装配过程中降温不均时不同过盈量和摩擦因数对装配后主轴弯曲变形的影响，讨论导致主轴热装配后发生弯曲变形的力学机理.

1 FV520B 与40NiCrMo7摩擦因数测量

1.1 实验材料及方法

将压缩机叶轮用材料FV520B 加工成直径16mm、高度10mm 的小圆柱，两个为一组，将圆柱试样其中一个端面用精密磨床进行精抛光，再用不同标号的砂纸打磨出不同粗糙度的表面，但同一组圆柱采用相同标号的砂纸打磨，使两个端面的粗糙度基本一致.主轴用材料40NiCrMo7加工成长120 mm、宽36 mm、厚10 mm 的块体试样，将面积最大的两个表面（120mm×36mm）也用精密磨床进行精抛光，然后用不同标号砂纸打磨，得到不同粗糙度的表面，但同一试样采用同一标号砂纸，以便尽可能保证同一试样的两个表面粗糙度一致.打磨后的试样采用时代集团生产的TR－200型便携式粗糙度仪进行粗糙度Ra测量，每个表面测试5 次，取平均值，然后再将同一组（圆柱体）或同一块（长方体）试样的粗糙度求和平均，以作为测试表面的粗糙度值.实验中长方体试样9块，粗糙度Ra分别为0.091、0.125、0.233、0.250、0.356、0.405、0.446、0.699和0.837μm，对应圆柱体试样43组.

测试采用的仪器为本实验室自行设计加工的专用摩擦因数测试仪，图1（a）和（b）分别为该设备的实物照片和原理示意图.实验时将一对FV520B圆柱体试样分别放在定位夹具⑧中的定位槽中，40NiCrMo7块体试样放在这两个圆柱体试样之间.通过旋转加力杠杆①转动加力丝杠②推动滑块⑥，使块体试样和圆柱体试样之间形成一定的法向压力，该压力的大小可通过力传感器⑤测量得出，由此可考察不同法向压力对摩擦因数的影响.将测试仪水平放置在电子万能试验机（原深圳新三思公司CMT4204 型电子万能试验机）的平台上，通过压缩夹具对块体试样施加如图1（b）所示的竖直方向的压力，并同时由计算机自动记录该压力随位移或时间的变化曲线，最大静摩擦力即为该曲线中第一个突然下降点对应的最大力值，再计算得到摩擦因数.圆柱体试样和块体试样实验前先用无水乙醇进行表面清洁，随后用吹风机烘干，以消除表面杂质和液膜的影响.

图1 摩擦因数实验仪器照片及原理示意图Fig.1 Picture and schematic diagram of the friction factor test apparatus

1.2 实验结果

图2（a）是实验过程中得到的典型力－位移曲线，纵坐标Fp对应于图1（b）中试验机沿竖向施加在块体试样的压力，Fp＿max为力－位移曲线中的最大力值，即静摩擦力；Fn对应于图1（b）中通过圆柱体试样施加在摩擦面法线方向的压力；Ra＿c为圆柱体试样的表面粗糙度，而Ra＿r为块体试样的表面粗糙度.从图2（a）可得到静摩擦力，除以法向压力（注：摩擦面为两个表面，所以单个表面的摩擦力为Fp＿max的一半）即可得到摩擦因数μ，具体为

图2（b）给出的是摩擦力在不同法向压力和不同粗糙度时的变化曲线，空心符号为测量得到的数据点，实线为拟合直线，根据式（1）可知拟合直线斜率的一半即为摩擦因数.可以看到，当法向压力小于约36kN 时（平均接触压强约为180 MPa），实验数据点与拟合直线非常吻合，意味着此时摩擦因数与法向压力无关.然而当法向压力进一步增大时，摩擦力略往上偏离拟合直线，即摩擦因数在法向压力较大时会增大.不过从图2（b）可以看出这种差异并不大，因此可将拟合直线的斜率视为不同法向压力作用下的平均摩擦因数，本文后续所述摩擦因数都由这种方法得到.从图2（b）还可看出摩擦因数对表面粗糙度较为敏感，当40NiCrMo7块体的表面粗糙度保持恒定（Ra＿r＝0.446μm），圆柱体FV520B 试样的表面粗糙度越大，图中拟合直线的斜率越大，即摩擦因数随Ra＿c的增大而增大.

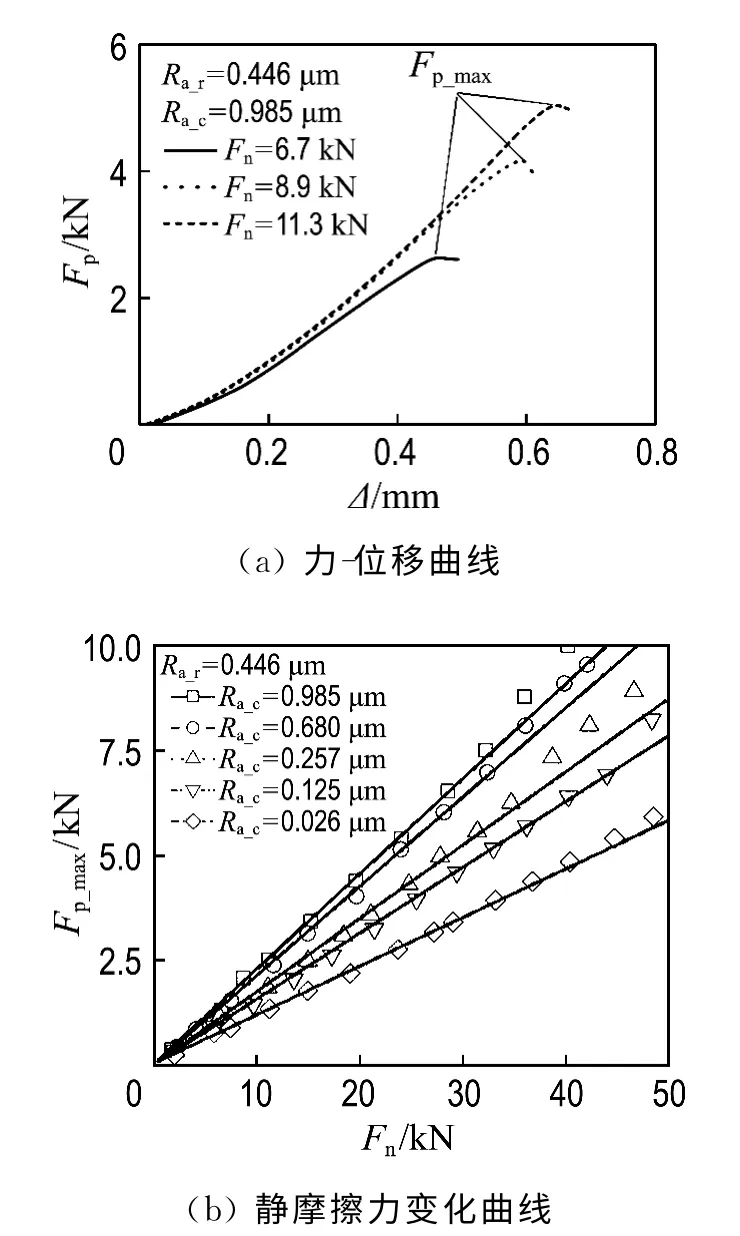
图2 圆柱体试样的力－位移曲线和在不同法向压力作用下的静摩擦力变化曲线Fig.2 Typical force－displacement curves of the column－like samples and changing curves of static frictional forces with different normal compressive forces

图3是测试得到的全部43个数据点，纵坐标是摩擦因数，横坐标是圆柱体试样表面粗糙度Ra＿c，图 中 空 心 符 号 形 状 的 不 同 表 征Ra＿r值 的 不同.可以看到这两种配对材料的摩擦因数范围在0.12～0.25，虽然数据有一定的离散性，但大体趋势表明随着圆柱体FV520B试样表面粗糙度Ra＿c值增大，摩擦因数呈增大趋势，而随着块状40NiCrMo7试样表面粗糙度Ra＿r值增大，摩擦因数反倒减小.由摩擦学相关理论［11－13］可知，摩擦力产生原因主要有两点：（1）粗糙峰在一定压力作用下嵌入表面，产生犁沟效应，从而形成摩擦阻力；（2）表面粗糙峰发生接触变形而产生具有较强黏合力的黏着区，黏着区域越大和材料剪切强度越大，黏附力越强，摩擦力即为克服这种黏附力所需的力.根据已有资料可知，40NiCrMo7 大尺寸锻件的屈服强度为780～980 MPa，HB 硬度值为232～295；FV520B 的屈服强度为925～1090 MPa，HB硬度值为277～341.由于FV520B无论是强度还是硬度都要比40NiCrMo7高，FV520B试样表面粗糙峰在法向压力作用下会嵌入到40NiCrMo7中，产生犁沟效应.FV520B表面越粗糙，犁沟效应越强，所以摩擦力或摩擦因数就越大.相反，40NiCrMo7 试样表面的粗糙峰不会嵌入到FV520B材料中，而是产生局部弹塑性变形，形成黏着区，由此产生摩擦力.当40NiCrMo7试样表面越光滑，这种微黏着区域越大，即真实接触面积变大，结合力也就越强，从而使摩擦力和摩擦因数的值增大.图3中的插图为非常光滑的40NiCrMo7试样在实验后的宏观照片，可以看到在表面产生了非常明显的黏着区域.当40NiCrMo7表面粗糙度较大时，则观察不到这种现象，而且FV520B 试样上不论粗糙度大小如何都观察不到这种现象，其表面纹理在实验后无明显变化，也无材料附着.

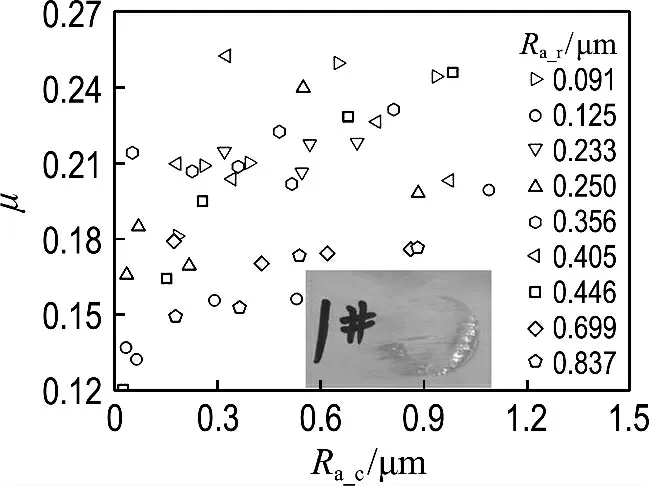
图3 表面粗糙度对材料FV520B 与40NiCrMo7摩擦因数的影响Fig.3 Influence of the surface roughness on the friction factor between the materials FV520Band 40NiCrMo7

2 主轴弯曲变形的有限元数值模拟

2.1 计算模型及方法

本文采用有限元软件ABAQUS进行某真实转子的热装配过程模拟，叶轮材料为FV520B，主轴材料为40NiCrMo7，图4为网格模型.进行网格划分时，考虑到叶轮结构复杂，采用几何适应性较好的四面体单元，主轴与轮盘轴孔部位发生接触，故采用一阶减缩积分单元（C3D8R），其他部分全部采用二阶四面体单元（C3D10），主轴则全部采用一阶减缩积分单元（C3D8R）.与此同时，为了提高计算精度和效率，在叶轮和轴的接触部位加密网格，最终叶轮网格数为66 652，主轴网格数为94 712.经过网格收敛性计算，这些网格数兼顾了精度和效率.在温度场计算时采用的网格为一阶六面体热传导单元（DC3D8）和二阶四面体热传导单元（DC3D10），与结构分析网格一一对应.考虑到实际情况和计算收敛性需要，采用如下边界条件：在主轴一端约束轴向自由度，同时在径向和切向施加一小刚度的弹簧约束；在轴的另一端，当主轴与叶轮未接触时，在径向和切向施加位移约束，以确保计算收敛，而一旦主轴和叶轮内孔接触，则解除该端全部位移约束，使轴可以产生自由弯曲；叶轮装配时假设放置在刚性平台上，与平台之间依靠摩擦来实现约束，摩擦因数设为0.1（转子实际装配时叶轮放置在一圆桶形装置的端面上，轴可以伸入其中，此平台模拟的即为该圆桶形装置的端面）.

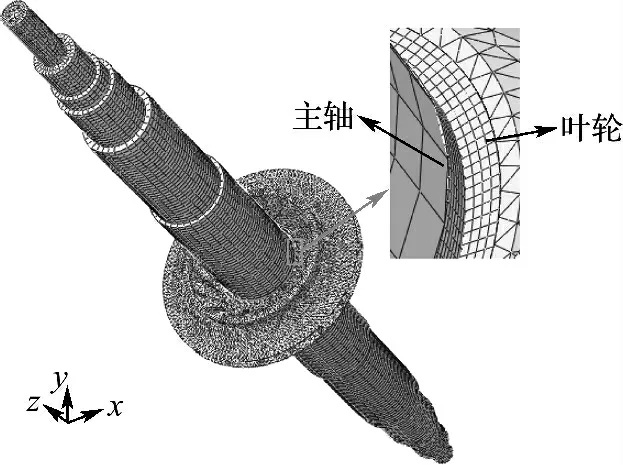
图4 叶轮－主轴有限元网格模型Fig.4 Finite element mesh model of the impeller and main shaft

实际调研发现，压缩机转子在装配过程中总存在不同程度的降温不均，可能是导致主轴弯曲变形的一个重要原因.因此，首先计算降温不均对主轴弯曲变形的可能影响.在计算时进行了以下简化：（1）转子与周围环境的热交换只考虑对流换热，忽略热辐射影响；（2）设装配体表面对流换热系数沿周向按余弦函数变化，以此来模拟温度场不均；（3）主轴与叶轮内孔表面的摩擦因数不随温度变化.上述假设与实际情况基本相符.叶轮装配前温度为330 ℃，主轴初始温度为室温（20 ℃），为了增大不均匀降温的程度以凸显出温度不均对弯曲变形的影响，适当扩大了空气强制对流换热系数，假设的对流换热系数按以下3种规律变化：（1）100×（0.75cosθ＋1.25）；（2）100×（0.5cosθ＋1.25）；（c）100×（0.25cosθ＋1.25），单位为W·m－2·K－1.下文将这3种降温条件分别记为Case＿1、Case＿2和Case＿3，Case＿1表示的降温不均程度最大，Case＿3 表示的降温不均程度最小.当转子最高温度降至室温20℃时计算停止，整个降温过程大约需要3h，这和实际情况基本符合.

2.2 温度场不均、摩擦因数和过盈量对主轴弯曲变形的影响

图5为上述3种降温条件下主轴弯曲变形随时间的变化曲线，计算中主轴与叶轮内孔表面的摩擦因数假设为0.1（该值是企业进行过盈装配设计时使用的推荐值，显然比前面所得到的实际摩擦因数要小，偏于安全），过盈量为0.244%，主轴长度为3.34m，这些数据为企业所提供.由图5可以看出，随着时间变化，主轴弯曲变形先增大后减小，最终趋于稳定，但都不能完全消失（3 种情形残余弯曲变形量分别为13.72、8.54 和3.55 μm）.图6给出了在Case＿1降温条件下，相对过盈量仍为0.244%时残余弯曲变形随表面摩擦因数的变化情况，计算时有意将摩擦因数范围扩大，以便更好地讨论摩擦因数的影响规律.可以看到随着摩擦因数增大，残余弯曲变形快速增大，然后趋于稳定.当摩擦因数等于零时，计算得到的残余弯曲变形为1.2μm.经过仔细分析发现，此时残余弯曲变形之所以不等于零是由于计算时假设了轮盘与平台之间有一定的摩擦力，使主轴承受一定的横向力.若将轮盘与平台之间的摩擦因数设为0.01，而叶轮与主轴摩擦因数仍为0，计算得到主轴最终残余弯曲变形只有0.15μm，可认为是计算误差，即此时残余弯曲变形为0.上述结果说明摩擦力是主轴弯曲变形恢复的阻力，但并不能因此简单认为可通过减小摩擦来改善主轴热装配的弯曲变形问题，这是因为转子在工作时需要足够的摩擦力来传递扭矩，而且对大型和超大型压缩机而言所需传递的扭矩更大，往往还需要通过增大过盈量来增大摩擦力.因此图7给出了在Case＿1降温条件下，不同过盈量和不同摩擦因数共同作用对主轴残余弯曲变形的影响.可以看到当摩擦因数等于或大于0.1以后，主轴弯曲变形随过盈量的增大呈现出先增大后减小的趋势，这与此前人们认为过盈量增大会导致主轴残余弯曲变形增大的常规认识完全不同［3］.此外，从图7中还可看出，当过盈量小于某个临界值（本文为0.257%，但转子不同该值可能有所不同），摩擦因数的增大会导致主轴弯曲变形增大，而当过盈量大于该值后，摩擦因数增大主轴弯曲变形反倒会减小.

图5 不同降温过程中主轴弯曲变形曲线Fig.5 Bending deformation curves of shaft during different cooling periods

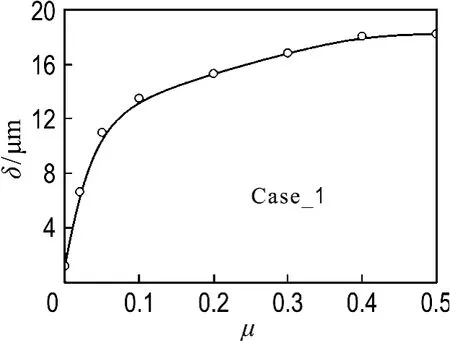
图6 主轴－叶轮摩擦因数对主轴弯曲变形的影响Fig.6 Influence of friction factor between shaft and impeller on bending deformation of shaft

图7 摩擦因数与过盈量对主轴弯曲变形的共同影响Fig.7 Coupling influence of friction factor and magnitude of interference on bending deformation of shaft

为了揭示导致上述现象的机理，不妨假设叶轮与主轴间的摩擦因数为零，叶轮与刚性平台间的摩擦因数仍为0.1，图7中最底下的直线即为残余弯曲变形随过盈量变化的计算结果.可以看到虽然残余弯曲变形绝对值很小，但却明显表现出随过盈量增大而单调减小的趋势，这说明若叶轮与主轴界面无摩擦力，过盈量增大只会有益于残余弯曲变形的回复.实际上若不考虑加工误差，叶轮是严格周期对称结构，所以冷却收缩后对主轴产生的接触压力也是严格周期对称的.在这种对称性的压力作用下，轴具有保持为直线的趋势，本质上是一种使轴由弯变直的作用力，所以过盈量增大，残余弯曲变形趋小.然而当摩擦因数不等于零时，过盈量的增大一方面会促使对称的法向压力增大，另一方面也会使切向摩擦力增大，残余弯曲变形实际是这两种相反作用的竞争结果.至于为何摩擦因数对主轴弯曲变形的影响会在过盈量大于某一临界值之后表现得完全不同，还无法通过简单的分析就能得出，但这一临界值的存在对于压缩机超大型的优化设计具有重要意义.进一步的计算还发现，若假设降温均匀，则无论主轴与叶轮以及叶轮与平台间的摩擦因数如何变化，主轴始终都不会发生弯曲变形，这说明装配过程中降温不均是导致主轴弯曲变形的诱因，企业应采取相应措施改善转子装配环境，尽可能避免或减小降温不均.

3 结 论

（1）FV520B和40NiCrMo7两种材料的摩擦因数在0.12～0.25，研究表明当法向接触压力小于约36kN时，摩擦因数与法向接触压力无关，但法向接触压力大于该值之后摩擦因数会轻微增大.

（2）摩擦因数的大小与材料表面粗糙度密切相关，当FV520B表面粗糙度增大时，摩擦因数整体表现出增大的趋势，当40NiCrMo7表面粗糙度增大时，摩擦因数反倒减小.产生这种现象的原因与粗糙峰的犁沟效应和微黏着效应有关.

（3）热装配过程中的降温不均是导致主轴装配后存在残余弯曲变形的诱因，摩擦力是阻碍弯曲变形回复的作用力，而由过盈所产生的法向接触压力是促使弯曲变形回复的动力.

（4）在所计算的范围内，过盈量存在临界值，当过盈量小于该临界值，摩擦因数越大残余弯曲变形就越大，但当过盈量大于该临界值，摩擦因数增大残余弯曲变形反倒减小，这对压缩机的大型和超大型化设计具有重要意义.

［1］ 杨树华，侯秀丽，王 宇.离心压缩机叶轮过盈接触及传递扭矩研究［J］.风机技术，2014（3）：40－43.YANG Shu－hua，HOU Xiu－li，WANG Yu.Study on interference contact and transmission torque for centrifugal compressor impeller［J］.Compressor，Blower ＆ Fan Technology，2014（3）：40－43.（in Chinese）

［2］ Booker J D，Truman C E.Measuring the coefficient of friction for use in shrink－fit calculations ［J］.Experimental Techniques，2011，35（2）：7－13.

［3］ 王跃方，刘万青，李 永，等.转子套装过盈应力、变形计算［R］／／沈鼓－大工研究院科研项目报告.大连：沈彭－大工研究院，2007.WANG Yue－fang，LIU Wan－qing，LI Yong，etal.Stress and deformation computation of rotor during shrink fit ［R］／／ Program Research Report of Shengu Co.，Ltd.and Dalian University of Technology.Dalian：Shengu Co.，Ltd.and Dalian University of Technology，2007.（in Chinese）

［4］ Sun M Y，Lu S P，Li D Z，etal.Threedimensional finite element method simulation and optimization of shrink fitting process for a large marine crankshaft［J］.Materials and Design，2010，31（9）：4155－4164.

［5］ 孟 磊.面向广义质量的闭式叶轮部装结构1＋3＋X 设计方法研究［D］.沈阳：东北大学，2007.MENG Lei.General quality－oriented 1 ＋3 ＋X designing method of the assembly structure of the shrouded impeller ［D］.Shenyang：Northeastern University，2007.（in Chinese）

［6］ 符 杰.过盈配合的摩擦系数研究［D］.大连：大连理工大学，2007.FU Jie.The research on interference fitted friction coefficient ［D］.Dalian：Dalian University of Technology，2007.（in Chinese）

［7］ 沈 健，郭长福，周 丹，等.大过盈配合的叶轮－主轴温差拆解机理的研究［J］.合肥工业大学学报（自然科学版），2015，38（1）：7－10，68.SHEN Jian，GUO Chang－fu，ZHOU Dan，etal.Study of temperature difference dismantling mechanism of large interference fitted impellerspindle ［J］.Journal of Hefei University of Technology（Natural Science），2015，38（1）：7－10，68.（in Chinese）

［8］ Boutoutaou H，Bouaziz M，Fontaine J F.Modeling of interference fits taking form defects of the surfaces in contact into account［J］.Materials and Design，2011，32（7）：3692－3701.

［9］ McMillan M，Booker J，Smith D.Validation of micro－slip in interference fitted shafts subject to complex loading regimes ［J］.Applied Mechanics and Materials，2011，70：351－356.

［10］ Boutoutaou H，Bouaziz M，Fontaine J F.Modelling of interference fits with taking into account surfaces roughness with homogenization technique ［J］.International Journal of Mechanical Sciences，2013，69：21－31.

［11］ Pavlescu D，Tudor A.Sliding friction coefficient—its evolution and usefulness ［J］.Wear，1987，120（3）：321－336.

［12］ 温诗铸，黄 平.摩擦学原理［M］.3 版.北京：清华大学出版社，2008.WEN Shi－zhu，HUANG Ping.Principles of Tribology ［M ］.3rd ed.Beijing：Tsinghua University Press，2008.（in Chinese）

［13］ Krim J.Friction at the atomic scale［J］.Scientific American，1996，275（4）：74－80.