人-机运动协调的矢量控制模型设计

金敉娜，谢光辉，王光建

（1.重庆电子工程职业学院，重庆401331；2.重庆大学机械传动国家重点实验室，重庆400044）

0 引 言

近几年，为保持机器人运动与人及环境的同步，人们利用阻抗控制方法对诸如搀扶、康复训练等人和机器人身体交流 (Physical Human-Robot Interaction)pHRI 运动的协调控制进行了较多的研究，且已取得一定的成果。在这些研究中，首先需要确定机器人和人谁是主控，谁是被控，然后由被控者来同步主控者的运动。实际上，人与人之间相互作用是自然的，不存在谁主控、谁被控，比如握手。故目前用阻抗控制的方法来实现人与机器人的自然交流有一定的难度。另外，神经元振荡器亦被应用于外骨骼助力机器人等pHRI 运动的协调控制上。虽然神经元振荡器能实现机器人与人各自的运动保持同步，但其内部有许多参数相互耦合，很不容易找到合适的参数匹配来实现同步，而且它只能适合于周期性运动场合。为进一步找到更简单易行的人-机交流运动的同步控制方法，这里提出了一种利用矢量构建的人-机运动协调控制模型，并对其特性进行了较详细分析。

1 矢量控制模型

1.1 吸引子

通常情况对于人形机器人来说，人类髋、膝和踝等各运动关节的角度变化，是由各感知器官根据外界环境变化并结合大脑内部状态自然而然地产生的。可以用式（1）来表示这种信息处理方式。

在此，X[k]∈RN表示在N 维空间里k 时刻机器人运动轨迹的状态向量，U[k]表示在k 时刻各关节输入信号，k=1，2…m 表示离散时间。如果这个动力学有一个与机器人运动（关节角度）相应的封闭曲线，离散样点X[k]会逐渐收敛于曲线。

假设封闭曲线Ξ 由式(2)、(3)组成。

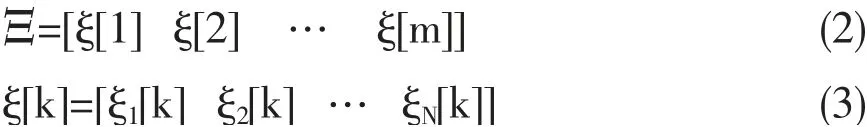
其中，ξ1[k]，ξ2[k]…ξN[k]表示机器人在k 时刻各关节角度。

图1 示出了N=3 的简单例子，三个时间序列数据ξ1、ξ2和ξ3组成了一封闭曲线Ξ，在此可把它称作吸引子。

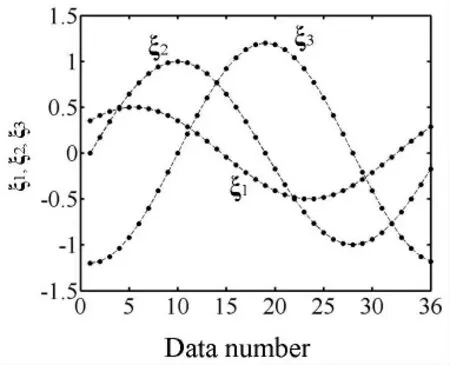
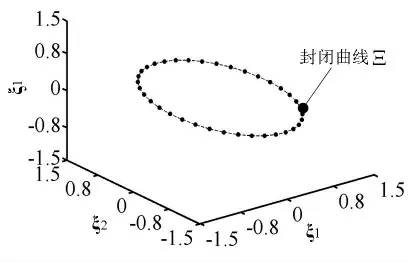
图1 时间序列和封闭曲线

1.2 矢量场构建

根据上文，我们可以设计一个如式(4)所示的非线性矢量控制模型⊅。

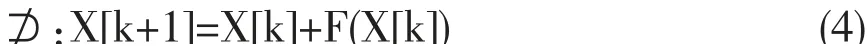
为了让式(2)所表示的曲线成为该控制模型的吸引子，可以在三维空间区域zZ 内按如图2 和式(5)定义如图3 所示的矢量场，其中i=1,2…，s。

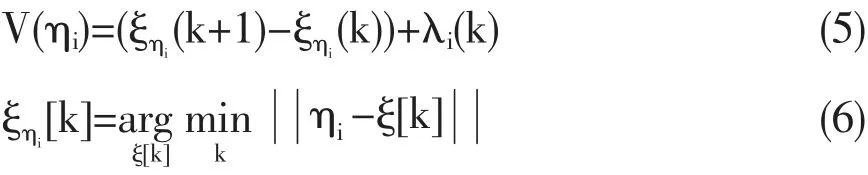
通过式(6)，可以在封闭曲线各离散样点中先确定与ηi最近的点，然后满足式(7)这样的充分条件以使该封闭曲线成为控制模型吸引子。

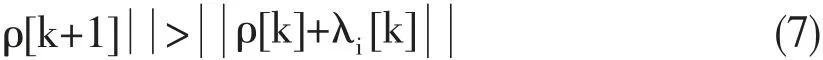
要满足此条件，只有当k→∞时，ρ[k]→0。

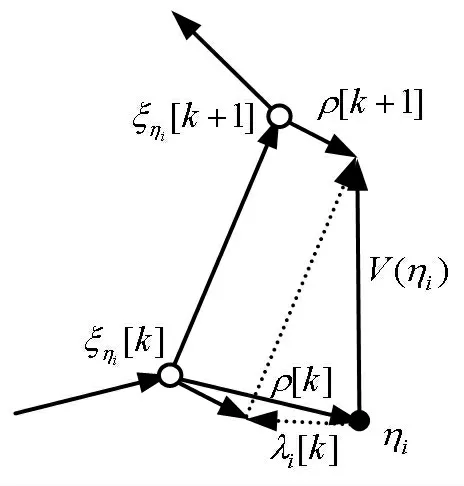
图2 矢量定义

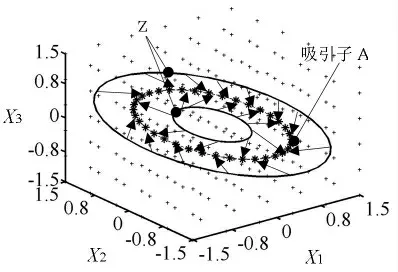
图3 矢量场定义

对于式(5)所提出的矢量场V(ηi)，可以用x 的多项式去近似它。当X∈R3，多项式如下：

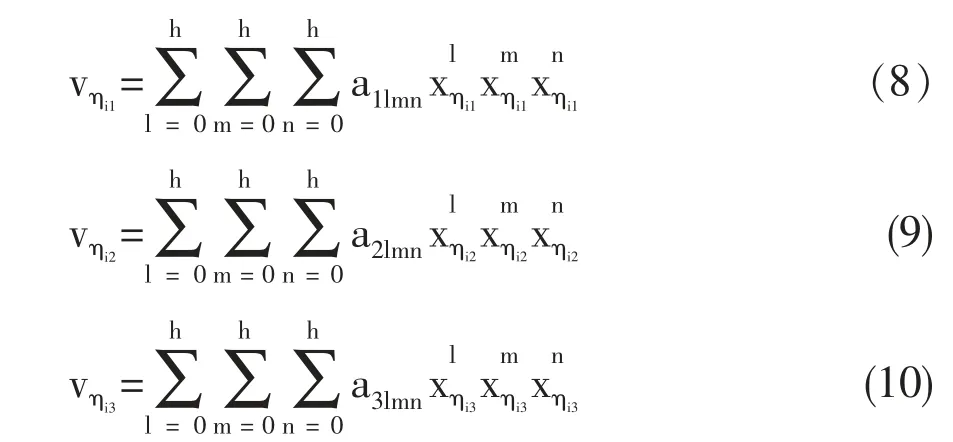
当Vηi1=（vηi1，vηi2，vηi3）T，Xηi1=（xηi1，xηi2，xηi3）T时，常数a1/mn、a2/mn和a3/mn可以通过最小二乘法计算得到。

0≤μ≤0 和0≤μ≤1 为矢量控制模型输入输出信号的同步调节系数，Θ#为矩阵Θ 的伪逆矩阵。

2 特性分析

2.1 参数影响分析

为分析上文所构建矢量控制模型的特性，在三维空间里按式(18)设计吸引子并建立相应矢量场。

其中，b 为振幅；ω 为角速度；X1和X2分别为输入和输出信号，此两者在理论上的相位相差0°。

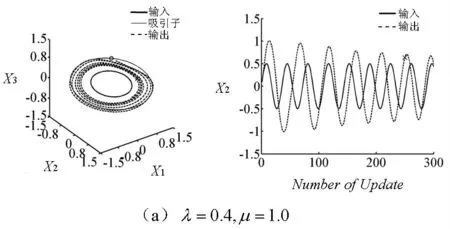
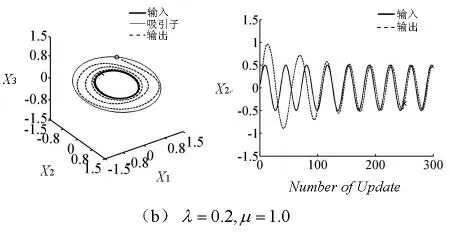
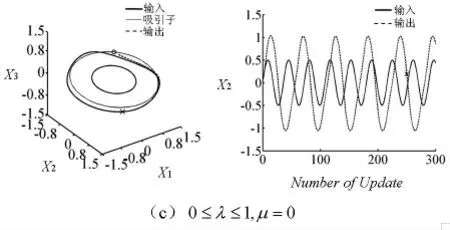
图4 参数λ 和μ 对同步的影响

矢量控制模型具有如下特性：

（1）根据矢量场设计和吸引子振幅的不同,分别可以得到频率和振幅不一样的输出信号。这可从图6(a)得出该特性，此处不单独以图示出。

（2）遗忘参数λ 对同步的影响。

输出信号随更新次数的推移逐渐与输入信号在频率、振幅及相位上取得同步，并且当遗忘参数λ(μ 恒定)越小时输入输出信号更易趋于同步。如图4(a)～(b)所示。

（3）同步阙值μ 对同步的影响。

输入输出信号是否同步决定于同步阙值μ，即当μ=0 时，输入输出始终不同步，图4(c)表明了这一结论；当0＜μ≤1，输入输出同步程度由大小决定。如图4(a)～(b)所示。

2.2 相互作用分析

上文对矢量控制模型进行了参数影响特性分析，而实际上力的作用是相互的，故有必要对两个不同的控制模型的相互作用情况进行分析。图5 示出了拥有不同矢量场的D1、D2两个控制模型的相互作用示意，D1模型的输出作为D2模型的输入，D2模型的输出作为D1模型的输入。 另外，在各自输出信号的原始频率和振幅两因素上，设计时考虑D1小于D2。

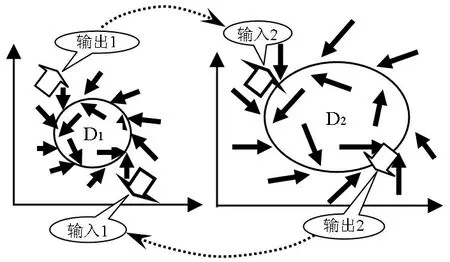
图5 相互作用模型

图6 示出了两个矢量控制模型在不同参数值下的相互作用结果：（图6 中“○”为输出1 和2的初始位置）

（1）如图6(a)所示，当μ1,2=0 时，无论λ1和λ2的比值如何（0≤λ1,2≤1，下省略），两模型各自的输出在频率、相位、振幅上都是不一致的；

（2）当0≤μ1,2≤1 时，无论λ1,2为何值，两模型各自的输出信号在频率、振幅上取得同步，这可从图6(b)～(d)得出该结论；

（3）两模型的同步输出信号逐渐收敛于值较小的系统输出。结果如图6(b)～(d)所示。

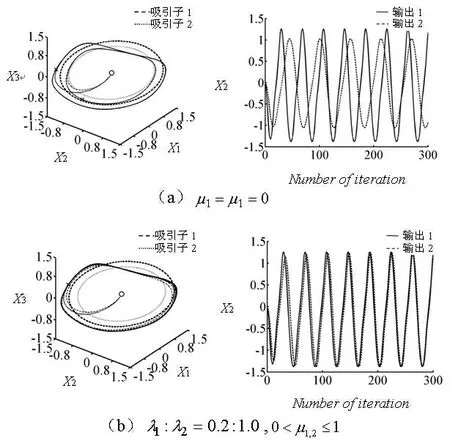
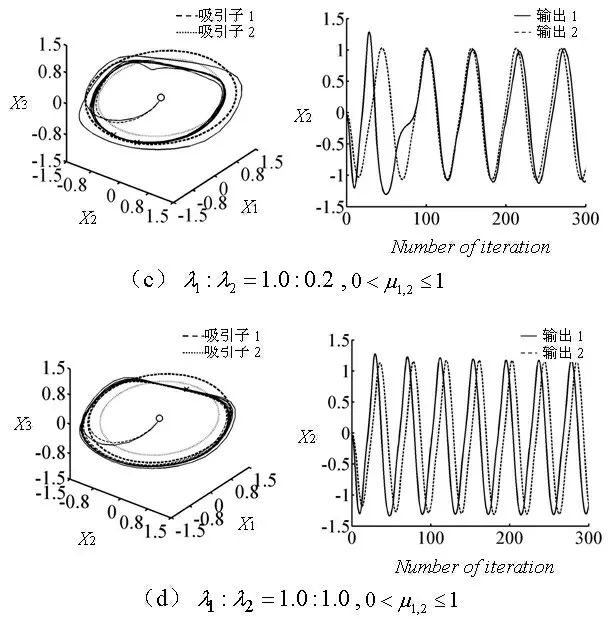
图6 相互作用结果

3 结 论

提出了一种基于矢量场构建的人-机运动协调控制模型，其输出可被用做机器人关节的规定轨迹，关节的相互作用扭矩信号被反馈到矢量控制器作为输入信号。同时，对该矢量控制器特性分析的结果表明，所提出的控制器能实现输入和输出信号在频率和振幅上的同步。另外，通过调节矢量控制器的遗忘系数， 可以调节同步的程度。此模型的有效性可用于人和机器人相互运动的同步控制研究，特别适用于诸如上肢外骨骼助力、跳舞、协助走和康复训练等具有周期性相互作用的运动，具有较大的价值。

[1]Ikeura R,Inooka H.Variable impedance control of a robot for cooperation with a human[A].Proceedings of the IEEE International Conference on Robotics and Automation [C].Piscataway,NJ,USA:IEEE,1995：3097-3102.

[2]Hirata Y,Takagi T,Kosuge K,et al.Motion control of multiple DR Helpers transporting a single object in cooperation with a human based on map information [A]. Proceedings of the IEEE Interanational Conference on Robotics and Automation[C].Piscataway,NJ,USA:IEEE,2002：995~1000.

[3]Kotosaka S,Schaal S.Synchronized robot motion by neural oscillators[J].Journal of the Robotics Society of Japan,2001,19(1):116-123.

[4]谢光辉,梁锡昌,等.基于同步控制的人和机器人握手动力学仿真[J].机器人,2008,30(5):428-434.

[5] Okada M, Tatani K, Nakamura, Y. Polynomial design of the nonlinear dynamics for the brain-like information processing of whole body motion[A].Proceedings of the IEEE Interanational Conference on Robotics and Automation[C].Washington D.C.,USA:IEEE,2002:1410-1415.