不同电场强度下Au 取代二元胺DAPDI 结构和性质的理论研究

张 坚，郭 莉

(山西师范大学化学与材料科学学院，临汾041004)

1 引 言

硅基集成电路在已过去的20 世纪给世界带来了巨大的变化，同时电子设备微型化的趋势使得传统的电子设备越来越受到量子效应和其它因素的影响. 为了解决这个困难，科学家们目前正致力于研究分子电子学，这个领域主要关注电子在分子中的传递［1-3］. 为了能组装成纳米级的电子电路，所需的分子导线应具有恰当的结构、能隙、偶极矩，同时还应当考虑分子导线对外电场的响应情况. 电流在电路上的传导需要自由的电子，因此分子导线的电学性质依赖于该共轭体系中π电子的离域情况［4］.

自从Ratner 和Aviram［5］首次在理论上证明了有机分子能够具备分子二极管的功能后，把有机分子用作电子器件的功能单元这一理念引起了很大的关注. 得益于新型实验技术的发展，近年来分子电子学出现了很多新兴的研究领域［6，7］. 越来越多的工作聚焦于分子导线的结构及其电子传输性质. 最近有一些相关报道:通过理论方法得到累积多烯的几何结构并通过对其分子轨道能的分析得出电位降［8］;对在外电场作用下的聚乙炔分子导线进行了理论研究［9］;Schab -Balcerzak 等［10］实验合成了一种具有电活性的新型二元胺N，N'—bis (4—amino—2，3，5，6—tetramethylphenyl)phtalene—1，2，4，5—dicarboximide (DAPDI).

分子的几何结构和电学性质会被外加电场所影响，因此为使分子能够成为电路中的组成部分，深入探讨在外电场作用下的分子的特性变化、考察分子导线的几何和电子结构是非常必要的［11-13］.

2 计算方法

本文基于密度泛函理论，对分子导线Au 取代二元胺N，N'—bis (4—amino—2，3，5，6—tetramethylphenyl)phtalene—1，2，4，5—dicarboximide

(DAPDI)进行了理论计算并探讨了其在外电场作用下的分子几何、电子结构、偶极矩、前线轨道、静电势等情况. 全部计算采用Gaussian09 程序包［14］，计算中使用Field 关键词，例如Field=X+10 为在分子的+X 方向施以强度0.052 VÅ-1的外电场，共考察了-0.416 VÅ-1到+0.416 VÅ-1区间中间隔均为0.052 VÅ-1的17 个外电场下的分子相关性质. 研究中采用B3LYP 杂化泛函方法，对重金属原子Au 选取LANL2DZ 基组，其它原子选取6 -31G* 基组. 几何优化过程使用内坐标的Berny 算法，最大受力和方均根受力的收敛阈值分别为0.00045 和0.0003. 分子的优化结构、前线分子轨道、静电势图像使用GaussView5 程序绘制［15］.

3 结果与讨论

3.1 几何结构

分子导线Au 取代二元胺N，N'—bis (4—amino—2，3，5，6—tetramethylphenyl)phtalene—1，2，4，5—dicarboximide (DAPDI)分别处于零电场和最大外电场下的优化几何结构如图1 所示.

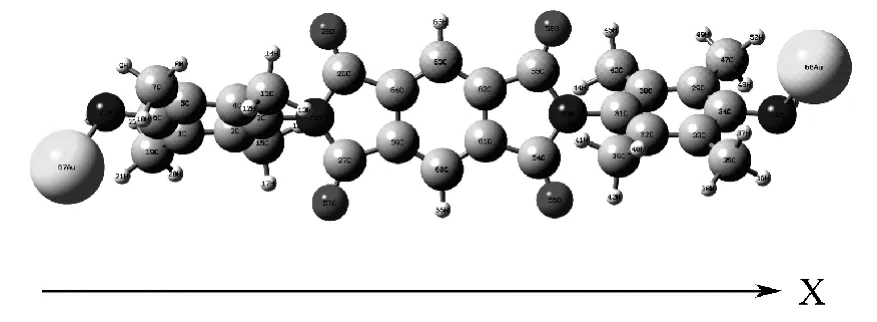
图1 零电场时的优化结构Fig.1 Optimized geometry at the zero EF intensities

键长，键角，二面角是重要的与分子导线的电学性质相关的几何结构参数，在表1 中列出了一些重要的几何参数优化数据，从中可以发现外电场并非对所有的键长都起着相同程度的影响.在X 轴正方向增强电场使N51—Au68键长变长，从2.07789 Å 增加到2.29948 Å，使Au67—N23键长变短，从2.07774 Å 减少到2.02999 Å;与此相反，在X 轴反方向增强电场使Au67—N23键长变长，从2.07774 Å 增加到2.28903 Å，使N51—Au68键长变短，从2.07789 Å 减少到2.03 Å. 该分子导线C—C 键长的整体变化幅度并不大. 键角方面相对零电场时的最大变化分别是，在X 轴正方向增强电场使键角Au67—N23—C6从115.99616°增加到137.43723°;在X 轴反方向增强电场使键角C34—N51—Au68从115.33864°增加到136.92978°. 二面角方面相对零电场时的最大变化分别是，在X 轴正方向增强电场使二面角Au67—N23—C6—C5从-78.14933°变为-15.42626°;在X 轴反方向增强电场使二面角C29—C34—N51—Au68从零电场的105.64002°增加到163.56614°. 以上二面角的变化主要是由于Au 原子的旋转造成的.

表1 零电场和最大外电场时的几何参数Table 1 Geometrical parameters at the zero and the maximum applied EF intensities

3.2 电荷分布

了解分子内电荷的分布情况对考察分子的化学反应活性，静电势，分子内相互作用都有着重要的作用［16］. 由于施加了外电场，分子导线中的每个原子的点电荷都可能会发生变化，进而引起电荷所能决定的分子其它特性的变化. 因此研究外电场下电荷的重排对探讨分子导线的性质很有必要. Mulliken 原子电荷布居是普遍采用的一种能够精确处理含静电相互作用的理论方法［17］.

分析该分子导线在不同电场强度下的N 原子和Au 原子(图2a)，C 原子(图2b)的Mulliken原子电荷布居可知，随着外电场强度的增加，原子的电荷相对零电场时不断的发生着变化，在最大外电场时所有原子的电荷也同步达到了最大值.在场强较低时(| EZ| ≤0.156 VÅ-1)，几乎所有原子的电荷变化幅度都很小;在场强较高时(| EZ| ≥0.208 VÅ-1)，几乎所有原子的电荷变化幅度都很显著. 在X 轴正方向增强电场的结果是:Au67和N51的电荷大幅增加，Au68和N23的电荷大幅减少，同时C 原子中电荷相对零电场增加最多的是C6，逐渐0.22224 增加到0.31423，C 原子中电荷相对零电场减少最多的是C29，逐渐从0.08768 减少到0.06934;在X 轴反方向增强电场的结果恰好相反:Au68和N23的电荷大幅增加，Au67和N51的电荷大幅减少，同时C 原子中电荷相对零电场增加最多的以及减少最多的分别是C34和C5. 靠近该分子导线对称中心的N25和N53的电荷变化幅度不大. 总体上说，当外电场在±X 两个方向增强时，该分子导线几乎所有的原子电荷都对外电场很敏感.

3.3 电偶极矩

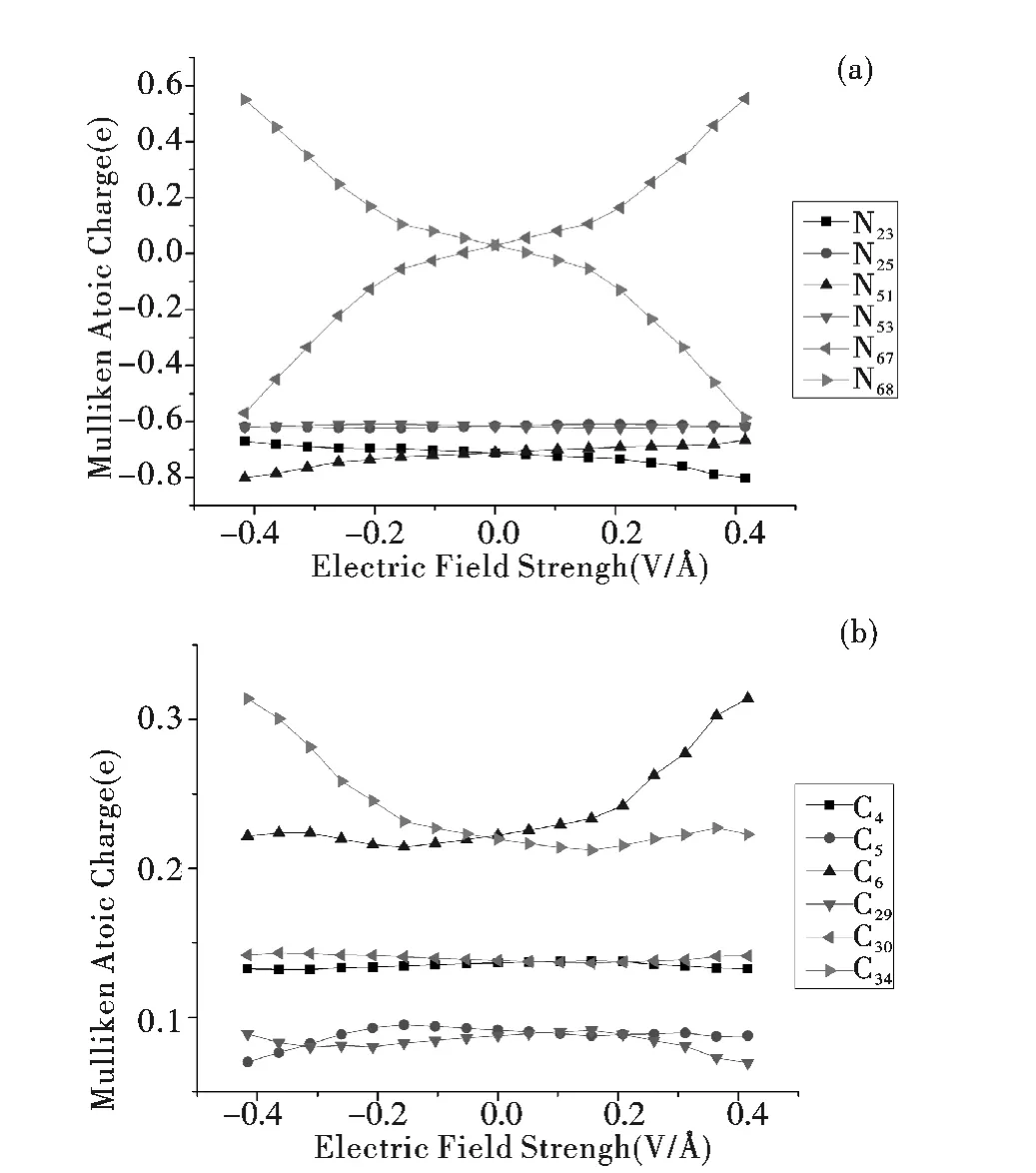
图2 不同电场强度下的Mulliken 原子电荷布居Fig.2 Mulliken atomic charges at various EF intensities

当分子处于外电场中，电场会将分子极化，这会导致分子的电偶极矩μ 发生变化. 分子的电偶极矩矢量的大小和方向是描述分子结构和电学性质的重要参数，因此确定在不同外电场下的分子电偶极矩是很有必要的. 最近Kirtman 等［18］分析了外电场作用下的电偶极矩并得出了线性规律.当然在超高强度电场下电偶极矩不会出现线性规律，而且一般的分子电子器件不能工作在超高强度电场下［19-23］. 图3 是该分子导线在不同外电场强度下的总电偶极矩μtot及其在XYZ 各方向的分量| μx| ，| μy| ，| μz| . 由于外电场的方向与X 轴方向一致，电偶极矩的X 方向分量是3 个分量中的主体部分，会随着外电场强度的增加呈线性的增加. 在高场下分子变得高度极化，分子的电偶极矩也就有了很高的数值. 在X 轴正方向增强电场的结果是，| μx| 和μtot分别从零电场时的0.0493 Debye 和1.0925 Debye 显著增加到最大外电场+0.416 VÅ-1时的75.6387 Debye 和75.6806 Debye;同样的情况也发生在X 轴反方向，| μx|和μtot分别从零电场时的0.0493 Debye 和1.0925 Debye 显著增加到最大外电场-0.416 VÅ-1时的74.2112 Debye 和74.3381 Debye. 从这些数据可以发现，随着外电场强度的增加，总电偶极矩μtot及其X 方向分量| μx| 会随之持续线性的增加.通过以上电偶极矩的显著变化可以明确的预知，如果加大外电场的强度，该分子导线与纳米电路的电极之间的相互作用会随之强烈的增加.

3.4 分子轨道分析

能隙是最高占据轨道(HOMO)与最低非占据轨道(LUMO)之差，其大小与分子中电子的迁移相关，因此考察在不同外电场强度下能隙和分子轨道能级的变化是很有必要的［24-27］. 图4 是该分子导线分别在零电场和最大电场强度下的分子轨道空间分布图，可以发现当外电场方向反转时，分子轨道的空间分布也随之变换方向，而且表现出相互对称的性质.

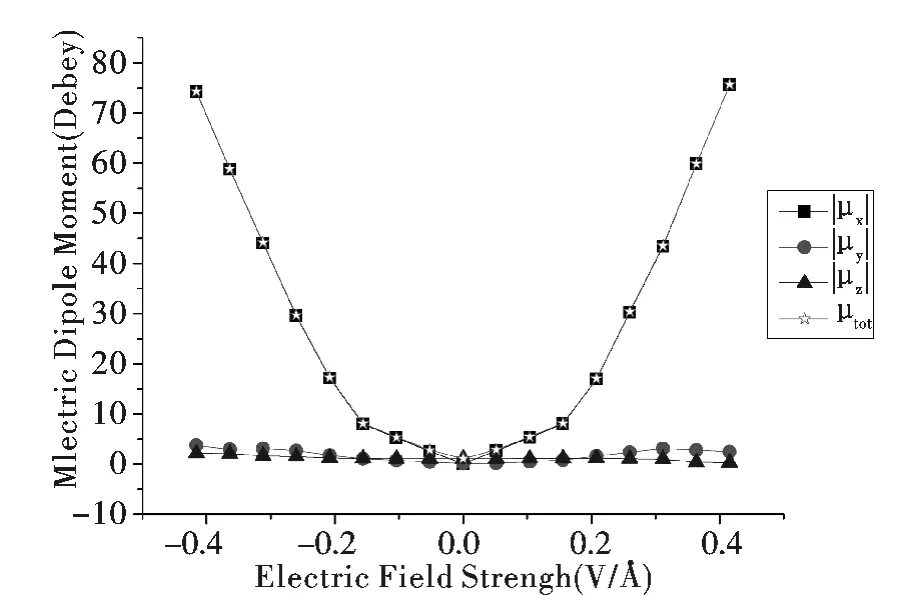
图3 不同电场强度下的电偶极矩Fig.3 Electric dipole moment at various EF intensities

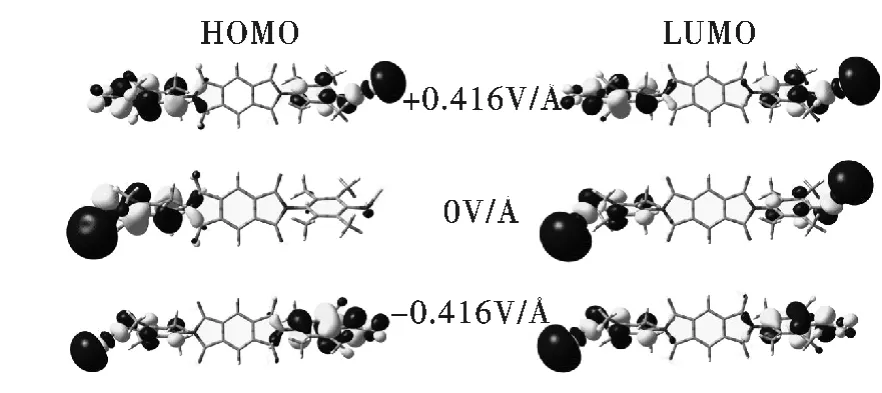
图4 零电场和最大外电场时的最高占据轨道与最低非占据轨道的空间分布图Fig.4 Spatial redistribution of HOMO and LUMO at the zero and the maximum applied EF intensities

图5a 是该分子导线在不同电场强度时的5 个占据轨道(O-1 ～O-5)和5 个非占据轨道(U-1 ～U-5)的能级图. 随着外电场在±X 两个方向的增强，O-1 (HOMO)能级与U -1 (LUMO)能级会对称的逐渐相互接近，另外也意味着能隙的逐渐减小. 值得关注的是，高电场强度下O -1与O-2，U-1 与U -2 之间存在较大的能级差.图5b 是该分子导线在不同电场强度下的能隙变化曲线. 零电场时能隙有最大值为0.09261 Hartree，随着电场强度的增加能隙迅速的减小，至最大外电场+0.416 VÅ-1与-0.416 VÅ-1时，能隙出现了最小值分别为0.00669 和0.00647 Hartree. 能隙的大幅度减小使得电子在分子内的大量传导变得容易［28］. 因此能够判定Au 取代二元胺DAPDI这个分子能够被有效的用作分子导线，并可通过在±X 两个方向增加外电场强度使其禁带宽度逐渐减小.

3.5 静电势

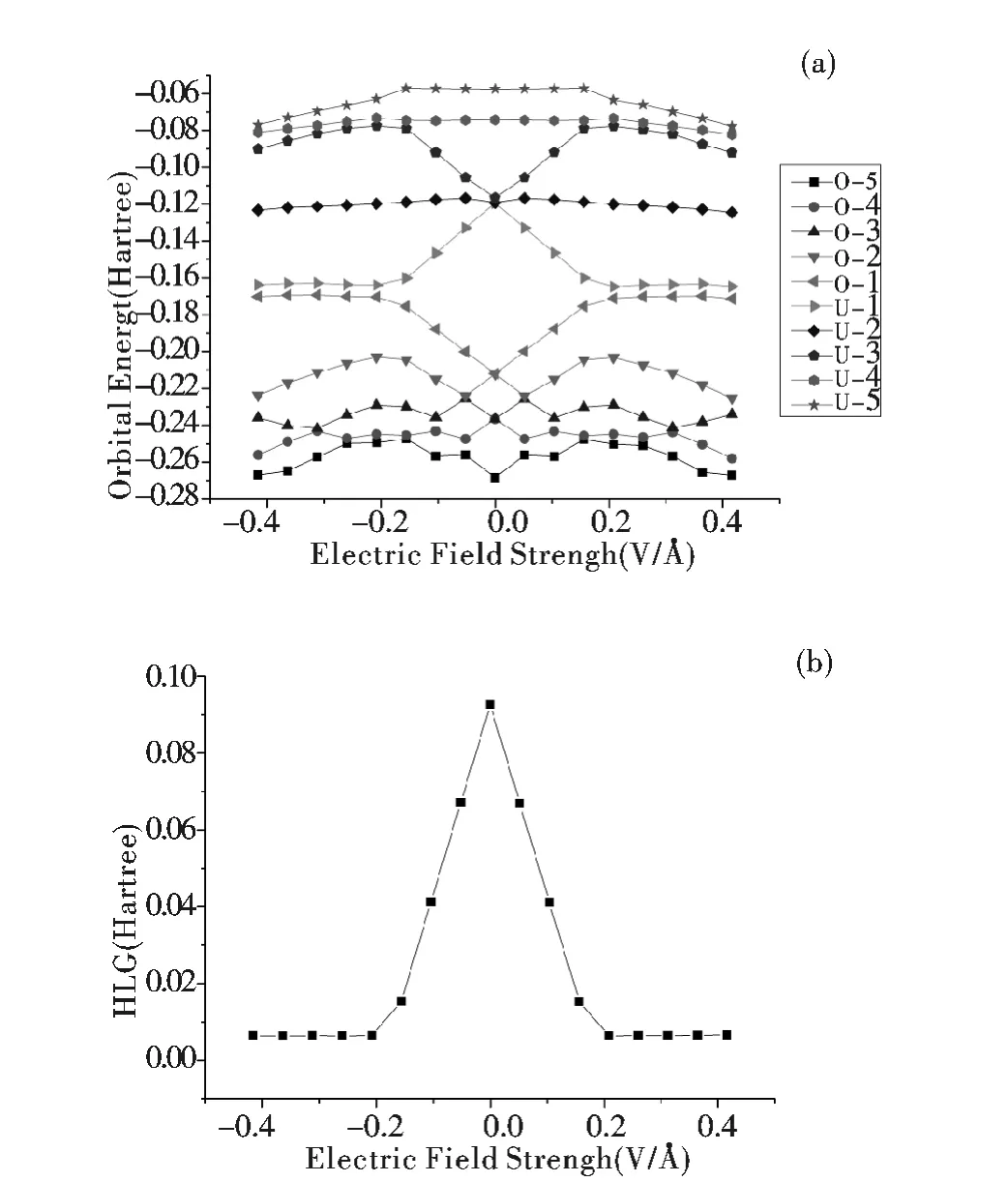
图5 不同电场强度下的占据轨道，非占据轨道，能隙的变化曲线Fig.5 Occupied MO，unoccupied MO and HLGvalues at various EF intensities

分子的静电势图像常被用来确定分子的带电区域，分析其等值面图还可以确定是电子还是原子核对带电区域做出了贡献［29，30］. 图6 是该分子导线在零电场和最大外电场时的静电势等值面图.其中蓝色表征该区域静电势为正，红色表征该区域静电势为负. 在零电场时，遍及整个分子的静电势均为正，这个正值静电势是来源于原子核的贡献. 随着外电场从零增加到最大外电场+0.416 VÅ-1，可以发现逐渐在分子的右端的Au 原子附近区域出现了高的负值静电势，同时在分子的左端仍为正值静电势，这意味着此时电子在分子内发生了迁移;同样地，当外电场反向作用时，可以发现逐渐在分子的左端Au 原子附近区域出现了高的负值静电势，同时在分子的右端仍为正值静电势. 因此，外电场方向由+X 变为-X 时，或者由-X 变为+X 时，负值静电势在分子中出现的端位会随之发生对换.

4 结 论

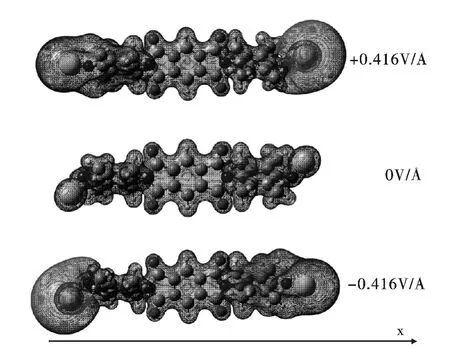
图6 零电场和最大外电场时的静电势等值面图Fig.6 Isosurface representation of ESP at the zero and the maximum applied EF intensities

采用密度泛函理论探讨了分子导线Au 取代二元胺N，N'—bis (4—amino—2，3，5，6—tetramethylphenyl)phtalene—1，2，4，5—dicarboximide(DAPDI)在不同外电场强度下的结构和电学相关性质. 计算表明该分子导线的几何结构和电子结构都对外电场敏感. 特别是在高电场强度下，电子结构受外电场的影响程度相对几何结构来说要更明显. 在场强较高时几乎所有原子的电荷变化幅度都很显著，电偶极矩会随着外电场强度的增加呈线性的增加，在高场下分子变得高度极化.当外电场在+X 或者-X 方向增强时，该分子导线的能隙会相同幅度的下降. 在最大外电场时能隙最小，此时表现出高导电性. 当外电场方向反转时，负值静电势在分子中出现的端位会随之发生对换.

［1］ Tao N J. Electron transport in molecular junctions［J］.Nature Nano，2006，1:173.

［2］ Heath J R，Ratner M A. Molecular electronics［J］.Physics Today，2003，56:43.

［3］ Joachim C，Gimzewski J K，Aviram A. A electronics using hybrid-molecular and mono-molecular devices［J］. Nature，2000，408:541.

［4］ Chiang C K，Fincher Jr C R，Park Y W，et al. Electrical conductivity in doped polyacetylene［J］. Phys.Rev. Lett.，1977，39:1098.

［5］ Aviram A，Ratner M A. Molecular rectifiers ［J］.Chem. Phys. Lett.，1974，29:277.

［6］ Reed M A，Chen J，Rawlett A M，et al. Molecular random access memory cell［J］. Appl. Phys. Lett.，2001，78:3735.

［7］ Xu B，Tao N J. Measurement of single molecule conductance by repeated formation of molecular junctions［J］. Science，2003，301:1221.

［8］ Sitha S，Bhauparkash K，Choudary B M. Electrical rectification through cumulenic bridge:a computational study［J］. Synth. Met.，2005，148:227.

［9］ Li Y，Zhao J，Yin X，et al. Ab initio investigations of the electric field dependence of the geometric and electronic structures of molecular wires ［J］. J. Phys.Chem. A，2006，110:11130.

［10］ Bijak K，Grucela-Zajac M，Janeczek H，et al. New azomethine-phthalic diimides:synthesis and thermal，optical and electrochemical charactetization ［J］.Synth. Met.，2013，175:146.

［11］ Zhao J W. Conformational analysis of 2，2-bithiophene under interaction of external electric field defined by point charges［J］. Chem. Phys. Lett.，2002，351:481.

［12］ Yin X，Li Y W，Zhang Y，et al. Theoretical analysis of geometry-correlated conductivity of molecular wire［J］. Chem. Phys. Lett.，2006，422:111.

［13］ Zhao J W. Conformational and orientational analyses of 2，2-bithiophene under interaction of external electric field constructed by point charges［J］. Synth. Met.，2002，128:261.

［14］ Frisch M J，Trucks G W，Schlegel H B，et al. Wallingford，CT:Gaussian，Inc，2009.

［15］ Dennington R，Keith T，Milliam J. Gaussview V. 5，Semichem Inc.，Shawnee Mission KS，2009.

［16］ Kumar A，Mohan C G，Mishra P C. Molecular electrostatic potential and field as descriptors of hydrogen bonding and molecular activity. Effects of hybridization displacement charge ［J］. J. Mol. Struct. THEOCHEM，1996，361:135.

［17］ Mulliken R S. Electronia population analysis on lcaomo molecular wave functions［J］. J. Chem. Phys.，1955，23:1833.

［18］ Kirtman B，Champagne B，Bishop D M. Electric field simulation of substituents in donor-acceptor polyenes:a comparison with ab initio predictions for dipole moments，polarizabilities，and hyperpolarizabilities［J］.J. Am. Chem. Soc.，2002，122:8007.

［19］ Luis J M，Duran M，Andres J L. A systematic and feasible method for computing nuclear contributions to electrical properties of polyatomic molecules［J］. J.Chem. Phys.，1997，107:1501.

［20］ Greenham N C，Friend R H，Enhrenreich H，et al.Solid state physics ［M］. San Diego，CA:Academic Press，1995.

［21］ Krohn B J，Ermler W C，Kern C W. Nuclear corrections to molecular properties［J］. J. Chem. Phys.，1974，60:22.

［22］ Pandey P K K，Santry D P. Vibrational contribution to molecular polarizabilities and hyperpolarizabilities［J］. J. Chem. Phys.，1980，73:2899.

［23］ Kern C W，Matcha R L. Nuclear corrections to electronic expectation values:zero-point vibrational effects in the water molecule［J］. J. Chem. Phys.，1968，49:2081.

［24］ Li J，Tomfohr J K，Sankey O F. Theoretical study of carotene as a molecular wire［J］. Physica E，2003，19:133.

［25］ Davis W B，Svec W A，Ratner M A，et al. Molecularwire behabiour in p-phenylenevinylene oligomers［J］.Nature，1998，396:60.

［26］ Chen J，Wang W，Reed M A，et al. Room-temperature negative differential resistance in nanoscale molecular junctions ［J］. Appl. Phys. Lett.，2000，77:1224.

［27］ Magyar R J，Tretiak S，Gao Y，et al. A joint theoretical and experimntal study of phenylene-acetylene molecular wires ［J］. Chem. Phys. Lett.，2005，401:149.

［28］ Lu J Q，Wu J，Chen H，et al. Electronic transport mechanism of a molecular electronic device:structural effects and terminal atoms［J］. Phys. Lett. A，2004，323:154.

［29］ Petrucci H R，Harwood S W，Herring F G，et al.General Chemistry:Principles and Modern Applications［M］. New Jersey:Pearson Edu. Inc.，2007.

［30］ Mishra P C，Kumar A. Molecular Electrostatic Potentials:Concepts and Applications ［M］. Amsterdam:Elsevier，1996.