ALA转子同步电机开环变频起动问题分析

皮大能，刘金华

(湖北师范学院机电与控制学院，湖北黄石435002)

0 引言

高密度轴向叠片各向异性(ALA)转子电机的定子与普通交流电机定子相同，转子由高导磁材料和非导磁绝缘材料叠片沿轴向交替高密叠压而成，具有高凸极比(Ld/Lq)［1－3］、高转矩密度、快速响应等优点，在高品质交流变速传动领域具有广阔的应用前景。但在样机实验中，发现3 相2 极ALA 转子电机在开环SPWM 变频器供电调速运行时，出现剧烈振荡和异步运行情况;在4 极ALA 转子电机的开环变频运行实验中，电机的运行情况虽有所好转，但仍然存在剧烈振荡和失步问题。因此对ALA 转子电机开环起动性能需要进一步深入探讨。

本文以2 极ALA 转子电机为例，先用小信号线性化模型分析了ALA 转子电机低频剧烈振荡产生的原因，然后把ALA 转子电机变频起动过程当作一系列不同转差率下的异步起动过程的叠加［4－6］来分析振荡后失步问题。分析结果为:剧烈振荡是在负阻尼区存在电源频率与自然频率相接近的区域，容易因扰动产生谐振;异步运行是沿q 轴方向铁芯导磁叠片中感应涡流产生的单轴转矩［7－9］导致合成转矩在S ＜0.5 时出现明显下凹甚至变负的结果。采用了最为简单经济的方法，在转子轴上附加机械惯性阻尼器增加阻尼抑制振荡。实验结果证明，理论分析思路是正确的，抑制振荡的方法是有效的。

1 振荡分析

1.1 小信号数学模型

采用小信号线性化模型分析ALA 转子电机的振荡问题。为了简化分析，假设定子线圈在气隙中产生正弦分布的磁势，忽略磁场饱和的影响和转子电流，则dq 坐标系小信号数学模型为:

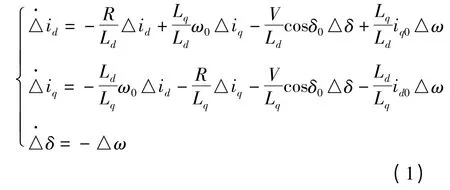
由式(1)得:

式(2)中，D、Q 分别为:

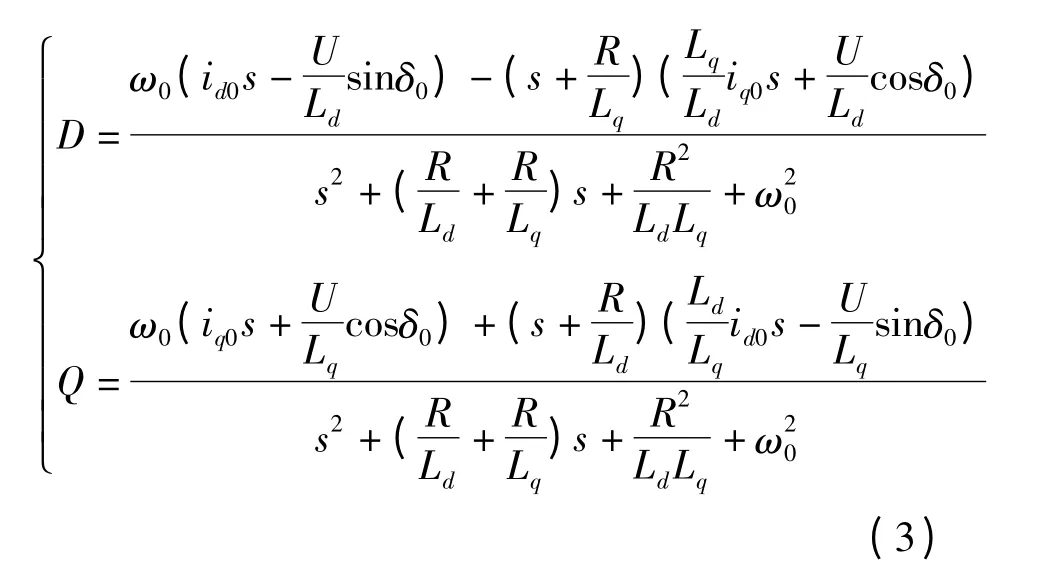
式(3)中稳态量计算:

由式(4)可求得对应某一频率和一定负载下的id0、iq0和δ0。

转矩小信号表达式:

将式(2)代入式(5)得:

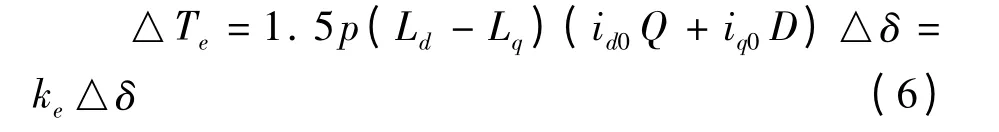
式(6)中:

ke=1.5p(Ld－Lq)(id0Q +iq0D)。

运动方程小信号表达式:

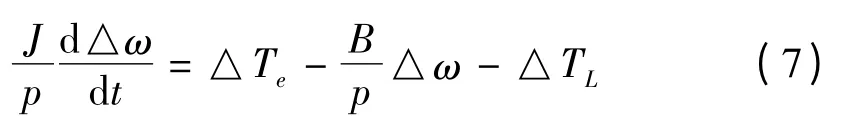
由式(7)得负载小扰动动态模型框图如图1所示。

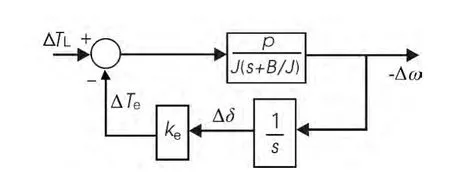
图1 小信号动态模型框图

图1 的传递函数为:

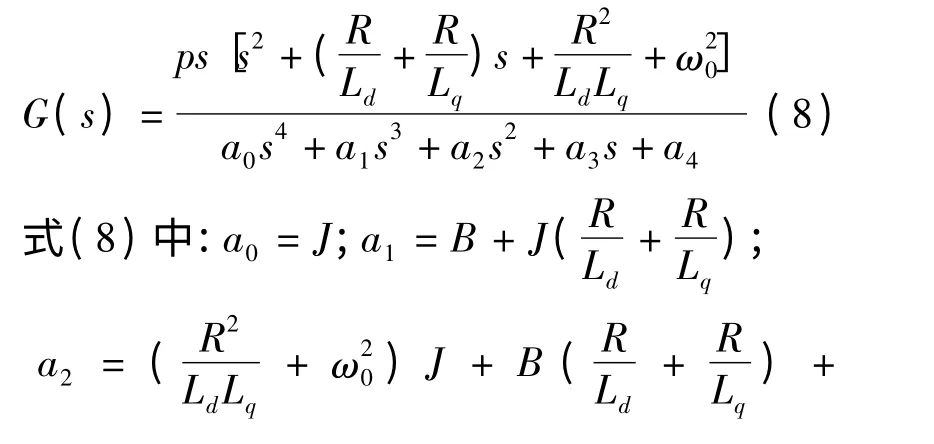
由线性系统理论可知，若G(s)对应某一工作频率的所有特征值的实部均为负值，则系统在该频率和所给定的运行条件下是稳定的，否则为不稳定［10］。

1.2 算例及分析

实验样机主要参数:电源相电压UN=220 V，P =1，定子电阻r1= 2.5 Ω，转子转动惯量J =0.010 3 kg·m2，频率为50 Hz，定子漏感L1σ=0.013 1 H，d 轴电枢反应电感Lad=0.366 9 H，q 轴电枢反应电感Laq= 0.038 3 H，rdr=0.44 Ω，rqr=380.3 Ω，L2σd=0.005 2 Ω，L2σq=0.004 12 Ω。

在Matlab 环境中，计算的不同频率主导特征值轨迹如图2所示，对应的阻尼系数ζ 与电源频率f 的关系如图3所示。对照图2 及图3发现，电源频率约超过12 Hz 进入了不稳定区，在此区对应的阻尼系数ζ 为负值。不同频率变频起动时转矩与转差率曲线如图4所示。在电机开环变频起动过程中，电源频率上升到12 ～18 Hz 不稳定区最容易因扰动发生谐振，也就出现了振荡现象。图4 中虽然在约22 Hz负ζ 时绝对值最大，但振荡反而减缓，因为其不在谐振区。

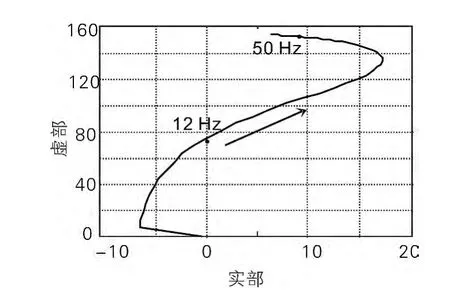
图2 不同频率的主导特征值轨迹

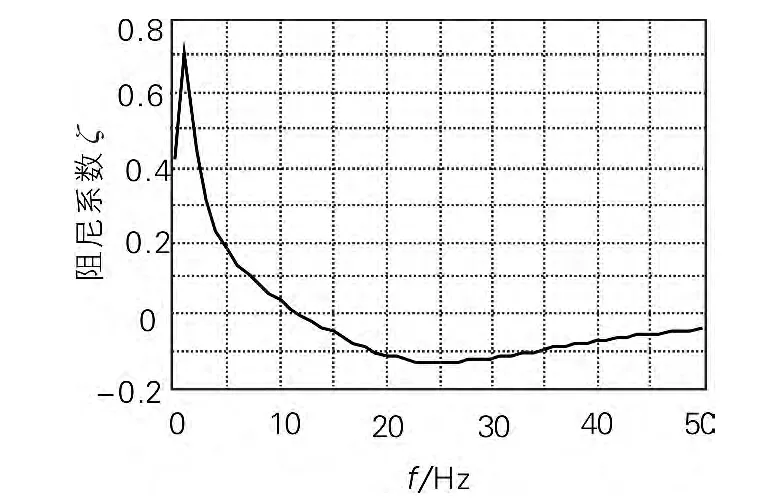
图3 阻尼系数ζ 与电源频率f 的关系

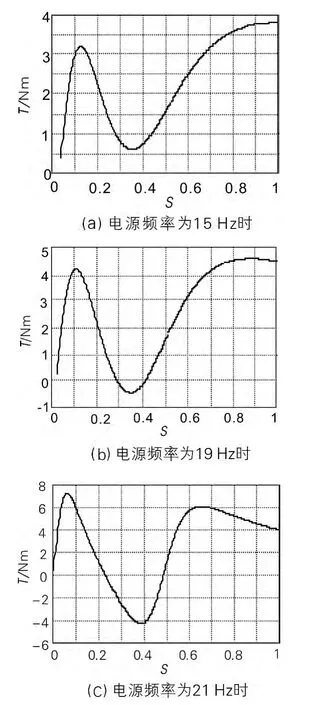
图4 不同频率变频起动时转矩与转差率曲线

2 异步运行分析

2.1 数学模型

把ALA 转子电机变频起动过程当作一系列不同转差率下的异步起动过程的叠加，不忽略转子电流时，异步运行的数学模型为:

式(9)中:S 为转差率，ψd、ψq、ψdr和ψqr分别为:

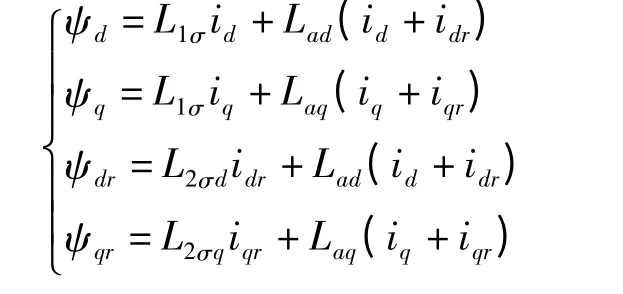
采用运算电抗求解式(9)中的d、q 轴磁链和电流为:

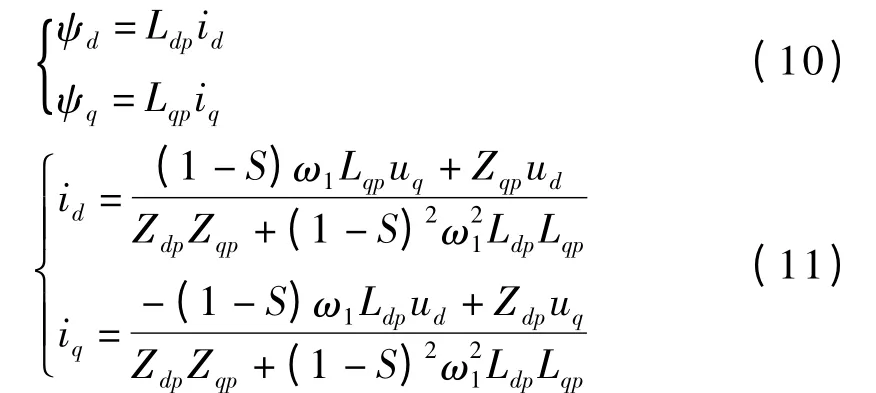
式(10)中运算电感和阻抗分别为:

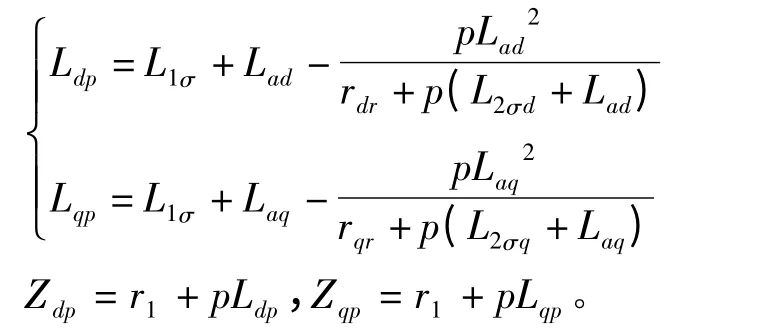
将p =jSω1代入式(10)和(11)得:

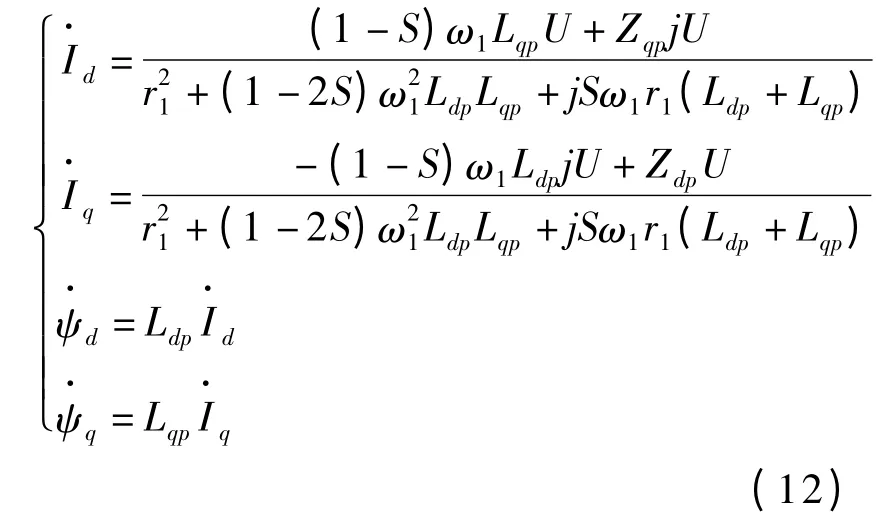
转矩表达式为:

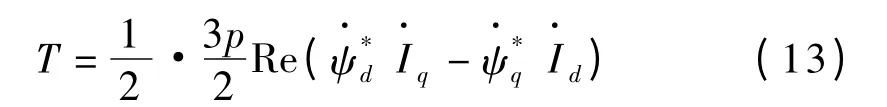
将式(12)代入式(13)得T = f(S)函数，编写计算程序，可得T = f(S)曲线如图4所示。

2.2 计算结果及分析

从图4 中可见，ALA 转子电机d、q 轴合成转矩特性曲线在S ＜0.5 时发生明显下凹，而且当电源频率大于18Hz 时下凹区变负(图4(b)和图4(c))，频率越大，负值区域越宽。主要原因是转子无起动绕组，沿q 轴方向铁芯导磁叠片中感应涡流产生了单轴转矩。当电机发生剧烈振荡，可能进入下凹区的最低点(图4(a))或负值区(图4(b)和图4(c))，此时电磁转矩小于空载转矩，电机减速运行，直至异步转矩等于空载转矩达新的平衡点(转差率略低于0.5)，磁阻转矩则以平衡转速点为中心脉振交变。由此可见，ALA 电机由于转子结构的特殊性，在S＜0.5 时转矩明显下凹甚至变负是接近半同步速异步运行的主要原因。由图4(c)可知直接接工频电源起动，在异步转矩的作用下，电机从0 开始加速，到接近半同步速处，起动转矩与空载转矩平衡，电机在平衡点处振荡运行，直接起动时的转速及电流曲线如图5所示，理论分析与图5 实验结果相符。

图5 直接起动时的转速及电流曲线

3 实验

从以上分析可知，ALA 转子电机发生剧烈振荡是在负阻尼区变频电源频率与自然频率相接近因扰动产生了谐振，增大电机的阻尼使ζ ＞0，电机不发生振荡或轻微振荡，起动过程可能不进入转矩的下凹区;在开环逆变器电源起动下，电机依靠磁阻转矩能牵入同步，因此改善电机起动性能的首要任务是抑制振荡，而最为经济简单的方法是在转子轴上直接附加合适的机械惯性阻尼器，增大转子阻尼，消耗转子振荡能量，减小振荡幅度。机械惯性阻尼器的工作原理见文献［11］。加机械惯性阻尼器后的转速实验波形如图6所示。

图6 加机械惯性阻尼器后的转速实验波形

为了验证分析的正确性，在实验系统中，使用同样的电机和通用变频器供电，开环V/f控制，SPWM 调制波，在转子轴上直接附加机械惯性阻尼器，变频器具有起/停和加/减速功能，起动过程中，电源频率按设定斜率从零逐渐增加到预定值。表1 是2 极ALA 转子样机的变频空载起动实验数据。附加惯性阻尼器后电流变化趋缓，转速波动幅值减小，电机能达到同步运行速度。

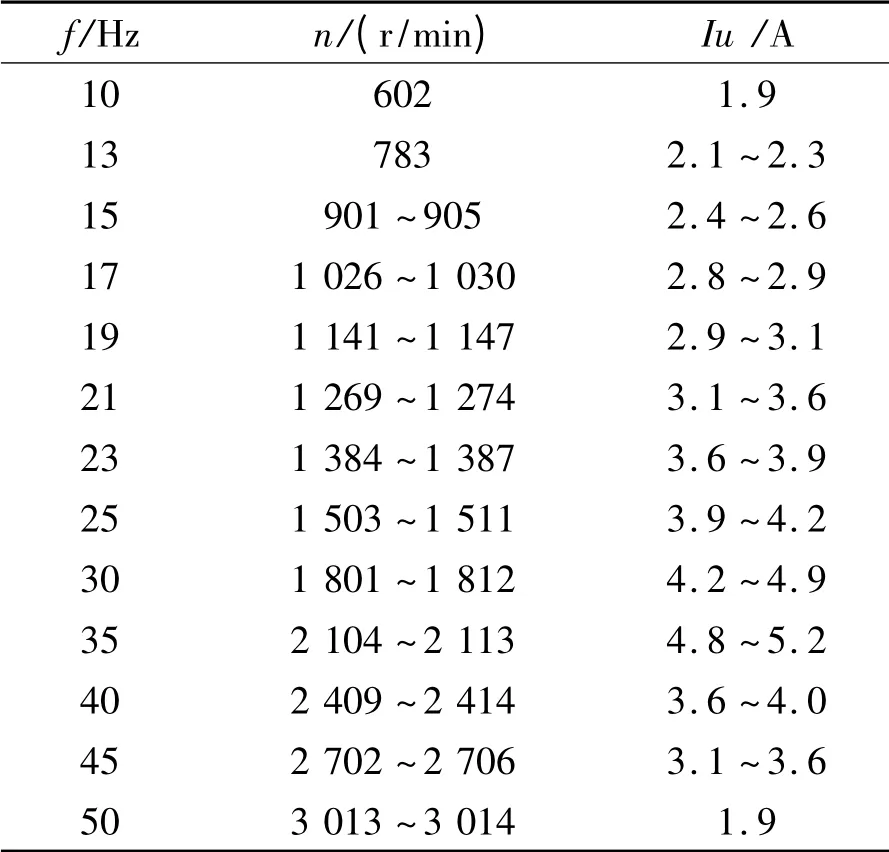
表1 样机逆变器电源空载起动数据

4 结论

ALA 转子电机剧烈振荡的主要原因是出现了负阻尼，而且在负阻尼区存在电源频率与自然频率相接近的区域，容易因扰动产生谐振;异步运行的主要原因是q 轴方向的铁芯导磁叠片中感应涡流产生的单轴转矩使合成转矩在S ＜0.5 时出现明显下凹甚至变负，电机振荡失步后进入下凹区，减速运行直到新的平衡点。采取了在转子轴上直接附加机械惯性阻尼器抑制振荡的方法，实验结果表明此方法是有效的，也进一步证明了该分析方法是正确的。

［1］Nicola Bianchi，Chalmers Brian J.Axially laminated reluctance motor:analytical and finite－element methods for magnetic analysis［J］.IEEE Transactions on Magnetics，2002，38(1):239－245.

［2］Arkadan A A，Isaac F N，Mohammed O A.Parameters evaluation of ALA synchronous reluctance motor drives［J］.IEEE Transactions on Magnetics，2000，36(4):1950－1953.

［3］陈学珍.新型ALA +SPM 组合式转子电机设计及实验研究［D］.武汉:华中科技大学，2011.

［4］叶东，张锋奇，孙丽玲，等.稀土永磁同步电动机起动过程研究［J］.中国电机工程学报，1998，18(5):335－339.

［5］熊浩，孟光伟，向东，等.单相永磁同步电动机变频起动性能分析［J］.微特电机，2009，37(3):23－24.

［6］Mircea Popescu，T J E Miller，Malcolm I McGilp，et al.Line－start permanent－magnet motor:single－phase starting performance analysis［J］.IEEE Transaction on Industry Applications，2003，39(4):1021－1030.

［7］辜承林，易明军.轴向迭片各向异性转子电机振荡及异步运行分析［J］.中国电机工程学报，2000，20(12):7－10，88.

［8］易明军，辜承林.ALA 转子电机的实验研究［J］.微特电机，2000，28(6):6－9.

［9］吴志桥.ALA 转子新结构及其实验研究［D］.武汉:华中科技大学，2002.

［10］陈学珍，辜承林.组合转子同步电机稳定性探讨［J］.电机与控制学报，2010，14(12):41－46.

［11］朱建华，辜承林.变频器驱动下ALA 转子电机运行性能的实验研究［J］.微特电机，2007，35(7):1－3，7.