多股进料搅拌釜停留时间分布的信息熵

王宇良，郑海俊，周业丰，黄正梁，王靖岱，阳永荣

（浙江大学 化学工程联合国家重点实验室，化学工程与生物工程学系，浙江 杭州310027）

目前关于不同装置内流动与混合情况的研究多是针对单股进料和单股出料系统，然而实际化学反应器、混合器、燃烧室和精馏塔等常具有多股进料或多股出料［1］.此外，生理系统［2］以及湿地的水流汇合和分流过程［3］中也存在类似情况.

对于具有多股进料或出料的系统，装置内的混合质量尤为重要.以具有多股进料的高压聚乙烯釜式反应器为例，如果混合不良，局部引发剂浓度过高会导致产品质量下降，严重时甚至发生爆聚，造成停车.该反应器长径比很大，内部结构复杂，并且目前缺乏对其中流体流动、混合情况的充分认识，这都限制了反应器的优化与放大.因此，对具有多股进料或出料的复杂系统的内部流动混合情况进行研究具有重要的实际意义.

停留时间分布可以描述系统内的流动特性，是微观混合过程在宏观上的表现.Nauman［4］综述了停留时间理论的发展历程、相关研究成果以及在不同领域的应用情况，认为停留时间理论虽然成熟但是并非停滞不前.Leclerc等［5］扩展了停留时间分布理论，通过由基本反应器相互连接的复杂网络来理解停留时间分布，并开发了软件包.该软件可以用于模型的选择和模型参数的检验，多股进料和出料过程可以通过卷积和最优化进行模拟.

停留时间分布常采用示踪响应法进行测定，由实验数据处理得到停留时间分布密度函数E（t）.为了比较不同条件下测得的停留时间分布，通常是比较其统计特征值，如数学期望、方差.将这些特征值代入多釜串联模型和轴向混合模型求取模型参数，以此反映流体的流动混合情况.但是，这些模型都是根据单股进料和单股出料的系统推导得出，应用于具有多股进料或出料的系统时存在困难.具有多股进料或出料的装置，往往具有复杂的结构，不同的进料口与出料口的组合，得到的停留时间分布可能存在巨大差异.在某些组合下，可能导致装置内流体存在滞留区，由停留时间分布曲线得到的无因次方差甚至会大于1［4］.可见，将传统的方差分析应用于多股进料或出料的系统时，可能得到片面甚至错误的结论.

信息熵（information entropy）可以用于描述混合效果，因为大多数的混合现象都可以利用概率进行解释.信息熵由信息论之父Shannon［6］于1948年首次提出，故又称Shannon熵（香农熵）.信息熵是信息源紊乱程度的量度，反映系统运动状态的随机性.近年来，不少研究者将信息熵概念应用到物理、化学、生物及工程等领域中，取得了丰硕的成果［7-15］.

在化学工程领域，信息熵已经被成功应用于鼓泡塔、流化床和气力输送等过程的复杂流动信号的分析，表明信息熵能较好地反映流体的流动特征.Manish等［11］采用信息熵理论分析了下流式鼓泡塔的示踪剂浓度变化数据，以一个无因次参数描述装置内混合情况，并将该参数与传质效率进行关联.Gui等［12］采用离散元耦合大涡模拟方法（discrete element method-large eddy simulation，DEMLES）对鼓泡流化床进行计算流体力学（computational fluid dynamics，CFD）模拟，并对颗粒的交叉径向分布函数进行信息熵分析，研究发现平均信息熵可以很好地表征不同操作条件下的宏观混合情况.Nedeltchev等［13］基于信息熵理论和信号划分区域分析，提出了多相流反应器（鼓泡塔，流化床，喷射床）中不同流型辨识的新方法.Rakoczy等［14］通过停留时间分布实验研究了旋转磁场内一种混合器的混合特征，采用信息熵理论对停留时间分布数据进行处理，提出信息混合能力的概念用于描述在旋转磁场下的连续流动系统的混合质量.钟文琪等［15］基于压力脉动信号的信息熵分析，建立了信息熵与喷动流化床中流型之间的联系.

本文针对多股进料复杂流动系统，以搅拌釜为例，采用脉冲示踪实验，考察不同示踪剂进料位置和不同操作条件下的停留时间分布，并结合信息熵理论方法对数据进行处理与分析，提出信息熵混合度的概念用于表征流动与混合情况，以期揭示搅拌釜装置内的流动特性.此外，通过实验方法验证多股进料条件下总停留时间分布的叠加规则.

1 实验装置及方法

1.1 实验装置

实验装置如图1所示.采用高为2 150 mm、内径为210 mm的有机玻璃搅拌槽作为冷模实验装置，该装置有4个进料口，1个底部出料口，装置相关参数见表1.表1中，di为筒体内径，ds为搅拌轴直径；h为筒体高度；hb为中部轴承套高度；h1、h2、h3及h4为4个进料口（下文中以inlet1、inlet2、intel3及inlet4表示）的高度.搅拌轴上共装有32层搅拌桨，其中29层为直径190 mm的双叶斜桨，桨面与运动方向的倾斜角为10°.此外在装置顶部与中部分别装有直叶涡轮，装置底部安装一个类似锚式的特殊桨.在中部直叶涡轮上方有一轴承套，其中轴承起到固定搅拌轴的作用，轴承套和搅拌轴的截面积占据了装置截面积的75%左右.

图1 具有4股进料和单股出料搅拌釜的停留时间分布实验示意图Fig.1 Schematic diagram of RTD experiments in stirred tank with four inlets and one outlet

表1 搅拌釜实验装置参数Tab.1 Parameters of experimental apparatus of stirred tank mm__

采用自来水作为实验介质，搅拌转速n通过变频器进行控制.装置内液面高度为2.0 m，液体体积为67.0 L.工业装置在稳定运行时，inlet1的流量为其他进料口的一半，故取inlet1流量为0.5 m3／h，取inlet2、inlet3及inlet4流量为1.0 m3／h.

实验以饱和KCl溶液作为示踪剂，采用脉冲法测量停留时间t分布，使用电导率仪测定装置出口处液体的电导率.t=0时，通过进料口旁的支路以注射器脉冲注入40 mL示踪剂，同时开始记录出口处的电导率c（t）.实验所用自来水的电导率约为170μs／cm，为了消除自来水电导率对实验结果的影响，对c（t）进行归一化处理，得到无因次的电导率c′（t）：

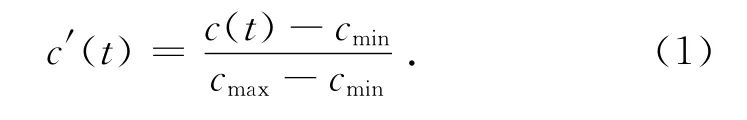
式中：cmin、cmax分别为单次实验过程中电导率的最小值与最大值.由c′（t）可以计算得到相应的停留时间分布密度函数：

1.2 分析方法

1.2.1 方差分析 采用方差分析［16］求E（t）的数学期望，得到平均停留时间

求E（t）对¯t的二次矩，可得方差

为了便于比较不同条件下的停留时间分布，定义无因次时间θ：

则无因次停留时间分布密度函数E（θ）：

已知对于平推流有

1.2.2 信息熵分析 通常，一个随机变量的信息熵根据其概率分布定义.设X是一个离散的随机变量，共有N种取值，其取值为χi（i=1，2，…，N）的概率p i=p（χi），则有

χi事件所对应的自信息量定义为式中：对数底a通常取2、e或10，对应信息熵的单位分别为bit、nat、det，三者可以互相换算.下文的推导中会涉及e，故本研究的信息熵中对数底均取e.

信息熵H定义为信源的加权平均信息量，即

规定当p（χi）=0时，-p（χi）loga p（χi）=0.确定概率事件的信息熵最小，完全随机事件的信息熵最大.

概率密度为p（χ）的连续随机变量有

或

式中：Δt为时间步长.

在进行停留时间分布实验时，出口处示踪剂浓度降到0的时刻为tm，则式（16）中N≥m，m表示离散随机变量，有m种取值.

将信息熵理论应用于停留时间分布的分析是基于示踪剂到达出口所需时间的不确定性.为了便于比较，可对信息熵进行归一化处理［14，17］，定义一个无因次参数M——信息熵混合度，用以表示流动情况接近平推流或者全混流的程度：

式中：Hmin为信息熵的最小值，Hmax为信息熵的最大值.对于平推流，将式（9）代入式（15），可得

对于全混流，将式（10）代入式（15）可得

对于m个进料口、单个出料口的闭式系统，应用全混流模型，可知

式中：V为装置容积，q为进料总体积，等于各股进料流量之和.

将式（16）、（18）～（20）代入式（17），可得对于多股进料、单股出料的闭式系统，信息熵混合度为

式中：M为以信息熵表示的混合程度.数值介于0～1.0，其中0表示平推流，1.0表示全混流.显然，M越大，则E（t）越接近于全混流状态，混合质量越好.

2 结果与讨论

当装置有多股进料时，不但要掌握总停留时间分布，还要掌握各个进料口对应的停留时间分布.后者往往对装置的设计与优化具有重要的指导意义.

2.1 4股进料单股示踪时停留时间分布的方差分析

为了研究不同位置进料所对应的停留时间分布，保持进口1、进口2、进口3和进口4的流量不变，只在其中一个进料口处脉冲注入饱和KCl溶液作为示踪剂.实验考察了示踪剂进料位置（进口1～进口4）、搅拌转速n（300～700 r／min）对停留时间分布的影响，结果如图2所示.

根据1.2.1节的方差分析方法，求得平均停留时间与无因次方差σ2θ，结果如表2所示.

表2 不同搅拌转速和示踪剂进料位置下的平均停留时间与无因次方差___Tab.2 Influences of agitation speed and tracer inlet position on mean residence time and dimensionless variance___

由表2可以发现，从进口1到进口4，越靠近装置出口，则平均停留时间越短，说明示踪剂在轴向的返混较小.尤其对进口4，其平均停留时间远低于其他示踪剂进料点，说明示踪剂主要分布在装置下部，装置上部相当于滞留区，示踪剂未能在整个装置内实现良好混合.然而从进口1到进口4，无因次方差却逐渐增大，表示越接近全混流状态，显然这与实际情况矛盾.由此可见，无因次方差并不适用于这类多股进料条件下的停留时间分布数据的分析，不能很好地反映不同进料位置、不同操作条件下的混合情况.下面将采用信息熵的方法来对停留时间分布数据进行处理和分析.

图2 不同搅拌转速和示踪剂进料位置下的停留时间分布实验结果Fig.2 RTD experimental results under different agitation speeds and tracer inlet positions

2.2 4股进料单股示踪时停留时间分布的信息熵分析

M与搅拌雷诺数及示踪剂进料位置的关系如图3所示.从图3可以发现，M与搅拌雷诺数Re及示踪剂进料位置都有密切关系，但是两者的影响效果有所不同.相同的示踪剂进料位置下，随着Re增大，液体湍流程度加强，示踪剂在装置内分布更加均匀，M随之增大.在相同的搅拌雷诺数下，示踪剂进料位置离装置出口越远，则示踪剂在整个装置内的分布越均匀，M越大.示踪剂进料位置为进口1与进口2的M很接近，这是由于进口1与进口2均位于装置顶部，与出料口之间的距离很接近，如图1所示.

图3 搅拌雷诺数和示踪剂进料位置对信息熵混合度的影响Fig.3 Influences of Reynolds number and tracer inlet position on M

图3中进口4的M值远小于其他进料点，造成这种差异主要有2方面原因.一方面，装置出料口位于底部，且进料、出料流量不变，则液体流动的平均速度一定且方向往下，导致位于装置顶部的进口1～进口2注入的示踪剂的平均停留时间较长.而进口4距离装置出口较近，平均停留时间较短.另一方面，装置中部的轴承套和搅拌轴的截面积占据了装置截面积的75%左右，轴承套起到分区挡板的作用，因此在进口4注入的示踪剂难以返混至装置上部区域，上部区域相当于滞留区.总之，进口1和进口2中注入的示踪剂可以随主体流动通过轴承套与装置内壁的间隙进入下部区域，在整个装置内实现较均匀的分散.进口4注入的示踪剂主要停留在下部区域，较快地离开装置，难以到达装置上部区域.

此外，存在一个有趣的现象：当Re较小时，进口3的M明显小于进口2的M；而当Re足够大时，两者的M值非常接近.搅拌槽内存在3种扩散作用：主体对流、漩涡扩散以及分子扩散.inlet3位于装置中部位置，且装置内液体流动的平均速度往下.因此，搅拌雷诺数较小时，流体湍动程度较低，示踪剂主要随主体流动往下扩散，较快地进入下部区域，未能在上部区域充分扩散.示踪剂在整个装置内分布不够均匀，因此M较小.而当搅拌雷诺数增大时，3种扩散作用均有所增强，轴向返混加剧，示踪剂能同时在上下两区域实现较好地扩散.

对比方差分析和信息熵分析的结果可知，对于多股进料的复杂流动系统，停留时间分布的无因次方差并不能准确地反映装置内的流动与混合情况，在某些情况下甚至得到错误的结论.而信息熵混合度M可以准确反映流体的流动与混合特性.这是因为无因次方差的计算需要已知平均停留时间，而由停留时间分布数据计算得到的平均停留时间与装置的结构、进出料的情况相关，往往偏离理论值（V／q）.由此得到的无因次方差只能反映该曲线的性质而不能准确反映流动与混合的情况.而式（17）明确了M的意义为停留时间分布曲线的信息熵H接近全混流Hmax或平推流Hmin的程度.由M值的大小可以初步判断流体的混合程度：M值越接近于1，则越接近全混流；M值越接近于0，则越接近平推流.

2.3 总停留时间分布的方差分析和信息熵分析

通过实验可测得总停留时间分布，方法如下：在t=0时刻，进口1～进口4同时脉冲注入示踪剂（10～20 m L），同时记录装置出口处液体的电导率变化.由于inlet1流量为其他进料口的1／2，为了保持各进料口示踪剂脉冲浓度一致，inlet1加入的示踪剂体积为其他进料口的1／2.实验结果如图4所示.对数据分别进行方差分析和信息熵分析，结果如表3所示.

从图4可以看出，随着搅拌转速增大，停留时间分布曲线的峰变窄，拖尾现象加剧.由表3可知，随着搅拌转速的增大，由方差分析得到，平均停留时间与无因次方差均呈增大的趋势，由信息熵分析得到的M值也呈增大的趋势.

图4 不同搅拌转速下的总停留时间分布实验结果Fig.4 Overall RTD experimental results under different agitation speeds

搅拌转速增大，则搅拌雷诺数Re随之增大，装置内流体的湍流程度加强，返混更加剧烈，混合更加接近于全混流，所以平均停留时间增大，无因次方差增大.同样，E（t）紊乱程度增大，M呈增大的趋势，更趋近于1.

实验装置搅拌器共安装多层搅拌桨，层间距低于搅拌桨直径.旋转搅拌桨能同时产生径向流和轴向流，混合效率较高.且实验条件下Re＞180 000，液体处于完全湍流状态［18］.多股注入的示踪剂能快速均匀地分散到整个装置内.这与全混流的情况相似，故认为其接近于全混流.而由表3的计算结果可知，信息熵分析得到的M接近于1，说明搅拌釜接近于全混流，信息熵分析结果与实际情况相符合.

综上所述，信息熵理论可应用于停留时间分布的分析，对于多股进料的复杂流动系统，与无因次方差相比，M能够更加准确地反映流体的流动与混合特性.在比较不同进料口的流体在整个装置中的流动与混合情况时，M值的优势更加明显.

2.4 总停留时间分布叠加规则的信息熵验证

针对多股进料和出料的复杂流动系统，不少研究者通过理论推导与实验方法得到总停留时间分布的叠加规则.Buffham等［19］最早对此进行研究，认为具有多股进料和出料系统的总停留时间分布密度函数遵守如下叠加规则：

式中：q是总体积流量，qej是第j股出料的流量，E kj是第j个出料口因第k个进料口注入的示踪剂所产生的停留时间分布密度函数.Ritchie等［20］提出了不同的叠加规则：

式中：qkj是第k个进料口的进料中从第j个出料口流出的流量

庄震万［1］采用多釜串联模型，通过理论推导，建立了多股进料多股出料系统在理想、非理想流动情况下的总停留时间分布的叠加规则，结果与式（22）相同.对于本研究中的4股进料单股出料系统，根据式（22）或（23）均可得到相同的总停留时间分布叠加规则：

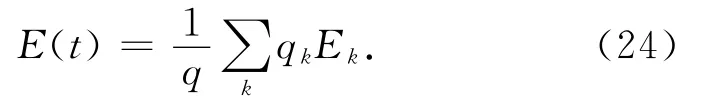
式中：Ek为第k个进料口注入的示踪剂所对应的停留时间分布.

对图2的实验数据按式（24）进行处理，得到总停留时间ts分布的计算值.实验测得的总停留时间分布曲线如图4所示.将计算值与实验值进行对比，典型曲线如图5所示.分别计算实验值与计算值的信息熵混合度，结果见表4.

图5 不同搅拌转速下总停留时间分布计算值与实验值的对比Fig.5 Comparison of calculated values with experimental data of overall RTD under different agitation speed

表4 总停留时间分布的信息熵混合度Tab.4 Information entropy mixing degree of overall RTD

从图5及表4可以发现，按叠加规则计算得到的总停留时间分布与实验值吻合良好.通过信息熵分析可知，信息熵混合度的计算值（Mcal）与实验值（Mexp）的相对偏差δ在2%以内，验证了叠加规则式（18）的正确性.Mexp略小于Mcal，这是由于实验的系统误差，4个进料口处的示踪剂脉冲并非完全相同，且脉冲进入装置内的时间有所差别.inlet1示踪剂注入点到装置的距离较远，故实验时产生的峰延后.从图5可以发现，实验的E（t）峰值低于计算值；峰值过后，随着t增大，两者差距不断缩小，直到实验的E（t）超过计算值.可见，与计算值相比，实验的E（t）分布较均匀，则信息熵较小，这与方差分析类似.

实验和计算得到的M值均大于0.95，说明在整个装置内流体流动情况接近于全混流；在实验所采用的搅拌雷诺数范围内，流体处于完全湍流状态；随着搅拌雷诺数增大，流体混合效果增强，M值有所增大.

3 结 论

（1）对于多股进料的复杂流动系统，与无因次方差相比，M能够更加准确地反映流体的流动与混合特性.M介于0～1.0，其中0代表平推流，1.0代表全混流.

（2）M随着搅拌雷诺数的增大而增大，随示踪剂进料位置与装置出口距离的降低而减小.装置中部的轴承套起到分区挡板的作用，上部分区物料容易进入下部分区，但下部分区物料难以返混至上部分区.

（3）对实验测得的总停留时间分布和由叠加规则计算得到的总停留时间分布分别进行信息熵分析，验证了叠加规则的正确性.M值均大于0.95，说明装置内整体混合情况良好，接近于全混流.

（

）:

［1］庄震万.具有多股进料和出料的系统的流动模型［J］.中国科学：A 辑，1980，10：12.ZHUANG Zhen-wan.Flow model of equipment with multiply inlets and oulets［J］.Science in China：Series A，1980，10：12.

［2］江晖.氨苄西林与舒巴坦匹酯经口服在肉鸡体内的药物动力学及组织分布研究［D］.武汉：.华中农业大学，2012：7- 20.JIANG Hui.Pharmacokinetics and tissue distribution of ampicillin and sulbactam pivoxyl following oral administration in chickens［D］.Wuhan：Huazhong Agricultural University，2012：7- 20.

［3］WANG H，JAWITZ J W.Hydraulic analysis of cellnetwork treatment wetlands［J］.Journal of Hydrology，2006，330（3／4）：721- 734.

［4］NAUMAN E B.Residence time theory［J］.Industrial and Engineering Chemistry Research，2008，47（10）：3752- 3766.

［5］LECLERC J P，CLAUDEL S，LINTZ H G，et al.Theoretical interpretation of residence-time distribution measurements in industrial processes［J］.Oil and Gas Science and Technology，2000，55（2）：159- 169.

［6］SHANNON C E，A mathematical theory of communication ［J］.Bell System Technical Journal，1948（27）：379- 423，623- 656.

［7］CHATZISAVVAS K C，MOUSTAKIDIS C C，PANOS C P.Information entropy，information distances，and complexity in atoms［J］.Journal of Chemical Physics，2005，123（17）：174111.

［8］STAHURA F L，GODDEN J W，XUE L，et al.Distin-guishing between natural products and synthetic molecules by descriptor Shannon entropy analysis and binary QSAR calculations［J］.Journal of Chemical Information and Computer Sciences，2000，40（5）：1245- 1252.

［9］STRAIT B J，DEWEY T G.The Shannon information entropy of protein sequences［J］.Biophysical Journal，1996，71（1）：148- 155.

［10］LI H，BAO Y Q，OU J P.Structural damage identification based on integration of information fusion and shannon entropy［J］.Mechanical Systems and Signal Processing，2008，22（6）：1427- 1440.

［11］MANISH P，MAJUMDER S K.Quality of mixing in a downflow bubble column based on information entropy theory［J］.Chemical Engineering Science，2009，64（8）：1798- 1805.

［12］GUI N，FAN J.Numerical study of particle mixing in bubbling fluidized beds based on fractal and entropy analysis［J］.Chemical Engineering Science，2011，66（12）：2788- 2797.

［13］NEDELTCHEV S，SHAIKH A.A new method for identification of the main transition velocities in multiphase reactors based on information entropy theory［J］.Chemical Engineering Science，2013，100：2- 14.

［14］RAKOCZY R L，KORDAS M，STORY G，et al.The characterization of the residence time distribution in a magnetic mixer by means of the information entropy［J］.Chemical Engineering Science，2013，105：191- 197.

［15］钟文琪，章名耀.基于信息熵分析的喷动流化床流动特性［J］.化工学报，2005，56（12）：2303- 2308.ZHONG Wen-qi，ZHANG Ming-yao.Flow characteristics in spou-t fluid bed by Shannon entropy analysis［J］.Journal of Chemical Industry and Engineering，2005，56（12）：2303- 2308.

［16］陈甘棠.化学反应工程［M］.北京：化学工业出版社，2007：88- 109.

［17］NEDELTCHEV S，OOKAWARA S，OGAWA K.A fundamental approach to bubble column scale-up based on quality of mixedness［J］.Journal of Chemical Engineering of Japan，1999，32（4）：431- 439.

［18］王凯，虞军.化工设备设计全书：搅拌设备［M］.北京：化学工业出版社，2003：17- 31.

［19］BUFFHAM B A，KROPHOLLER H W.The washout curve，residence-time distribution，andFcurve in tracer kinetics［J］.Mathematical Biosciences，1970，6：179- 184.

［20］RITCHIE B W，TOBGY A H.Residence time analysis in systems having many connections with their environment［J］.Industrial and Engineering Chemistry Fundamentals，1978，17（4）：287- 291.