脉冲TEA CO2激光器输出模拟

胡 志，王又青，刘 顺，卢丽娟，李 波

(华中科技大学光学与电子信息学院激光加工国家工程研究中心，武汉430074)

引 言

脉冲横向激励大气压(transversely excited atmospheric，TEA)CO2激光器中存在着 CO2，N2，He 以及由CO2分解出来的CO，各种气体的碰撞激发和弛豫过程相当复杂，激光输出功率与各种碰撞和弛豫密切相关。目前已经有多种方法被用来研究CO2激光器的动态特性和输出参量。其中包括RUDOLPH和HARENDT等人针对CO2激光器的不同激励方式给出了不同的电子密度方程［1］。SMITH和THOMSON将振动模式作为简谐振子的六温度模型［2］。华中科技大学LU和WANG等人研究了双波长可调谐TEA CO2激光器的脉冲输出特性［3］。中国科学院电子研究所 DING和WAN研究了脉冲CO2激光器的多频动力学模型［4］。然而关于脉冲TEA CO2激光器输出与激光器工作气体配比、抽运电子密度、激光器腔长的关系还不明确。本文中将在六温度模型的基础上，结合激光器内光强与输出功率的控制方程，对脉冲TEA CO2激光器进行理论分析和数值模拟，并与实验对比，验证所得结论。

1 理论模型

1．1 模型假设和CO2激光器的能级原理图

六温度模型由1组描述CO2，N2和CO分子振动能级密度随时间变化的非线性微分方程组成。该模型比较全面地反映了激光器工作气体中不同分子振动模式间的能量转移过程［5-7］。模型运用在以下假设条件下:(1)每个振动模式由其玻尔兹曼平衡温度来表示;(2)受激辐射只发生在10P(20)谱线，即(0001，19)→(1000，20)能级之间(10.6μm);(3)在谐振腔内沿着气体流体方向，气体压强作为常量，没有损耗;(4)考虑CO2分子的分解影响，本文中假设为某个分解比例;(5)各能级的弛豫时间与混合气体种类、气体温度以及气体压强有关。

CO2激光器中不同分子的能级原理图如图1所示。图中Xi(i=1，2，…，5)表示不同的电子抽运激励速率，En(n=1，2，…，5)表示不同能级，τi和 τij表示不同的弛豫速率，V为0或1是指CO或N2的不同振动模式，而Vj(j=1，2，3)表示CO2的不同振动模式。

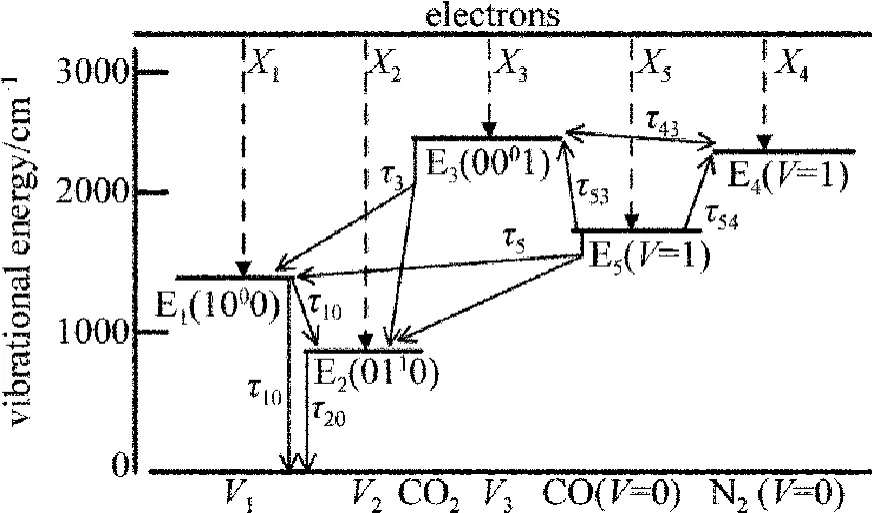
Fig.1 Schematic diagram of different energy levels of CO2laser

1．2 六温度模型

E1，E2，E3分别为单位体积CO2分子的对称振动模式、弯曲振动模式和反对称振动模式能量密度，E4为单位体积N2分子振动模式能量密度、E5为CO分子振动模式能量密度、E为环境能量密度，其分别对应T1，T2，T3，T4，T5和 T 这 6 个温度。描述 CO2分子对称振动模式能量密度随时间变化的方程见下式:

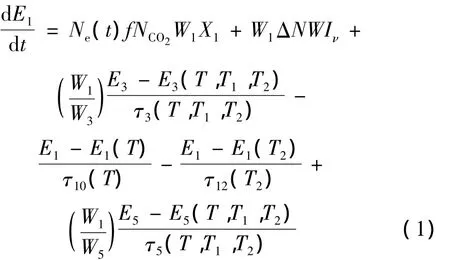
式中，Ne(t)为单位体积的电子密度，f为CO2分子未分解比例，NCO2为单位体积中的CO2分子数量，ΔN为反转粒子数密度，W为中心谱线受激辐射几率，X1为单位体积CO2分子对称振动模式的激励速率，Iν为中心谱线频率 ν对应的激光光强;Wi=hνi(i=1，2，3，4，5)，νi为频率，h 为普朗克常量;E3(T，T1，T2)为单位体积CO2分子反对称振动模式能量密度通过弛豫过程τ3(T，T1，T2)而减少的量;E1(T)为单位体积 CO2分子对称振动模式能量密度通过弛豫过程τ10(T)而减少的量;E1(T2)为单位体积CO2分子对称振动模式能量密度通过弛豫过程τ12(T2)而减少的量;E5(T，T1，T2)为单位体积CO分子振动模式的能量密度通过弛豫过程 τ5(T，T1，T2)而减少的量。

描述CO2分子弯曲振动模式能量密度随时间变化的方程见下式:

式中，X2为单位体积CO2分子弯曲振动模式的激励速率，E2(T)为单位体积CO2分子弯曲振动模式能量密度通过弛豫过程τ20(T)而减少的量。

描述CO2分子反对称振动模式能量密度随时间变化的方程见下式:

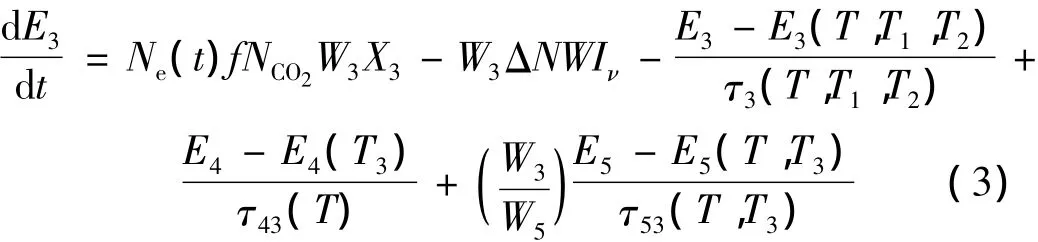
式中，X3为单位体积CO2分子反对称振动模式的激励速率，E4(T3)为单位体积N2分子振动模式能量密度通过弛豫过程τ43(T)而减少的量，E5(T，T3)为单位体积CO分子振动模式能量密度通过弛豫过程τ53(T，T3)而减少的量。

描述N2分子振动模式能量密度随时间变化的方程见下式:

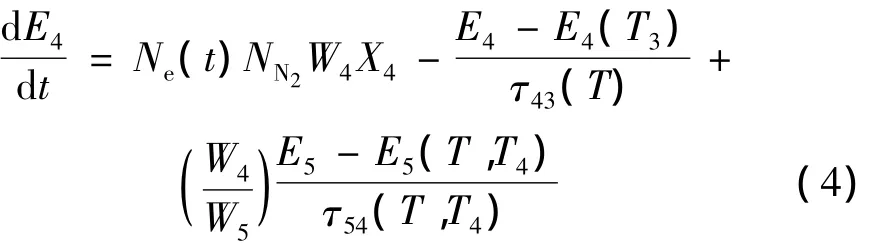
式中，NN2为单位体积中的N2分子数量，X4为单位体积N2分子振动模式的激励速率，E5(T，T4)为单位体积CO分子振动模式能量密度通过弛豫过程τ54(T，T4)而减少的量。

描述CO分子振动模式的能量密度随时间变化的方程见下式:

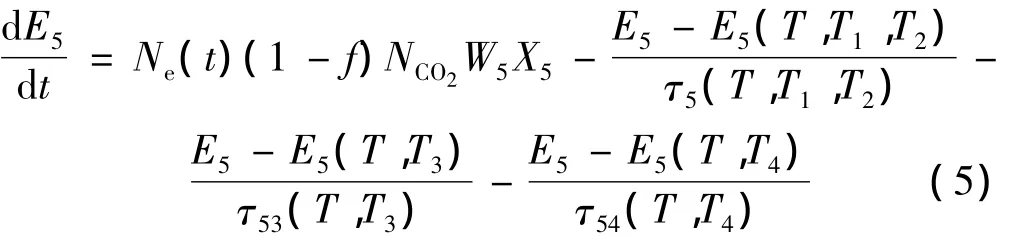
式中，X5为单位体积CO分子振动模式的激励速率。

描述混合气体环境的能量密度随时间变化的方程见下式:

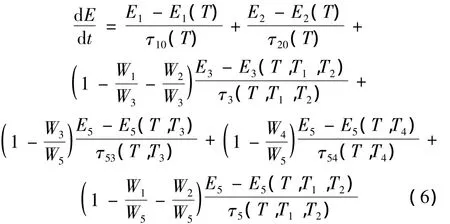
上述6个方程组即是脉冲TEA CO2激光器的六温度模型方程组。除了六温度模型方程组以外，还需要以下描述激光器光强和输出功率的方程才能求解激光器的工作状态。

1．3 激光器光强和输出功率方程

激光光强Iν随时间变化的方程如下式:

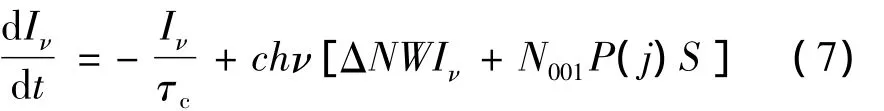
式中，S=4λ2×10-3/(πAτsp)，λ 为发射激光波长，A为激光输出有效截面，c为光速，ν为激光频率，τsp为自发辐射寿命，τc为光腔光子寿命:

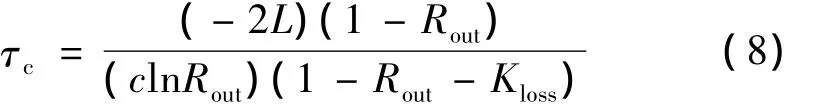
式中，L为激光器腔长，Rout为输出镜反射率，Kloss为损耗系数分别。

激光上下能级的反转粒子数密度ΔN由下式表示:

式中，动常数，j=19，kB为玻尔兹曼常数。

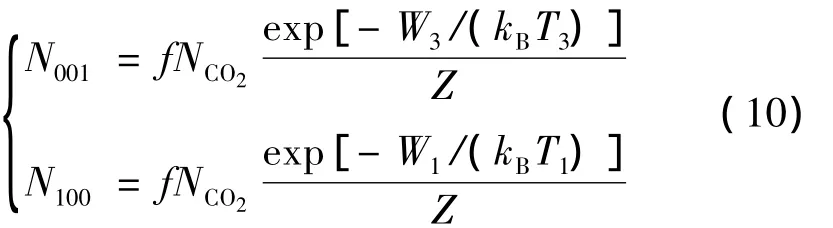
式中，

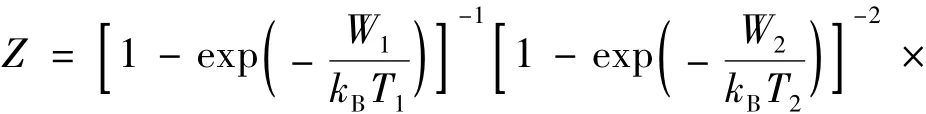
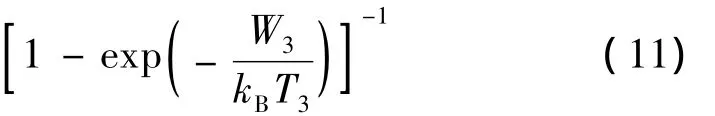
激光输出功率Pout随时间变化的方程见下式:

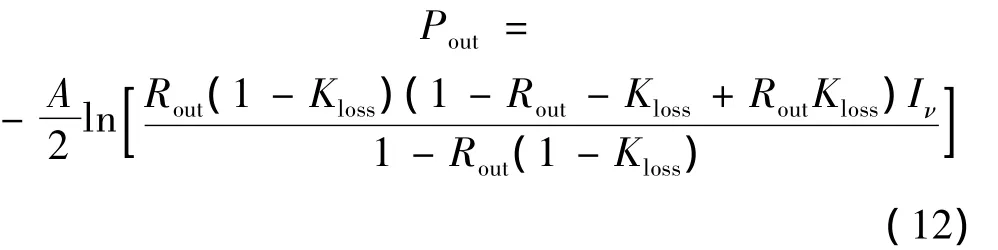
2 数值求解

脉冲TEA CO2激光器的动力学模型由方程(1)式～(6)式描述。运用基于龙格-库塔法的程序来求解上述6个微分方程。文中所需物理参量如表1所示［8-10］。

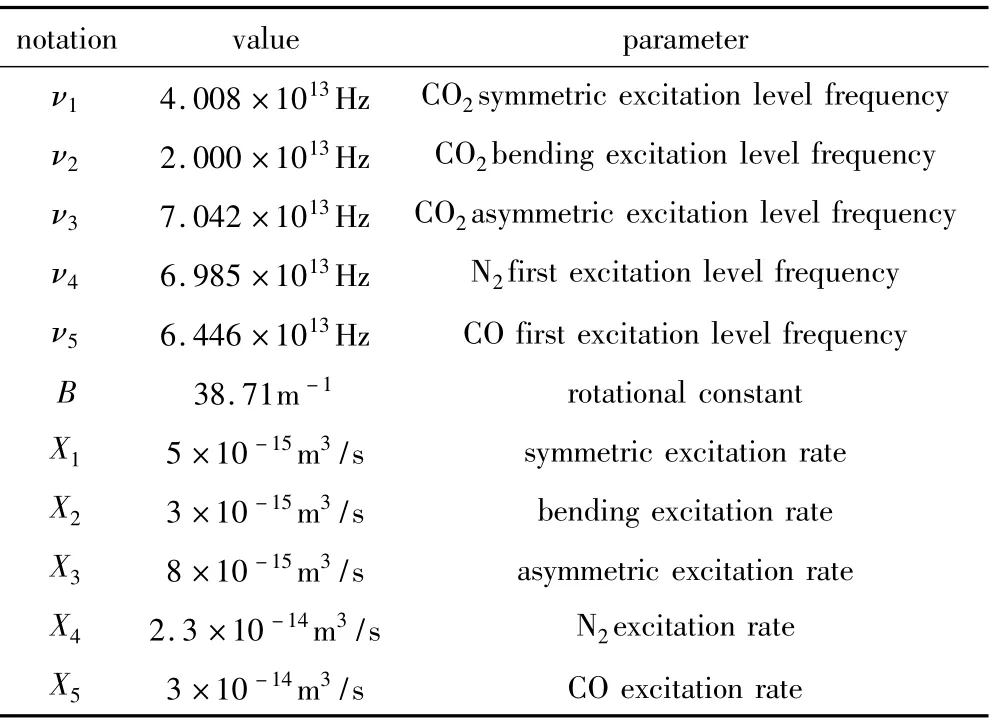
Table 1 Physical parameters

中心谱线受激辐射几率:W=Fλ2/(4π2hνΔντsp)，F为填充因子，F=l/L，l为增益介质长度，Δν为碰撞线宽。NCO2，NN2，NHe分别为单位体积中的CO2分子、N2分子、He分子数量。激光输出有效截面积为1.5cm2，损耗系数为0.001，抽运电子数密度Ne(t)=5 ×1012(1-e-t)e-2t/cm3，T=300K，Iν=10-9J/(cm2·s)。

混合气体的环境能量密度由如下式子表示:

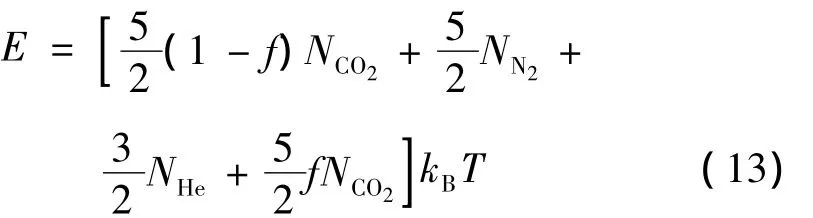
CO2分子对称振动模式能量密度、反对称振动模式能量密度、弯曲振动模式能量密度分别由以下式子表示:

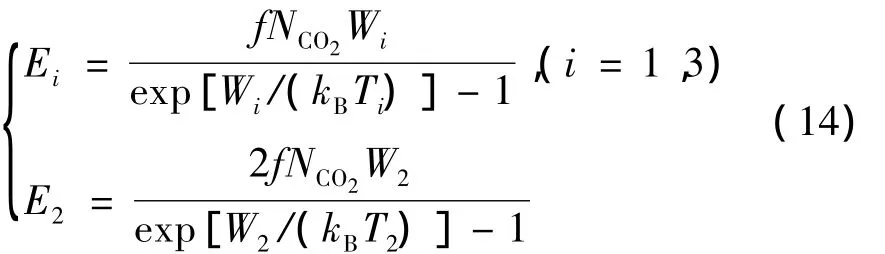
N2分子振动模式能量密度为:

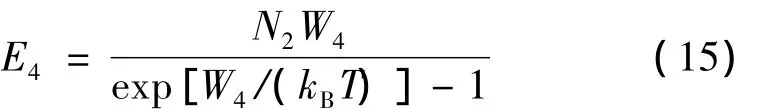
CO分子振动模式的能量密度为:

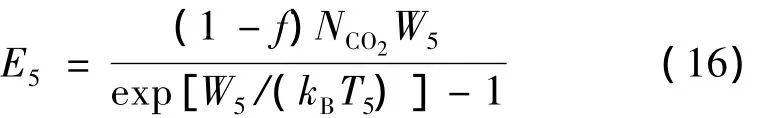
3 模拟结果与分析

在考虑了混合气体分子的碰撞激发、能级转移、受激辐射和自发辐射以及CO2分子分解的情况下，使用基于龙格-库塔法的程序求解方程(1)式～(6)式，然后通过(7)式和(12)式来求得脉冲TEA CO2激光器输出参量特性［11］。

3．1 激光器输出功率与工作气体配比的关系

图2所示是当填充因子为0.9，CO2未分解因子为0.95，腔长为2.5m，输出镜反射率为0.7，Ne(t)最大为5×1012/cm3，CO2，N2，He 的体积比分别为 4∶30∶65，5∶30∶65，6∶30∶65时的脉冲激光输出功率。由图2可知，当CO2比例由4增加到6时，脉冲激光输出功率增加，输出延迟时间变短。CO2比例增加时，受激辐射的CO2分子增加，反转粒子数增加，输出功率变大，有比较大的拖尾现象。可以得出，与N2分子比例相比，CO2分子比例含量的变化对脉冲输出功率的影响较大，这也说明了当CO2存在分解时，将会比较严重地影响到激光输出功率。所以在气体循环封闭性的CO2激光器中通常都会添加CO2催化剂，以防止CO2分子的分解对输出功率的影响。

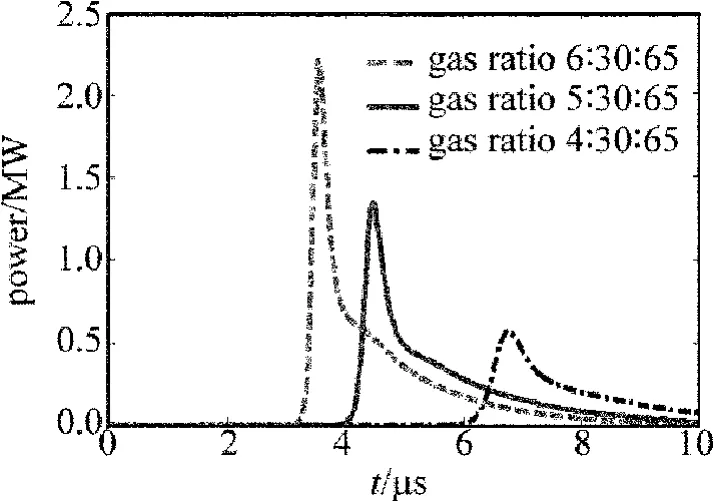
Fig.2 Output power vs.output delay time with different CO2ratio

图3 所示是当填充因子为0.9，CO2未分解因子为0.95，腔长为2.5m，输出镜反射率为0.7，Ne(t)最大为5×1012/cm3，CO2，N2，He 的体积比分别为 5∶15∶65，5∶25∶65，5∶35∶65时的脉冲激光输出功率。由图3可知，当N2比例由15增加到35时，脉冲激光输出功率先增加，然后减少。在 CO2，N2，He 的体积比为 5∶25∶65 附近达到最大值。当N2比例增加时，激光输出延迟时间越长，脉冲拖尾中所含的能量越大。也可以得出当CO2与N2比例增加时，脉冲输出拖尾现象越严重。这是由于当N2一定时，CO2分子比例增加，导致受激辐射激光下能级的CO2分子增加，且激光下能级粒子的停留时间较长，而引起的拖尾现象。这个模拟结果和参考文献［9］中的也是基本吻合的。

Fig.3 Output power vs.output delay time with different N2ratio

3．2 激光器输出功率与抽运电子密度的关系

图4 所示是填充因子为0.9，CO2未分解因子为0.95，腔长为2.5m，输出镜反射率为 0.7，CO2，N2，He的体积比为 5∶30∶65，Ne(t)最大值分别为 4 ×1012/cm3，5×1012/cm3，6 ×1012/cm3时的脉冲激光输出功率。由图4可知，当抽运电子数密度由4×1012/cm3增加到6×1012/cm3时，脉冲激光输出功率增加，激光输出延迟时间越短。抽运电子数密度增加时，CO2分子获得的能量越多，从基态跃迁到高能级的粒子数越多，形成的反转粒子数浓度越大，输出功率变大。同时由于受激辐射跃迁产生激光下能级的CO2分子增加，且激光下能级粒子的停留时间较长，脉冲拖尾中所含的能量越大。这个模拟结果和参考文献［7］中的也是基本吻合的。

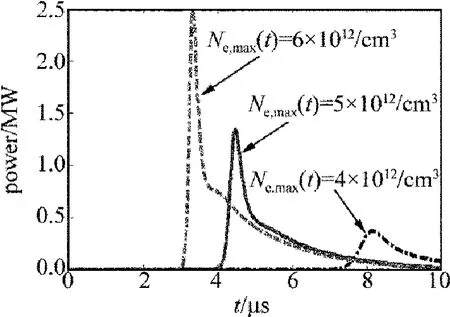
Fig.4 Output power vs.output delay time with different pumping electron numbers

3．3 激光器输出功率与激光器腔长的关系

图5 所示是填充因子为0.9，CO2未分解因子为0.95，输出镜反射率为0.7，Ne(t)最大值为5×1012/cm3，CO2，N2，He 的体积比为 5∶30∶65，腔长分别为 2m，3m和4m时的脉冲激光输出功率。由图5可知，当激光器腔长由2m增加到4m时，脉冲激光输出功率增加，激光输出延迟时间越短。激光腔长增加时，增益介质长度变长，参与形成激光的粒子数更多，输出功率变大。在一定的激光腔长范围内，激光器内增益大于损耗，增加激光器腔长是可以提高激光输出功率的。这个模拟结果和参考文献［10］中的也是基本吻合的。

Fig.5 Output power vs.output delay time with different cavity lengths

4 结论

六温度模型能够用来模拟脉冲TEA CO2激光器输出特性。激光器的气体配比、抽运电子数密度、腔长都对脉冲输出功率有影响，在设计和优化激光器时可以作为参考。

(1)在N2和He比例固定为30∶65，CO2的比例由4上升到6时，脉冲激光输出功率有明显的增加，激光输出延迟时间越短，但同时有更长的拖尾现象。CO2分子比例的变化对脉冲输出的功率影响较大。

(2)在 CO2和 He比例固定为 5∶65，N2的比例由15上升到35时，脉冲激光输出功率按先增加后减小的趋势变化，在N2比例约为25时，达到最大。脉冲输出功率越大时，激光输出延迟时间越短，但有更长的拖尾现象。

(3)在 CO2，N2，He 的比例为 5∶30∶65 时，当 Ne(t)最大值由4×1012/cm3增加到6×1012/cm3、腔长由2m增加到4m时，脉冲激光输出功率逐渐增加。

［1］ RUDOLPH R，HARENDT A，BISIN P，et al.Numerical modelling of fast flow CO2lasers.Ⅰ:the model［J］.Journal of Physics，1993，D26(4):552-559.

［2］ SMITH K，THOMSON R M.Computer modeling of gas laser［M］.New York，USA:Plenum Press，1978:1-87.

［3］ LU Y Z，WANG X B，DONG J，et al.Pulse characteristics of a dual wavelength tunable TEA CO2laser［J］.Laser Technology，2010，34(1):88-90(in Chinese).

［4］ DING C L，WAN C Y.Multifrequency dynamical model of pulsed CO2lasers［J］.Acta Physica Sinica，2006，55(3):1165-1170(in Chinese).

［5］ TIAN Z S，WANG Q，WANG Y S.Kinetic modeling of electroopitcally Q-switched CO2laser［J］.Optical and Quantum Electronics，2002，34(2):331-341.

［6］ JELVANI S，SAEEDI H.Numerical investigation of a fast axial flow CW CO2laser［J］.Optics ＆ Laser Technology，2008，40(3):459-465.

［7］ KOUHKI A M，JELVANI S，SILAKHORI K，et al.Kinetic modeling of a pulsed CO2laser［J］.Lasers Engineering，2011，21(5):265-280.

［8］ TOEBART D，MUYS P，DESOPPERE E.Theoretical study of the properties of a modulated fast flow CO2laser［J］.Infrared Physics ＆Technology，1997，38(6):337-355.

［9］ SOUKIEH M，GHANI B A，HAMMADI M.Mathematical modeling of CO2TEA laser［J］.Optics ＆ Laser Technology，1998，30(8):451-457.

［10］ DING C L.Theoretical study of the dynamics of multi frequency pulse CO2laser［D］.Beijing:Graduate University of Chinese A-cademy of Sciences，2006:17-37(in Chinese).

［11］ LI H.Numerical analysis［M］.Wuhan:Huazhong University of Science and Technology Press，2010:125-142(in Chinese).