燃气轮机鼓筒的热应力分析及结构优化

燃气轮机鼓筒的热应力分析及结构优化

施培丽,李海伟

上海电气集团股份有限公司 中央研究院，上海 200070

摘要：通过有限元软件建立转子热固耦合模型，着重对燃气轮机鼓筒进行热应力分析。研究表明，启动过程和停机过程中的热应力最大值区域均集中在燃机鼓筒的内外倒角处，且应力值均已超过材料的屈服极限。对鼓筒进行结构优化的研究后发现，若要同时减小圆角处的热应力值，在材料和加工允许的范围内，最好同时增大鼓筒靠近压机端的内外圆倒角R1和R2的值。

关键词：鼓筒； 热应力； 热固耦合； 结构优化

燃气轮机转子运行在温度很高的环境下，转子的材料因环境温度的变化而热胀冷缩产生热应力。冷态启动过程中转子被蒸汽加热，转子表面温度快速上升，并受压应力作用；停机过程则相反，转子表面受拉应力作用。启、停机过程中，转子表面的热应力发生拉、压变化，导致转子产生疲劳寿命消耗，严重时威胁整个机组的安全运行1]。鼓筒作为燃气轮机传递扭矩的核心部件，其热力学特性对燃气轮机运行的稳定性、安全性、振动特性及使用寿命等有着重要影响。当鼓筒存在应力集中现象、某些部位的应力超过材料的屈服极限时，就可能导致转子产生疲劳损伤，甚至出现裂纹，乃至发生断裂。

在以往的研究中，多认为降低转子热应力的最好办法是降低蒸汽的温升率，然而降低温升率会导致启动时间变长。但在目前国际能源短缺、环境污染压力及电网调峰的需要，都要求机组能够快速启动2]。因此，在缩短启动时间的前提下，通过优化转子的尺寸结构来降低转子热应力具有重要的应用前景。随着计算机技术的发展，基于有限元的高精度数值解法越来越多地应用于旋转机械热应力的计算中3]。本文通过有限元软件来分析某燃气轮机鼓筒在高温条件下启动过程中的热应力，并对应力集中区域进行尺寸结构优化。

1热应力分析及有限元计算

1.1　温度场计算方程

在分析转子热应力的过程中，往往要结合顺序耦合分析的方法，即首先添加热边界条件对转子本身进行温度场分析，然后导入温度场对转子进行热应力分析。计算燃气轮机转子温度t时，可以假定温度分布沿轴向是相同的，因此可以认为转子温度分布仅是径向坐标r、轴向坐标z以及时间τ的函数，可以认为其是一个轴对称、均匀、各向同性且无内热源的二维导热问题，温度场满足下列方程4]：

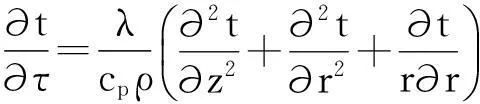
(1)

式中：λ为材料的热导率；ρ为材料的密度；cp为材料的比热。

瞬态导热问题有如下三类边界条件。

(1) 第一类边界条件，规定固体边界上的温度值tw，即:

tw=f1(τ)

(2)

(2) 第二类边界条件，规定了固体边界上的热流密度值，即：

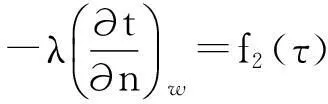
(3)

式中：n为表面的法线方向。

(3) 第三类边界条件，规定了固体边界上物体与周围流体间的表面传热系数h及周围流体的温度tf，即：

(4)

本文采用第一类边界条件，即规定燃气轮机转子固体边界的温度值随时间的变化。

1.2　热应力基本公式

热应力的基本计算式2]为：

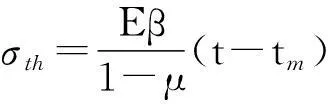
(5)

式中：σth为热应力，MPa；E为材料的弹性模量，MPa；μ为泊松比；β为材料的线膨胀系数，℃-1；tm为物体的体积平均温度，℃；t为计算点的温度，℃。

对于轴对称截面，体积平均温度的计算由式(6)确定，即：

(6)

式中：R1、R2分别为轴对称物体的外半径和内半径。

根据以上公式，影响热应力的因素包括： 材料的性质、温差的大小、加载的方式、温度变化率等，而当材料的性质和加载方式一定时，热应力仅取决于物体内部的温度分布规律，影响温度分布规律的因素则有结构因素、蒸汽参数的变化量和变化率等5、6]。所以，本文通过改变燃气轮机鼓筒的结构尺寸来改变热应力的分布。

2模型及边界条件

2.1　模型

计算模型采用的是二维轴对称截面，该截面是用一个通过轴线的平面切割后形成的平面的一半，如图1所示，该二维模型忽略了拉杆和拉杆孔。网格划分为结构化网格，数量为10012，如图2所示。

图1　二维轴对称截面的截取

图2网格划分

2.2　边界条件

(1) 启动过程的温度条件。图3为燃机鼓筒表面的温度值随时间的变化情况，启动时间(燃机启动至额定转速)为272.61s，1～2为点火时刻，3为点火后进口温度的峰值，4为峰值后的低谷值，5为接近满转速空负荷时的温度值。

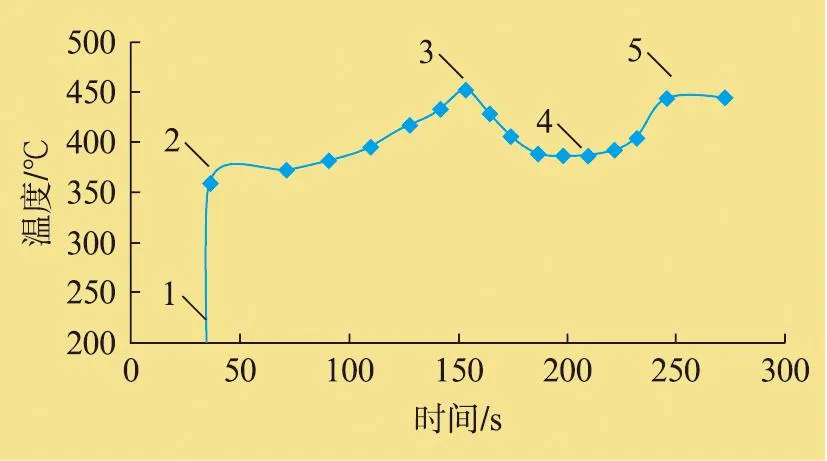
图3　燃机鼓筒表面的温度值随时间的变化

(2) 停机过程的温度条件。因为没有停机惰走过程的计算书，所以按试验测定的曲线取点，其中燃机端的固体表面温度随时间的变化见表1。

表1　燃机端温度

3启动和停机过程中的热应力分析

3.1　启动过程中的热应力分析

从图4、5可知，启动过程中应力最大值区域主要集中在燃机鼓筒及压机鼓筒的倒角处(图5高亮显示)。分别选取燃机鼓筒和压机鼓筒内外倒角的应力时程曲线，如图6所示，从图中可以看到，燃机鼓筒和压机鼓筒的应力从0s开始慢慢增大，到τ=300s时应力达到最大值，这是由于此刻鼓筒倒角的温度梯度较大，随后应力值慢慢降低至稳定状态。应力最大值在时刻τ=300s时，燃机鼓筒内倒角的最大应力值为661MPa，外倒角的最大应力值为507MPa；压机鼓筒内倒角的最大应力值为484MPa，外倒角的最大应力值为520MPa。此时燃机鼓筒应力已经超过材料的极限屈服应力582MPa，对于鼓筒材料的强度以及整个转子运行寿命有较大影响。

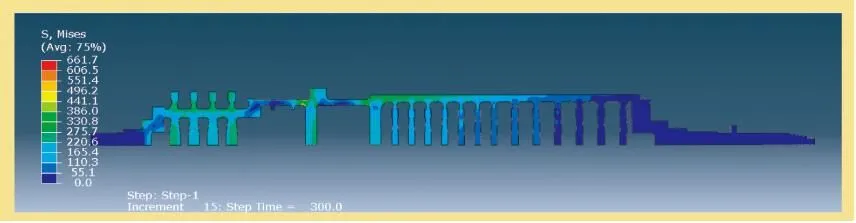
图4　τ=300s时转子的应力分布

图5　应力最大值局部放大区域

图6　启动过程中燃机与压机鼓筒内外倒角的时程应力曲线

3.2　停机过程中的热应力分析

转子温度冷却的过程是外表面的温度最先降低，随后各轮盘中心也逐渐降低，经过2.6h转子完全达到环境温度。图7表明，停机过程中应力最大值区域也主要集中在燃机鼓筒及压机鼓筒的倒角处。分别选取燃机鼓筒和压机鼓筒内外倒角的应力时程曲线，如图8所示，从图上可以看到，应力最大值均在时刻τ=159s，燃机鼓筒内倒角的最大应力值为688MPa，外倒角的最大应力值为567MPa；压机鼓筒内倒角的最大应力值为466MPa，外倒角的最大应力值为580MPa。经过159s后，燃机鼓筒和压机鼓筒的内外倒角的应力值逐渐降低，这可为优化结构、降低极值应力提供依据。

图7　τ=159.8s时转子的应力分布

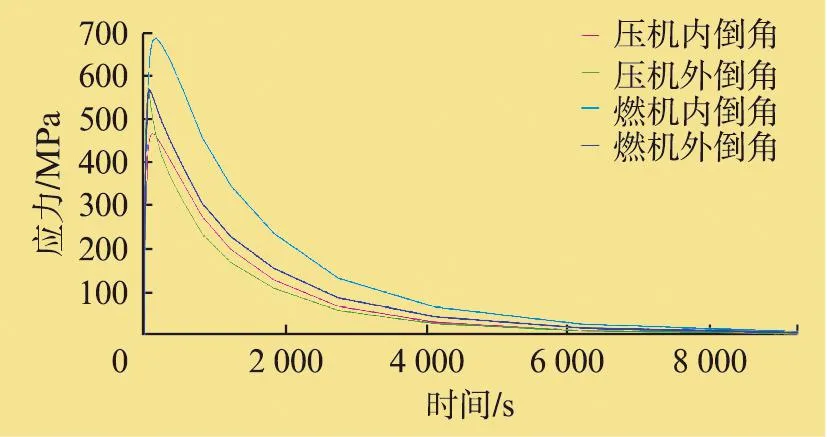
图8　停机过程中燃机与压机鼓筒内外倒角的时程应力曲线

4燃机段鼓筒的结构尺寸优化

通过对燃气轮机转子热应力的分析，得到转子应力最大的位置分布在燃机段鼓筒和压机段鼓筒的内外倒角处，由此对燃机段的鼓筒单独进行热应力分析，对其结构进行优化。图9所示为拉杆转子2维轴对称模型，用红色线框标识的为燃机端鼓筒。

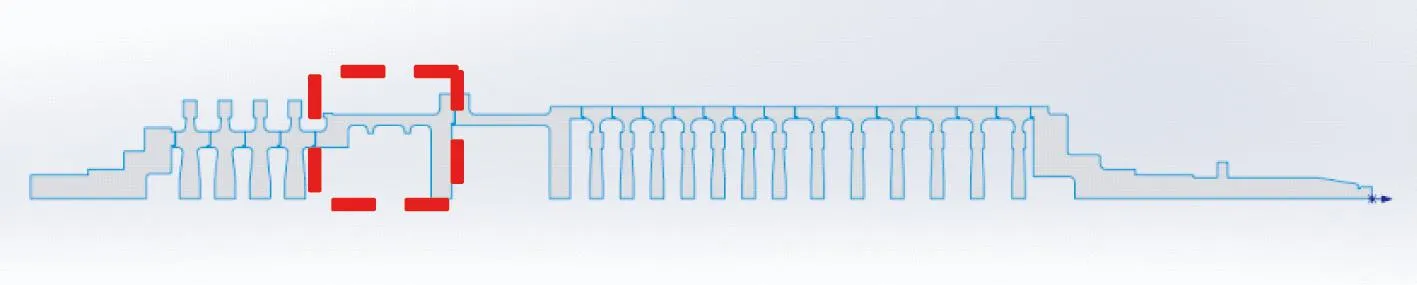
图9　拉杆转子模型

图10为燃机端鼓筒模型，用红色线框标识的是需要优化的半径尺寸R1和R2。R1和R2的值从10mm变化到30mm，其参考值为20mm。

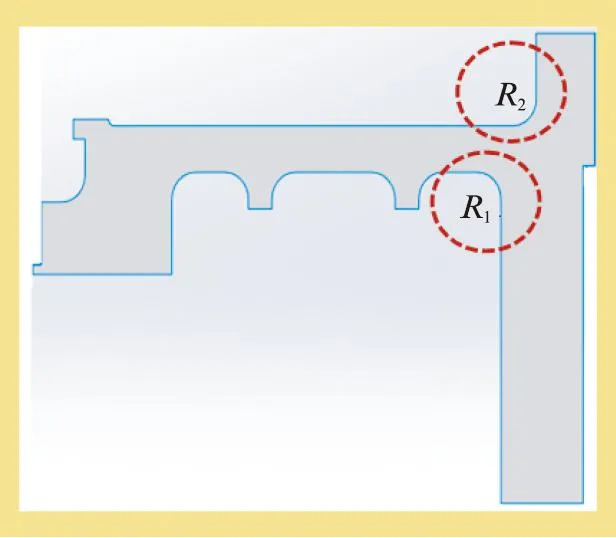
图10　燃机端鼓筒模型

4.1　R1尺寸变化对热应力的影响分析

为了得到燃机鼓筒热应力随倒角参数的变化趋势，采用边界条件为稳态运行下的温度条件。计算出在R2=20mm、R1=10、11、12、13、14、15、16、17、18、19、20、21、22、23、24、25、26、27、28、29、30mm等尺寸下拉杆转子的热应力，在燃机端鼓筒所示的两个圆角处会出现应力集中。由图11和图12的曲线可知，R1处的最大应力随R1的增大而减小，从26MPa近似线性减小到21MPa，其变化幅度约为23.8%。R2处的最大应力随R1的增大而增大，从24.7MPa近似线性增大到25.8MPa，其变化幅度约为4.5%。

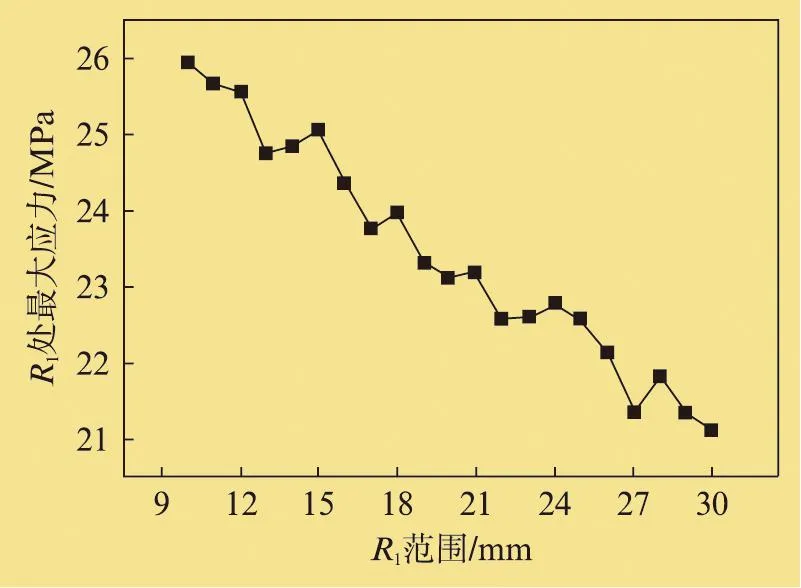
图11　R1处最大应力随R1值的变化

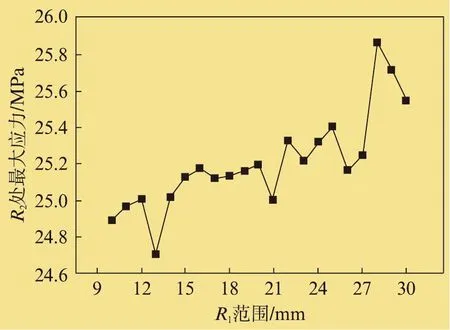
图12　R2处最大应力随R1值的变化

从计算结果分析可得，当R1尺寸增大时，可减小R1处的最大热应力，在R2处的热应力会有所增大，但增幅较小。

4.2　R2尺寸变化对热应力的影响分析

计算出在R1=20mm、R2=10、11、12、13、14、15、16、17、18、19、20、21、22、23、24、25、26、27、28、29、30mm等尺寸下拉杆转子的热应力，在燃机端鼓筒所示的两个圆角处会出现应力集中。从图13和图14的曲线可知，R1处的最大应力随R2的增大而增大，从21.8MPa近似线性增大到25MPa，其变化幅度约为14.9%。R2处的最大应力随R2的增大而线性减小，从31MPa减小到22.5MPa，其变化幅度约为27.4%。

图13　R1处最大应力随R2值的变化

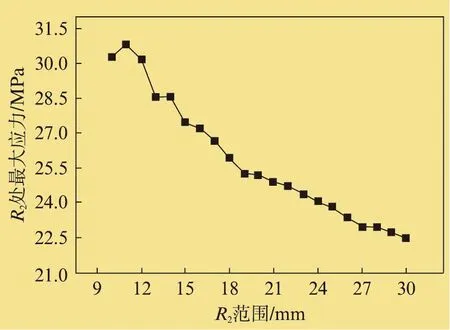
图14　R2处最大应力随R2值的变化

从计算结果分析可得，当R2尺寸增大时，可减小R2处的最大热应力，在R1处的热应力会有所增大，但增幅较小。因此，综合上述计算可知，若要减小圆角处的热应力集中，在材料和加工允许的范围内，可同时增大R1和R2的值。

5结束语

本文通过有限元软件对燃气轮机鼓筒进行热应力分析，从中可以得到以下结论。

(1) 启动过程和停机过程中的热应力最大值区域均集中在燃机鼓筒的内外倒角处。启动过程中，鼓筒应力在300s时刻附近，最大值为661MPa；停机过程中，鼓筒应力在159s时刻附近，最大值为688MPa。这两个时刻的应力值均超过了鼓筒材料的屈服极限，对转子的运行寿命有较大影响。

(2) 从计算结果分析可得，当燃机鼓筒内半径R1尺寸增大时，R1处的最大热应力减小，但在燃机鼓筒外半径R2处的热应力会有所增大，但增幅较小。当R2尺寸增大时，R2处的最大热应力减小，在R1处的热应力会有所增大，但增幅较小。

(3) 从两个半径的变化对热应力大小的影响趋势来看，若要减小圆角处的热应力集中，在材料和加工允许的范围内，最好同时增大R1和R2的值。

参考文献

1] 徐自力,王凯，方宇，等.汽轮机启动过程温升分配对转子热应力的影响J].机械工程学报,2013，49(12)： 69-70.

2] 郑李鹏.基于APDL的联合循环汽轮机转子热应力计算及启动优化的研究D].杭州： 浙江大学,2011： 5-9.

3] 高锐，袁奇，高进.燃气轮机拉杆转子有限元模型研究及临界转速计算J].热能动力工程,2009,24(3)： 305-308.

4] 韩炜,何青,沈克伟，等.1000MW超超临界汽轮机转子启动过程的热应力分析J].华电技术,2013,35(2)： 27-32.

5] 张保横.大容量火电机组寿命管理与调峰运行M].北京： 水利电力出版社,1988.

6] 李维特.热应力理论分析及应用M].北京： 中国电力出版社,2004.

Thermal Stress Analysis and Structural

Optimization of Gas Turbine Drum

ShiPeili，LiHaiwei

Shanghai Electric Group Co., Ltd., Central Academe, Shanghai 200070, China

Abstract:Rotor thermosetting coupling model was established via finite element software and the model was focusing on thermal stress analysis of the gas turbine drum. The study had shown that the maximum thermal stresses are concentrated at the inner and outer chamfer areas of the gas turbine drum during startup and shutdown and the magnitude of stress exceeds the yield limit of the material. It was found after structural optimization of the drum, if the thermal stresses at the filleted corners need to be reduced at the same time, the best way was to increase simultaneously the inner and outer chamfer values R1 and R2 at the drum side nearby the press end provided it was within the allowed ranges of the materials and the processes.

Key Words:Drum; Thermal Stress; Thermal-structure Coupling Analysis; Structure Optimization

中图分类号:TK 47

文献标识码:A

文章编号：1674-540X(2015)01-031-05

作者简介：施培丽(1987-)，女，硕士，主要从事叶轮机械力学特性的研究工作，
E-mail： please125@126.com

收稿日期：2014-10-22