大型复杂回转机械装置齿轮啮合的精确建模及仿真

大型复杂回转机械装置齿轮啮合的精确建模及仿真

杜跃斐，龙亚文

上海电气集团股份有限公司 中央研究院，上海 200070

摘要：采用SolidWorks三维建模软件，根据齿轮渐开线方程，建立了齿轮精确三维几何模型。使用Hypermesh专业网格划分工具，对齿轮几何模型进行有限元网格划分，为获得精确的计算结果，在啮合区域进行了网格加密处理。最后采用ANSYS分析软件建立了齿轮啮合模型，计算了齿轮啮合时的变形和接触应力，对于齿轮接触强度的设计具有重要参考价值。

关键词：齿轮建模； 网格加密； 接触应力； 齿轮间隙

齿轮传动因其具有恒功率传动特性，与其他传动相比，有着不可替代的优势，其高质量高性能研究已经成为我国能源、交通、化工、冶金领域重大的共性关键技术。目前国内汽车工业、机械装备、火车机车、电子、航空、航天、船舶及风力发电等传动系统均已广泛采用齿轮传动1]，齿轮设计与传动分析在机械领域中占据着越来越重要的地位。近年来，随着CAD/CAE技术不断应用到齿轮设计与分析领域，很多学者对此开展了大量的工作，并取得了许多成果2,3]。随着时代的进步，设计者对齿轮的静态、动态性能的要求也随之提高，齿轮传动正朝着较高的齿轮转速、较大的齿轮承载能力、较轻的整机质量及更精密的传动精度方向发展。

1目前存在的问题

在齿轮啮合过程中，齿轮间接触强度影响齿轮承载能力，进而会影响到齿轮的寿命。很多齿轮失效如齿轮点蚀等，均是由于齿轮接触强度不足引起的。齿轮齿面接触强度是齿轮设计准则之一，齿轮设计的另一个问题是齿轮齿形误差，即齿轮齿廓形状偏离理想齿廓。齿形误差会改变原有的齿轮齿面接触面积和齿轮啮合状态，进而影响到齿轮啮合过程中的应力和变形，而且它的随机性给齿轮强度设计和齿轮啮合刚度计算带来了较大的困难。

本文基于有限元法，精确建立理想齿廓齿轮有限元模型，用于计算齿轮的接触应力和啮合刚度。同时考虑了由于装配引起的齿轮啮合误差对计算结果的影响。

2几何建模

若齿轮齿廓为渐开线，在SolidWorks中精确建立几何模型时，需要首先将渐开线以数学形式描述出来，其方程为：

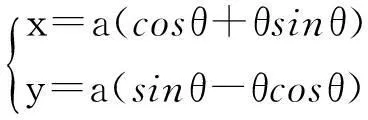
(1)

式中：a为基圆半径；θ为极轴角度。

由渐开线的直角坐标方程得到的参数方程对渐开线建模有两种途径4]： ① 描点法，取不同参数得到有限个渐开线上的离散点，之后将这些点利用样条曲线等工具进行拟合得到相应齿廓；② 法则曲线法，使用法则曲线工具分别绘制x、y关于自变量的空间曲线，之后将两条曲线利用混合、投影等工具得到y关于x的曲线即渐开线，最终得到相应齿廓。

Gear Trax是目前最流行的齿轮建模插件之一，主要用于精确齿轮的自动设计和齿轮副的设计，通过指定齿轮类型、模数、齿数、压力角以及其他相关参数，可以自动生成具有精确齿形的齿轮，如图1所示。

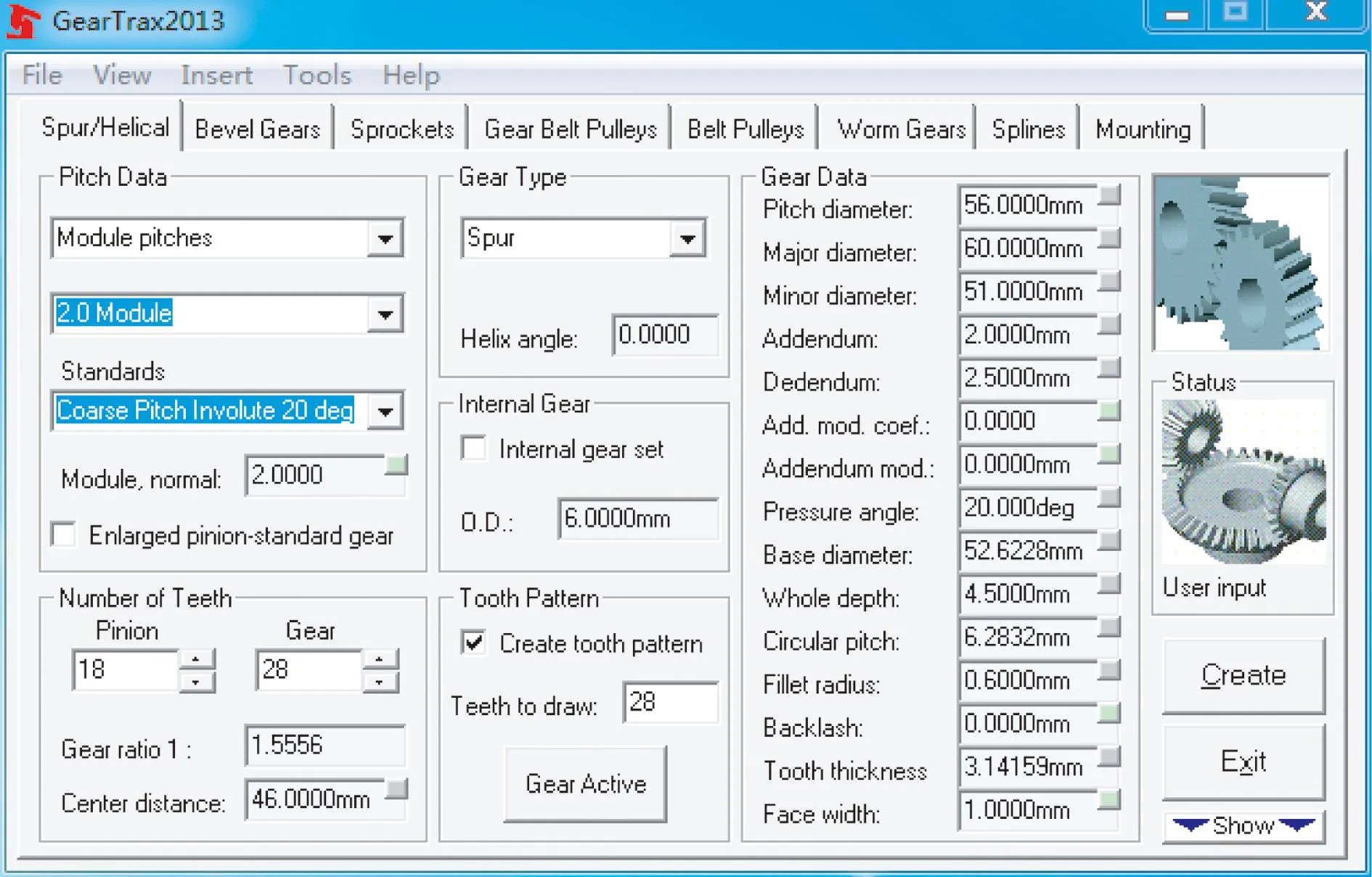
图1　Gear Trax2013设置界面

启动Gear Trax2013，输入相应的模数和齿数，点击生成按钮，即可在SolidWorks中生成图2(a)所示的齿廓，然后可在SolidWorks中进行特征阵列和拉伸命令，即可生成完整的齿轮精确模型，如图2(b)、(c)、(d)所示。

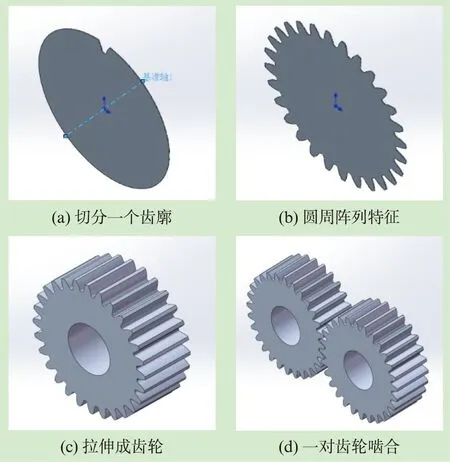
图2　齿轮建模步骤

3齿轮啮合静力学分析

因齿轮啮合过程而产生的周期性的变形是引起齿轮刚度激励的原因，轮齿变形的大小直接影响齿轮的啮合刚度。齿轮啮合刚度是齿轮动力学研究的基础，同时，研究齿轮轮齿变形和啮合刚度对齿轮传动精度研究和齿轮动力学性能研究很有意义。

有限元方法计算齿轮啮合刚度时，首先要建立齿轮三维实体模型，然后将齿轮实体模型划分有限元网格，得到齿轮有限元模型，最后根据实际工况加载，计算齿轮变形量。20世纪70年代以来，随着计算机技术和有限元方法在各领域中的广泛应用，专家和学者们开始利用有限元接触算法来求解齿轮变形及齿轮啮合刚度问题。

3.1　标准接触算法

有限元接触算法以弹性理论为基础，适用于求解一对或多对轮齿啮合时的齿轮变形问题，这种变形包括齿轮轮齿的弯曲变形、剪切变形及齿轮接触变形等。

在齿轮啮合过程中，齿轮内部满足弹性力学的平衡方程、几何方程和本构方程，在齿轮啮合面之间需满足接触边界条件。

(1) 平衡方程：

(2)

(3)

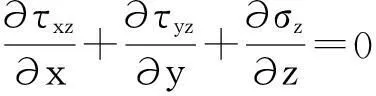
(4)

式中：σx、σy、σz为正应力；τxy、τxz、τzx为剪应力；x、y、z为三个方向坐标。

(2) 几何方程：

(5)

(6)

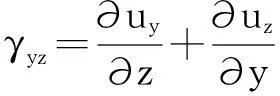
(7)

(8)

式中：εx、εy、εz为正应变；γxy、γyz、γxz为剪应变；ux、uy、uz为位移。

(3) 本构方程：

(9)

(10)

(11)

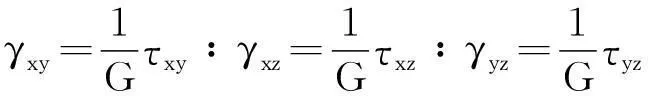
(12)

式中：E为弹性模量；v为泊松比；G为剪切模量。

(4) 接触边界条件：

不可贯入条件：

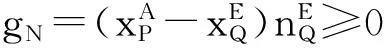
(13)

法向接触力为压力：

(14)

切向接触力为0：

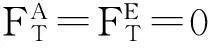
(15)

3.2　网格划分方案

齿轮实体模型网格划分的单元数量规模关系到齿轮有限元模型计算时间的长短，网格质量及接触区网格细密程度关系到有限元接触分析计算的准确性。齿轮模型的接触区为高副接触，这对齿轮有限元模型接触部分网格密度提出了更高的要求，需要细密网格以得到满意的计算结果，其他区域网格用于传递载荷和约束，不需要细密网格。

本文将齿轮接触部分和其余部分分别应用不同的方式划分网格，其余部分应用自适应网格和映射网格两种划分方式，可得到数量较少且质量较好网格，如图3所示。

图3　齿轮网格

3.3　计算相关设置

本文采用两齿轮接触齿面间建立接触对的方式建立齿轮接触关系，齿轮啮合的具体位置根据变形情况自动搜索确定，从而可以精确得到齿轮啮合时的变形，保证了齿轮变形计算的准确性。对于接触对，ANSYS内部定义了接触单元Conta 173和目标单元Targe170两种接触单元。分别选定主、从动轮接触部分齿面节点为接触单元组集和目标单元组集，并在相互啮合的两轮齿模型节点组建立接触关系。

加载过程分为主、从动轮约束和载荷的施加以及接触对的建立。对于主动轮，在主动轮中心建立节点，以中心点为主节点将内孔节点耦合至中心节点，在中心节点施加轴向和径向约束，保留轴向旋转自由度并施加大小为1.0×105N·m的扭矩。对于从动轮，将内孔节点三个方向自由度全部约束。

3.4　计算结果分析

从表1和图4可得主动轮的最大位移为56.7μm，大于从动轮的最大位移32.4μm。主动轮最大位移出现在非接触区域的齿根上，而从动轮的最大位移出现在接触区域的齿根上，这与外载荷的施加和位移约束有关。

表1　静力学计算结果

主动轮计算所得最大等效应力为367MPa，从动轮最大等效应力为453MPa，其应力分布如图4(b)、(d)所示，为沿齿根厚度方向狭窄的长方形区域。

齿轮的刚度采用日本机械学会的定义，即把每单位齿宽的载荷和每个齿轮轮齿面法向变形量的和的比值定义为一对轮齿的刚度。若以Fn表示轮齿所受的法向力，以B表示齿轮齿宽，以δ表示齿轮所有轮齿齿面法向变形的和，则啮合刚度kn有如下表达式：

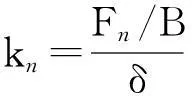
(16)

式中： 轮齿总变形δ是包括齿轮的弯曲变形、剪切变形和接触变形等所有变形的总和。

4装配误差对齿轮计算结果的影响

在齿轮安装或者装配过程中，齿轮相互较难保证理想的啮合状态，可能会存在一些偏差，会对齿轮啮合时接触应力和啮合刚度造成一定的影响，影响到齿轮的接触强度及齿轮传动的平稳性。若误差较大，则齿轮更容易引起破坏，齿轮传动系统也更容易产生振动、噪声，严重时还可引起齿轮箱体共振，从而破坏齿轮原有的传动性能。

本文以完全啮合为基准(即两个齿轮分度圆半径相切时为理想啮合状态)，计算了在两个齿轮圆心相互远离(啮合间隙)到2mm距离过程中，齿轮的位移和应力的变化趋势。

图4　齿轮计算结果

从图5(a)可知，随着啮合间隙的增大，主动轮最大位移大致为减小的趋势，其变化量约为10%。图5(b)所示最大等效应力先增大后减小，随后再增大，最大应力点与接触位置的变化有关，变化幅度大约为50%。

从图5(c)可知，随着啮合间隙的增大，从动轮最大位移大致为增加的趋势，其变化量约为7%，变化趋势与主动轮相反。图5(d)所示为从动轮最大等效应力的变化，最大应力点与接触位置的变化有关，变化幅度大约为60%。

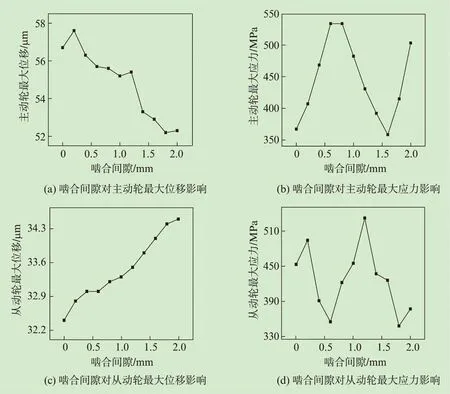
图5　啮合间隙大小对计算结果的影响

由以上分析可知，为保证精确计算齿轮的接触应力与接触刚度，必须将齿轮有限元接触模型在几何上的误差控制在较小的范围内。

5结论

(1) 本文根据齿廓渐开线方程和三维建模软件SolidWorks建立了精确的三维齿轮几何模型。

(2) 采用有限元接触算法计算了一对齿轮啮合过程中啮合面上的接触应力和变形量，为齿轮设计提供了数据支撑。这种计算方法还可推广到多对齿轮啮合的工况，具有较强的通用性。

(3) 计算了由装配误差造成啮合存在间隙时，接触应力和变形随啮合间隙的影响规律和变化幅度。若采用有限元方法进行齿轮啮合计算时，需要保证齿轮啮合几何误差控制在较小的范围内才能获得较精确的解。

参考文献

1] 乔福瑞.基于ANSYS的齿轮接触应力与啮合刚度研究D].大连： 大连理工大学，2013.

2] 孙建国.渐开线圆柱齿轮修形及动力接触特性研究D].重庆： 重庆大学，2008.

3] 王钦.基于接触分析的齿轮建模和齿轮修形研究D].大连： 大连理工大学，2008.

4] 范小钢，徐辅仁，隋鹏，等.基于齿数的渐开线直齿轮参数化建模J].航空精密制造技术，2005,41(1)： 60-62.

Accurate Modeling and Simulation of Gear Meshing in

Large & Complex Rotary Machine Unit

DuYuefei,LongYawen

Shanghai Electric Group Co., Ltd. Central Academe, Shanghai 200070, China

Abstract:SolidWorks 3-D modeling software was used to establish 3-D geometrical model precisely in accordance with the gear involute equation. Hypermesh professional meshing tool was used to achieve finite element meshing for the gear geometrical model. In order to obtain accurate results, the meshing area had been processed through grid refinement. ANSYS software was adopted to establish a gear meshing model and calculate the deformation and contact stress during gear meshing that will present an important reference when designing the contact strength of the gears.

Key Words:Gear Modeling; Mesh Refinement; Contact Stress; Gear Gap

中图分类号:TH 132.4

文献标识码:A

文章编号：1674-540X(2015)01-009-05

作者简介：杜跃斐(1988-)，男，助理工程师，主要从事CAE仿真分析工作，
E-mail： duyuefeilo@126.com

收稿日期：2014-10-23