基于SPSS 软件的因子分析

魏 威，王诗雨

(1.郑州铁路职业技术学院，河南 郑州 450052;2.大众汽车变速器有限公司，天津 300462)

0 概述

SPSS(Statistical Product and Service Solutions)是由SPSS 公司于1968 年开发的一款数据分析软件，它拥有易于操作的图形界面，包含有标准的数据分析方法和多个进行统计数据和指标制图系统，如因子分析(factor analysis)、回归分析(regression analysis)等。

因子分析是一种用于检查基本结构如何影响一些需要测量变量结果的方法集合，它可将同类因子整合在一起，减少整体数据量。目前，使用SPSS 软件进行因子分析多用于经济和社会层面，例如:消费者习惯研究、市场调查研究、产品分类等，通过因子分析可将多个复杂的数据整合在一起，缩减成不同因子，得出重要指标，为管理者在短时间内找到问题所在，做出决策提供依据。

进行因子分析一般需要50～1000 个样本数据，但经验表明，有10 个以上样本数据也可进行因子分析。本文以德国16 个城市(Stadt)的垃圾(Müll)、街道(Straβe)、水(Wasser)、天 然 气(Gas)、电 力(Strom)和地税(Steuer)数据为案例，利用SPSS 软件数据视图(dataview)和变量视图(variableview)，对案例进行因子分析。表1 是用数据视图显示的案例数据，表2 是用变量视图显示的案例数据，表2 标签(label)一栏，是变量单位。

表1 数据视图显示的案例数据

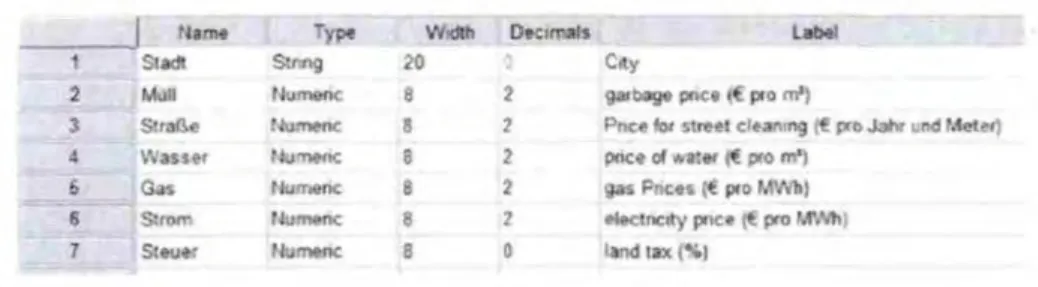
表2 变量视图显示的案例数据

1 SPSS 输出结果分析(因子分析)

使用SPSS 数据分析软件进行因子分析，重点是对最后生成的若干表格进行分析，从而将属于同一分子下的因素整合在一起。做因子分析的前提是要做KMO 和巴特利特球形检验来判断所得结果是否适合做因子分析。

(1)KMO 和巴特利球形检验

KMO 是检验统计量，它可用来比较变量间简单相关系数和偏相关系数指标。检验统计量取值一般应在0～1 之间，它是一个检查因子分析合适性的指标。统计量越接近1，就越适合做因子分析，0.6 是建议的最低值。在此案例中KMO 值为0.601(见表3)，虽然不是很适合做因子分析，但属于中等偏下。

表3 KMO 和巴特利特球形测试

巴特利特球形检验是以相关矩阵为基础，来判断相关数矩阵对角线的所有元素是否为1，所有非对角线上的元素是否均为零。当Sig.(Significance)数值小于0.05 时，则不适合做因子分析。而表3 中Sig.的数值为0.505，可进行因子分析，但数值偏小。经KMO 和巴特利球形检验分析，此案例数据量少，不适合做因子分析，这样就需要通过用其它方法来完成因子分析，如描述性统计表、共同性和旋转后成分矩阵等方法。

(2)描述统计表

描述统计表可显示各个变量的平均值和标准差，通过SPSS 数据分析软件的菜单功能生成(如表4)。在此表格中如果行列式为0，则说明可能在因子分析中存在计算问题，SPSS 软件就会发出警告信息或者无法完成因子分析。另外，变量水价的标准差为1.11490，是6 个变量中的最小标准差，这就意味着16 个德国城市的水价是最相似的。

表4 描述统计表

(3)共同性

共同性是一个变量与其他被考虑变量分享的方差集。表5 显示了每个可解释因子变量的方差比例。从表中可见，第二列每个变量方差的比例，即每个变量的初值都为1，这种提取方法是主成分分析法，所提取的值应该小于或者等于0。当值为0 时，表示非常不适合做因子分析，而这里的值都大于0。另外，第三列提取值表示丢失信息的百分比，如变量天然气价格提取值为0.843，相当于84.3%，约85%，代表这个变量中有15%的信息值丢失，共有85%的因素可以解释变量天然气价格，其它变量依此类推。

表5 共同性

(4)旋转后成分矩阵

旋转成分矩阵能够将结果更清晰地表达出来，在因子分析中运用旋转后成分矩阵非常重要，表6是因子模式矩阵，显示变量是如何加权给每个因子和变量的。表6 中的4 列数值是已提取的旋转因子，这4 个因子代表着变量间的相关性，取值范围在-1～+1 之间，值越接近1，做因子分析越有意义，通过因子间的比较人们可以决定每个变量归属于哪个因子。如“垃圾价”和“电价”在第一个因子下载荷度很高，分别为0.881 和0.780，“水价”和“天然气价”在第二个因子下载荷度高，分别为-0.918 和0.739，“道路清洗价格”在第三个因子下载荷度高，为-0.925，“地税”在第四个因子下载荷度高，为-0.879。根据6 个变量可知公共变量为价格，只有价格与人们的生活成本有关。第一个因子中因子得分最高的是垃圾价格和电价，说明这两个变量与人们生活息息相关，以此类推，地税与其他变量相比对人们的生活影响最小。因此，可将这4 个因子给出如下建议:因子1，与人们生活质量息息相关;因子2，与人们的生活密切相关;因子3，对人们的生活有影响;因子4，可能与人们生活有关联。

表6 旋转成份矩阵

2 结束语

本文介绍了通过SPSS 软件生成表格来进行因子分析，其前提条件是要做KMO 和巴特利特球形检验，当KMO 值超过0.6，同时巴特利特球形测试显著性不小于0.05，就可以做因子分析。此案例因数据库中样本量少，变量彼此相对独立，只能采用描述性统计、共同性和旋转后成分矩阵方法来完成因子分析，最终将6 个变量划分成为不同的因子，这些因子构成了与人们生活相关的几个方面。

［1］Jamie DeCoster，Overview of Factor Analysis，August 1，1998.

［2］Stevens，J.P.(1992).Applied Multivariate Statistics for the Social Sciences (2nd edition).

［3］Wegener，D.T.，＆ Fabrigar，L.R.(in press).Analysis and design for non experimental data:Addressing causal and non causal hypotheses.In R.T.Reis ＆ C.M.Judd(Eds.)，Handbook of research methods in social psychology.London:Cambridge University Press.

［4］王楠，苗迪.SPSS 因子分析在企业社会责任评价中的应用［J］.价值工程，2012(3):112-113.