路面结构中探地雷达传播精确高效数值模型

方宏远，李 健，钟燕辉，王复明

(1．郑州大学 水利与环境学院，河南 郑州450001;2．水利与交通基础设施安全防护河南省协同创新中心，河南 郑州450001)

0 引言

近年来，探地雷达凭借快速、连续、无破损等优点已经广泛应用于道路工程质量检测中． 精确测得路面结构各层材料的介电参数，是保证检测质量的关键之一． 获取材料介电参数的方法一般有两种:①检测法，即选取代表点钻芯取样，测试其介电参数，以检测结果作为一段距离内道路材料的介电参数，这种以点代面的方法不能反映整体路面材料介电特性;②反演方法，即基于探地雷达实测回波信号，利用优化算法反算路面结构层参数，这种方法检测精度高，广泛应用于探地雷达检测中．基于实测信号反演路面结构层参数的关键步骤之一就是建立探地雷达电磁波在路面结构层中传播的精确高效数值模型． 传统模拟探地雷达电磁波在地下结构中传播的方法有很多，主要包括传递矩阵方法［1］、射线追踪方法［2］、时域伪谱方法［3］、无网格方法［4］、时域有限差分方法(FDTD)［5］、ADI-FDTD 方法［6］等． 这些方法虽然都可以模拟探地雷达电磁波在层状结构中的传播，但也存在一些问题．比如传递矩阵方法对于有耗介质容易出现指数溢出问题，时域有限差分方法受到CFL 稳定条件的限制，计算效率受到制约，ADI-FDTD 方法虽然打破了CFL 条件的制约，但过大的时间步长会导致数值色散性显著增加．基于边值问题的精细积分方法是一种无条件稳定的高精度数值算法，其数值精度可以达到计算机意义上的解析解，且非常适合求解层状结构中波动问题［7-8］．笔者采用精细积分方法建立探地雷达电磁波在路面结构层中传播的数值模型． 并通过与FDTD 方法以及实测回波信号进行对比，验证笔者所建数值模型的精度和效率．

1 控制方程

探地雷达电磁波在层状结构中传播过程如图1 所示，发射天线向路面结构层发射电磁脉冲，电磁波在路面结构中遇到介质分界面发生反射和透射，反射波到达地表后由接收天线接收．探地雷达电磁波在层状结构中的传播过程满足Maxwell 方程组，由电磁场理论可知，二维各向同性介质中，频域TE 波方程可以表示为

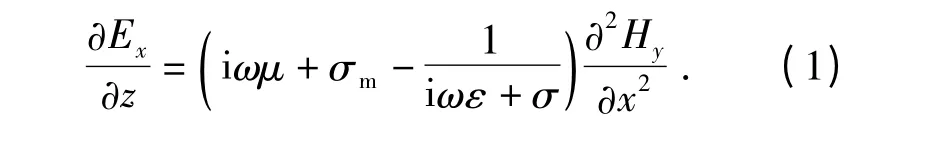
式中:H 表示磁场;E 表示电场;ε 表示介电常数;σ 表示电导率;σm表示导磁率;μ 表示磁导率;ω表示角频率;i 表示虚数单位．

平面问题中电场和磁场的频域列式可写为E(x，z)=E(z)·exp(ikx)． (3)H(x，z)=H(z)·exp(ikx)． (4)式中:k 表示波数．

将式(3)、(4)代入方程(1)、(2)中可得:

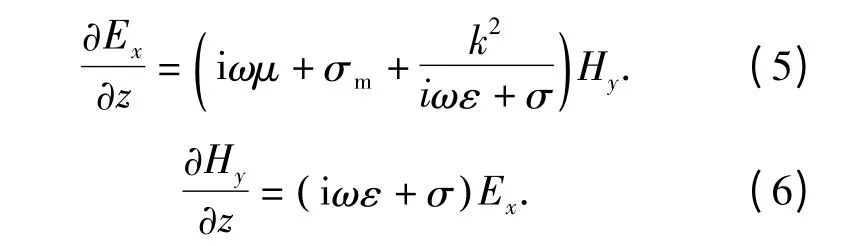
方程(5)和(6)可表示为

式中:v=［Ex，Hy］T;v'表示向量v 对z 的偏导数;T 为2 ×2 矩阵，矩阵元素为T11= T22=0，T12=σm+iωμ+k2/(iωε+σ)，T21=σ+iωε．

图1 层状结构中探地雷达电磁波传播示意图Fig．1 Diagram of GPR wave propagation in layered structure

2 基于边值问题的精细积分方法

对于线性系统，任意区间［za，zb］满足:

Eb=FEa-GHb． (8)

Ha=QEa+PHb． (9)

式中:Ea和Ha表示z =za处的电场和磁场;Eb和Hb表示z=zb处的电场和磁场，为方便描述，省略电场下标x 和磁场下标y;F，G，P 和Q 为待求的复数变量，其值仅与za和zb相关．

假设Ea和Ha已知，将方程(8)和(9)对zb求导可得:

E'b=F'Ea-G'Hb-GH'b; (10)

0 =Q'Ea +P'Hb +PH'b． (11)

zb端的控制方程可以表示为

E'b=T11Eb+T12Hb． (12)

H'b=T21Eb+T22Hb． (13)

联立方程(8)～(13)可得:

(F' -T11F-GT21F)Ea+(-G' -

T12-GT22+T11G+GT21G)Hb=0． (14)

(Q' +PT21F)Ea+(-PT21G+

P' +PT22)Hb=0． (15)

由于变量Ea和Hb是相互独立不相关的任意变量，方程(14)与(15)如果恒成立，那么Ea和Hb的系数必须为0，由此可得:

2．1 相邻区段方程的组装

对于区段［za，zb］和［zb，zc］，满足方程(8)和(9):

Eb=F1Ea-G1Hb; (17)

Ha=Q1Ea+P1Hb; (18)

Ec=F2Eb-G2Hc; (19)

Hb=Q2Eb+P2Hc． (20)

对于合并后的区段［za，zc］，也应满足方程(8)和(9):

Ec=FcEa-GcHc; (21)

Ha=QcEa+PcHc． (22)

联立方程(17)和(20)解得:

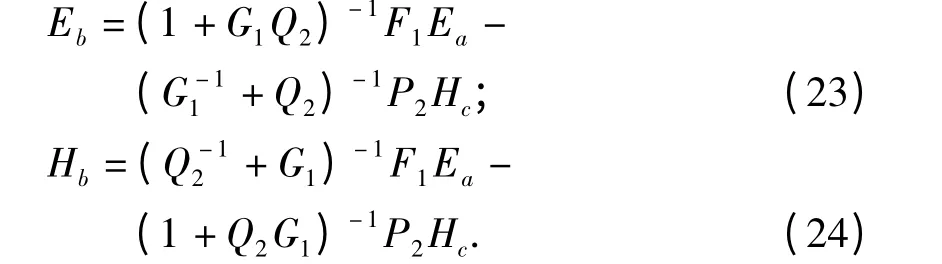
将方程(23)和(24)代入方程(18)和(21)整理可得:

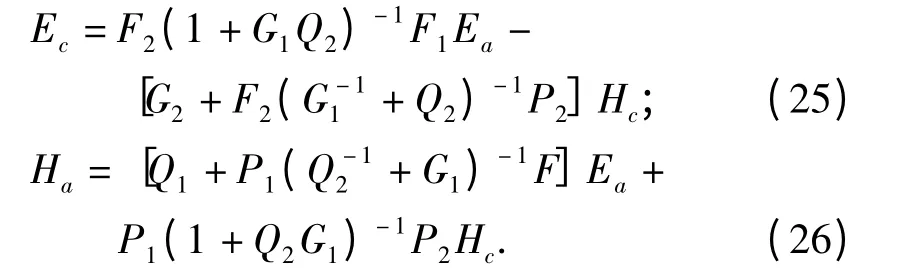
对比方程(19)、(20)和方程(25)、(26)左右端项可得区段变量合并方程组(27):

2．2 区段变量计算

方程(27)给出了由相邻区段［za，zb］和［zb，zc］区段变量F1，G1，P1，Q1和F2，G2，P2，Q2求解合并后区段［za，zc］区段变量Fc，Gc，Pc，Qc的方法，但是如何求解初始区段变量F1，G1，P1，Q1和F2，G2，P2，Q2仍然未知．

假设任意一层介质i，其厚度di=zi-zi-1，首先将其划分为2M(M 为正整数)等厚子层，厚度=di/2M，然后再将每个子层分为2N(N一般取20)等厚的微层，微层层厚t=dsubi/2N，由于此时层厚t 非常小，微层的区段变量F，G，P 和Q 可由泰勒级数展开求得

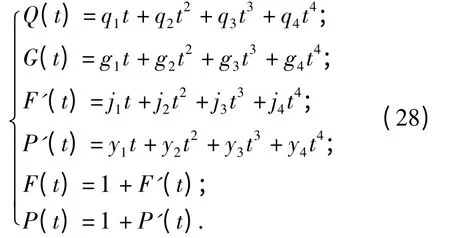
式中:qi，gi，ji，yi(i=1，2，3，4)为复数变量．

将方程(28)代入方程(16)对比各阶系数可得:

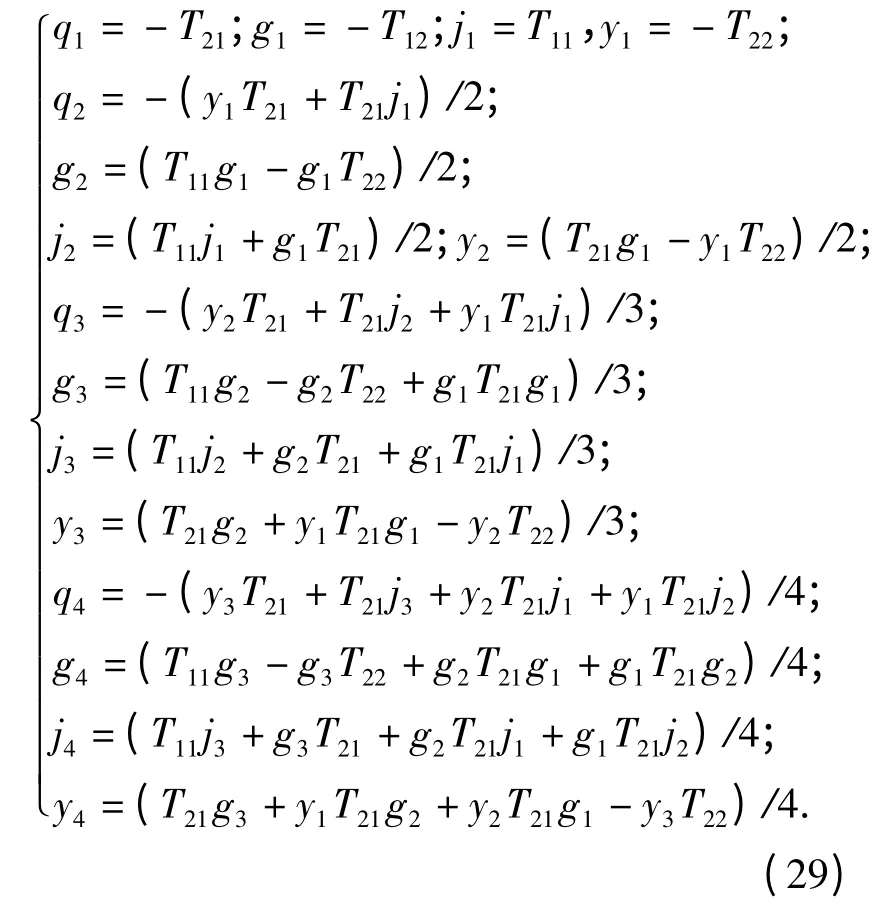
这里应注意，由于t 非常小，导致P'(t)和F'(t)非常小，由于计算机存在截断误差，直接将P'(t)和F'(t)与1 相加会导致精度损失殆尽，因此需对P'(t)和F'(t)进行单独储存计算，方程(30)为:

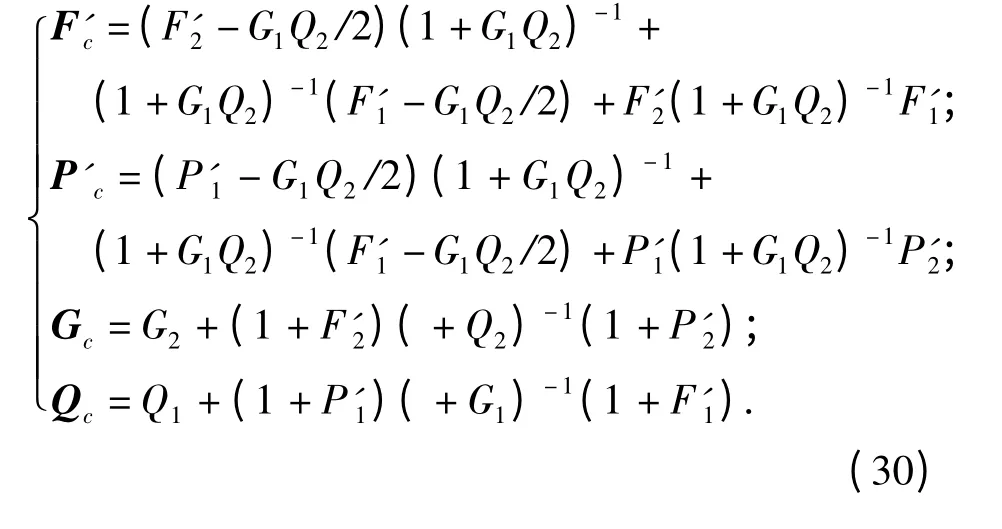
得到微层区段变量Ft，Gt，Pt和Qt后，利用方程(30)即可求出合并区段矩阵Fc，Gc，Pc和Qc，由于同一介质层内参数相同，所以每次合并后，层数会减少一半，经过N 次合并后即可得到子层的区段变量Fsub，Gsub，Psub和Qsub，然后利用子层区段变量合并求得层i 的区段变量Fi，Gi，Pi和Qi，这里需要说明的是，此时层厚已经不是一个很小的数，可以采用式(27)进行合并计算． 以此类推求得各层的区段矩阵，然后再利用式(27)合并得到整个n 层结构的区段变量Ftotal，Gtotal，Ptotal和Qtotal．

3 激励源设置与边界条件

3．1 激励源设置

设入射波源为第1 层介质和上半无限空间分界面处(z=z0)处电场和磁场的间断，即

式中:Em(k，ω)和Hm(k，ω)分别为电场和磁场的间断值．z+0表示z 轴正方向一侧z=z0界面，z-0表示z 轴负方向一侧z=z0界面．

3．2 上部边界条件

如图1 所示，n 层结构上部为半无限空间，其状态方程可以表示为:

式中:下标u 代表上半无限空间介质;Λu=diag(λu1，λu2)代表矩阵Tu的特征值矩阵;Mu=(αu1，αu2)代表相应特征向量矩阵;αui(i =1，2)为对应于特征值λui的特征向量．这里需注意特征值的排序，应保持第一行特征值λu1为正，对应于沿z 轴向上传播的波，第二行的特征值λu2为负，对应于沿z 轴向下传播的波．

设bu(z)=M-1u vu(z)，方程(32)可化为:

由一阶常微分方程理论可知，方程(33)的解可以表示为

bu(z)=exp［Λu(z-z0)］·bu(z0)，z ＞z0． (34)

其中bu(z0)是2 ×1 向量，第一行变量表示向上传播的波，第二行变量表示向下传播的波．对于上半无限空间来讲，不存在向下传播的波，即bu(z0)第二行为0，因此，

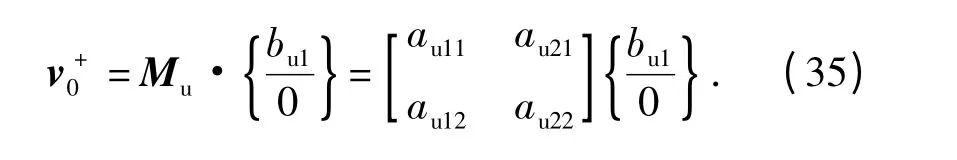
式中:下标0 代表向量v 在z =z0处的值，bu1代表bu(z0)中第一行元素． 联立求解方程(35)可得上半无限空间辐射边界条件:

3．3 下部边界条件

类似的下半无限空间的解可表示为

bd(z)=exp［Λd(zd-z)］·bd(zn)，z ＜zn． (37)式中:下标d 表示下半无限空间介质，由于下半无限空间中没有向上传播的波，即bd(zn)的第一行元素为0，即:

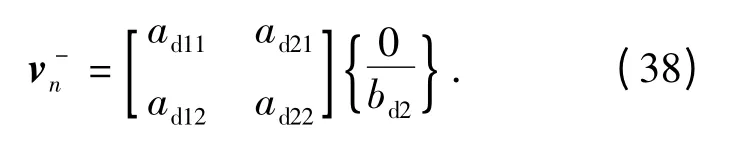
式中:下标n 代表向量v 在z =zn处的值，bd2代表bd(zn)中第二行元素．求解方程(38)，可得下半空间辐射边界条件:

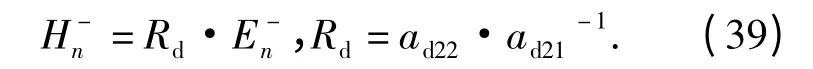
精细积分算法计算流程图如图2 所示．

图2 精细积分算法计算流程图Fig．2 Flow chat of PIM

4 数值算例

(1)单层结构反射系数． 通过一个单层结构来验证本算法的精度，设入射波方向与介质分界面垂直．即电场与磁场强度与波数k 不相关，那么方程(7)系统矩阵可简化为T11= T22=0，T12=σm+iωμ，T21=σ +iωε． 式(31)中电场和磁场的间断值可简化为Em(ω)和Hm(ω)．

设单层结构介质相对介电常数取9，电导率取0．02 s/m，上部半无限空间介质相对介电常数取1，电导率为0，下半无限空间介质相对介电常数取30，电导率取0．05 s/m． 所有介质磁导率都等于真空磁导率． 表1 给出了单层结构上表面处的反射系数，

由表1 可知，精细积分算法的计算精度与可以达到计算机意义上的解析解．

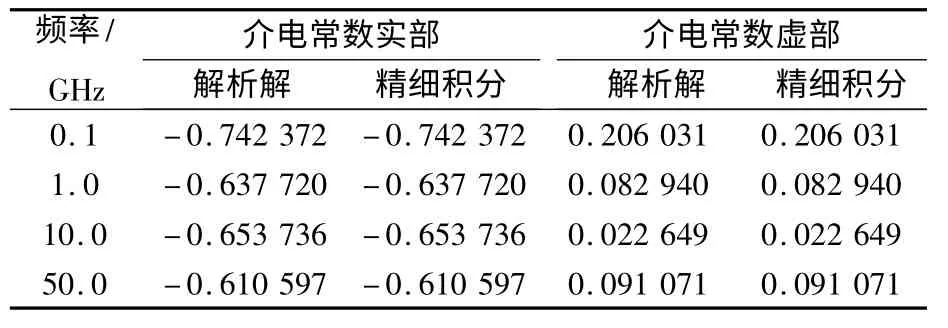
表1 单层结构反射系数计算结果Tab．1 Reflection coefficients of single layered structure

(2)四层半刚性路面结构． 表2 给出了四层半刚性路面结构介电参数取值(基于系统识别方法反演获得)． 图3 为时域入射波信号，由金属板反射试验获得．图4 和图5 分别给出了基于精细积分方法和FDTD 方法得到的模拟波形和实测波形的对比图．

表2 四层半刚性路面结构参数设置统计表Tab．2 Parameters of four-layer semi-rigid pavement

图3 入射波形Fig．3 Incident wave

由图4 和图5 可知，两种方法计算结果与实测波形基本吻合，但计算时间精细积分方法需要0．417 3 s，FDTD 方法需要0．589 5 s，精细积分方法计算效率比传统FDTD 方法高40%左右．

图4 精细积分方法模拟结果与实测波形对比图Fig．4 Comparison of the PIM and measured waveform

图5 时域有限差分方法模拟结果与实测波形对比图Fig．5 Comparison of FDTD and measured waveform

5 结论

笔者基于两端边值问题精细积分方法建立层状结构中探地雷达电磁波传播数值模型，该模型可以精确模拟探地雷达电磁波在层状结构中的传播过程．通过与路面实测探地雷达回波信号对比可知，模拟波形在波幅、时延等方面与实测波形吻合良好．此外，相比于传统时域有限差分方法，同等精度下，本算法可节省约40%的计算时间．

［1］ 郑宏兴，葛德彪． 广义传播矩阵法分析分层各向异性材料对电磁波的反射与透射［J］． 物理学报，2000，49(9):1702 -1706．

［2］ HUANG Yue-qin，ZHANG Jian-zhong，LIU Qinghuo． Three-dimensional GPR ray tracing based on wavefront expansion with irregular cells ［J］． IEEE Transaction on Geoscience and Remote Sensing，2011，49(2):679 -687．

［3］ FAN Guo-xing，LIU Qing-huo，HESTHAVEN J S．Multidomain pseudospectral time-domain simulations of scattering by objects buried in lossy media［J］． IEEE Transaction on Geoscience and Remote Sensing，2002，40(6):1366 -1373．

［4］ 冯德山，王洪华，戴前伟． 基于无单元Galerkin 法探地雷达正演模拟［J］． 地球物理学报，2013，56(1):298 -308．

［5］ IRVING J，KNIGHT R． Numerical modeling of ground penetrating radar in 2-D using MATLAB ［J］． Computers ＆ Geosicences，2005，32(9):1247 -1258．

［6］ FENG De-shan，DAI Qian-wei． GPR numerical simulation of full wave field based on UPML boundary condition of ADI - FDTD［J］． NDT ＆ E International，2011，44(6):495 -504．

［7］ ZHONG Wan-xie． Combined method for the solution of asymmetric Riccati differential equations ［J］． Computer Methods in Applied Mechanics and Engineering，2001，191(1/2):93 -102．

［8］ ZHONG Wan-xie，LIN Jia-hao，GAO Qiang． The precise computation for wave propagation in a stratified materials［J］． Journal for Numerical Methods in Engineering，2004，60:11 -25．