考虑站址误差的牛顿迭代定位算法

吴 昊，宁 勇

(中国航天科工集团8511研究所，江苏 南京 210007)

考虑站址误差的牛顿迭代定位算法

吴 昊，宁 勇

(中国航天科工集团8511研究所，江苏 南京 210007)

由于时差测量精度的提高，时差定位体制得到了广泛的应用。除量测误差外，站址误差也可能会对目标定位性能产生影响。提出了考虑站址误差的牛顿迭代方法，通过仿真实验分析了时差定位体制中TDOA量测误差及站址误差对定位性能的影响。

定位；时差；站址误差

0 引言

在现代测量技术条件下, 由于时差测量精度的提高, 时差定位体制得到了广泛的应用[1-3]。时差定位通常利用多站同时测量辐射源的方向或信号到达时间差( TDOA) 来完成，一个时差在空间上表现为双曲面，通过相交可得到目标位置。由于量测方程的伪线性，很多学者开展了相关的研究，经典方法为牛顿迭代算法和二步最小二乘法。

文献[2]的二次WLS算法指出目标定位精度对站址误差同样十分敏感。该算法在传统二次WLS算法的基础上考虑了站址误差，并给出一种考虑站址误差的TDOA定位算法，但是该算法在量测误差较大时，定位性能下降很快。本文针对量测误差较大的场景, 提出了一种考虑站址误差的牛顿迭代定位算法，具有更好的稳健性。首先给出了定位场景的数学模型，然后详细阐述了本文算法的流程，最后给出了算法的仿真分析。

1 数学模型

(1)

这里Δr服从均值为0、方差为Qr的高斯分布。

Qr=E[ΔrΔrT]

(2)

图1给出了时差定位的几何配置。

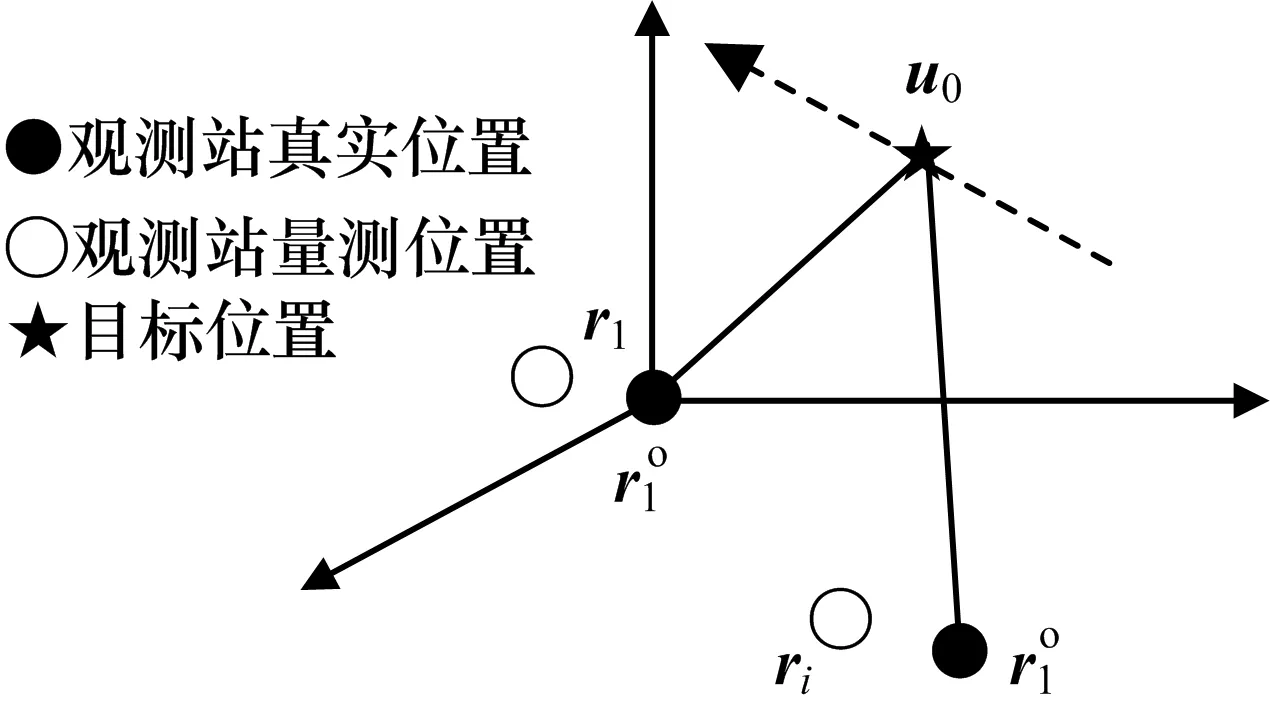
图1 时差定位的几何配置

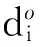
(3)

假设第一个站是主站，则观测站i与主站间的TDOA为：

(4)

这里为后面分析方便，将其转为到达距离差：

(5)

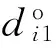
Qd=E[ΔdΔdT]

(6)

2 算法描述

2.1 牛顿迭代方法

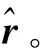
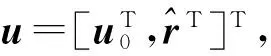
n=m-h(u)

(7)

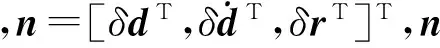
(8)

(9)

h(u(k-1))+H(u-u(k-1))≈m-n

(10)

式中，H为雅可比矩阵，记为：

(11)

式中,

令：

W=m-h(u(k-1))

(12)

以δu为未知变量，则：

e=W-H(u-u(k-1))=W-Hδu

(13)

利用最小二乘法可得：

δu=[HTQ-1H]-1HTQ-1W

(14)

因此第k次迭代的定位解u(k)可以通过式(15)更新为：

u(k)=u(k-1)+δu,k=1,2,…

(15)

初始迭代后的估计值u(1)一般误差较大，所以需要将它作为下次迭代的初值再次迭代计算获得新值，直到满足：

|u(k)-u(k-1)|<ε

(16)

时迭代停止，式中ε表示给定的门限。

2.2 初值获取

牛顿迭代过程是否收敛取决于初始坐标的选择[5]。它要求迭代运算的初始值必须接近真实值。本文通过间接求解法，针对三维环境下的目标，利用多个观测站位置，根据量测方程直接获得目标状态初值。

将式(3)代入式(5)，通过移项，平方，并将待估计量移到左边得：

(xi-x1)x+(yi-y1)y+(zi-z1)z=Pi-d1Δdi1

(17)

式中，

由于d1与u的非线性关系，上式实际是关于u的非线性方程，将它写成矩阵形式：

Au=B

(18)

式中，

此时假设d1已知，当观测站布站使得矩阵A满秩，可用伪逆法解方程组可得：

(19)

(20)

将其代入距离方程可得：

(21)

式中，

解方程可得：

d1=(-b±(b2-4ac)1/2)/(2a)

(22)

当d1为一正一负时,取d1>0的解，当d1的两解皆为正时, 则必须借助其它约束条件解定位模糊，若观测站个数大于3个，可以用冗余站点去模糊，否则可以考虑利用粗测向或者多普勒来排除虚假定位结果。

综上所述，本节算法流程如下：

3) 利用式(14)求得δu，并由式(15)更新u。

4) 若满足式(16)，则算法结束，否则返回步骤2)。

3 仿真分析

本节进行蒙特卡罗仿真试验，用于验证各种定位算法的有效性，设目标在(20,30,9)，单位为km，观测站个数为6，表1给出了真实站址。

表1 观测站真实站址

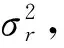
假设为0.1μs，图2给出了三种算法定位性能的比较。可以看出，当站址误差小于100m时，文献[2]算法和本文算法均近似于CRLB，并且效果好于Foy算法[4]。随着站址误差增大，文献[2]算法的定位结果开始发散，而本文算法仍然逼近CRLB。

图2 算法随σr变化的定位性能比较

图3 算法随σt变化的定位性能比较

为了比较TDOA量测误差对定位性能的影响，假设σr为20m，图3给出了两种算法定位性能的比较，当TDOA量测误差小于0.6μs时，两种算法定位性能

均近似CRLB，随着TDOA量测误差的增大，文献[2]算法开始发散，而本文算法仍接近CRLB。

从计算复杂度上分析，文献[2]算法仅需两次最小二乘处理，而本文算法在每次迭代均要一次最小二乘，计算量相对较大。

4 结束语

本文分析了TDOA量测误差、站址误差对定位精度的影响。给出了考虑站址误差的牛顿迭代定位方法。该算法定位精度较高，且定位精度对量测误差的敏感度小。■

[1] 朱伟强,黄培康,束锋,等. 多星TDOA和FDOA联合定位精度分析[J]. 系统工程与电子技术,2009,31(12)：2797-2800.

[2] Ho KC, Yang L. On the use of a calibration emitter for source localization in the presence of sensor position uncertainty[J]. IEEE Trans. on Signal Processing,2008,56(12):5758-5772.

[3] 郭福成，李腾. 基于时差和频差的固定多站定位方法及分析[J]. 系统工程与电子技术,2011(9):1954-1958.

[4] 王永诚,张令坤. 多站时差定位技术研究[J]. 现代雷达,2003(2):1-4.

A Newton Taylor series method for target localization with uncertain receiver positions

Wu Hao, Ning Yong

(No.8511 Research Institute of CASIC,Nanjing 210007，Jiangsu，China)

Target location system based on TDOA measurement is widely used because of the high precision. Beside of the TDOA measurement error, the receiver positions error has serious effect on the location accuracy. In the paper, the Newton Taylor series method considering the receiver position error is proposed. Numerical simulation shows the good performance of this algorithm.

target location；TDOA；receiver positions error

2014-11-18；2015-01-05修回。

吴昊(1984-)，男，工程师，博士，主要研究方向为电子对抗技术研究、数据处理。

TN97

A