钻孔体应变与面应变观测井孔耦合系数的计算

张凌空 牛安福

（中国北京100045中国地震台网中心）



钻孔体应变与面应变观测井孔耦合系数的计算

（中国北京100045中国地震台网中心）

钻孔应变观测系统（岩石、 膨胀水泥和应变仪钢筒）存在显著的井孔耦合效应， 只有确定这一耦合系数， 才能得到地壳岩石的真实应变值， 从而实现不同测点数据的可比性． 本文根据双衬套理论及弹性力学理论， 建立了三维空间应力作用下体应变与面应变观测力学模型， 并进一步推导各自井孔耦合系数计算式， 发现两组系数与井孔的受力状况密切相关， 分别与不同力源引起的应变信号相对应． 亦即应力比（钻孔轴向应力与平面应力之比）不同， 耦合系数也不一样， 体应变随应力比的增大而下降， 面应变则上升. 本文结果还表明平面应力作用下的耦合系数与外加应力无关， 只与观测系统本身有关， 故数值保持恒定. 此外， 文中对其影响因素也进行了分析， 结果表明， 体应变和面应变的井孔耦合系数均随岩石弹性模量和泊松系数的增大而增大， 且前者的幅度较大， 井孔耦合材料水泥对二者影响均很小．

体应变 面应变 井孔耦合系数 力学模型

引言

岩石、 膨胀水泥和仪器钢筒组成了3层复合双衬套结构， 由于应力集中和外加应力在各层介质中的连续传递， 井孔存在明显的耦合效应， 故测得的钻孔体应变（εTi）或面应变（εmi）不同于无孔岩石的真实体应变（εT）或面应变（εm）， 二者之间分别用体应变井孔耦合系数或面应变井孔耦合系数进行校正（即εTi=βTεT或εmi=βmεm）． 只有将观测应变值除以耦合系数才能得到地壳岩石的真实应变量（即εT=εTi/βT或εm=εmi/βm）， 从而各台站之间的数据才具有可比性， 这对于资料分析、 处理、 评估等具有实际意义．

钻孔应变仪问世以来很长一段时间, 观测台网一直发展缓慢（苏恺之等， 2003； 邱泽华， 石耀霖， 2004； 邱泽华， 2010）， 截止到2003年美国大约有25套体应变仪， 日本和中国各有30余套； 分量式应变仪使用得更少， 美国有4套， 日本和中国各约有8套， 所以井孔耦合系数问题一直很少有人探究． 开始于2003年的美国“板块边界观测计划（PBO）”（张宝红， 2004， 2010）， 决定沿圣安德烈斯断层和阿拉斯加南部地区新建175个钻孔应变观测台站， 目前已安装了85套Gladwin型分量式应变仪， 并获得初步观测资料（Roeloffs， 2010）． 受美国影响“十五”期间中国地震局进行了大规模数字化地震观测网络建设， 钻孔应变仪作为重要的形变前兆观测仪器在全国重点地震监测区得到使用和推广（欧阳祖熙等， 2009； 李海亮， 李宏， 2010； 牛安福等， 2011）， 其中国产TJ-2型体应变仪建立了近百个测点， 国产YRY-4型、 RZB-2和RZB-3型等分量式应变仪共建立了约60个测点， “十二五”期间有一大批台站启用．

新形势下钻孔应变观测台网的快速发展， 将井孔耦合系数的计算问题逐步推至议事日程． 早期， Evertson（1977）曾率先建立起三维空间应力作用下体应变的观测模型. 近年来张凌空等（2012）及张凌空和牛安福（2013）发现该模型在参数k的解算上有些问题， 便根据潘立宙（1981）、 欧阳祖熙和张宗润（1988）以及陈沅俊和杨修信（1990）先后提出的双衬套理论和弹性力学理论， 分别用两种方法重新解算了k值并得到相同结果． 本文以此工作为基础， 进一步推导体应变、 面应变观测井孔耦合系数的计算式， 并对各种影响因素进行分析．

1 三维空间应力作用下体应变与面应变观测的力学模型

世界上首台高灵敏度钻孔应变仪是美国华盛顿卡耐基研究所Sacks教授和德克萨斯大学Evertson博士于1968年共同研制成功的（刘澜波等， 1986）. 之后Evertson （1977）在“用于地震学研究的钻孔应变仪”的研究报告里， 首次建立了三维空间应力σ1,σ2,σ3作用下的钻孔体应变观测模型， 即

（1）

式中,E3和μ3分别表示岩石的弹性模量和泊松系数，k为探头钢筒内壁面应变与裸孔岩石面应变之比．

关于面应变计算， 分量式应变仪因为没有钻孔轴向上线应变记录功能， 故[σ3-μ3（σ1+σ2）]/E3一项可视为0， 因而探头记录到的面应变为

.

（2）

式（1）、 （2）中k是一个至关重要的参数， 它直接影响到模型的表述正确与否． Evertson（1977）采用两层介质力学模型（岩石、 仪器钢筒）， 并作了两点假定解算出k≈0.9． 由于实际观测系统为3层介质， 故忽略了水泥层影响的两层介质模型不是很合理． 张凌空等（2012）及张凌空和牛安福（2013）用双衬套法（潘立宙， 1981； 欧阳祖熙， 张宗润， 1988； 陈沅俊， 杨修信， 1990）和厚壁圆筒方程法（杨绪灿， 金建三， 1987）分别重新解算了k值， 并得到一致结果.

（3）

式中X4是与观测系统各层材料的弹性参数和半径都有关的一个量， 为

（4）

其中，α1=（1+μ1）/E1,α2=（1+μ2）/E2,α3=（1+μ3）/E3,β1=（1-μ1）/E1,β2=（1-μ2）/E2,β3=（1-μ3）/E3. 式中：r1，r2分别为钢筒内、 外半径；r3为井孔半径， 钢筒、 水泥、 岩石的弹性模量和泊松比分别为E1和μ1，E2和μ2及E3和μ3．

由于k≈0.9是Evertson（1977）根据Sacks-Evertson体应变仪的参数解算出来的， 又采用了两层介质简化模型， 故岩石弹性参数（E3，μ3）的合理取值范围变得很窄， 并且不适用于其它型号应变仪（如国产TJ-2型体应变仪、 YRY-4型和RZB型分量式应变仪等）的计算， 而式（3）则是通用式．

式（1）、 （2）构成了钻孔体应变与面应变观测的理论基础， 只要给出任何影响地应变观测的应力解（σ1，σ2，σ3）， 就可以代入这两个公式建立相应的模型， 如应变固体潮、 应变气压波和应变地震波等． 当σ3=0时， 平面应力（σ1，σ2）作用下探头钢筒内壁上的体应变和面应变的表达式分别为

（5）

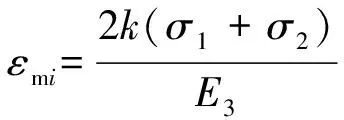
（6）

式（5）、 （6）与张凌空等（2012）根据双衬套理论推导的公式形式完全一致．

根据式（5）、 （6）也可以逆推回式（1）、 （2）， 即如果钻孔存在轴向主应力σ3， 则其对裸孔岩石产生的水平面应变为-2μ3σ3/E3， 对仪器钢筒内壁产生的面应变为-2kμ3σ3/E3， 沿钻孔轴向产生的线应变近似等于其周围岩体的轴向应变σ3/E3. 根据弹性力学中的叠加原理， 钢筒内壁径向应变和轴向应变等于每种外力单独作用下所产生的应变之和， 于是式（5）加上（1-2kμ3）σ3/E3， 式（6）加上-2kμ3σ3/E3， 就分别得到了在三维空间应力作用下的式（1）和式（2）．

在实际测量中体应变数据可由体应变仪直接给出， 面应变数值则需要简单求和. 对于国产四分量应变仪面应变等于两组相互垂直的分量元件数值之和， 国外三分量应变仪则等于3组测量元件数值之和的2/3．

2 三维空间应力作用下体应变与面应变的关系

将式（2）除以式（1）得

令η=σ3/（σ1+σ2）， 其物理含义是钻孔轴向应力与平面应力之比， 简称应力比， 则

（7）

f即为三维空间应力作用下体应变与面应变的转换系数， 有εmi=fεTi， 即体应变与面应变之间存在f倍的关系．

图1 三维空间应力作用下体应变与面应变的转换系数（f）随应力比（η）的变化

当观测系统的各项参数均为定值时， 如美国Sacks-Evertson体应变井（Evertson， 1977； 张凌空等， 2012），E1=19.6×1010Pa，μ1=0.30，r1=54 mm，r2=57 mm，r3=76 mm，E2=2.0×1010Pa，μ2=0.35. 取E3=5×1010Pa，μ3=0.25， 则f与η密切相关， 随其增大而减小（图1）． 当η值确定时f只与岩石的E3和μ3有关， 其变化规律与张凌空等（2012）给出的图2类似． 式（7）表明虽然体应变仪不能直接测得面应变， 但可以用公式将体应变转换成面应变． 当η=0时， 得到的是平面应力（σ3=0）作用下的转换系数

（8）

式（8）在张凌空等（2012）文中已作过比较详细的讨论．

3 无孔岩石的应变力学模型

根据弹性力学原理（杨绪灿， 金建三， 1987）， 在水平应力σ1，σ2和垂直应力σ3的作用下， 裸孔岩石的线应变为

其体应变为

（9）

面应变为

（10）

当σ3=0时得到平面应力作用下的力学模型为

（11）

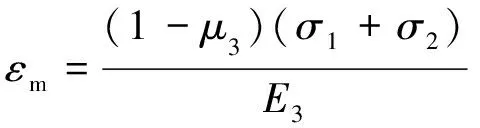
（12）

4 井孔耦合系数计算

4.1 三维空间应力作用下的井孔耦合系数

将式（1）除以式（9）， 得到体应变观测井孔耦合系数为

（13）

图2 三维空间应力作用下体应变与面应变井孔耦合系数（βT, βm）随应力比（η）的变化

将η=σ3/（σ1+σ2）代入式（13）得

（14）

同理， 将式（2）除以式（10）， 得到面应变观测井孔耦合系数为

（15）

图2给出了体应变、 面应变井孔耦合系数随应力比的变化. 可以看出，βT和βm与η密切相关， 当E3和μ3取定值时， 二者分别随η增加而下降或上升（图2）； 如果η、 钻孔和仪器等有关参数确定， 则二者只与岩石弹性模量和泊松系数相关（变化规律与图3相近）． 需要指出的是， 在不同的应力场中η值是不一样的， 如大气压、 地震波等． 因此， 在三维空间应力作用下耦合系数并非独立量， 而是与某种力源相对应， 同一口钻井可以有多个耦合系数； 数据标定也不具有普遍意义， 只是针对某种信号而言．

4.2 平面应力作用下的井孔耦合系数

通常情况下地壳岩石以水平应力为主， 在平面应力作用下，σ3=0，η=0， 根据式（14）和（15）有

（16）

（17）

这时耦合系数与外加应力无关， 对于特定的钻孔、 仪器， 只与岩石弹性模量和泊松系数有关． 表1给出了北京地区5个Sacks-Evertson体应变台站井孔耦合系数的计算结果．

表1 北京地区Sacks-Evertson体应变井的井孔耦合系数Table 1 Borehole coupling coefficient of Sacks-Evertson volume strainmeter in Beijing area

4.3 影响因素分析

“十五”以后我国使用的体应变仪主要是TJ-2型, 其技术参数为E1=21×1010Pa，μ1=0.30，r1=42 mm，r2=44.5 mm，r3=65 mm，E2=3.0×1010Pa，μ2=0.25 （苏恺之等， 2003）. 将其分别代入式（16）和（17）， 绘制出在平面应力作用下βT和βm随岩石弹性参数变化的曲线（图3）. 可以看出， 二者的变化规律很相近， 即二者均随岩石弹性模量和泊松系数的增大而增大， 只是体应变的幅值增大更多、 变化更剧烈． 由于应变仪探头安装时膨胀水泥的干稀程度每口井均会有一定的变化， 导致其弹性参数可能存在一定波动． 图4给出了βT和βm随E2和μ2的变化曲线. 可以看出， 在E2=2.1×1010Pa附近βT和βm达到峰值， 并且随μ2的增大而增大. 即当E2不变时，μ2每增加0.1，βT和βm分别平均增大

图3 体应变（a）、 面应变（b）井孔耦合系数与岩石弹性参数E3的关系

图4 膨胀水泥弹性参数μ2改变对体应变（a）与面应变（b）井孔耦合系数的影响

0.07和0.05； 当μ2不变时，βT和βm最大改变量分别为0.3和0.2． 一般情况下钻孔安装工艺要求E2控制在（2.5—4）×1010Pa范围内（苏恺之等， 1987）， 这样βT最多改变0.155，βm则为0.104. 因此E2和μ2的改变对体应变、 面应变的耦合系数影响很小．

5 讨论与结论

1） 在三维空间应力作用下钻孔体应变和面应变观测的力学模型可分别表述为式（1）、 （2）的形式， 其中参数k用式（3）表述. 该组公式构成了钻孔应变观测的一个理论基础， 只要给出任何影响地应变观测的应力解， 都可以代入这两个公式建立相应的模型． 由这两个公式还可以推导出体应变与面应变的转换系数， 从而实现了体应变观测数据向面应变观测数据的转换．

2） 井孔耦合系数（βT,βm）是指钻孔体应变或面应变的理论观测值与无孔岩石的理论真实值之比， 用以表明井孔耦合效应（由外加应力在各层介质中的传递引起）对观测的影响， 可分别表述为式（14）和（15）． 其中η=σ3/（σ1+σ2）， 为钻孔轴向应力与平面应力之比．βT随η增加而下降，βm则上升， 且βT变化幅度比βm小得多． 在平面应力作用下η=0，βT和βm均随E3和μ3的增加而上升， 且βT变化幅度大； 在工艺施工范围内（E2=（2.5—4）×1010Pa），E2和μ2改变对二者影响很小，βT最多减小0.155，βm最多减小0.104．

3） 通常情况下各测点体应变或面应变观测值一般不能直接进行比较（除非它们的观测条件完全相同）， 只有将实测值除以井孔耦合系数转换成真实的岩石应变值后， 各台站之间的数据才具有可比性， 这一步称作体应变或面应变观测的局地标定． 需要指出的是， 井孔耦合系数与井孔的受力状况有关， 在三维空间应力作用下（如大气压和地震应力等），βT和βm与η有关， 表明同一口井力源不同耦合系数也不一致， 因此标定值可以有多个； 在平面应力作用下（如日、 月潮汐引力）， 二者与外加应力无关， 只与观测系统本身有关， 因此耦合系数不变．

4） 本文使用的主要是Sacks-Evertson型和TJ-2型体应变井的技术参数， 对于其它型号的应变观测井情况与之类似， 只要将有关参数代入各公式同样可以计算和画图．

5） 本文从理论上探讨了应变仪观测与钻孔变形的关系， 这只限于很小的尺度. 由于地壳岩石横向不均匀性， 千米级乃至百千米级尺度范围内钻孔变形与周边地壳应变场的关系究竟如何， 是下一步需要重点关注的问题． 目前， 我国这方面深入细致的研究还很欠缺， 构造应变场测量中的有关理论与技术有待于进一步建立与提高．

研究过程中得到苏恺之和邱泽华研究员的大力支持与帮助， 在此谨表诚挚谢意．

陈沅俊， 杨修信. 1990. 双衬套钻孔应变测量的计算[J]. 华北地震科学， 8（4）: 80--89.

Chen Y J， Yang X X. 1990. Calculations of strain observation in the borehole with two cases[J].NorthChinaEarthquakeSciences， 8（4）: 80--89 （in Chinese）.

李海亮， 李宏. 2010. 钻孔应变观测现状与展望[J]. 地质学报， 84（6）: 895--900.

Li H L， Li H. 2010. Status and developments of borehole strain observations in China[J].ActaGeologicaSinica， 84（6）: 895--900 （in Chinese）.

刘澜波， 何世海， 宁长平， 刘北顺. 1986. Sacks-Evertson钻孔应变仪观测网在京津地区的安装[J]. 中国地震， 2（4）: 102--104.

Liu L B， He S H， Ning C P， Liu B S. 1986. Sacks-Evertson borehole strain cell network setting at Beijing-Tianjin area[J].EarthquakeResearchinChina， 2（4）: 102--104 （in Chinese）.

牛安福， 张凌空， 闫伟. 2011. 中国钻孔应变观测能力及在地震预报中的应用[J]. 大地测量与地球动力学， 31（2）: 48--52.

Niu A F， Zhang L K， Yan W. 2011. Borehole strain measurement and application to earthquake prediction in China[J].JournalofGeodesyandGeodynamics， 31（2）: 48--52 （in Chinese）.

欧阳祖熙， 张宗润. 1988. 钻孔应变仪与井壁耦合方法的研究[G]∥地壳构造与地壳应力文集（2）. 北京: 地震出版社: 1--10.

Ouyang Z X， Zhang Z R. 1988. Studies of method for coupling straingauge with borehole wall[G]∥CrustalTectonicandCrustalStress（2）. Beijing: Seismological Press: 1--10 （in Chinese）.

欧阳祖熙， 张均， 陈征， 李涛， 吴立恒， 师洁珊， 张宗润， 范国胜. 2009. 地壳形变深井综合观测技术的新进展[J]. 国际地震动态， （11）: 1--13.

Ouyang Z X， Zhang J， Chen Z， Li T， Wu L H， Shi J S， Zhang Z R， Fan G S. 2009. New progress in multi-component observation of crustal deformation in deep boreholes[J].RecentDevelopmentsinWorldSeismology， （11）: 1--13 （in Chinese）.

潘立宙. 1981. 与地应力测量有关的几个公式的推导和讨论[G]∥地应力测量原理与应用. 北京: 地质出版社: 163--202.

Pan L Z. 1981. On formulas of ground stress measurement[G]∥PrinciplesandApplicationofGroundStressMeasurement. Beijing: Geological Publishing House: 163--202 （in Chinese）.

邱泽华， 石耀霖. 2004. 国外钻孔应变观测的发展现状[J]. 地震学报， 26（增刊）: 162--168.

Qiu Z H， Shi Y L. 2004. Developments of borehole strain observation outside China[J].ActaSeismologicaSinica， 26（Suppl.）: 162--168 （in Chinese）.

邱泽华. 2010. 中国分量钻孔地应力-应变观测发展重要事件回顾[J]. 大地测量与地球动力学， 30（5）: 42--47.

Qiu Z H. 2010. A review of component borehole observation of stress-strain in China[J].JournalofGeodesyandGeodynamics， 30（5）: 42--47 （in Chinese）.

苏恺之， 刘瑞民， 裴玉珍， 张振声. 1987. 体积式钻孔应变仪与岩孔的耦合技术[G]∥地壳构造与地壳应力文集（1）. 北京: 地震出版社: 123--130.

Su K Z， Liu R M， Pei Y Z， Zhang Z S. 1987. The technique for coupling volumetric strainmeter to borehole[G]∥CrustalTectonicandCrustalStress（1）. Beijing: Seismological Press: 123--130 （in Chinese）.

苏恺之， 李海亮， 张均， 李秀环， 马相波. 2003. 钻孔地应变观测新进展[M]. 北京: 地震出版社: 1--56.

Su K Z， Li H L， Zhang J， Li X H， Ma X B. 2003.TheNewDevelopmentofBoreholeStrainObservation[M]. Beijing: Seismological Press: 1--56 （in Chinese）.

杨绪灿， 金建三. 1987. 弹性力学[M]. 北京: 高等教育出版社: 122--126.

Yang X C， Jin J S. 1987.Elasticity[M]. Beijing: Higher Education Press: 122--126 （in Chinese）.

张宝红. 2004. 美国的板块边界观测（PBO）计划[J]. 大地测量与地球动力学， 24（3）: 105--108.

Zhang B H. 2004. Plate boundary observation （PBO） project of USA[J].JournalofGeodesyandGeodynamics， 24（3）: 105--108 （in Chinese）.

张宝红. 2010. 美国板块边界观测（PBO）中的钻孔应变观测设备[J]. 大地测量与地球动力学， 30（增刊Ⅱ）: 40--44.

Zhang B H. 2010. Technical equipment for borehole strain-observation of PBO of USA[J].JournalofGeodesyandGeodynamics， 30（Suppl.Ⅱ）: 40--44 （in Chinese）.

张凌空， 牛安福， 吴利军. 2012. 地壳应变场观测中体应变与面应变转换系数的计算[J]. 地震学报， 34（4）: 476--486.

Zhang L K， Niu A F， Wu L J. 2012. Conversion factors from volume to area strain in crustal strain observation[J].ActaSeismologicaSinica， 34（4）: 476--486 （in Chinese）.

张凌空， 牛安福. 2013. 钻孔体应变与面应变观测参数k的计算[J]. 中国地震， 29（3）: 335--346.

Zhang L K， Niu A F. 2013. Calculation of borehole volumetric strain and area strain observation parameterk[J].EarthquakeResearchinChina， 29（3）: 335--346 （in Chinese）.

Evertson D W. 1977.BoreholeStrainmetersforSeismology，Rep.ARL-TR-77-62[R]. Audtin， Texas: Applied Research Lab， University of Texas: 1--144.

Roeloffs E. 2010. Tidal calibration of Plate Boundary Observatory borehole strainmeters: Roles of vertical and shear coupling[J].JGeophysRes， 115: B06405. doi:10.1029/2009JB006407.

Calculation of borehole coupling coefficient based on borehole volume strain and area strain observation

（ChinaEarthquakeNetworksCenter,Beijing100045,China）

Obvious borehole coupling effect exists in the borehole strain observation system （rock, expansive cement and strainmeter steel tube）.The real strain of rock in the crust can be obtained by determinng the coupling coefficient, so that comparativity of the data measured at the different points can be improved. According to the double bushing theory and elastic mechanics model, this paper establishes the mechanical models of volume strain and area strain observation under the action of three-dimensional stress. Then we deduced the borehole coupling coefficient formula at different observatories, from which we found that the coefficient was closely related to stress in the holes. The different strain signals can be correspondently attributed to different sources. That is to say, the stress ratio （the ratio of axial stress of drilling to plane stress） is different, the coupling coefficient is not the same. The volume strain decreased with the stress ratio increasing, and area strain increased. In addition, the coupling coefficients under plane stress had nothing to do with the additional stress, but only with the observation system as shown by the constant measurements. Finally, the affecting factors were analyzed. The results show that borehole coupling coefficient of volume strain and area strain increased with the rock elastic modulus and Poisson’s coefficient increasing, and the change in the former is larger, effect of borehole coupling material of cement on the two quantities is small.

volume strain； area strain； borehole coupling coefficient； mechanical model

10.11939/jass.2015.01.007.

国家科技支撑计划项目（2012BAK19B02-02）和地震行业科研专项（201108009）共同资助.

2014-03-03收到初稿， 2014-04-02决定采用修改稿.

e-mail: zhll1023@163.com

10.11939/jass.2015.01.007

P315.72+7

A

张凌空, 牛安福. 2015. 钻孔体应变与面应变观测井孔耦合系数的计算. 地震学报, 37（1）: 80--88.

Zhang L K, Niu A F. 2015. Calculation of borehole coupling coefficient based on borehole volume strain and area strain observation.ActaSeismologicaSinica, 37（1）: 80--88. doi:10.11939/jass.2015.01.007.