一类Hom-Hopf模基本定理

陶庭婷

一类Hom-Hopf模基本定理

陶庭婷

摘要:设L是一个三角Hopf代数. 通过表示范畴LM中Hom-Hopf代数的概念，证明了Hom-Hopf代数的对偶也是LM中的Hom-Hopf代数. 进一步给出了范畴LM中Hom-Hopf模的余不变子空间的定义并得到LM中的Hom-Hopf模基本定理.

关键词:Hom-Hopf代数；Hom-Hopf模；表示范畴

Hopf模基本定理[1]是Hopf代数理论的一个重要组成部分，即一个Hopf代数的Hopf模与其余不变子空间是Hopf模同构的，在Hopf代数的分类与表示理论中应用广泛. 1998年，Doi Y在Yetter-Drinfeld范畴中研究了Hopf代数与Hopf模的结构与性质，证明了辫子Hopf代数上的Hopf模基本定理，并通过Hopf代数的积分加以解释。2013年，王圣祥与郭双建[3]在余模范畴中研究了Hom-Hopf代数上的Hom-Hopf模基本定理.

Hom-Hopf代数的概念是由著名的代数学家Makhlouf A.和Silvestov S D[4-5]提出的，其中经典的代数结合律和余代数余结合律被一个自同态α扭曲. 后来，Donald Y[6-9]丰富了Hom代数的基本理论，提出了Hom模、Hom余模、Hom-Hopf模等概念. 2012年，Caenepeel S和Goyvaerts I[10]用范畴化的方法研究了Hom-Hopf代数和Hom-Hopf模.受此启发，人们就想在辫子张量范畴中研究 Hom-Hopf代数和Hom-Hopf模的结构与性质. 在文献[3]中，作者在余模范畴中得到了Hom-Hopf模基本定理. 一个很自然的想法，能否在模范畴中证明经典的Hom-Hopf模基本定理.

1基本概念

本文采用Sweedle[1]记法、概念和结论. 除非特别指出，讨论的向量空间均指域k上的向量空间，用⊗代替⊗k. 对于域k上的余代数C，记Δ:C→C⊗C，Δ(c)=c1⊗c2.

(1)表示范畴

设L是Hopf代数. 表示范畴LM中的对象是一个左L-模，态射是左L-模同态. 一个左L-模代数H是指对任意l∈L,h,k∈H有

l→(hk)=(l1→h)(l2→k),

l→1H=εL(l)1H.

可以看出，一个左L-模代数就是表示范畴中的一个代数. 类似地，可以定义一个左L-模余代数H：对任意l∈L,h∈H有

Δ(l→h)=(l1→h1)⊗(l2←h2),

εL(l→h)=εL(l)εH(h).

如果L是一个拟三角Hopf代数，那么表示范畴LM是一个辫子张量范畴，辫子为

C(m⊗n)=R2→n⊗R1→m,

m∈M∈LM,n∈N∈LM.

如果L是一个三角Hopf代数，那么表示范畴LM是一个辫子对称张量范畴.

(2)Hom-Hopf模

设(H,α)是Hom-Hopf-代数[5]，对线性空间M及M上的线性变换β，若存在线性映射ρ:M→M⊗H,φ:M⊗H→M使得(M,φ,β)为右H-Hom模，(M,ρ,β)为右H-Hom余模，且满足ρ(mh)=m(0)h(1)⊗m(1)h2，则称(M,β)为右H-Hom-Hopf模[8].

2主要结论及证明

定义1设L是一个三角Hopf代数. 表示范畴LM中的一个Hom-Hopf代数是指LM中的一个对象H，连同LM中的态射μ,η,Δ,ε,S,α，满足

(1)(H,μ,η,α)是一个Hom-代数，(H,Δ,ε,α)是一个Hom-余代数，

(2)μ,Δ,S与α可交换，

(3)Δ(hk)=h1(R2·k1)⊗(R1·h2)k2,Δ(1)=1⊗1,ε(hk)=ε(h)ε(k),ε(1H)=1k，

其中l∈L,h,k∈H.

引理1 设(H,μ,η,Δ,ε,S,α)是范畴LM中的一个有限维Hom-Hopf代数，那么它的对偶(H*,Δ*,ε*,μ*,η*,S*,α*)也是LM中的一个Hom-Hopf代数，其中η*=ε,ε*=η且

(Δ*(f⊗g))(h)=(f⊗g)(h1⊗h2)=f(R2·h1)g(S(R1)·h2)，

μ*(f)(h⊗k)=f(hk),α*(f)(h)=f(α(h)),S*(f)(h)=f(S(h)).

证因为H是一个有限维的Hom-Hopf代数，所以H*也是LM中的一个Hom-Hopf代数. 由LM的对称性容易验证H*满足定义1中的三个条件。

定义2设H是表示范畴LM中的一个Hom-Hopf代数，M称为LM中的一个右H- Hom-Hopf模，如果M既是一个右H-Hom模，又是一个右H-Hom余模，且满足

(1)ρM(mh)=m0(R2→h1)⊗(R1→m1)h2，(2)ρM(l→m)=(l1→m0)⊗(l2→m1)，

(3)l→(mh)=(l1→m)(l2→h)，

其中l∈L,h∈H,m∈M.

定理1设(H,α)是表示范畴LM中的一个Hom-Hopf代数，(M,β)是LM中的一个右H-Hom-Hopf模，则

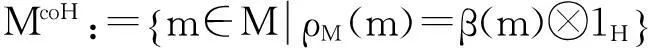
是一个L-子模，即McoH∈LM;

(2)设P(m)=β-4(m0)S(α-4(m1)),m∈M，则P(m)∈McoH;

(3)映射F:McoH⊗H→M,F(m⊗h)=mh是一个Hom-Hopf模同构.

证(1)设m∈McoH,l∈L，则有

ρM(l→m)=(l1→β(m))⊗(l2→1H)=(l1→β(m))⊗ε(l2)1H=β(l→m)⊗1H.

所以，l→m∈McoH，从而McoH∈LM.

(2)设m∈M,l∈L，则有

P(l→m)=β-4((l→m)(0))S(α-4((l→m)(1)))

=β-4(l1→m(0))S(α-4(l2→m(1)))，

l→P(m)=(l1→β-4(m(0)))(l2→S(α-4(m(1))))=β-4(l1→m(0))S(α-4(l2→m(1))).

所以，P是左L-线性的. 下证对任意m∈M，P(m)∈McoH. 事实上，

ρP(m)=ρ(β-4(m0)S(α-4(m1)))

=(β-4(m(0)))(0)(R2→(S(α-4(m(1))))1)⊗

(R1→(β-4(m(0)))(1))S(α-4(m(1))))2

=(β-4(m(0)))(0)(R2r2→S(α-4(m(1)2)))⊗

(R1→(β-4(m(0)))(1))(r1→S(α-4(m(1)1)))

=β-4(m(0)(0))(R2r2→S(α-4(m(1)2)))⊗

(R1→α-4(m(0)(1)))(r1→S(α-4(m(1)1)))

=β-3(m(0))(R2r2→S(α-5(m(1)22)))⊗

(R1→α-4(m(1)1))(r1→S(α-5(m(1)21)))

=β-3(m(0))(R2r2→S(α-4(m(1)2)))⊗

(R1→α-5(m(1)11))(r1→S(α-5(m(1)12)))

=β-3(m(0))(R2→S(α-4(m(1)2)))⊗

=β-3(m(0))(R2→S(α-4(m(1)2)))⊗

=β-3(m(0))(R2→S(α-4(m(1)2)))⊗

R1→(α-5(m(1)11)S(α-5(m(1)12)))

=β-3(m(0))(R2→S(α-4(m(1)2)))⊗R1→(ε(m(1)1)1H)

=β-3(m(0))(R2→S(α-3(m(1))))⊗ε(R1)1H

=β-3(m(0))S(α-3(m(1)))⊗1H

=β(P(m))⊗1H.

(3)定义G:M→McoH⊗H,g(m)=β-4(m(0)(0))S(α-4(m(0)(1)))⊗α-2(m(1)). 首先，对任意m∈McoH,h∈H,l∈L，有

l→F(m⊗h)=l→(mh)=(l1→m)(l2→h)，

F(l→(m⊗h))=F((l1→m)⊗(l2→h))

=(l1→m)(l2→h)，

所以，F∈LM. 类似地，可以证明G∈LM. 其次，我们证明FG=1M,GF=1McoH⊗H. 事实上，对任意m∈McoH,h∈H，有

ρM(mh)=m0(R2→h1)⊗(R1→m1)h2

=β(m)(R2→h1)⊗(R1→1H)h2

=β(m)(1L→h1)⊗α(h2)

=β(m)h1⊗α(h2).

从而，

GF(m⊗h)=G(mh)

=β-4((mh)(0)(0))S(α-4((mh)(0)(1)))⊗α-2((mh)(1))

=β-4((β(m)h1)(0))S(α-4((β(m)h1)(1)))⊗α-1(h2)

=β-4(β2(m)h11)S(α-4(α(h12)))⊗α-1(h2)

=(β-2(m)α-4(h11))S(α-3(h12))⊗α-1(h2)

=β-1(m)(α-4(h11)S(α-4(h12)))⊗α-1(h2)

=β-1(m)ε(h1)1H⊗α-1(h2)

=β-1(m)1H⊗h=m⊗h.

类似地，对任意n∈M，有

FG(m)=(β-4(m(0)(0))S(α-4(m(0)(1))))α-2(m(1))

=β-3(m(0)(0))(S(α-4(m(0)(1))))α-3(m(1)))

=β-2(m(0))(S(α-4(m(1)1)))α-4(m(1)2))

=β-2(m(0))ε(m(1))1H

=β-1(m)1H=m.

最后，我们证明F是一个Hom-Hopf模同态. 对任意m∈McoH,h,h′∈H，

F((m⊗h)h′)=F(β(m)⊗hα-1(h′))

=β(m)(hα-1(h′))=(mh)h′

=F(m⊗h)h′，

ρMF(m⊗h)=β(m)h1⊗α(h2)

=(F⊗idH)ρ(m⊗h).

证毕.

[参考文献]

[1]SWEEDLE M. E. Hopf algebras[M]. New York: Benjamin, 1969.

[2]DOI Y. Hopf modules in Yetter-Drinfeld categories[J]. Comm in Algebra, 1998, 26(9):3057-3070.

[3]王圣祥, 郭双建. 一类对称范畴上的Hom-Hopf模[J].山东大学学报(理学版) , 2013, 48(4):40-45.

[4]MAKHLOUF A, SILVESTO S. Hom-algebra structures[J]. J Gen Lie Theory, 2008, 3(2):51-64.

[5]MAKHLOUF A, SILVESTO S. Hom-algebras and Hom-coalgebras[J]. J Algebra Appl, 2010, 9(4): 553 - 589.

[6]YAU D. Enveloping algebras of Hom-Lie algebras[J]. J Gen Lie Theory, 2008, 2(2): 95-108.

[7]YAU D. Hom-algebras and homology [J]. J Gen Lie Theory, 2009,10(2):409 - 421.

[8]YAU D. Hom-bialgebras and comodule algebras [J]. Int Electron J Algebra, 2010,8(1): 45 - 64.

[9]YAU D. Hom-Yang-Baxter equation, Hom-Lie algebras, and quasitriangular bialgebras [J]. J Physics A: Math Theor, 2009,42(16): 165-202.

责任编辑：刘海涛

[10]CAENEPPEEL S, GOYVAERTS I. Monoidal Hom-Hopf Algebras[J]. Comm in Algebra. 2012, 40(6):1933-1950.

A Class of Fundamental Theorem of Hom-Hopf Modules

Tao Tingting

Abstract:Let be a triangular Hopf algebra. By using the definition of Hom-Hopf algebras in , the theorem that the dual of a Hom-Hopf algebra in is also a Hom-Hopf algebra was proved. Furthermore, the coinvariant subspace of a Hom-Hopf module was defined and the fundamental theorem of Hom-Hopf module in was obtained.

Key words:Hom-Hopf algebra; Hom-Hopf module; representative category

收稿日期：2014-11-12

基金项目：滁州学院科研启动基金项目(2014qd008)

作者简介：陶庭婷，滁州学院数学与金融学院教师，硕士，研究方向：Hopf代数及其表示理论(安徽 滁州 239000)。

中图分类号:O153

文献标识码：A

文章编号：1673-1794(2015)02-0017-04