图的2-赋权乘积顶点染色
2015-03-17张梅
张 梅
图的2-赋权乘积顶点染色
张梅
摘要:图G=(V,E)的k-赋权w是对图的每条边e∈E安排一个权值w(e)∈{1,2,…,k}.由边权导出图G的一个乘积顶点染色c,使得对图的每一个顶点v,c(v)(e)且对任意的边e=uv∈E,都有c(u)≠c(v). 本文研究了Kn-e,Pm×Pn(m,n≥2)和Pm×Cn(m≥2)2-赋权乘积顶点染色的存在性.
关键词:赋权;顶点染色; Cartesian积
1引言
本文研究的图均为简单连通图.设G=(V,E)是一个顶点集为V,边集为E的图. 图G的k-赋权w是对图的每条边e∈E安排一个权值w(e)∈{1,2,…,k}. 由边权导出图G的一个正常顶点染色c,如果对任意的边e=uv∈E,都有c(u)≠c(v),该染色通常称为k-赋权顶点染色. 显然,如果G≅K2,则G不存在任意的k-赋权顶点染色. 因此,下文中出现的图的顶点数均大于等于3. 和研究常见染色问题一样,我们更关心边赋权指标k最小的赋权顶点染色.

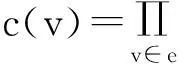
由于3可染色图G存在3-赋权加法顶点染色.人们自然也关心这样一类问题:是否二可染色(二部图)存在2-赋权加法顶点染色?哪些图类存在2-赋权加法顶点染色?
在2011年, Lu, Yu, Zhang等研究了可以2-赋权加法顶点染色的部分图类,证明了3联通二部图存在2-赋权顶点染色[8]. 最近,J. S. Kaziów 研究了2-赋权乘积顶点染色. 确定了部分可以2-赋权乘积顶点染色的图类[9].
下面介绍图的一种常见积运算[10]. 图G,H的Cartesian积,记为G×H,其顶点集和边集分别定义为:

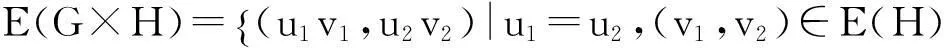
分别记n阶的路,圈和完全图为Pn,Cn和Kn.Kn-e表示完全图去掉任意一条边后得到的图.文中出现而未特别说明的术语记号可参考[11].
2主要结果
[7]中证明了Pn,Cn和Kn存在3-赋权乘积顶点染色. 我们证明了如下结论.
定理2.1(1)完全二部图Km,n存在2-赋权乘积顶点染色;
(2)Pn存在2-赋权乘积顶点染色当且仅当n≡2(mod4);
(3)Cn存在2-赋权乘积顶点染色当且仅当n≡0(mod4);
(4)Kn不存在2-赋权乘积顶点染色;
(5)Kn-e存在2-赋权乘积顶点染色.
证明(1)取Km,n任意一个顶点,将与之关联的边赋权值2,其余所有边赋权值1即可;
(2)注意到n≥6时,Pn存在2-赋权乘积顶点染色当且仅当Pn-4存在2-赋权乘积顶点染色.故我们只需考虑P2,P3,P4,P5四个图的2-赋权乘积顶点染色的存在性即可. 结论容易验证;
(3)注意到Cn存在2-赋权乘积顶点染色当且仅当边赋权值是序列1122的整数次循环,因此Cn存在2-赋权乘积顶点染色当且仅当n≡0(mod4);
(4)对Kn的每条边任意的赋权1或2,记该染色方案为c. 则n个顶点v1,v2,…,vn的染色集合为{c(v1),c(v2),…,c(vn)}⊆{1,2,22,…,2n-1},但是1和2n-1不可能在同一个染色集合中出现.因此必有两个顶点染一样的颜色,矛盾.
(5)记Ki+1-e是由Ki-e通过添加一个额外的顶点,并将之与原有顶点都连一条边得到的图,这里i∈{3,…,n-1}.注意到K3-e≅P3,由(2)可知它存在2-赋权乘积顶点染色,事实上它的两条边均赋权2.我们将依次得到Ki-e的2-赋权乘积顶点染色.首先将K4-e在K3-e边赋权的基础上对新增边全部赋权为1,容易验证这是一个K4-e的2-赋权乘积顶点染色.一般地,当i≡0(mod2)时,我们将Ki+1-e在Ki-e的边赋权基础上对新边全部赋权值2; 当i≡1(mod2)时,我们将Ki+1-e在Ki-e的边赋权基础上对新边全部赋权值1.注意到新增顶点的染色为1或者2i(取决于i的奇偶性),这与对应于Ki-e的原有顶点染色均不相同;同时原有顶点染色或者都保持不变或者都变为原来的2倍,因此我们得到Ki+1-e的2-赋权乘积顶点染色.
下面我们将主要考虑图的Cartesian积的2-赋权乘积顶点染色. 由Cartesian积定义可知对任意的图G,G×K1≅G.因此我们将主要研究Pm×Pn(m,n≥2)与Pm×Cn(m≥2)的2-赋权乘积顶点染色的存在性.我们先给出如下引理,该引理可参考文献[9],出于完整性考虑,我们写出它的证明.

证明不妨设V1={v1,v2,…,v2k}.由于G连通,存在vi到vi+k的路Pi,这里i∈{1,…,k}. 对图G的任意一条边e而言,如果所有的Pi包含e的次数和为奇数,则赋边权w(e)=2,否则赋边权w(e)=1. 则可以验证v∈V1时,有c(v)≡2(mod3),v∈V2时,c(v)≡1(mod3).这样就得到了G的一个2-赋权乘积顶点染色.
定理2.3Pm×Pn(m,n≥2)存在2-赋权乘积顶点染色.

最后,我们给出l为奇数时P2k+1×P2l的2-赋权乘积顶点染色. 记P2k+1:u1-u2-…-u2k+1,
P2l:v1-v2-…-v2l.我们给出P2k+1×P2l如下的边赋权方案w:
(1) 如果i≡1(mod2),则w(uivj,uivj+1)=1;如果i≡0(mod2),则w(uivj,uivj+1)=2,其中i∈{1,2,…,2k+1},j∈{1,2,…,2l-1}.
(2) 如果j≡1(mod2),则w(uivj,ui+1vj)=2;如果j≡0(mod2),则w(uivj,ui+1vj)=1,其中i∈{1,2,…,2k},j∈{1,2,…,2l}.
容易验证,这是P2k+1×P2l的一个2-赋权乘积顶点染色.
下面考虑Pm×Cn(m≥2)的2-赋权乘积顶点染色的存在性.事实上,由引理2.2和定理2.3,我们可以得出如下结果.
推论2.4当n≡0(mod2)时, Pm×Cn(m≥2)存在2-赋权乘积顶点染色.
证明设n=2l.如果m=2k,则Pm×Cn(m≥2)为二部图且每个部集的大小均为偶数,由引理2.2结论得证.如果m=2k+1,则在定理2.3的证明中对P2k+1×P2l的2-赋权乘积顶点染色基础上,对Pm×Cn(m≥2)未赋权边(uiv1,uiv2l)全部赋权值1,这里i∈{1,2,…,2k+1}.这样就得到了Pm×Cn(m≥2)的一个2-赋权乘积顶点染色.
注当n≡1(mod2)时, Pm×Cn(m≥2)是否存在2-赋权乘积顶点染色尚无一般性结论.不过容易验证当n=3时,P2×C3不存在2-赋权乘积顶点染色.
[参考文献]
[1]A. Frieze, R.J. Gould, M. Karonski, F. Pfender, On graph irregularity strength[J]. J. Graph Theory, 2002(41):120-137.
[2]M. Karnski, T. Luczak, A. Thomason, Edge weights and vertex colours[J]. J. Combin. Theory Ser. B, 2004(91):151-157.
[3]L. A.Berry, K. Dalal, C. M.Diarmid, B.A. Reed, A. Thomason, Vertex-colouring edge-wheitings[J]. Combinatorica, 2007(27):1-12.
[4]L. A. Berry, K. Dalal, B.A. Reed, Degree constrained subgraphs[J]. Discrete Appl. Math. 2008 (156):1168-1174.
[5]M. Kalkowski, M. Karoński, F. Pfender, Vertex-coloring edge-weightings: towards the 1-2-3-conjecture[J]. J. Combin. Theory Ser. B, 2010(100):347-349.
[6]J. S. Kaziów, 1, 2 Conjecture—the multiplicative version[J]. Information Processing Letters, 2008(107): 93-95.
[7]J. S. Kaziów, Multiplicative vertex-coloring weightings of graphs[J]. Information Processing Letters, 2012(112):191-194.
[8]H.L. Lu , Q.L. Yu, C.Q. Zhang, Vertex-coloring 2-edge-weighting of graphs[J]. European Journal of Combinatorics, 2011(32):21-27.
[9]J. S. Kaziów, Graphs with multiplicative vertex-coloring 2-edge-weightings[J]. to appear.
[10]W.Imrich ,S.Klavzar.Product graphs:Structure and Recognition[M]. Wiley-Interscience, New York,2000.
责任编辑:刘海涛
[11]A. Bondy, U.S.R. Murty,Graph Theory[M].Springer, London, 2008.
Multiplicative Vertex Coloring Edge 2-Weighting of Graphs
Zhang Mei
Abstract:Ak-weighting wof a graph G=(V,E)is an edge weighting assignment w(e)∈{1,2,…,k}for each edge e∈E. The weighting induces a multiplicative vertex coloring c, such that c(v)w(e) and c(u)≠c(v) for any edge e=uv∈E. In this paper, we mainly study the existence of proper multiplicative vertex coloring edge 2-weighting forKn-e,Pm×Pn(m,n≥2) and Pm×Cn(m≥2).
Key words:weighting; vertex coloring; Cartesian product
收稿日期:2014-11-09
基金项目:安徽省教育厅自然科学研究项目(KJ2013Z250); 滁州学院自然科学研究项目(2012kj001B); 滁州学院科研启动基金资助项目(2014qd010)
作者简介:张梅,滁州学院数学与金融学院讲师,研究方向:图论及其算法(安徽 滁州 239000)。
中图分类号:O157.5
文献标识码:A
文章编号:1673-1794(2015)02-0014-04
