基于最大m值法和恒应变速率法的Ti3Al基合金超塑变形行为研究
2015-03-17付明杰许慧元刘佳佳韩秀全
付明杰,许慧元,刘佳佳,韩秀全
(北京航空制造工程研究所 金属成形技术研究室,北京 100024)
基于最大m值法和恒应变速率法的Ti3Al基合金超塑变形行为研究
付明杰,许慧元,刘佳佳,韩秀全
(北京航空制造工程研究所 金属成形技术研究室,北京 100024)
分别采用最大m值法和恒应变速率法对Ti-24Al-15Nb-1.5Mo合金板材进行超塑拉伸,研究了940~1000℃、5.5×10-5~1.7×10-3s-1和不同拉伸轴方向的超塑性变形行为。结果表明:采用最大m值法获得的伸长率均高于恒应变速率法的,分别在980℃、垂直轧制方向获得了1596%的最大伸长率和960℃、3.3×10-4s-1、与轧制方向成45°获得了932%的伸长率。原始纤维组织经过超塑变形后发生等轴化,并且等轴晶粒随着应变速率的减小和温度的升高,长大程度逐渐增大。最大m值法超塑拉伸可以明显减少孔洞的产生。
Ti3Al板材;超塑性;晶粒等轴化;孔洞
随着航空发动机对材料要求的轻量化、耐高温的发展趋势,Ti3Al基合金具有优异的高温比强度、比刚度等特点,将是替代传统高温合金最有潜力的高温结构材料之一[1]。但是,其室温塑性差、成形困难及加工成本高等缺点限制了该合金的广泛应用[2]。然而,Ti3Al基合金却具有相对其他金属间化合物优异的超塑性[3],因此,超塑成形(Superplastic Forming, SPF)是解决该材料难加工成形的有效方法之一。20世纪90年代,各国学者对Ti3Al基合金超塑性做了大量工作,主要针对常规α2合金和Super-α2合金不同晶粒尺寸、α2和β含量以及变形参数对Ti3Al基合金的超塑性及超塑变形机制进行了研究[4-15]。最大m值法是通过控制超塑拉伸过程中的应变速率始终在与最大m值相对应的最佳应变速率附近循环变化,可有效获得材料的最高伸长率[16],本工作通过最大m值法和恒应变速率法研究Ti-24Al-15Nb-1.5Mo合金板材的超塑性,为其工程应用提供工艺参考。
1 实验材料及方法
1.1 实验材料
实验用Ti3Al基合金板材由北京航空材料研究院提供,厚度为1.5mm,名义化学成分为Ti-24Al-15Nb-1.5Mo。图1所示为该Ti3Al基合金板材的三维原始组织。可以看出,轧制方向和垂直轧制方向的α2相均以长条和细小等轴的形态组成,轧制面的α2相为大、小等轴晶混合形态,其中细小等轴α2相约2μm,α2相和β相的体积比Vα2∶Vβ约为60∶40。
1.2 实验方法
采用电火花线切割的方法加工出超塑拉伸试样的标距尺寸为10mm(长)×6mm(宽),其表面和侧面采用1200#水磨砂纸研磨。超塑拉伸试样的拉伸轴与板材轧制方向的角度分别选取为0°(L),45°和90°(T);拉伸温度为940~1000℃,温度间隔为20℃,恒应变速率法超塑拉伸的应变速率为5.5×10-5~1.7×10-3s-1。
超塑拉伸实验在CMT4104型微机控制电子万能试验机上进行,均热带长度为300mm,横梁移动速率在0.0001~500mm/min之间连续可调。最大m值法的拉伸速率增量ΔV为0.09mm/min,时间间隔Δt为6s。为了防止在高温变形时产生氧化,拉伸试样采用Ti-1200玻璃防护润滑剂保护。
试样拉断后立即水淬,保留试样的高温组织。采用BX41M金相显微镜和Quanta 250 FEG扫描电镜对拉断后试样的厚度方向进行微观组织观察。
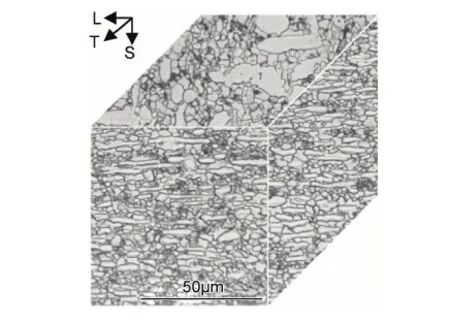
图1 Ti3Al板材的原始组织Fig.1 Primary microstructure of Ti3Al alloy sheet
2 结果与讨论
2.1 超塑拉伸伸长率
表1所示为恒应变速率和最大m值法的超塑拉伸伸长率结果。可见,采用恒应变速率法超塑拉伸的伸长率均低于1000%,最高伸长率在960℃、应变速率为3.3×10-4s-1、45°方向拉伸条件下为932%;而采用最大m值法超塑拉伸的伸长率几乎都超过1000%,在980℃和T方向拉伸条件下获得最高为1596%的伸长率。
2.2 恒应变速率法的应力-应变曲线
图2所示为L方向试样,应变速率分别在1.7×10-3s-1和5.5×10-5s-1条件下不同拉伸温度的应力-应变曲线,可以发现,应变速率为1.7×10-3s-1时,应力-应变曲线随温度的变化规律明显,随着温度的升高,相同应变条件下的应力减小,且随着应变的增加,应力逐渐减小。这是由于高应变速率条件下,变形机制主要由位错滑移控制变形,随着温度的升高位错的滑移能力增加,随着应变的增大,动态再结晶导致的软化效果更加明显,从而应力降低。当应变速率为5.5×10-5s-1时,与应变速率为1.7×10-3s-1的规律不同,当ε<1.35时,随着温度的升高,相同应变条件下的应力减小;然而,拉伸温度为960℃和980℃时,随着应变的增加,应力逐渐增加,拉伸温度为940℃时,流变应力对应变不敏感,动态应变硬化和软化达到平衡;当ε>1.35时,980℃变形时的应力反而高于960℃变形时的应力,随着温度的升高,低应变速率下晶粒容易长大,长大的程度也逐渐增加,晶界减少,而晶界滑移变得困难,从而触发晶内位错开动,导致应力随着应变增大,始终表现为加工硬化。
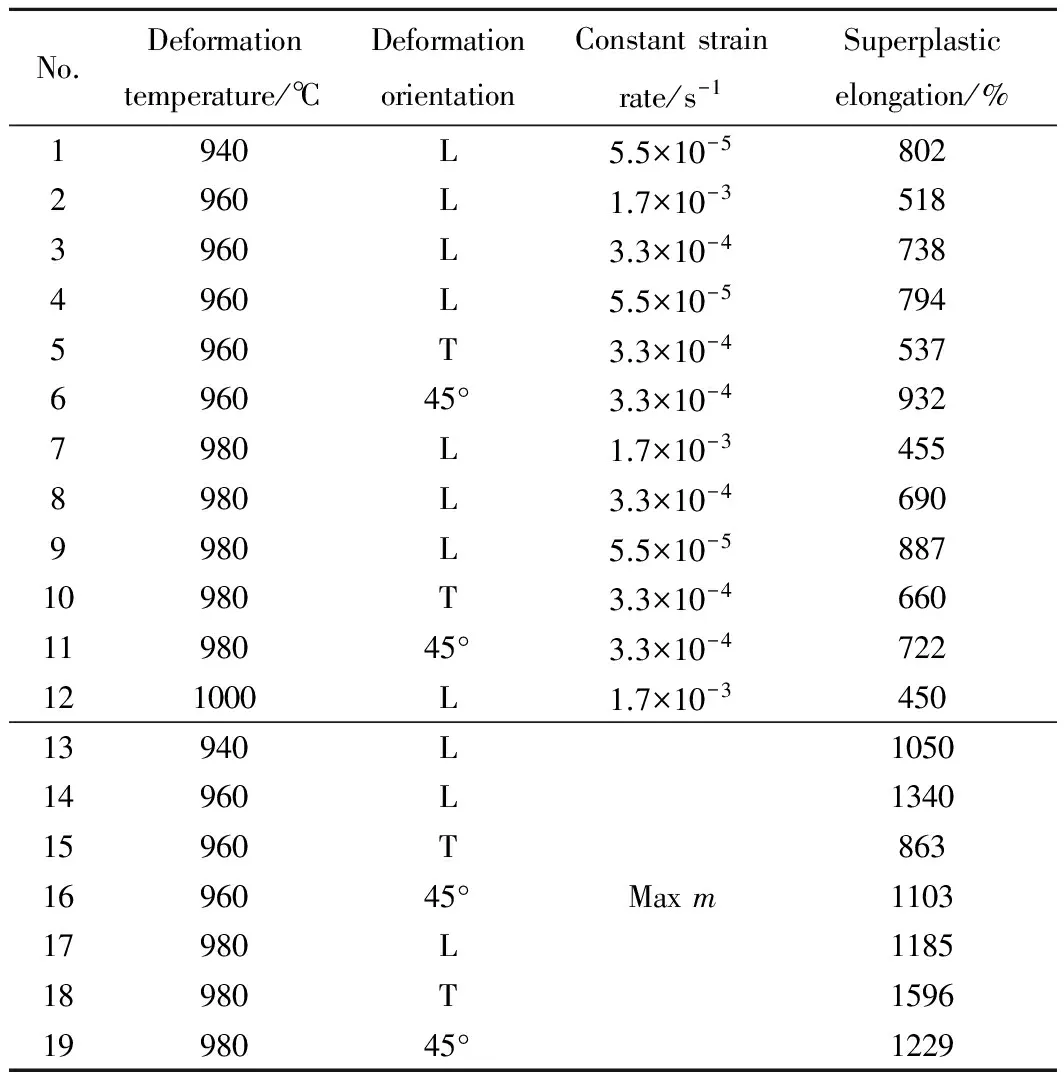
表1 恒应变速率和最大m值法下的超塑拉伸伸长率
对比相同拉伸温度、变形方向和不同应变速率的情况,如图3所示。可以发现,随着应变速率的降低,应力减小,伸长率增加,且应变速率≤3.3×10-4s-1时,应力随应变的变化平稳。
图4所示为恒应变速率条件下,变形方向对应力-应变曲线的影响。可以发现,960℃变形时,如图4(a)所示,45°方向的伸长率最大,T方向的最低,L方向居中,且三个方向的应力基本相当。这可能是由于45°方向具有最大的剪切应力,最容易使晶粒破碎,晶粒细化,从而晶界滑移更容易。在980℃变形时,如图4(b)所示,变形方向的影响不明显,应力和伸长率基本一致。
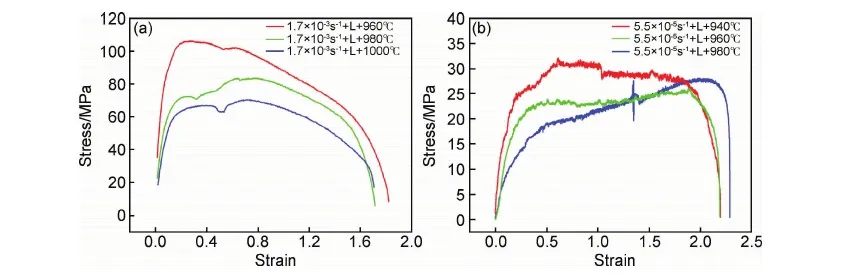
图2 温度对应力-应变曲线的影响 (a)1.7×10-3s-1;(b)5.5×10-5s-1Fig.2 Effect of temperature on the stress-strain curves (a)1.7×10-3s-1;(b)5.5×10-5s-1
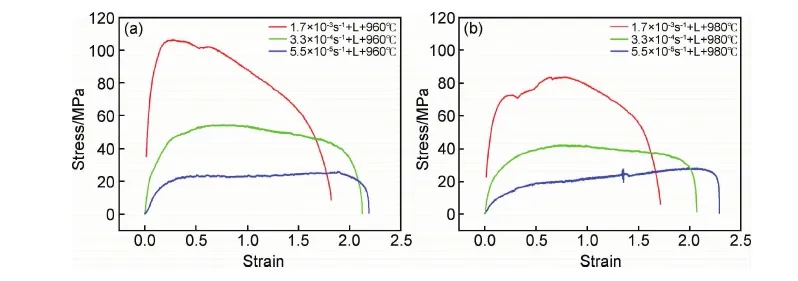
图3 应变速率对应力-应变曲线的影响 (a)960℃;(b)980℃Fig.3 Effect of strain rate on the stress-strain curves (a)960℃;(b)980℃
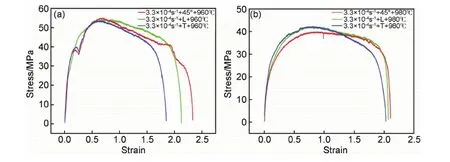
图4 变形方向对应力-应变曲线的影响 (a)960℃;(b)980℃Fig.4 Effect of load direction on the stress-strain curves (a)960℃;(b)980℃
2.3 最大m值法的应力-应变曲线
图5所示为最大m值条件下的应力-应变曲线。可以看出,960℃变形时,如图5(a)所示,L方向的伸长率最高,T方向的最低,45°方向居中,T方向的峰值应力最高,45°方向与L方向相当,随着应变的增加,流变应力差距减小;而在980℃变形时,如图5(b)所示,伸长率和流变应力基本相当;图5(c)为L方向不同温度的应力-应变曲线,960℃和980℃相当,而940℃时,随着应变的增加,应力先减小后增加。
图6所示为最大m值法拉伸过程中应变速率随应变的变化曲线。可以发现,所有条件下,应变速率均随着应变的增加而减小。这可能是由于超塑拉伸过程中应变速率的降低使得晶粒的变形协调机制具有足够的时间发挥到最大化,从而获得更高的伸长率。
2.4 微观组织
对比原始组织,可以看出,经过超塑变形后的组织最大的变化在于,原始的长条α2相完全消失,转变为等轴的α2相,图7所示为960℃、L方向、应变速率为3.3×10-4s-1的OM和SEM组织照片,其等轴化的α2相晶粒尺寸约为10μm,较原始的细小等轴α2相晶粒有所长大。Fu等[11]发现,随着应变的增加,条状α2相逐渐发生球化,且晶粒尺寸逐渐增大,并采用静态热处理的方法与之对比,发现静态热处理后晶粒十分稳定,条状α2相并未发生等轴化;Yang等[7]对应变诱发的Ti3Al合金超塑拉伸过程中α2相和β相的研究中发现,在低应变水平下,长条α2相断裂,形成等轴α2相是由于沿晶界表面发生剪切滑移。另外,有研究表明[17],对非等轴细晶的原始组织的TC4钛合金,利用预变形过程中产生的形变储存能,诱发TC4钛合金发生动态再结晶,获得细小等轴晶粒,从而提高材料的超塑性变形能力,获得了最佳预应变量为1.5和2147%的伸长率。可见,对于非细小等轴晶组织可以通过一定变形量的超塑变形得到改善,从而获得高的伸长率。

图5 最大m值条件下的应力-应变曲线 (a)960℃不同变形方向;(b)980℃不同变形方向;(c)L向不同变形温度Fig.5 The stress-strain curves of max m value method (a)960℃ with different tensile direction; (b)980℃ with different tensile direction;(c)tensile under L direction at different temperatures
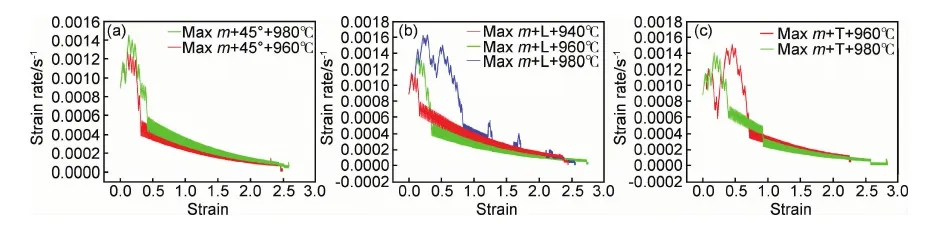
图6 最大m值法在相同变形方向不同温度的应变速率-应变曲线 (a)45°;(b)L;(c)TFig.6 The strain rate-strain curves of max m value method under same tensile direction at different temperatures (a)45°;(b)L;(c)T

图7 960℃+L+3.3×10-4s-1的变形等轴组织 (a)OM;(b)SEMFig.7 Microstructure under deformation parameter of 960℃+L+3.3×10-4s-1 (a)OM;(b)SEM
图8所示为980℃、L方向不同应变速率的显微组织。可见,随着应变速率的增加微观组织的晶粒尺寸减小,均匀性降低。应变速率为1.7×10-3s-1时,还保留原始组织的一些特征,长条晶粒,且960℃更为明显。
图9所示为960℃、3.3×10-4s-1不同变形方向的显微组织。可见,三个方向的微观组织在相同条件下差别很小。但是,980℃的组织晶粒尺寸均高于960℃的。
图10所示为不同变形条件下,断口截面的孔洞分布及形貌。可知,断口附近的微观组织不再呈等轴状,相对稳态变形区,其组织粗大,且α2相减少,各变形条件均有孔洞产生,其孔洞沿拉伸轴方向呈长条状,且连成一条线,长度约200μm,位置主要在试样截面的心部,如图10(a)所示;图10(b)所示为960℃,L,1.7×10-3s-1时,孔洞呈短条状,主要分布在截面中部,且分布不均,未连成长线状;而当应变速率为5.5×10-5s-1时,其孔洞形貌主要以点状存在,且分布在全截面上,且α2相仅占20%左右,如图10(c)所示;然而,从采用最大m值法拉伸断口可知,其心部无孔洞产生,且α2相并无显著减少,仅呈现粗化和拉长,如图10(d)所示。另外,还可以发现,在相同条件下,孔洞的形貌随应变速率的增加而从圆形点孔洞逐渐变为短长条型孔洞,如图10(b)和图11所示。这是由于孔洞的长大是由应力促进空位扩散和孔洞周围塑性变形机理相结合而促进孔洞长大的。在三角区处产生的应力集中由孔洞的产生而释放,在较高应变速率的条件下,释放后的晶界滑移尚不能进行充分协调变形,从而连续产生应力集中,进而形成长条形孔洞;而在较低的应变速率条件下,应力集中得到释放后,在较慢的变形速率下,变形协调机制可以充分发挥,从而抑制了孔洞的长大。

图8 980℃+L的应变速率对微观组织的影响 (a)5.5×10-5s-1;(b)3.3×10-4s-1;(c)1.7×10-3s-1Fig.8 Effect of strain rate on the microstructure at 980℃ and L direction (a)5.5×10-5s-1;(b)3.3×10-4s-1;(c)1.7×10-3s-1

图9 960℃+3.3×10-4s-1条件下变形方向对组织的影响 (a)L;(b)T;(c)45°Fig.9 Effect of load direction on the microstructure at 960℃ and 3.3×10-4s-1 (a)L;(b)T;(c)45°

图10 不同变形条件下的断口截面的孔洞分布及形貌 (a)960℃+45°+3.3×10-4s-1; (b)960℃+L+1.7×10-3s-1;(c)980℃+L+5.5×10-5s-1;(d)980℃+L+max mFig.10 Distribution of cavity on the fracture cross-section under different deformation parameters (a)960℃+45°+3.3×10-4s-1;(b)960℃+L+1.7×10-3s-1;(c)980℃+L+5.5×10-5s-1;(d)980℃+L+max m

图11 不同应变速率的孔洞形貌 (a)960℃+L+3.3×10-4s-1;(b)960℃+L+5.5×10-5s-1Fig.11 The feature of cavity with different deformation strain rate (a)960℃+L+3.3×10-4s-1;(b)960℃+L+5.5×10-5s-1
2.5 讨论
孔洞是超塑性变形过程中普遍存在的组织变化。在超塑变形达到一定程度,就会出现孔洞的形核,然后随着变形增加,孔洞长大,继而发生孔洞的聚合或连接,最终可能导致材料断裂。根据以往的研究报道[4-7]可知,高温条件下,有序的α2相表现为硬相,在β基体中自由滑动和转动,无序的β相则更趋于通过滑移和攀移进行协调。然而,当晶界滑动时界面上的粒子不会发生协调变形时,于是产生孔洞。Kim等[12]通过TEM观察发现局部位错发生在α2/α2晶界和α2/β相界处,而α2晶粒内部很少有位错产生,较软的β相发生剧烈变形,且位错主要堆积在晶粒三角区内,随着晶粒尺寸的增加,三角区应力集中增大,GBS更加困难,结果导致α2晶粒内的塑性变形,位错增加,而晶界无变形。从组织观察发现,由不同位置的点孔洞联结而成的短线孔洞在一条线上,最终再由短线孔洞联结成一条长线孔洞。
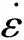
(1)
式中:Db是晶界扩散系数;Dp是晶界处颗粒直径;d是晶粒尺寸;Wb是晶界宽度;x是晶界滑动产生的应变占总应变的百分比;σ是流动应力;Ω是原子体积;kb是Boltzman常数;T是热力学温度。
3 结论
(1)采用恒应变速率法和最大m值法对Ti-24Al-15Nb-1.5Mo合金进行了超塑拉伸,最大m值法获得的伸长率均高于恒应变速率法,并在980℃、垂直轧制方向获得了1596%的最高伸长率。
(2)960℃变形时,变形方向对应力影响不大,对伸长率影响明显,45°方向的伸长率最大,T方向的最低,L方向居中;980℃变形时,变形方向的影响不明显,应力和伸长率基本一致。
(3)超塑拉伸过程中原始的纤维组织逐渐转变为等轴组织,随着应变速率的降低,等轴晶粒的长大程度增加。
(4)在相同条件下,孔洞的形貌随应变速率的增加而从圆形点孔洞逐渐变为短长条形孔洞。最大m值法超塑拉伸可有效减少孔洞的产生。
[1] 李世琼, 张建伟, 程云君, 等. Ti3Al和Ti2AlNb基金属间化合物结构材料研究发展现状[J].稀有金属材料与工程,2005,34(增刊3):104-109.
LI S Q, ZHANG J W, CHENG Y J, et al. Current status on development of Ti3Al and Ti2AlNb intermetallic structural materials[J]. Rare Metal Materials and Engineering, 2005,34(Suppl 3):104-109.
[2] 张建伟, 李世琼, 梁晓波, 等. Ti3Al和Ti2AlNb基合金的研究与应用[J]. 中国有色金属学报, 2010, 20(增刊1):336-341.
ZHANG J W, LI S Q, LIANG X B, et al. Research and application of Ti3Al and Ti2AlNb based alloys[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(Suppl 1):336-341.
[3] 杜兴蒿, 郭建亭, 周彼德. 单相组织金属间化合物的超塑性行为[J]. 钢铁研究学报, 2001, 13(6):52-55.
DU X H, GUO J T, ZHOU B D. Superplastic behavior of single-phase intermetallic compound[J]. Journal of Iron and Steel Research, 2001,13(6):52-55.
[4] ABHIJIT D, DIPANKAR B. Superplastic behaviour in a Ti3Al-Nb alloy[J]. Scripta Metallurgica, 1990,24:1319-1322.
[5] YANG H S, JIN P, MUKHERJEE A K. Superplastic behavior of regular α2and super α2titanium aluminides[J]. Materials Science and Engineering:A, 1992,153:457-464.
[6] YANG H S, JIN P, DALDER E, et al. Superplasticity in Ti3Al based alloy stabilized by Nb[J]. Scr Metall Mater, 1991,25:1223-1227.
[7] YANG H S, ZELIN M G, VALIEV R Z, et al. Strain induced morphological changes of α2and β phases in Ti3Al alloys during superplastic deformation[J]. Scripta Metallurgic, 1992,26:1707-1712.
[8] SPINGARN J R, NIX W D. Diffusional creep and diffusionally accommondated grain rearrangement[J]. Acta Metallurgica, 1998,26(9):1389-1398.
[9] PILLING J, RIDLEY N, ISLAM M F. On the modeling of diffusion bonding in materials: superplastic super alpha-2[J]. Materials Science and Engineering:A, 1996,205:72-78.
[10] IMAYEV R M, GABDULLIN N W, SALISHCHEV G A. Effect of grain size on superplasticity of an intermetallic Ti3Al compound[J]. Intermetallics, 1997,5(3):229-236.
[11] FU H C, HUANG J C, WANG T D, et al. Evolution of microstructure and superplastic deformation mechanism in super α2-Ti3Al base alloys[J]. Acta Mater, 1998, 46(2):465-479.
[12] KIM J H, PARK C G, HA T K, et al. Microscopic observation of superplastic deformation in a2-phase Ti3Al-Nb alloy[J]. Materials Science and Engineering:A, 1999,269:197-204.
[13] SALISHCHEV G A, IMAYEV R M, SENKOV O N, et al. Formation of a submicrocrystalline structure in TiAl and Ti3Al intermetallics by hot working[J]. Materials Science and Engineering:A, 2000,286:236-243.
[14] 刘莹莹, 姚泽坤, 罗茜, 等. Ti-24Al-15Nb-1.5Mo合金的超塑性能及超塑变形时的组织演化[J]. 稀有金属材料与工程, 2008,37(1):14-18.
LIU Y Y, YAO Z K, LUO X, et al. Superplastic properties and microstructural evolution during superplastic tension of Ti-24Al-15Nb-1.5Mo Alloy[J]. Rare Metal Materials and Engineering, 2008,37(1):14-18.
[15] 王旭, 曹京霞, 黄旭. Ti3Al基合金板材的超塑性研究[J]. 航空材料学报, 2012,32(1):20-24.
WANG X, CAO J X, HUANG X. Investigation on superplasticity of Ti3Al alloy sheet[J]. Journal of Aeronautical Materials, 2012,32(1):20-24.
[16] 王高潮,曹春晓,董洪波,等. TC11合金最大m值超塑变形机理研究[J]. 航空学报, 2009,20(2):357-361.
WANG G C , CAO C X, DONG H B, et al. Superplastic deformation mechanism of titanium alloy TC11 at maximummvalue[J].Acta Aeronautica et Astronautica Sinica,2009,20(2):357-361.
[17] 夏春林, 王高潮, 邓同生, 等. 基于最大m值法的TC4钛合金应变诱发超塑性变形工艺[J]. 机械工程材料, 2011,35(6):45-48.
XIA C L, WANG G C, DENG T S, et al. Strain-induced superplastic deformation process of TC4 titanium alloy based on maximummvalue method[J]. Materials for Mechanical Engineering, 2011,35(6):45-48.
[18] STOWELL M J, LIVESEY D W, RIDLEY N. Cavity coalescence in superplastic deformation[J]. Acta Metallurgica, 1984,32(1):35-42.
Superplastic Deformation Behavior of Ti3Al Based Alloy Based on MaximummValue and Constant Strain Rate Method
FU Ming-jie,XU Hui-yuan,LIU Jia-jia,HAN Xiu-quan
(Metal Forming Technology Department,Beijing Aeronautical Manufacturing Technology Research Institute,Beijing 100024,China)
The superplastic deformation behavior of Ti-24Al-15Nb-1.5Mo alloy with two different methods of based on maximummvalue and constant strain rate was studied over the range of 940-1000℃, 5.5×10-5-1.7×10-3s-1and different tensile axis direction. The result shows that the maximum superplastic elongation of maximummvalue is higher than that of the constant strain rate method, and 1596% and 932% are obtained, respectively, at 980℃, T direction and 960℃, 3.3×10-4s-1, 45° to rolling direction, respectively. The elongated grain of primary microstructure will be transformed to equiaxed grain during superplastic tension and the equiaxed grain size increases with decreasing of strain rate and increasing of deformation temperature. The maximummvalue method can obviously reduce the generation of cavities.
Ti3Al alloy sheet;superplasticity;equiaxed grain;cavity
10.11868/j.issn.1001-4381.2015.11.006
TG146
A
1001-4381(2015)11-0032-07
2014-05-10;
2014-12-18
付明杰(1981-),男,博士,高级工程师,主要从事高温钛合金、金属间化合物、高温合金的超塑成形/扩散连接工艺及基础理论研究工作,联系地址:北京市340信箱106分箱(100024),E-mail:fumj@bamtri.com
