可编程平面五连杆机械手

王子祺

一天我在网上看到一个“小贱钟”的视频，视频里的机械手能写出当前时间，但呈现的数字仅是一个可识别的状态，歪歪扭扭的非常不标准，有没有办法改变这一情况？

通过下载资料和结构图，我发现小贱钟其实是一个凸五连杆机械手的结构：两个舵机带动两个大臂运动，两个大臂再带动两个小臂，最后控制顶端的机械手做位移动作;加上两个舵机之间的间距，一共五个连杆。

目前，这种机械手还存在一定缺憾，只限于非实时、基于示教型的模式，只有先通过计算机记录人工走的轨迹，才能把该轨迹写出来。我的研究就是想解决这类机械手的实时性与可编程性的问题。

一、制作实物

采用SolidWorks三维实体设计软件设计平面五连杆机械手的每个零件;将这些零件在Solidworks中组装，进行虚拟仿真，对模拟过程中出现的问题进行修正与完善。当满足实验需求后，将零件图传给工厂。最后组装零件，形成实体结构平台。

二、优化选择，采集数据点

记录各点在X、Y坐标系下的转角数据。以平台的左下角为原点，建立平面直角坐标系，在横坐标上选择均匀分布的6个坐标点，在纵坐标上选择同样的5个坐标点，共30个抽样测试坐标点;通过编写测试软件，使之可通过两个电位计调整舵机脉冲信号的宽度（500μs至2500μs之间），从而以将近2000级的精度分别控制两个舵机，还可以把当前值显示在屏幕上。

利用这一原理，对每个取样坐标点进行人工定位，并记录每个坐标点对应的两个舵机的转角数值，共得到30对离散的X、Y坐标系上的数据样本。

三、处理数据

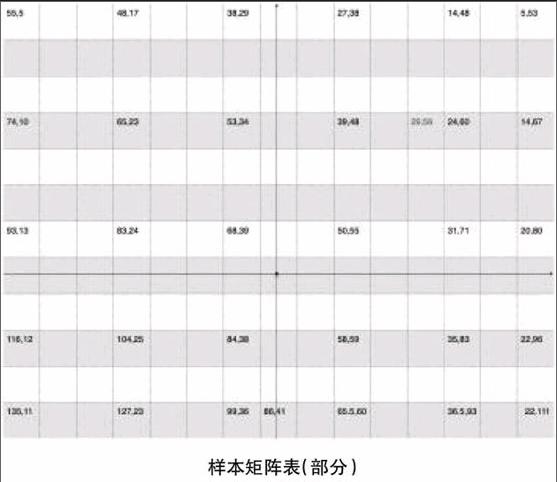
根据采集的坐标样本数据，得出矩阵表。将采集到的30对数据按列分成6组，并录入电脑（此时每组数据的x值不变），用Excel软件对每组数据中的两个舵机的角度值与y值进行高次方程多项式函数拟合，要求方程函数尽量满足采样点采得的数据（3次到5次多项式），再用R2值对其精度进行评价（R2值等于1时效果较好），找到左右两个舵机的角度值随y坐标的变化关系，最后得出6组、12个方程函数。

这时，以0.15（cm）作为y的增量（因为笔尖粗度为0.3cm），根据方程得到的函数算出这6列每一个x，y坐标点所对应的 α，β值。以行为组，用同样的方法算出能够覆盖整个平面的方程函数组，共55组，110个。

最后，以0.15（cm）作为x的增量，带入方程，求出与每一个（x，y）坐标对应的（α，β）值，再将所有数据整理到一起就得到一个x，y坐标平面的1.5mm坐标精度的75×55 的转角矩阵表。通过这个矩阵表，就可以为任何一个x，y坐标找到与它对应的α，β值了，从而达到精确控制舵机的目的。

四、书写实验

将一个数字带入矩阵表，对每个点采用逻辑与运算数学处理，在计算机中找到该数字的表达矩阵，连接矩阵中的各个相邻点就形成了笔的运动轨迹;按照从左到右，从上到下的顺序，形成书写的数据串;编写舵机控制程序，按照所生成的书写数据串逐点执行。

比如，从点（1.6，1.3）开始写，那么程序就会进行数学与运算，找到这个点所对应的微秒值组（1703μs，608μs），之后同时给两个舵机宽度为1703μs和宽度为608μs的脉冲信号，此时舵机带动两个大臂转到一个位置，通过公式算出这两个位置分别为距零位108.27°和距零位9.72° ，若想让机械手，也就是笔尖往右上方位移2.12mm到达点（1.75，1.15），程序会重新找到对应的微秒值组（1688μs，606μs），将之后的脉冲信号发给舵机完成位移，同理可求出此时两连杆距零位分别为106.92°和9.54°以及其他点的位移，最终在平台上得到书写笔迹。

通过以上技术路线可得到一个满足于对凸五连杆机械手进行控制的转置矩阵表。该方法的优点是克服了几何解析法的不足，及存在非线性和离散性不可克服的误差。

由于系统结构中每个连接点都可以活动，会有间隙，有可能造成一定误差。未来，我还将研究该系统的公差补偿方法，在每个点上做出补偿表，提高作业精度，将此结构与图像识别技术相结合，实现自动生成矩阵表。