动力翼伞多体非线性动力学建模与相对运动分析
2015-03-16陈自力张昊邱金刚
陈自力, 张昊, 邱金刚
(军械工程学院 无人机工程系, 河北 石家庄 050003)
动力翼伞多体非线性动力学建模与相对运动分析
陈自力, 张昊, 邱金刚
(军械工程学院 无人机工程系, 河北 石家庄 050003)
动力翼伞的监测与控制设备通常安装在负载上,而主要的气动力结构为翼伞,因此为了实现动力翼伞的精确控制,有必要对其两体相对运动进行分析。考虑动力翼伞的附加质量以及两点柔性连接的特殊结构,采用机理法建立了系统非线性八自由度(8-DOF)相对运动模型,包括翼伞六自由度与负载两体相对运动自由度。通过仿真,分析了动力翼伞在动力变化、转弯和雀降3种操纵下以及遇侧风干扰时的两体相对运动情况。结果表明,动力变化和雀降操纵会引起两体相对俯仰运动,而转弯与遇侧风时具有明显的相对偏航运动。研究结果表明,所建模型可用于解释与分析动力翼伞的两体相对运动问题。
动力翼伞; 两体; 附加质量; 相对运动; 侧风
0 引言
近年来,动力翼伞作为一种新型无人飞行系统,以其优秀的飞行性能和在侦察监视、物资投送等任务中的应用优势,已逐渐成为无人软翼飞行器领域的研究热点[1]。动力翼伞仅对传统滑翔伞的结构稍加改动,增加了以螺旋桨为主的动力装置,使之具有传统滑翔伞基本功能的同时,增加了高度与速度的可控性,以及姿态的灵活性,扩展了其应用空间。
目前,国内外已经提出了一些针对此类飞行系统的建模分析方法。文献[2-6]针对无动力的物伞系统分别采用机理法与安装分布式传感器的实验方法,建立了6-DOF刚体模型与7/9-DOF相对运动模型,分析了系统飞行过程中的相对偏航运动;文献[7-9]通过系统辨识,建立了物伞系统9-DOF模型,研究了单点连接条件下的三通道相对运动情况;文献[10]建立了动力翼伞纵平面模型,重点研究了动力变化时的系统纵向运动情况;文献[11-12]不考虑两体间的相对滚转运动,加入连接点处的摩擦力作用,建立了翼伞系统的非线性模型,研究了雀降过程的相对运动情况;文献[13]基于NASA X-38实验系统,通过可视化软件模拟系统飞行与降落过程,对相对运动进行了可视化分析;文献[14]所建立的模型中,伞绳扭转力矩是根据偏转后伞绳几何关系确定的,只适合特定结构的翼伞系统。相对于国外,国内对该领域的研究较少,只有文献[15]针对翼伞系统建立了6-DOF,8-DOF及12-DOF模型,研究了不同连接方式对相对运动的影响。综上所述,目前国内外的研究主要集中在针对物伞空投系统等无动力装置的建模与分析方面,而针对动力翼伞的建模与相对运动分析较少,这也是目前无法采取合理的非线性控制方法对动力翼伞进行准确、有效控制的主要原因之一。
本文考虑动力翼伞附加质量、两体相对运动与发动机推力,采用机理法建立动力翼伞8-DOF非线性相对运动模型,并在稳定滑翔初始状态下,对动力变化、转弯和雀降等操纵以及遇变向阵风时的两体相对运动情况进行了仿真分析,从而验证了模型的正确性与适用性。
1 相对运动模型
1.1 基本假设
针对动力翼伞的结构特点,在进行建模和分析前有必要对其做以下基本假设:(1)翼伞充满气后形状保持不变,除尾沿下偏外,可视为刚体,具有两个对称面;(2)翼伞与负载通过两组伞绳连接,共有两个连接点,飞行过程中绳的长度不变;(3)负载为旋成体且质量均匀,升力可忽略不计;(4)平面大地。
1.2 坐标系定义
为了准确描述模型的位置、速度和力学矢量,定义如图1所示的坐标系。
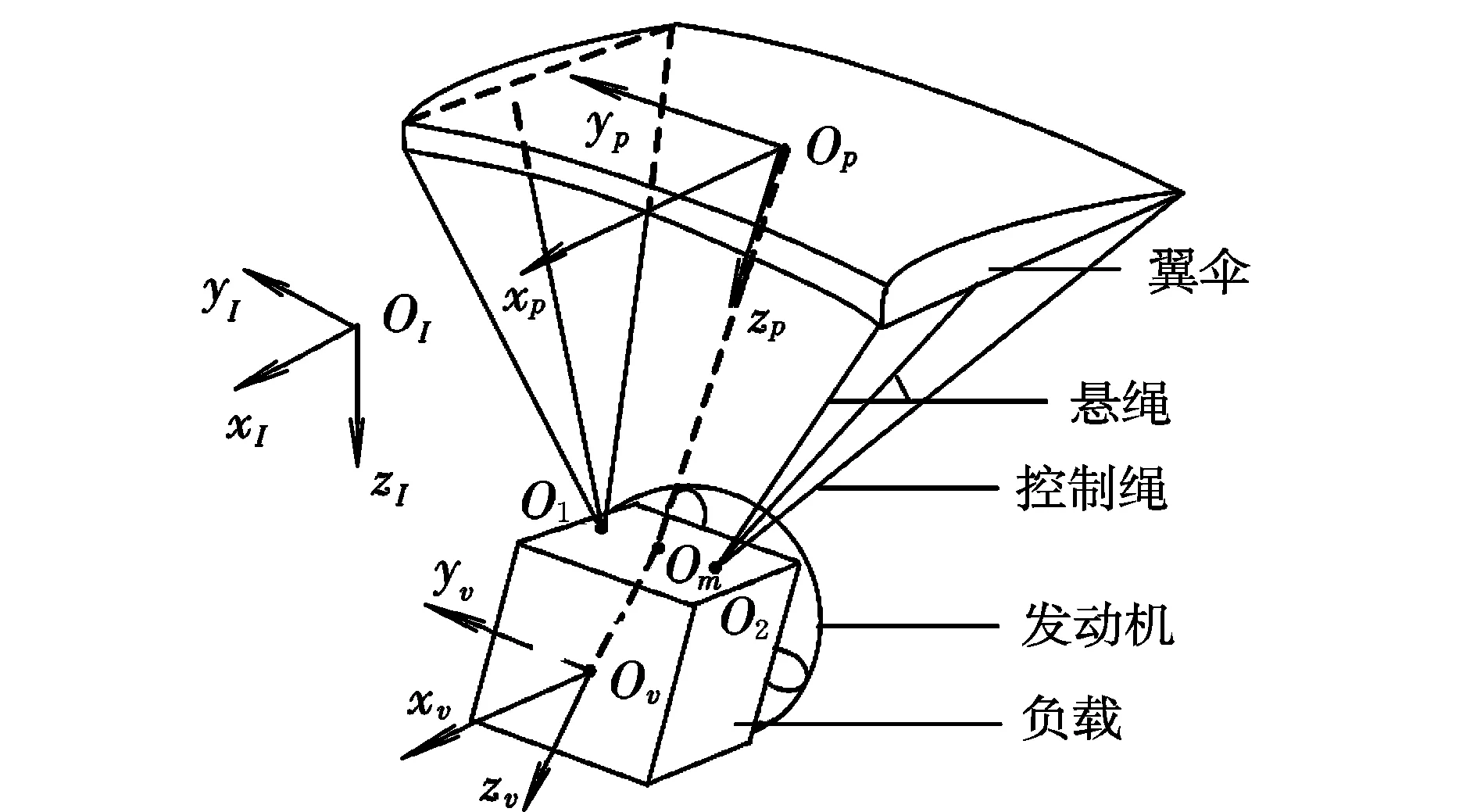
图1 坐标系定义Fig.1 Definition of coordinate system
(1)惯性坐标系OIxIyIzI。定义平面OIxIyI为水平面,zI轴正方向垂直水平面向下,符合右手法则,原点定义在地面。
(2)翼伞坐标系Opxpypzp。定义翼伞质心Op为原点,zp轴方向沿着原点Op指向悬绳与负载的交接点的中点Om,xp轴在对称平面内且与zp轴垂直,方向向前,yp轴垂直于Opzpxp平面符合右手法则。
(3)负载体坐标系Ovxvyvzv。定义负载质心Ov为原点,xv轴沿推力方向向前,zv轴在负载对称平面内且与xv轴垂直,方向向下,yv轴垂直于Ovzvxv平面符合右手法则。
惯性坐标系到翼伞坐标系的转换矩阵由翼伞的3个姿态角(φp,θp,ψp)定义:
TIp=
(1)
式中:s表示sin;c表示cos。
翼伞与负载的两点连接结构具有抑制相对滚转运动的作用,因此,在忽略伞绳形变时,可不考虑相对滚转运动[14]。负载坐标系到翼伞坐标系的转换矩阵可由负载相对于翼伞的姿态角(ψvp,θvp)定义:
(2)
1.3 动力学方程
1.3.1 翼伞力平衡方程
翼伞在飞行过程中的受力主要包括重力FpG、气动力FpA、惯性力FpI及伞绳拉力FpT,力的平衡方程为:
FpG+FpA+FpI+FpT=03×1
(3)
式(3)中的FpA包括基本气动力FpAR(升力和阻力)、附加质量产生的气动力FpAM及翼伞后缘下偏产生的气动力FpAδ,可表示为:
FpA=FpAR+FpAM+FpAδ
(4)
针对翼伞的展开椭圆形状与前后非对称特点,翼伞与内部气体产生的气动力采用Goodrick[16]提出的方法,将翼伞分为8片(见图2),分别计算各片气动力后进行等效叠加。
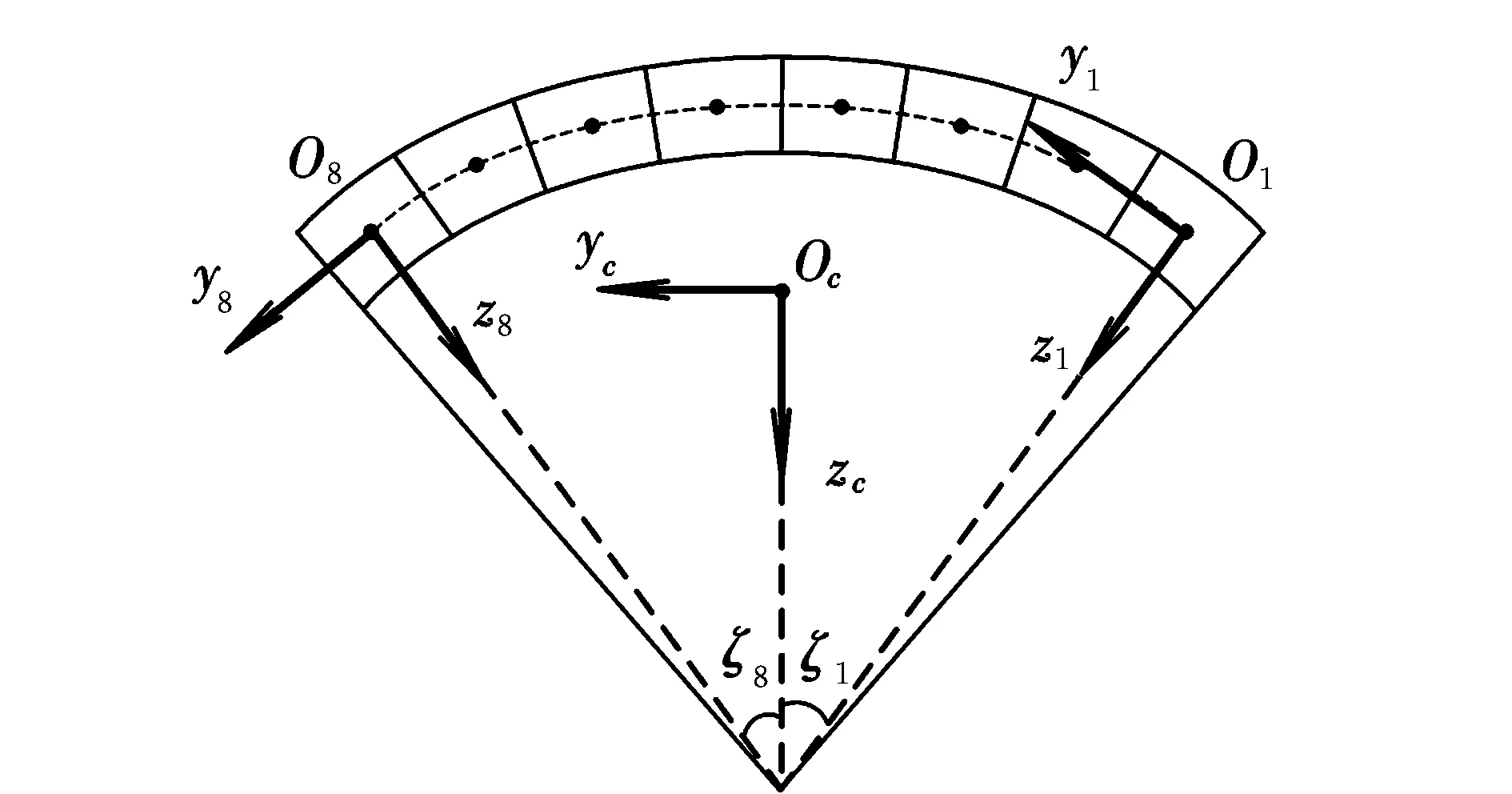
图2 气动力分片示意图Fig.2 The front view of segmentation of parafoil
各片的气动升力与阻力计算公式为:
(5)
(6)
式中:i=1,2,…,8为对应第i片的分量;ki为乘积因子(k1,k8=0.6;k2,k7=1.0;k3,k6=1.16;k4,k5=1.24);CLi和CDi分别为升力和阻力系数;ρ为大气密度;Sci为各片面积;uci,vci,wci为速度矢量在自身体坐标系下的分量。
翼伞整体的气动力叠加计算公式为:
(7)
式中:Ti-Oc为第i片自身坐标系与翼伞坐标系的变换矩阵,由伞绳与中轴线夹角ζi表示。
根据Barrows[17]提出的方法计算翼伞附加质量,定义ma为附加质量,则其产生的气动力为:
(8)
其中:
Vp=[upvpwp]T
1.3.2 翼伞力矩平衡方程
翼伞关于质心的力矩主要包括气动力矩MpA、惯性力矩MpI和拉力力矩MpT,重力作用于质心处,力矩为0,则翼伞力矩平衡方程为:
MpA+MpI+MpT=03×1
(9)
1.3.3 负载力平衡方程
负载所受的作用力主要包括气动力FvA、重力FvG、惯性力FvI、悬绳拉力FvT及发动机推力Fvth,平衡方程为:
FvA+FvG+FvI+FvT+Fvth=03×1
(10)
1.3.4 负载力矩平衡方程
负载关于质心的力矩包括气动力矩MvA、惯性力矩MvI及伞绳拉力力矩MvT,重力作用于负载质心,力矩为0,平衡条件下满足方程:
MvA+MvI+MvT=03×1
(11)
从翼伞与负载的作用力和力矩平衡方程中,消去悬绳拉力和拉力力矩,将式(3)及式(9)~式(11)联立可以得到动力翼伞的8-DOF相对运动模型,进而求解相对运动。
2 仿真结果及分析
根据上述机理法建立动力翼伞的相对运动仿真模型,以无外界干扰条件下的稳定飞行状态为初始状态,分别对动力变化、转弯和雀降3种操纵,以及遇变向阵风条件下的运动特性进行仿真分析。
小型动力翼伞结构参数如下:展长b=10.9 m,弦长c=2.8 m,翼伞面积Sp=30 m2,展弦比A=3.9,绳长l=6.2 m,翼伞质量mp=6.3 kg,负载质量mv=90 kg,负载等效面积Sv=0.75 m2。
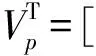
(1)动力变化响应
翼伞俯仰角和相对俯仰角变化如图3所示。

图3 翼伞俯仰角和相对俯仰角变化曲线Fig.3 Curves of pitch angle and relative pitch angle
计算结果表明,当Fvth=248.7 N时,动力翼伞可以保持稳定高度滑翔,此时为中动力。由图3可知,当动力变化时,翼伞俯仰角和相对俯仰角会出现明显的振荡和调整,且随着动力的增大,相对运动更剧烈。当达到最大动力Fvth=548.7 N时,相对俯仰角可达到17°,这将对飞行器姿态稳定性产生较大的影响。
(2)转弯操纵响应
图4为翼伞偏航角和相对偏航角变化曲线。由图4可知,在50 s时施加左侧下偏的转弯操纵,持续至110 s,动力翼伞处于滑翔状态时,偏航角和相对偏航角均为0°;施加操纵时,相对偏航角会出现剧烈振荡,衰减后依然大于0°,这也说明两体之间存在相对运动。
图5为两种下偏量条件下动力翼伞的飞行轨迹。由图5可知,盘旋半径与控制量成反比(下偏30%时半径为185 m,下偏50%时半径为110 m),且稳定性变差。在实际试验中发现,当控制量大于70%时,翼伞姿态变化过快,导致相对运动过于剧烈,致使飞行器失稳。因此,在实际操纵时,控制量应限制在小于50%的安全范围内。
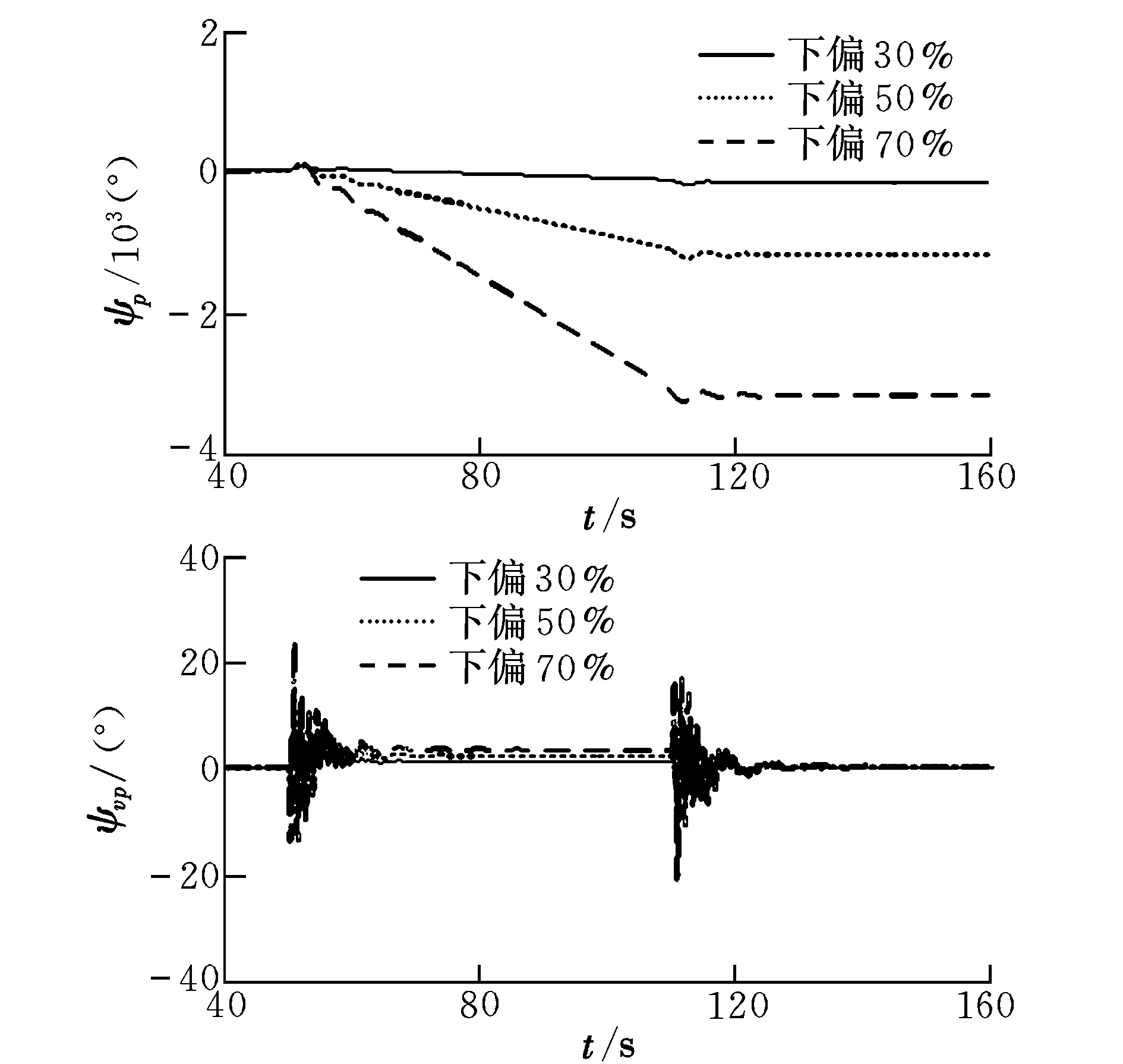
图4 翼伞偏航角和相对偏航角变化曲线Fig.4 Change curves of yaw angle and relative yaw angle
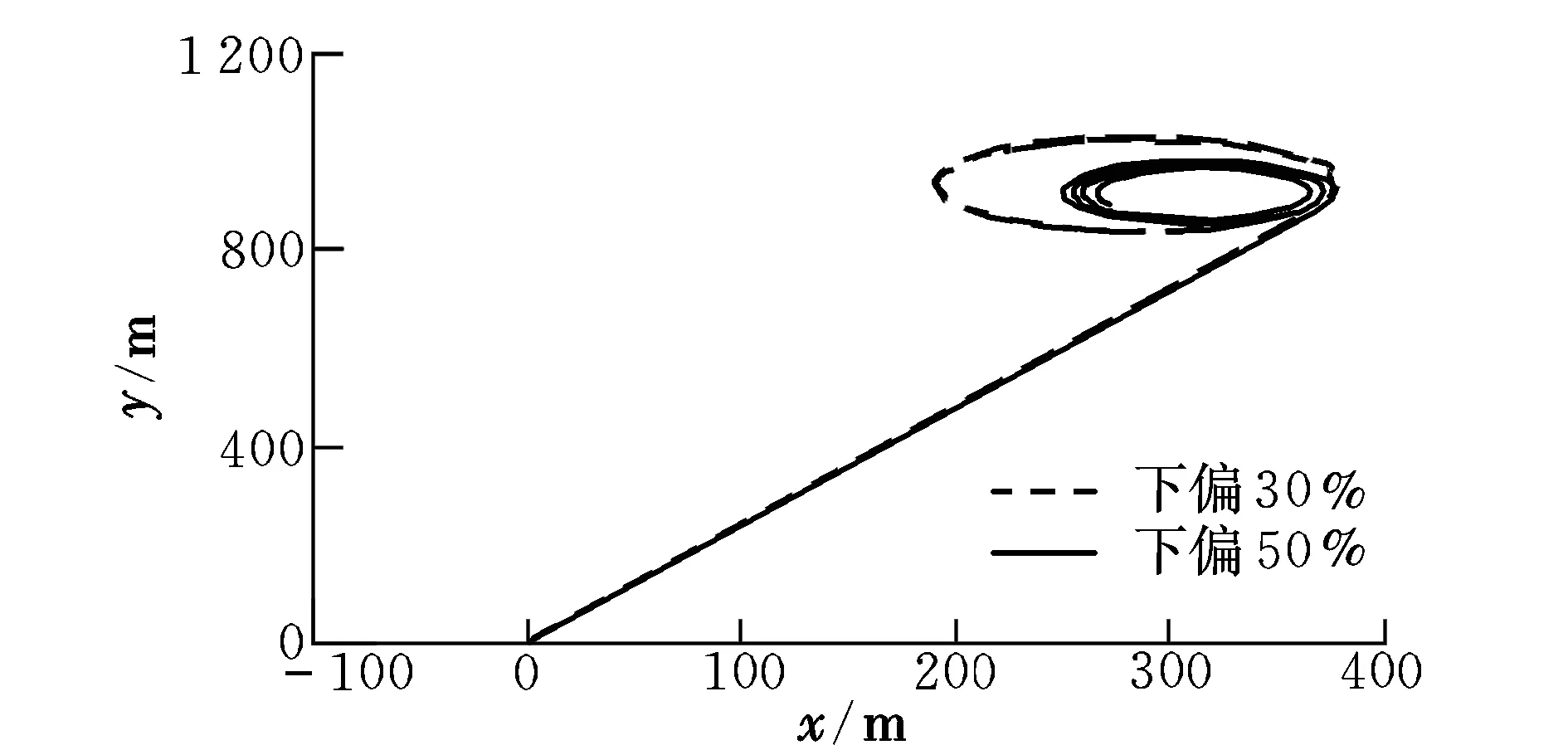
图5 不同下偏量时动力翼伞的飞行轨迹Fig.5 Trajectories under different downward deflection
(3)雀降操纵响应
雀降一般在距降落点一定距离时进行快速操纵,用于降低纵向速度,从而实现动力翼伞的“定点着陆”与“无损着陆”,或在紧急情况时,用于快速降低动力翼伞高度。图6为翼伞俯仰角和相对俯仰角变化曲线。
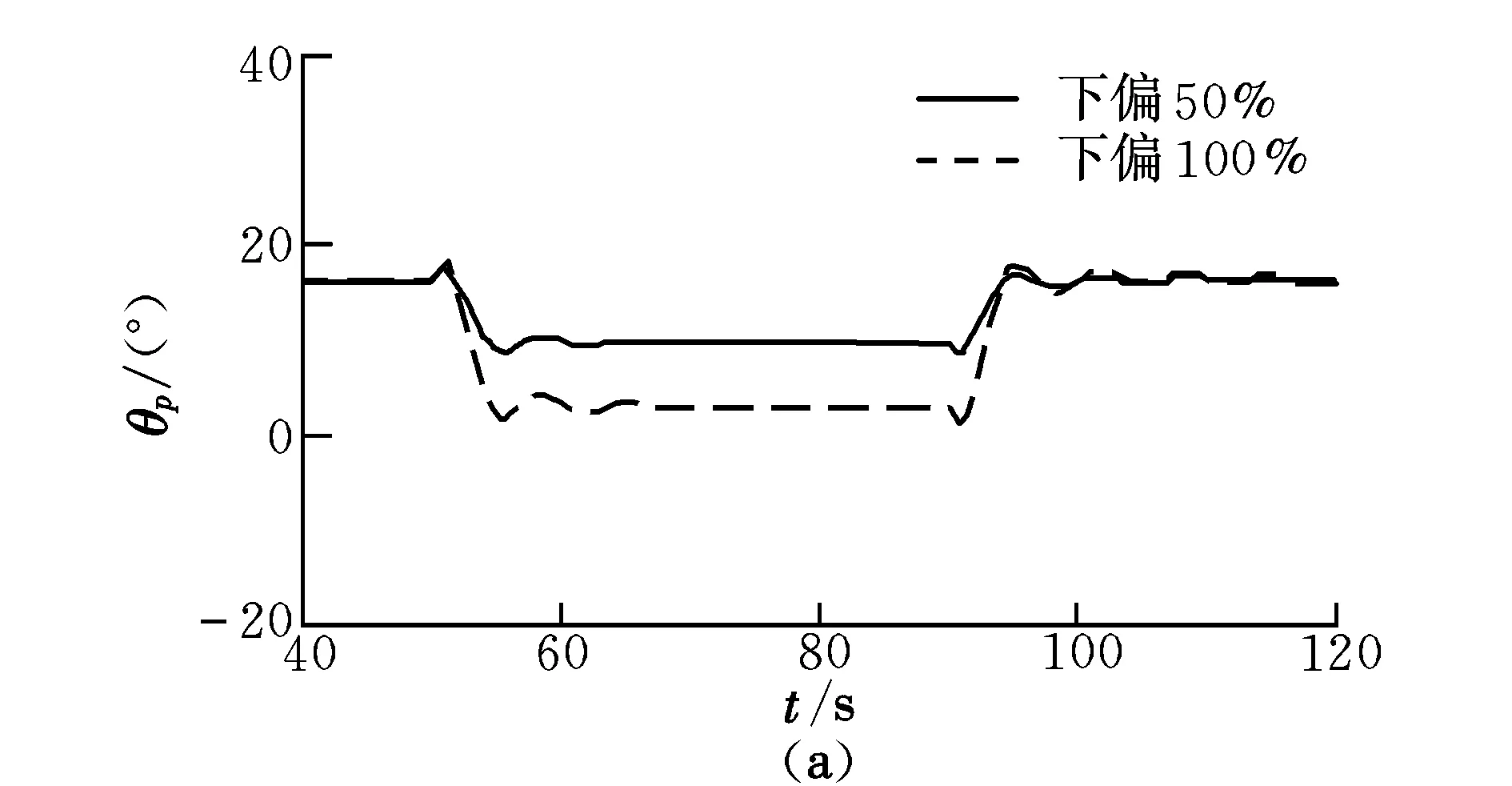
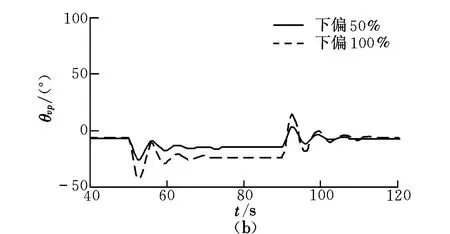
图6 翼伞俯仰角和相对俯仰角变化曲线Fig.6 Curves of pitch angle and relative pitch angle
由图6可知,雀降操纵时,俯仰角和相对俯仰角具有明显变化,且衰减速度较慢,说明存在明显的相对运动。当采取100%下偏操纵时,相对运动最严重,最大相对俯仰角为21°。
(4)侧风干扰响应
阵风采用NASA经典阵风模型。图7为翼伞姿态角变化曲线。由图7可以看出,遇侧风干扰时,翼伞俯仰角θp和滚转角φp变化幅度较小,此时翼伞向风力方向偏转,而负载存在一定滞后,进而产生最大幅值为10°~17°的瞬时偏航角ψp。扰动结束后,姿态角逐渐衰减恢复至初始状态,衰减时间较长。
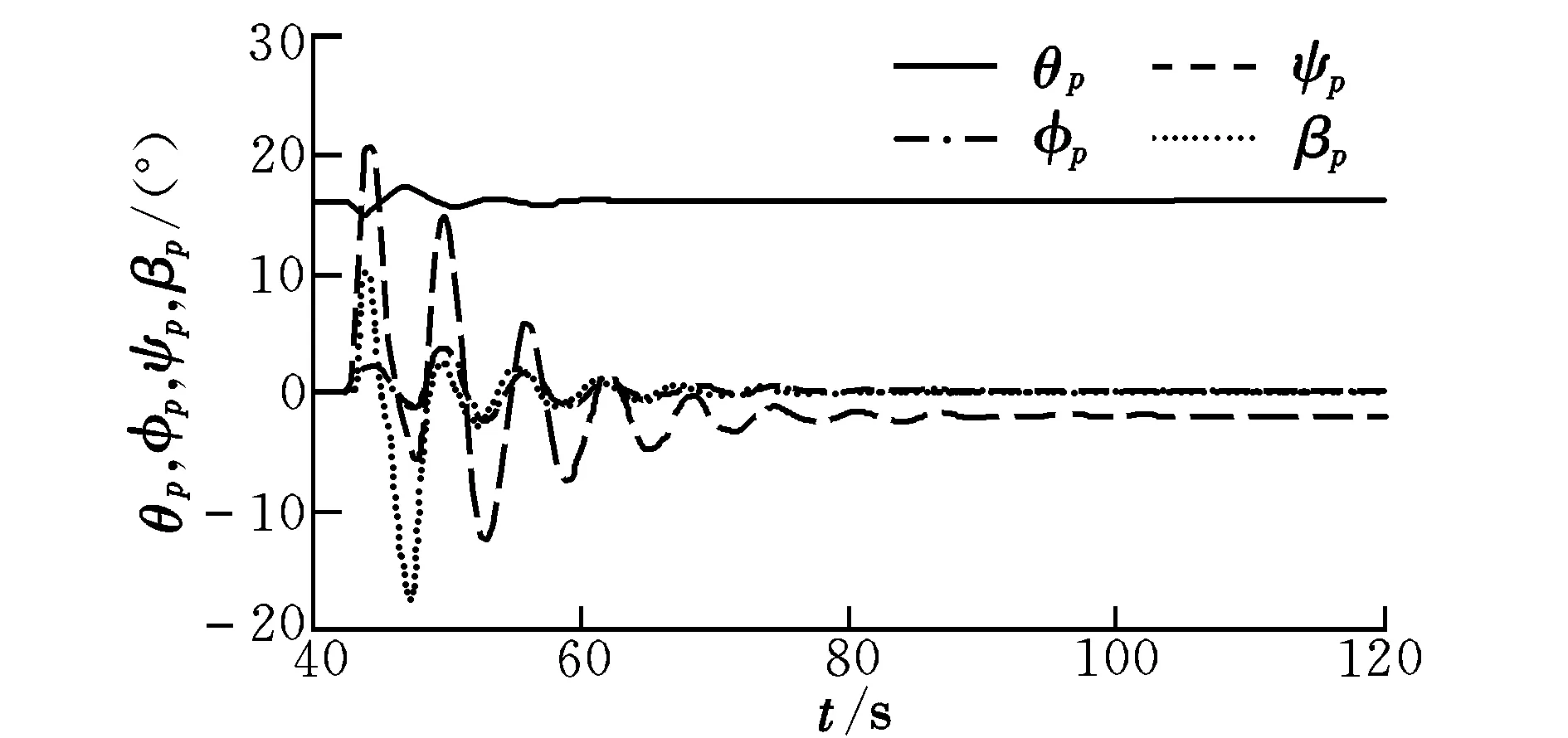
图7 姿态角变化曲线Fig.7 Change curves of the attitude angles
3 结束语
采用机理法建立了动力翼伞8-DOF非线性相对运动模型,分别仿真分析了动力翼伞稳定滑翔状态下对动力变化、转弯和雀降3种操纵以及遇变向阵风条件下的两体相对运动情况。研究结果表明,动力变化及雀降操纵时两体具有明显的相对俯仰运动,而转弯和遇侧风时具有相对偏航运动,同时证明所建模型可以用于解释和分析动力翼伞的相对运动问题。
但是值得注意的是:(1)该模型未考虑伞绳存在弹性形变时的相对运动情况;(2)仿真中控制量的施加采用阶跃形式,与实际操纵动作存在误差;(3)模型中尚未考虑实际控制响应过程存在的时延,这会对今后的控制策略研究产生影响。因此,针对以上问题,对模型的改进与实验验证以及抑制相对运动的控制策略设计将是今后的研究重点。
[1] Smith J,Bennett T,Fox R.Development of the parafoil landing system[R].AIAA-2009-1730,2009.
[2] Slegers N,Costello M.Model predictive control of a parafoil and payload system[J].Journal of Gaidance,Control,and Dynamics,2005,28(4):816-821.
[3] Slegers N.Effects of canopy-payload relative motion on control of autonomous parafoils[J].Journal of Gaidance,Control,and Dynamics,2010,33(1):116-125.
[4] Slegers N.Optimal control for terminal guidance of autonomous parafoils[R].AIAA-2009-2058,2009.
[5] Slegers N.Use of variable incidence angle for glide slope control of autonomous parafoils[J].Journal of Gaidance,Control,and Dynamics,2008,31(3):587-596.
[6] Chrystine M,Slegers N.Comparison and analysis of multi-body parafoil models with varying degrees of freedom [R].AIAA-2011-2615,2011.
[7] Ward M,Costello M.Parametric study of powered parafoil flight dynamics[R].AIAA-2012-4726,2012.
[8] Ward M.Flight test results for glide slope control of parafoil canopies of various aspect ratios[R].AIAA-2011-2620,2011.
[9] Ward M,Costello M.Specialized system identification for parafoil payload system[J].Journal of Gaidance,Control,and Dynamics,2012,35(2):588-597.
[10] Zaitsev P V,Formal’skii A M.Mathematical modeling of controlled longitudinal motion of a paraglider[J].Computational Mathematics and Modeling,2013,24(3):418-431.
[11] Song L,Yang H,Liu C.Study on powered-parafoil longitudinal flight performance with a fast estimation model[J].Journal of Aircraft,2013,50(5):1660-1667.
[12] Ochi Y.Modeling and simulation of nonlinear dynamics of a powered paraglider[R].AIAA-2008-7418,2008.
[13] Heise M,Muller S.Dynamic modeling and xisualization of multi-body flexible system[R].AIAA-2004-4809,
2004.
[14] Muller S,Wagner O,Sachs G.A high-fidelity nonolinear multibody simulation model for parafoil system[R].AIAA-2001-2120,2001.
[15] 熊菁.翼伞系统动力学与归航方案研究[D].长沙:国防科学技术大学,2006.
[16] Goodrick T F.Comparision of simulation and experimental data for a gliding parachut in dynamic[R].AIAA-1981-1924,1981.
[17] Barrows T.Apparent mass of parafoil with spanwise camber[J].Journal of Aircraft,2002,39(3):445-451.
(编辑:姚妙慧)
欢迎订阅2016年《飞行力学》杂志
《飞行力学》为航空航天飞行力学专业综合性学术刊物。本刊以反映当前飞机、直升机、导弹、航天器等飞行力学及相关专业的研究成果和报道国内外发展动态为宗旨;主要刊登飞行器的基础理论、制导与控制、试验与仿真、飞机综合设计、空中交通管制与导航、航空飞行技术等研究成果。
本刊主要面向从事航空、航天飞行力学专业的科研、教学、设计、试验、生产和使用等方面工作的专业技术人员、高等院校师生,以及陆、海、空军和民航部门的相关专业人员。对从事航空、航天相关学科研究的人员亦有所裨益。
本刊为双月刊,全年共出版6期,每册定价15元,全年90元。
发行部联系电话:029-86838448
飞行力学杂志社
2015年12月
Modeling and relative motion analysis of multi-body nonlinear dynamic of powered parafoil
CHEN Zi-li, ZHANG Hao, QIU Jin-gang
(Department of UAV Engineering, Ordnance Engineering College, Shijiazhuang 050003, China)
In the powered parafoil equipment for measurement and control are normally installed on payload, while the parafoil provids the main aerodynamic, so it is necessary to analyze the relative motion between two bodes. Considering the special structure of two-point flexible connection of powered parafoil and the added mass, an 8-DOF nonlinear dynamic model is proposed in this paper, in which the parafoil has 6-DOF and the payload has 2-DOF relative motion. Then, analysis of the relative motion is conducted in the control of horsepower change, turning, and flapping under stable gliding, or to lateral atmosphere disturbances. The results show the control of horsepower and flapping can result in the relative pitch motion between two bodies, while the relative yaw motion by the control of turning and disturbances, thus proving that the model is suitable for analyzing and explaining the phenomena and relative movement in powered parafil.
powered parafoil; two bodies; added mass; relative motion; lateral atmosphere
2015-03-11;
2015-06-16;
时间:2015-08-17 11:04
国家自然科学基金资助(51175508);总装院校创新工程基金资助(ZYX12080007)
陈自力(1964-),男,山西运城人,教授,博士生导师,研究方向为无人飞行器设计及无人系统导航、制导与控制。
V211.4
A
1002-0853(2015)06-0505-05
