飞翼布局折叠机翼变体飞机操稳特性研究

尹文强, 安然, 安玉娇

(中国飞行试验研究院 飞机所, 陕西 西安 710089)

飞翼布局折叠机翼变体飞机操稳特性研究

尹文强, 安然, 安玉娇

(中国飞行试验研究院 飞机所, 陕西 西安 710089)

为了研究飞翼布局折叠机翼变体飞机的操稳特性,自行设计飞翼布局折叠机翼变体飞机,建立研究模型并进行简化处理。采用涡格法和工程估算法对机翼折叠过程中飞机的纵向和横航向静稳定性进行分析;采用小扰动假设,将飞机扰动运动沿纵向和横航向解耦,分别得到纵向扰动运动和横航向扰动运动对应的模态,分析机翼折叠过程对飞机动稳定性的影响;结合工程估算法和CFD仿真分析机翼折叠过程对飞机操纵性的影响。飞行试验结果表明:在飞行中机翼折叠后,飞机有进入俯冲的趋势,随着配平舵偏角的增加,俯仰运动逐渐不够灵敏;在操纵杆量相同的情况下,机翼折叠状态的俯仰运动响应较快。

折叠机翼; 变体飞机; 操纵性; 稳定性

0 引言

目前,新概念飞行器设计理念层出不穷,飞行领域不断扩展,人类对飞行任务的综合要求不断提高,固定翼飞机越来越不能满足民用和军事方面的需求。从经济性和安全性考虑,人们要求新一代飞机能够在变化剧烈的飞行环境(高度、马赫数等)下和在执行多种任务(如起降、巡航、机动、盘旋、攻击等)时始终保持良好的性能[1]。

传统的变体飞机通过主动改变气动外形获得所需飞行性能[2]。这类飞机变形一般采用简单的机械传动装置来实现,虽然在某些方面满足了飞行要求,但大多是单自由度变形,在结构、重量、操纵性等方面付出的代价也较大。新型变体飞机是指采用智能材料和结构,通过流动控制和飞行控制技术,主动改变全机布局或气动外形,在不同飞行状态下均能获得最佳性能的飞行器[3]。本文所研究的折叠机翼变体技术是新型变体技术之一,飞机在飞行过程中通过机翼折叠改变机翼面积、展弦比等参数,以适应不同飞行状态的要求[4]。

1 模型简介

本文模型总体为飞翼布局,全机分为五段:中间段为机身;与机身连接处为内段机翼,前缘后掠为60°,后缘前掠为15°;内段机翼外侧为外段机翼,前缘后掠为40°,后缘后掠为15°。外段机翼可以向上折叠60°,同时内段机翼保持水平。模型采用S8025翼型,取机翼上反角为0°;为控制飞机的俯仰和滚转运动,在内段机翼上布置升降副翼,其偏转角度为-20°～30°;机翼后缘为W型;采用前三点式起落架系统;进气道位于机身背部。表1列出了模型的主要总体参数,其中:lw为翼载荷;θzd为机翼折叠角。由验证机总体参数绘制的CATIA模型如图1所示。

图1 验证机CATIA模型Fig.1 CATIA model of demonstration aircraft

在分析机翼折叠过程中的气动特性变化时,可以进行相应的简化处理[5],在实际计算中选取具有代表性的折叠角即可。本文在0°～60°范围内每隔10°建立一个模型进行计算,将得到的数据连成曲线,可以得到机翼折叠过程中全机气动特性的近似变化趋势[6]。

2 纵向稳定性分析

2.1 纵向静稳定性分析

飞机的纵向静稳定性可用偏导数CmCL及其正负来表示,其绝对值大小反映了飞机的纵向静稳定裕度,其计算公式为:

CmCL=(Cm-Cm0)/CL

(1)

计算时假定机翼折叠过程中全机的重心位置不变,经涡格法(Vortex Lattice Method, VLM)计算得出CmCL随不同机翼折叠角的变化曲线如图2所示。

图2 静稳定裕度随机翼折叠角的变化Fig.2 Change of CmCL with the wings folding angle

从图2可以看出,在机翼折叠过程中CmCL始终小于0,飞机具有纵向静稳定性。随着机翼折叠角的增大,焦点后移,在重心不变的情况下,静稳定裕度逐渐增大,机翼完全折叠时的静稳定裕度达到8.5%,对飞机纵向操纵性的影响在可接受范围内。由于采用S8025翼型,其零升俯仰力矩系数Cm0为正,飞机处于纵向静稳定时的迎角为正值。

2.2 纵向动稳定性分析

s4+A3s3+A2s2+A1s+A0=0

(2)

该特征方程有两对共轭复根,较大的共轭复根对应以迎角和俯仰角速度变化为特征的短周期运动,较小的共轭复根对应着以飞行速度和俯仰角变化为特征的长周期运动。

针对本文模型,计算出机翼展开和折叠状态下的长周期和短周期模态,并通过劳斯-霍尔维茨判据判断其纵向动稳定性[6]。

机翼展开状态,两对特征根分别为:

λ1,2=-9.225 6±5.136 7i

λ3,4=-0.144 1±0.677 8i

通过计算,可得机翼展开状态下短周期无阻尼振荡频率ωsp=10.559 2 rad/s,阻尼比ζsp=0.873 7,振荡周期Tsp=1.222 6 s,半衰期T1/2,sp=0.075 12 s;长周期无阻尼振荡频率ωp=0.693 rad/s,阻尼比ζp=0.207 88,振荡周期Tp=9.269 6 s,半衰期T1/2,p=4.810 7 s。

机翼完全折叠状态,两对特征根分别为:

λ1,2=-9.372 4±5.043 4i

λ3,4=-0.144 1±0.678i

通过计算可得,ωsp=10.643 2 rad/s,ζsp=0.880 6,Tsp=1.245 2 s,T1/2,sp=0.073 94 s;ωp=0.693 rad/s,ζp=0.207 9,Tp=9.27 s,T1/2,p=4.81 s。

由于机翼展开状态和折叠状态下特征根均具有负实部,故两种模态下验证机纵向运动都是稳定的。

3 纵向操纵性分析

对于本文研究模型,一般通过调节升降副翼对飞机的俯仰姿态进行操纵,两侧升降副翼同向偏转时作为升降舵使用。本节采用工程估算法结合CFD计算方法对本文模型的纵向操纵特性进行研究。

采用VLM方法[7]对飞机在机翼折叠过程中的全机俯仰力矩系数Cm进行估算。设定升降副翼偏转30°,故俯仰力矩系数对副翼偏角的导数为:

Cmδea=ΔCm/30

(3)

采用CFD方法对验证机不同折叠角状态的气动特性进行计算，将其作为对工程估算法的补充。在划分网格时,对飞机曲面进行简化处理,将发动机进气道和尾喷口进行封闭作为机体表面。

在2°迎角下建立升降副翼偏转和不偏转时不同机翼折叠角的网格模型,通过计算得到不同机翼折叠角下升降副翼操纵导数。采用工程估算法和CFD方法计算得到的结果如图3所示。

图3 Cmδea随机翼折叠角的变化Fig.3 Change of Cmδea with the wings folding angle

由图3可知,升降副翼操纵导数绝对值随机翼折叠角的增加稍有增加,CFD计算值和VLM工程估算值变化趋势相同。本文模型外段机翼折叠面积相对于整个机翼面积比例较小,机翼从展开到折叠的过程中,全机机翼参考面积稍微减小,平均气动弦长变化较小。由于升降副翼偏转所需力矩大小保持不变,由力矩计算公式可知,升降副翼操纵导数随机翼折叠角的变化符合图4变化趋势。

定直平飞飞机的俯仰力矩系数为零,在特定迎角和特定折叠角下的副翼偏角计算公式为:

δea=-(Cm0+Cmαα)/Cmδea

(4)

得到飞机定直平飞所需舵偏角随机翼折叠角的变化曲线如图4所示。

图4 δea随机翼折叠角变化曲线Fig.4 Change of δea with the wings folding angle

从图4可以看出,对于飞机的配平舵偏角,CFD计算值和VLM工程估算值变化趋势相差较大,随着机翼折叠角的增加,操纵导数绝对值增加。理论上纵向操纵应更加灵敏,但随着折叠角的增加，力矩系数绝对值也增加,对飞机操纵性的影响甚至超过了操纵导数,最终导致平飞时配平舵偏角持续增大。通过比较可知，CFD计算的变化趋势更具可信度。

由图4可知，升降副翼操纵导数较小,说明升降副翼操纵作用偏弱。在设计时可增加一组重心调整机构[6],飞行中通过调整飞机重心来减小飞行过程中机翼折叠后的力矩系数,使配平舵偏角不至于过大。

4 横航向稳定性分析

4.1 横航向静稳定性分析

飞机的横向静稳定性采用滚转力矩系数Cl对侧滑角β的导数Clβ表示,飞机横向静稳定的标志是Clβ<0。Clβ随机翼折叠角的变化曲线如图5所示。可以看出,机翼从展开到折叠过程中Clβ始终为负,飞机满足横向静稳定性要求。

图5 Clβ随机翼折叠角的变化Fig.5 Change of Clβ with the wings folding angle

飞机的航向静稳定性采用偏航力矩系数Cn对侧滑角β的导数Cnβ表示,飞机航向静稳定的标志是Cnβ<0。Cnβ随机翼折叠角的变化曲线如图6所示。由图6可以看出，机翼从展开到折叠过程中,Cnβ由0.000 37单调增加到0.000 93,说明飞机始终具有航向静稳定性。

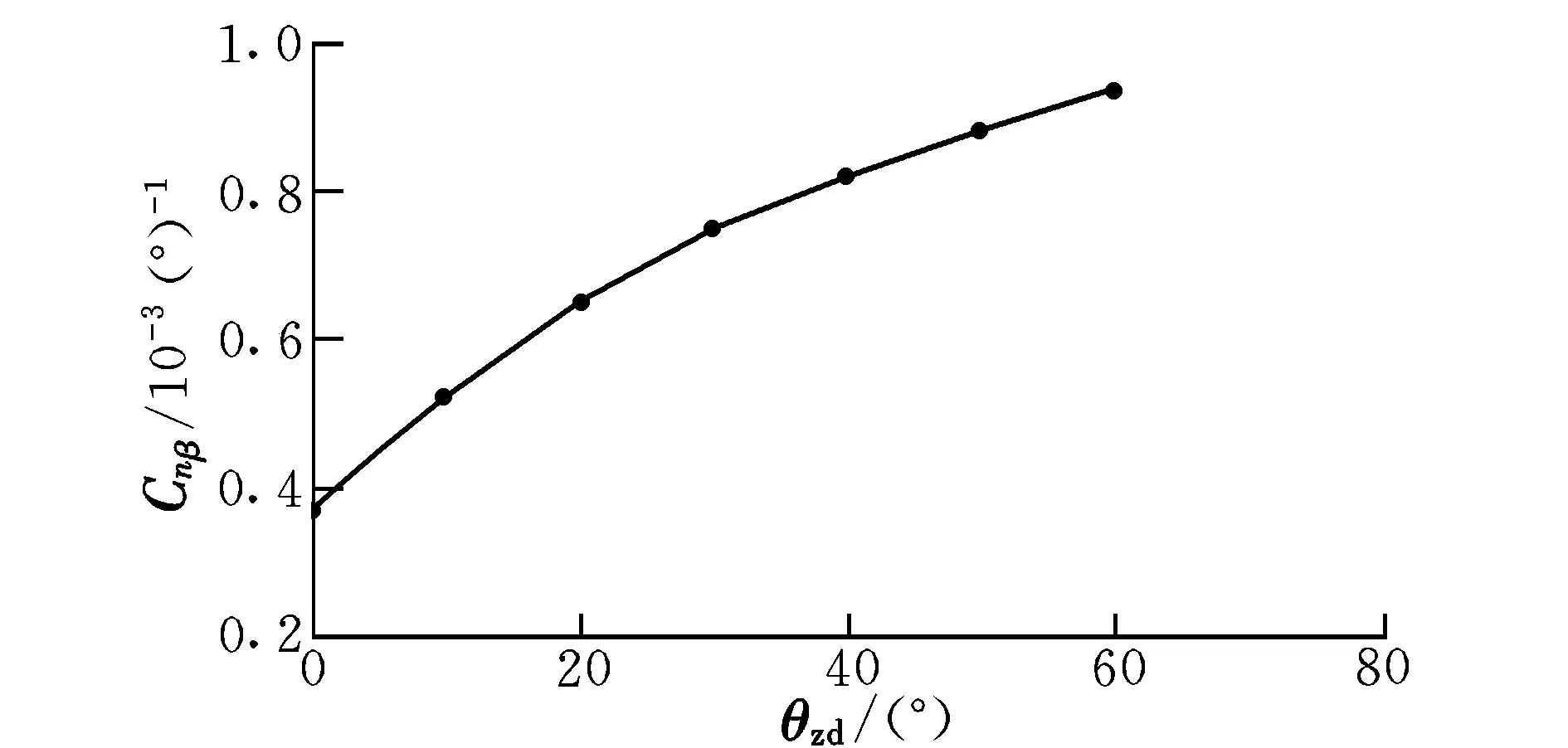
图6 Cnβ随机翼折叠角的变化Fig.6 Change of Cnβ with the wings folding angle

4.2 横航向动稳定性分析

采用飞机横航向小扰动方程组得到特征方程:

s4+A3s3+A2s2+A1s+A0=0

(5)

该特征方程有1个大的负实根,1个小的正实根和一对共轭复根,故特征方程可写为:

(s-λr)(s-λs)(s2+2ζdωds+ωd2)=0

(6)

其中较大的负实根λr对应滚转模态,较小的正实根λs对应螺旋模态,一对共轭复根对应荷兰滚模态。

(1) 滚转模态

结合本文模型计算,机翼展开时λr=-10.931,时间常数Tr=0.091 5 s;当机翼折叠时,λr=-10.186,Tr=0.098 2 s。由于特征根为大的负实根,因此飞机在扰动初期做迅速衰减的滚转阻尼运动。机翼展开和折叠状态的半衰期T1/2,p分别为0.063 4 s和0.068 04 s。对比以上数据,机翼折叠状态具有更好的滚转模态稳定性。由于机翼展开和折叠状态的负实根数值相差不大,因此机翼折叠对滚转模态特性影响较小。

(2) 螺旋模态

螺旋模态稳定的判定依据为:

LβNr-NβLr>0

(7)

结合本文模型,带入数据计算可以得到飞机在展开和折叠状态下LβNr-NβLr的值均小于0,飞机的螺旋模态是不稳定的。

本文模型机翼展开状态下螺旋模态的特征根为λs=0.126 3,倍幅时间T2s=3.499 s;机翼折叠状态下λs=0.484,T2s=1.918 9 s。对比上述数据可以看出,机翼展开和折叠状态的特征根相差较大,机翼折叠对螺旋模态特性影响较大。飞行控制设计时须采取一定的增稳控制来改善螺旋模态。

(3) 荷兰滚模态

结合本文模型,带入数据计算可以得到机翼展开状态下无阻尼振荡频率ωd=2.025 8 rad/s,阻尼比ζd=0.349 6,振荡周期Td=3.304 4 s,半衰期T1/2,d=0.978 5 s,荷兰滚模态的特征根λd=-0.7082±1.898i;机翼折叠状态下ωd=3.35 rad/s,ζd=0.31,Td=1.67 s,T1/2,d=0.68 s,λd=-1.025±3.186i。由分析可知,机翼折叠过程中飞机荷兰滚模态始终是稳定收敛的。

5 横航向操纵性分析

对于本文模型,控制飞机横航向操纵性能的部件为升降副翼。升降副翼差动偏转引起的滚转力矩系数导数又称副翼操纵效率Clδea,计算得到Clδea随机翼折叠角的变化曲线如图7所示。

图7 Clδea随机翼折叠角的变化Fig.7 Change of Clδea with the wings folding angle

由图7可以看出,随着机翼折叠角的增加,副翼操纵效率除了在30°左右振荡之外,绝对值逐渐增大。因此,机翼折叠后副翼操纵效率较高,滚转操纵更加灵活。

升降副翼差动偏转引起的偏航力矩系数导数也称副翼偏航操纵导数Cnδea,计算得到Cnδea随机翼折叠角的变化曲线如图8所示。

图8 Cnδea随机翼折叠角的变化Fig.8 Change of Cnδea with the wings folding angle

由图8可以看出,随机翼折叠角的增加,副翼偏航操纵导数数值波动较大。总体上机翼展开状态和折叠状态的副翼航向操纵导数绝对值增大,提高了操纵效率。

6 试飞验证

为了验证该飞机的操稳特性计算结果,依据总体参数制作验证机模型进行试飞验证。验证机机翼可以完全按照设计要求进行折叠和展开,试飞验证机模型如图9所示。

图9 验证机模型Fig.9 Demonstration aircraft model

在飞行中机翼折叠后,飞机有进入俯冲的趋势。为保证平飞,操纵手增加了升降副翼配平舵偏角。飞行中舵偏角变化量与计算值较为吻合,随着舵偏角的增加,俯仰运动逐渐不够灵敏。为了验证飞机的操纵特性,操纵手在机翼展开和完全折叠状态下各做了一次推杆和拉杆操纵,在操纵杆量相同的情况下,机翼折叠状态的俯仰运动响应较快,这与前文分析结果一致。

7 结束语

本文通过研究自行设计的变体飞机的操稳特性,分析机翼折叠对飞机纵向和横航向操稳特性的影响,发现验证机设计时需要注意的问题并提出相应的措施,例如升降副翼操纵作用偏弱和验证机螺旋模态不稳定等。较大机翼折叠角时的翼身干扰问题以及机翼折叠部位的缝隙整流等问题,需要在验证机设计时,从总体设计、飞行控制、先进材料以及机电一体化等方面来解决。在后期工作中,需要对飞机飞行状态改变时机翼折叠角变化的动态响应作进一步的分析,从而达到全面掌握折叠机翼变体飞机运动规律的目的。

[1] 陆宇平,何真,吕毅.变体飞行器技术[J].航空制造技术,2008(22):26-29.

[2] 李军府,艾俊强,董海锋.飞机变形技术发展探究[J].航空科学技术,2009(2):3-5.

[3] 李闻,宋笔锋,张炜.飞翼布局无人机变形机翼设计与模型验证研究[J].飞行力学,2010,28(4):17-20.

[4] 廖波,袁昌盛,李永泽.折叠机翼无人机的发展现状和关键技术研究[J].机械设计,2012,29(4):1-5.

[5] Yue T,Wang L,Ai J.Multibody dynamic modeling and simulation of a tailless folding wing morphing aircraft[R].AIAA-2009-6155,2009.

[6] 金鼎,张炜,艾俊强.折叠机翼变体飞机纵向操纵性与稳定性研究[J].飞行力学,2011,29(1):5-8.

[7] Margason R J,Lamar J E.Vortex-lattice FORTRAN program for estimating subsonic aerodynamic characteristics of complex planforms[M].Washington D C:NASA Technical Note D-6142,1971:10-32.

(编辑：李怡)

Study on controllability and stability of flying wing and folding wing morphing aircraft

YIN Wen-qiang, AN Ran, AN Yu-jiao

(Aircraft Flight Test Technology Institute, CFTE, Xi’an 710089, China)

To study the controllability and stability of flying wing and folding wing morphing aircraft, the aircraft was self-designed; the model was established and simplified. The longitudinal and lateral-directional static stability during the wings folding process of the aircraft were analyzed with vortex lattice method and the engineering estimation method. Using the small perturbation hypothesis, the aircraft perturbation motion were decoupled along the longitudinal and lateral-directional, and the corresponding modality of longitudinal perturbation motion and transverse heading perturbation motion were obtained. The effects on the dynamic stability of the aircraft during the wings folding process were analyzed. Combining the engineering estimation method and CFD simulation method, the effect on the controllability of the aircraft during the wings folding process were analyzed. Flight test results indicate that the aircraft tend to the dive motion when the wings folded, and the sensitivity of the pitching motion declines gradually with the increase of the trim rudder deflection. Under the condition of same joystick offset, the pitching motion with wings folding state has a faster response speed.

folding wing; morphing aircraft; controllability; stability

2015-02-03;

2015-04-17;

时间:2015-06-24 15:03

尹文强(1989-)，男，河南驻马店人，助理工程师，硕士，研究方向为无人机试飞研究。

V212.12

A

1002-0853(2015)06-0495-05