基于多体动力学的大型翼伞系统飞行仿真分析

陈建平, 宁雷鸣, 张红英, 童明波

(南京航空航天大学 航空宇航学院, 江苏 南京 210016)

基于多体动力学的大型翼伞系统飞行仿真分析

陈建平, 宁雷鸣, 张红英, 童明波

(南京航空航天大学 航空宇航学院, 江苏 南京 210016)

飞行动力学分析是大型翼伞系统设计及归航方案研究的重要基础。为此,提出了基于多体系统动力学理论的大型翼伞系统飞行动力学仿真分析方法,给出了相应的多体系统模型,建立了系统的运动学约束方程组和飞行动力学变分方程组。通过引入拉格朗日乘子,获得了大型翼伞系统封闭的飞行动力学方程组,对某大型翼伞系统的飞行动力学过程进行了仿真计算。结果表明,与小型翼伞系统相比,大型翼伞系统的稳定滑翔速度大、抗外界干扰能力强、转弯半径大、转弯周期长、操纵响应慢。此外,风速和风向对大型翼伞系统的飞行轨迹和着陆点的位置有明显影响。对于同一具翼伞,回收物重量和初始高度是影响留空时间的主要因素。所提方法可以有效、准确地应用于大型翼伞系统的飞行动力学仿真分析。

翼伞系统; 飞行动力学; 多体系统; 动力学建模; 数值仿真

0 引言

翼伞系统具有良好的滑翔性能、操纵性能和定点雀降着陆性能,被广泛应用于民用和军事领域[1-2]。为此,国内外许多学者对其进行了深入的研究。Nicolaides[3]、朱旭等[4]通过实验和数值模拟的方法,分析了翼伞的气动特性;Timothy[5]详细讨论了翼伞附加质量和附加质量惯性矩的计算;文献[6-9]建立了翼伞系统不同自由度的力学模型,研究了翼伞的飞行性能;文献[10-12]对翼伞系统的航迹规划和跟踪控制问题进行了深入研究;文献[13-15]建立了动力翼伞的动力学模型,分析了有关参数对动力翼伞飞行性能的影响。大型翼伞系统在重装精确空投和大型飞行器定点回收方面具有广泛的应用前景。2001年,美国X-38无人飞行器飞行试验使用的翼伞系统,其翼伞面积达700 m2左右,且投放海拔高度高[1]。这次成功的试飞验证了大型翼伞技术在大型航天器定点回收方面应用的可行性,但目前国内外对于大型翼伞系统飞行动力学的研究尚不多见。

与小型翼伞系统相比,大型翼伞系统具有回收物重量大、飞行速度快、翼载荷大等特点,因此系统的抗风能力变强,操纵性能变差,容易产生动力失速。本文针对大型翼伞系统的这些特点,应用多体系统动力学理论,建立了大型翼伞系统的运动学约束方程和飞行动力学方程。通过仿真计算,分析了大型翼伞系统的滑翔性能、转弯性能及风对上述性能的影响,这项研究对大型翼伞的系统设计及归航方案研究具有重要的应用价值。

1 大型翼伞系统运动学描述

如图1所示，大型翼伞系统由翼伞和回收物组成，翼伞和回收物通过伞绳汇交点C相连。假设翼伞展向对称，充满后具有固定的形状(后缘操纵除外)，同时为了充分考虑翼伞和回收物间存在的三个空间转动自由度,将汇交点C视为球铰约束。仿真分析中视地球为平面大地。

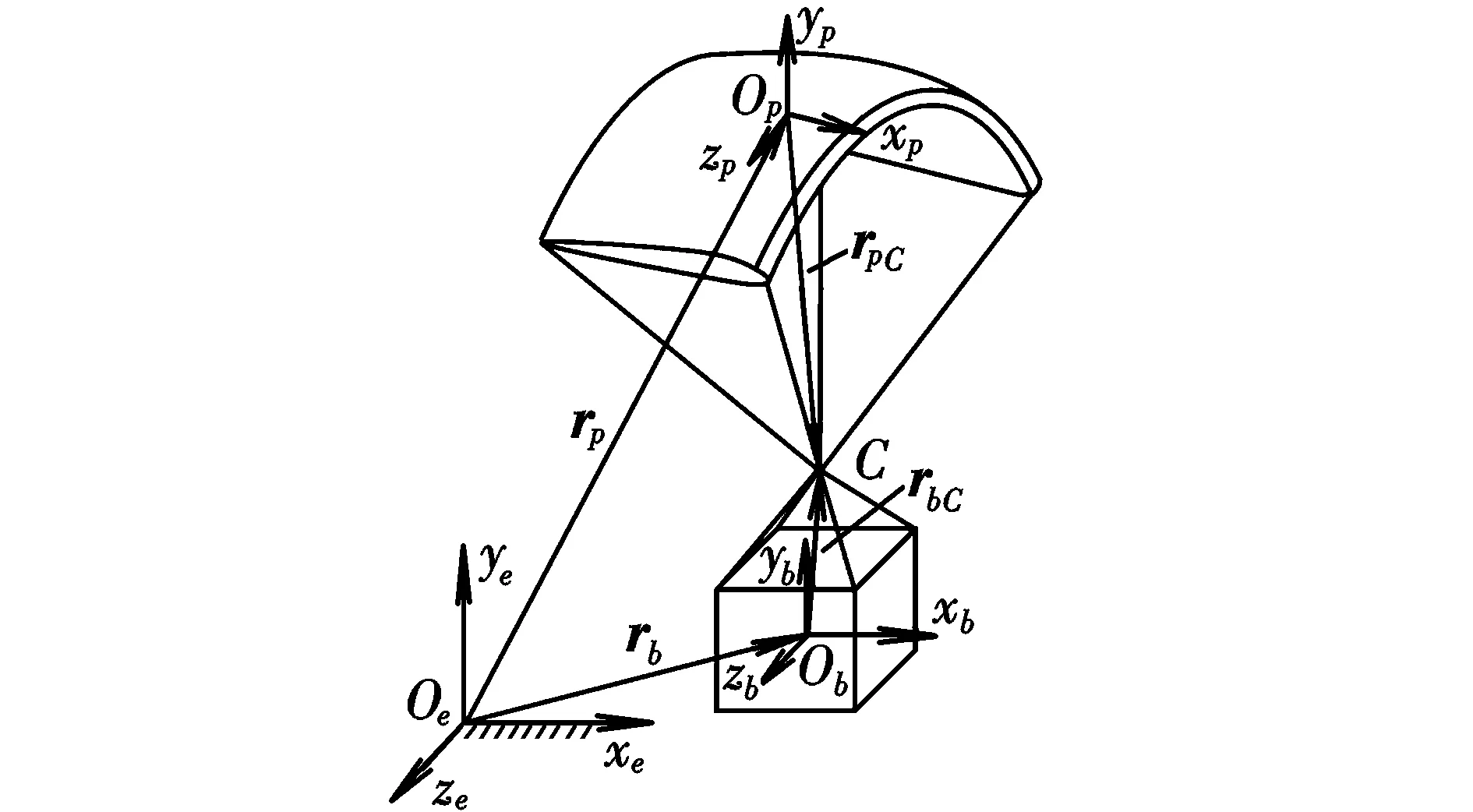
图1 大型翼伞系统Fig.1 A large parafoil-payload system

定义坐标系如下:大地坐标系Oexeyeze、翼伞连体坐标系Opxpypzp和回收物连体坐标系Obxbybzb,其中翼伞和回收物的质心Op和Ob相对Oe的位置为rp=(xp,yp,zp)T和rb=(xb,yb,zb)T;Opxpypzp相对Oexeyeze的姿态用偏航角ψp、俯仰角θp和倾斜角γp表示,Θp=(ψp,θp,γp)T;Obxbybzb相对Oexeyeze的姿态用偏航角ψb、俯仰角θb和倾斜角γb表示,Θb=(ψb,θb,γb)T。则翼伞的角速度和姿态坐标之间的关系为[16]:

(1)

类似地,回收物的角速度和姿态坐标之间的关系为:

(2)

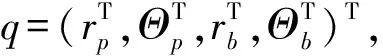
rp+AeprpC-(rb+AebrbC)=0

(3)

将上式简写为:

Φ(q)=0

(4)

式中:Aep和Aeb分别为Opxpypzp和Obxbybzb关于Oexeyeze的方向余弦矩阵;rpC为点C相对Op的位置矢量在Opxpypzp中的坐标阵;rbC为点C相对Ob的位置矢量在Obxbybzb中的坐标阵。

将式(4)对时间求导,可得整个大型翼伞系统的速度约束方程和加速度约束方程分别为:

(5)

(6)

2 大型翼伞系统飞行动力学描述

2.1 附加质量和附加质量惯性矩

由于翼伞自身的质量与其特征面积之比很小,因此分析翼伞系统的动力学特性时必须考虑附加质量的影响[2]。为了简便起见,不考虑翼伞展向弧形对附加质量和附加质量惯性矩的影响,翼伞的附加质量Mpa和附加质量惯性矩Jpa参见文献[5]。

2.2 气动力和气动力矩

为了描述翼伞受到的气动力和气动力矩,定义翼伞的气流坐标系Opxqyqzq,如图2所示。图中,vp为空速;αp为迎角;βp为侧滑角。

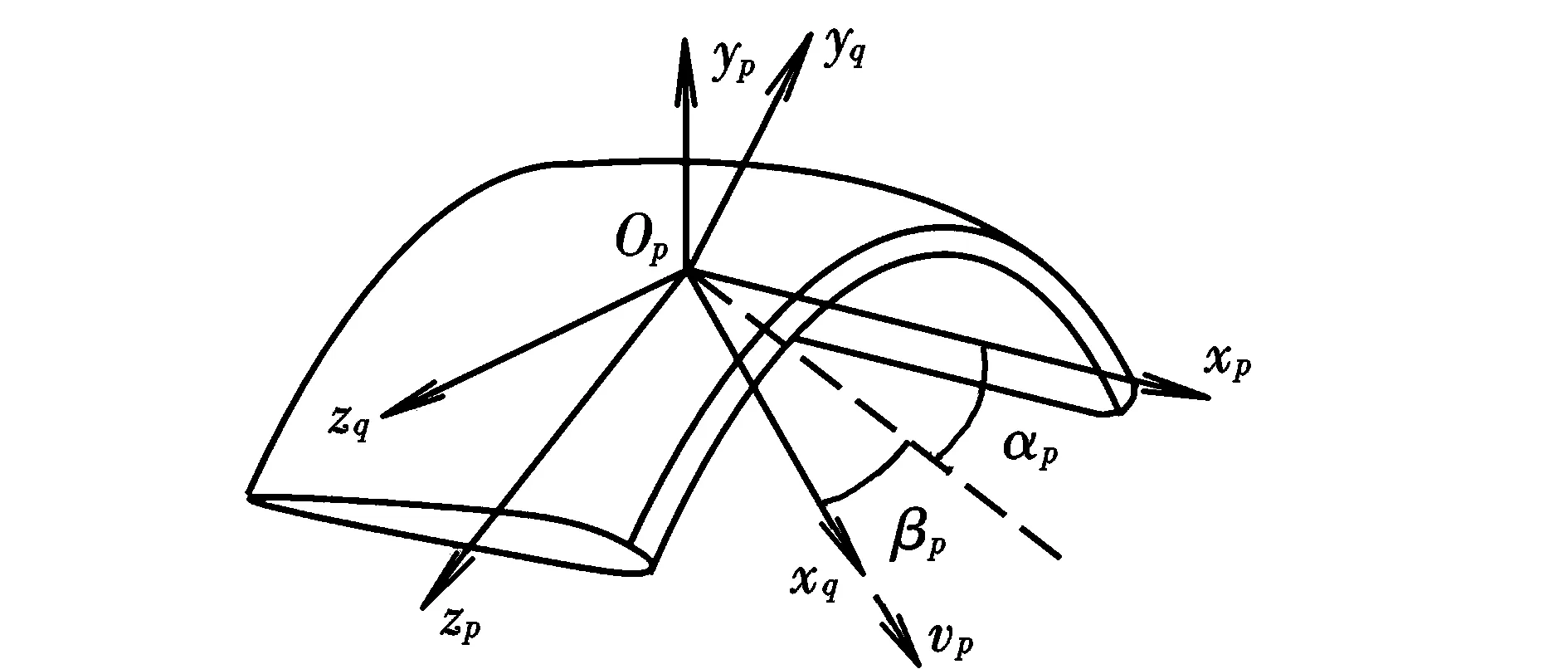
图2 坐标系Opxqyqzq和OpxpypzpFig.2 Reference frame Opxqyqzq and Opxpypzp

翼伞在飞行过程中受到的气动力和力矩为:

(7)

(8)

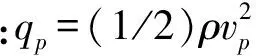
定义回收物的气流坐标系Obxryrzr如图3所示。图中,vb为回收物的空速;αb为回收物的迎角;βb为回收物的侧滑角。

图3 坐标系Obxryrzr和ObxbybzbFig.3 Reference frame Obxryrzr and Obxbybzb

回收物只考虑气动阻力,则其在飞行过程中受到的气动力为:

(9)

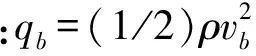
2.3 空气密度模型和风速模型

为了考虑空气密度随高度的变化,采用的空气密度模型为[17]:

ρ=ρ0(1-2.255 77×10-5H)4.255 88

(10)

式中:ρ0=1.225 kg/m3为海平面上的空气密度;H为翼伞的海拔高度(≤11 000 m)。此外,还考虑了风对大型翼伞系统飞行的影响,风速随高度的变化如下:

v=v0(H/H0)0.2

(11)

式中:v0为高度H0的风速,文中取H0=30 m。

2.4 大型翼伞系统飞行动力学方程

应用多体系统动力学理论[16],大型翼伞系统的飞行动力学变分方程为:

(12)

式中:M和Q分别为大型翼伞系统的广义质量阵和广义主动力阵,其表达式为:

M=HTZH

(13)

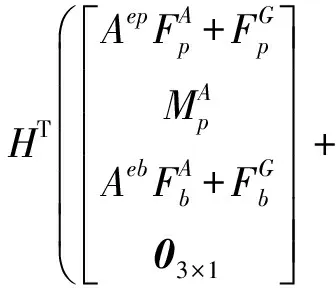
(14)

H=diag(IDpIDb)

(15)

Z=diag(mpI+AepMpaAepTJp+JpambIJb)

(16)

(17)

(18)

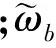
考虑加速度约束方程式(6),则大型翼伞系统封闭的飞行动力学方程为:

(19)

式中:λ为拉格朗日乘子,与翼伞和回收物在点C的约束力有关。

3 仿真结果及分析

应用上述方法,首先对文献[7]中翼伞系统的制动操纵过程进行了数值仿真,所得结果如图4所示。通过比较可见,仿真结果与文献[7]的结果一致,从而验证了本文方法的正确性。

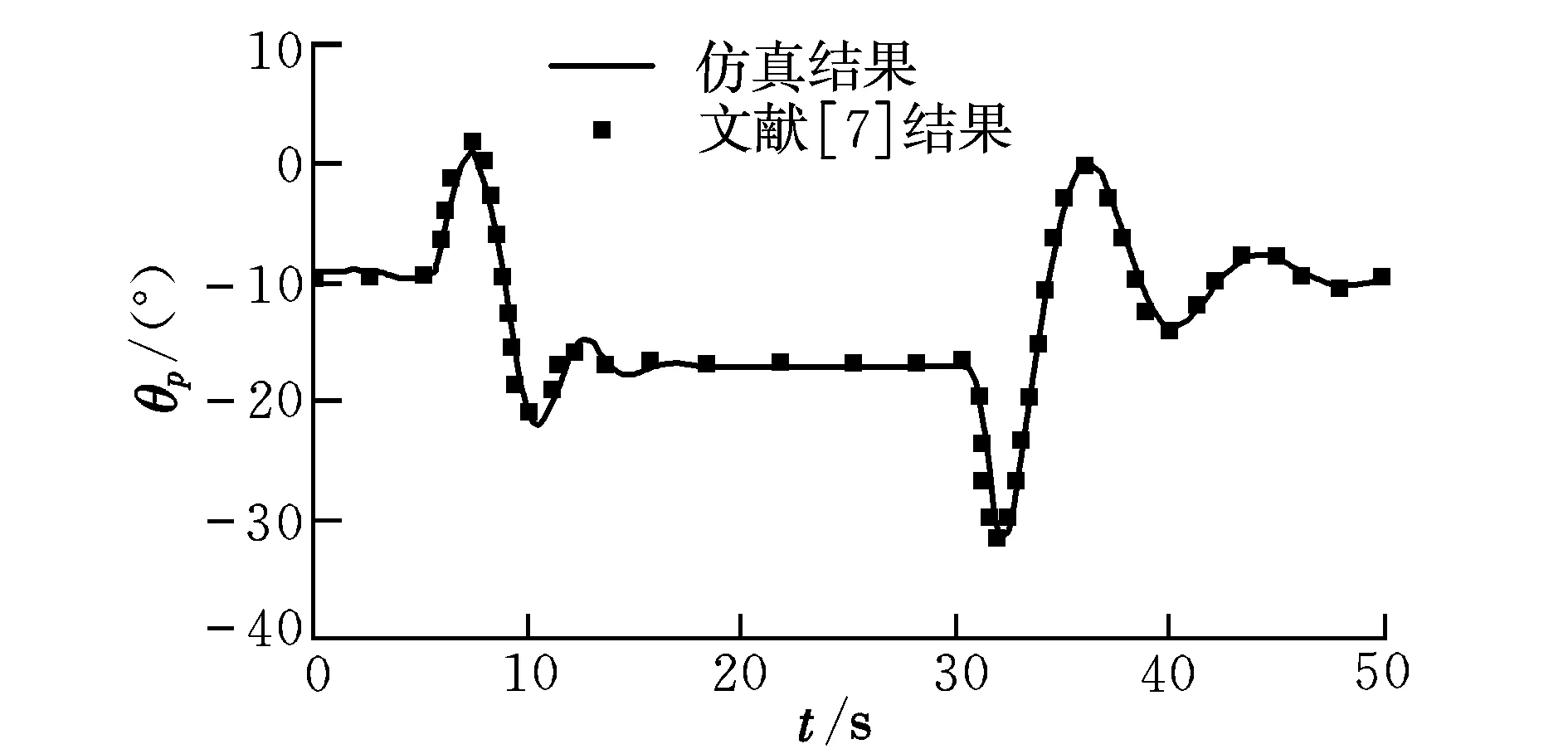
图4 仿真结果与文献[7]结果的比较Fig.4 Comparison of the results of simulation and in reference [7]

以下针对某大型翼伞系统进行飞行仿真分析,其主要几何参数和质量参数为:弦长14 m,展长39.3 m,翼型厚度2.1 m,安装角6°,翼伞质量300 kg,翼伞特征面积550 m2,回收物质量16 000 kg,回收物特征面积95.34 m2。翼伞的升力系数CpL、阻力系数CpD和俯仰力矩系数Cpmz如图5所示。翼伞系统的初始条件如下:x=z=0 m,y=5 000 m,vpx=34.320 m/s,vpy=-6.864 m/s,vpz=0 m/s,ψp=θp=γp=0°,ωpy=ωpz=ωpx=0 (°)/s。

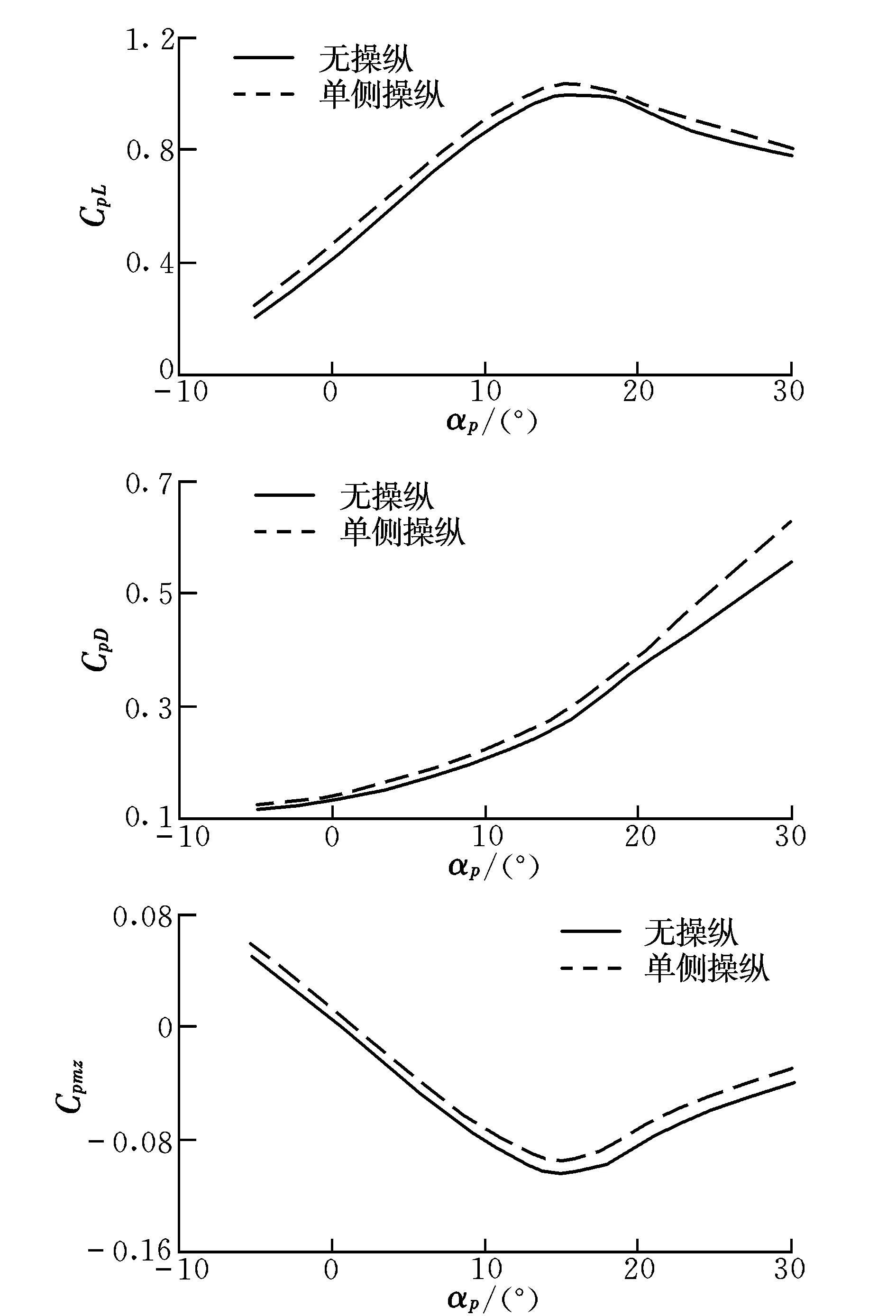
图5 翼伞的气动力系数Fig.5 Aerodynamic coefficients of the parafoil

为了进行比较,分别计算了无任何操纵、单侧操纵无风及单侧操纵有风情况下翼伞系统的飞行动力学响应。

(1)无任何操纵。假设翼伞系统在3 000～2 000 m高度遭遇沿-x方向、峰值为15 m/s的突风,突风风速变化如下:

v=

(20)

式中:y为翼伞系统的飞行高度。

仿真结果如图6所示。由图可知,没有突风时,翼伞系统大约经过50 s后作稳定滑翔飞行,此时θp为-3.1°,滑翔比为3.05。遭遇-x向突风时,θp剧烈振荡。虽然风速峰值很大,但离开突风区后翼伞系统仍能恢复到稳定滑翔状态,说明大型翼伞系统的抗干扰能力较强,这主要是由于大型翼伞系统的惯性及气动阻尼较大所致。

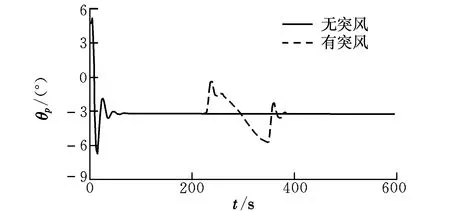
图6 无操纵时θp的时间历程Fig.6 Time histories of θp with no control

(2)单侧操纵无风。仿真结果如图7和图8所示。由图可知,翼伞的飞行轨迹为螺旋线,转弯半径约为660 m,水平面内的速度和铅垂速度均随时间的增加有所减小。

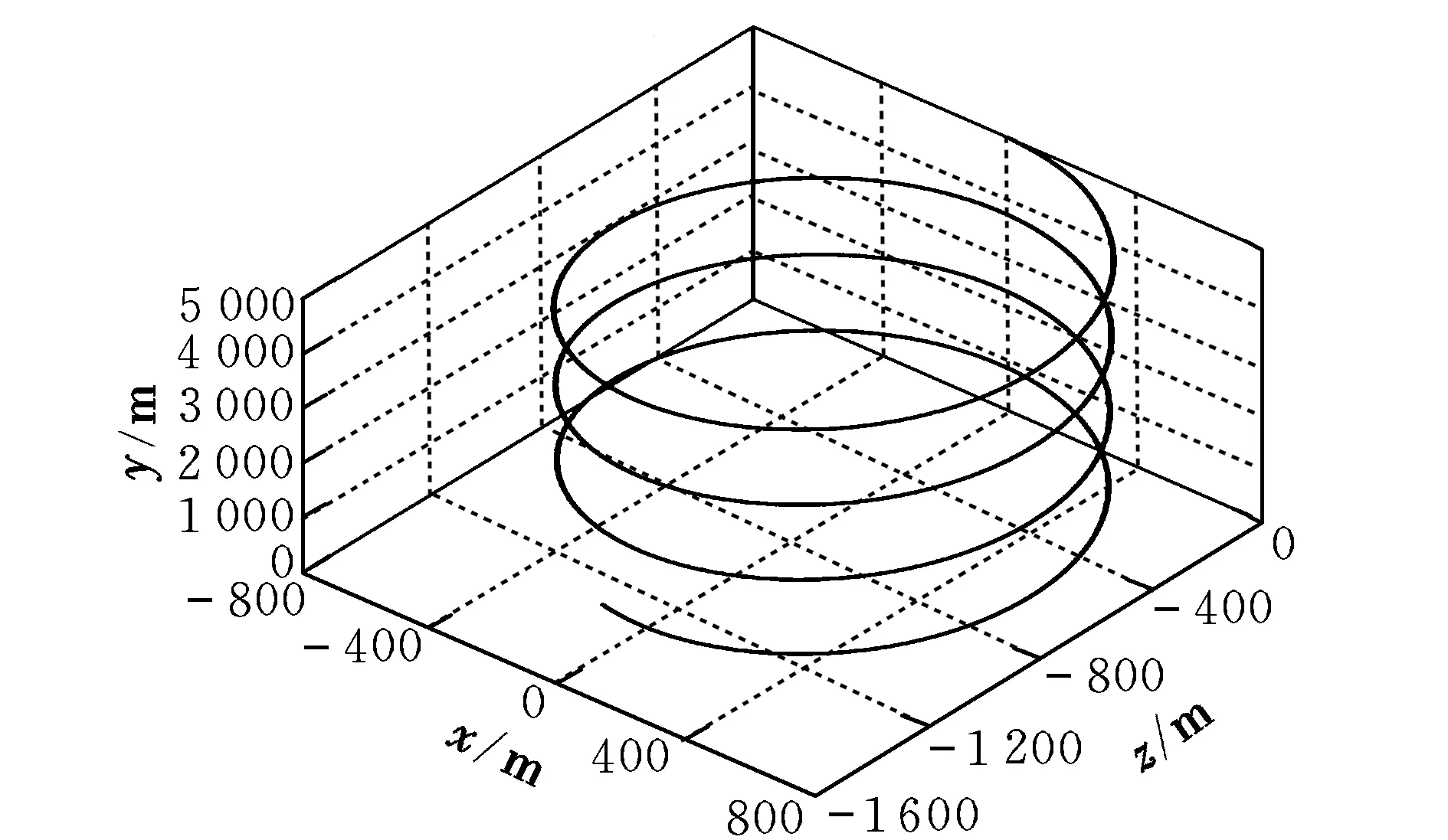
图7 单侧操纵无风时翼伞的飞行轨迹Fig.7 Flight trajectory of the parafoil with one-side control and without the influence of wind

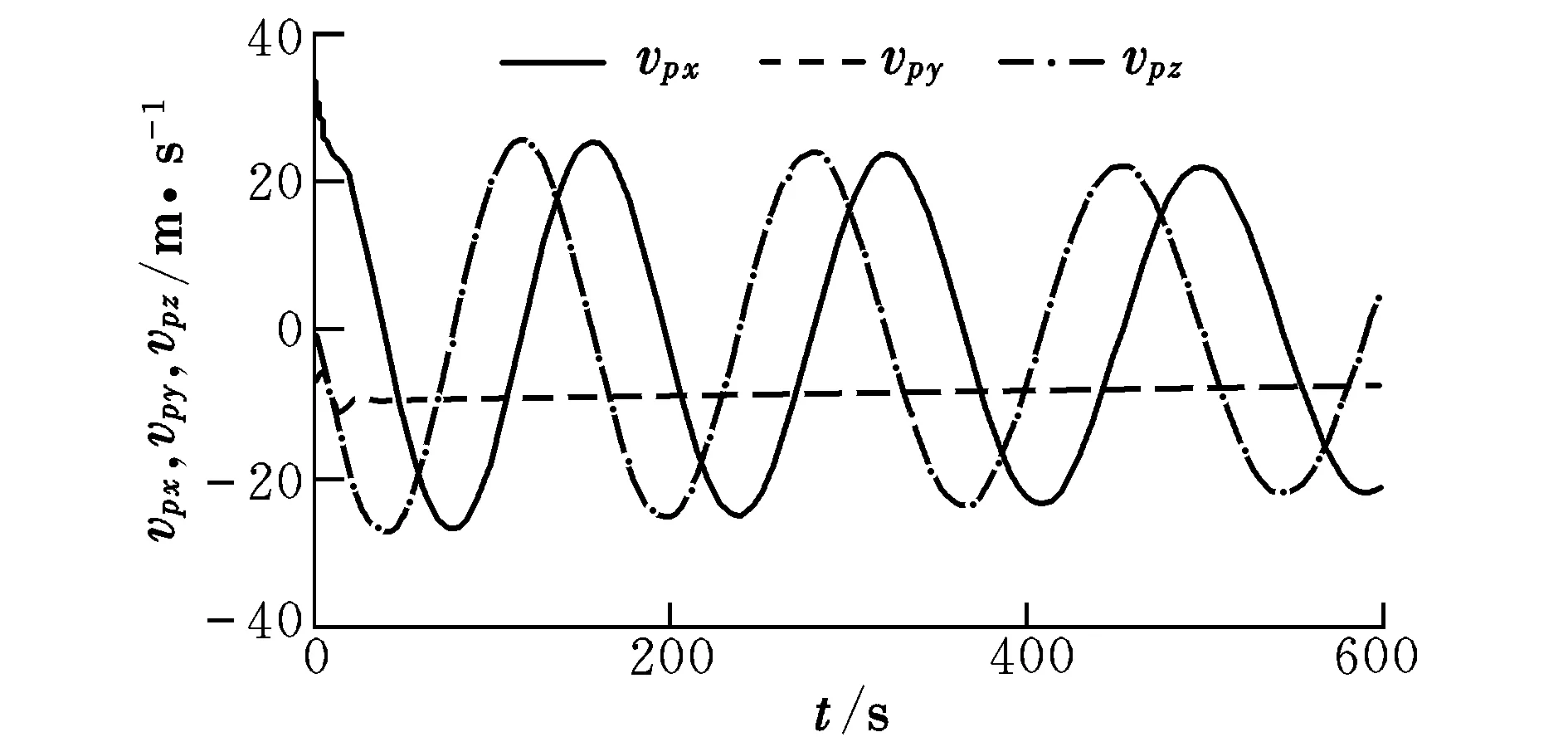
图8 单侧操纵无风时翼伞速度的时间历程Fig.8 Time histories of velocity of the parafoil with one-side control and without the influence of wind

(3)单侧操纵有风。假设30 m高度水平风速为4 m/s,沿-z方向,风速模型由式(11)确定。仿真结果如图9和图10所示。将图9与图7、图10与图8进行比较可知,翼伞的飞行轨迹顺着风向偏离,偏离距离接近风速关于时间的积分,同时翼伞在风向方向的速度也有明显改变,但铅垂速度变化甚微,因此翼伞系统的留空时间基本保持不变。此外,操纵量不变时,翼伞的转弯半径也基本保持不变。

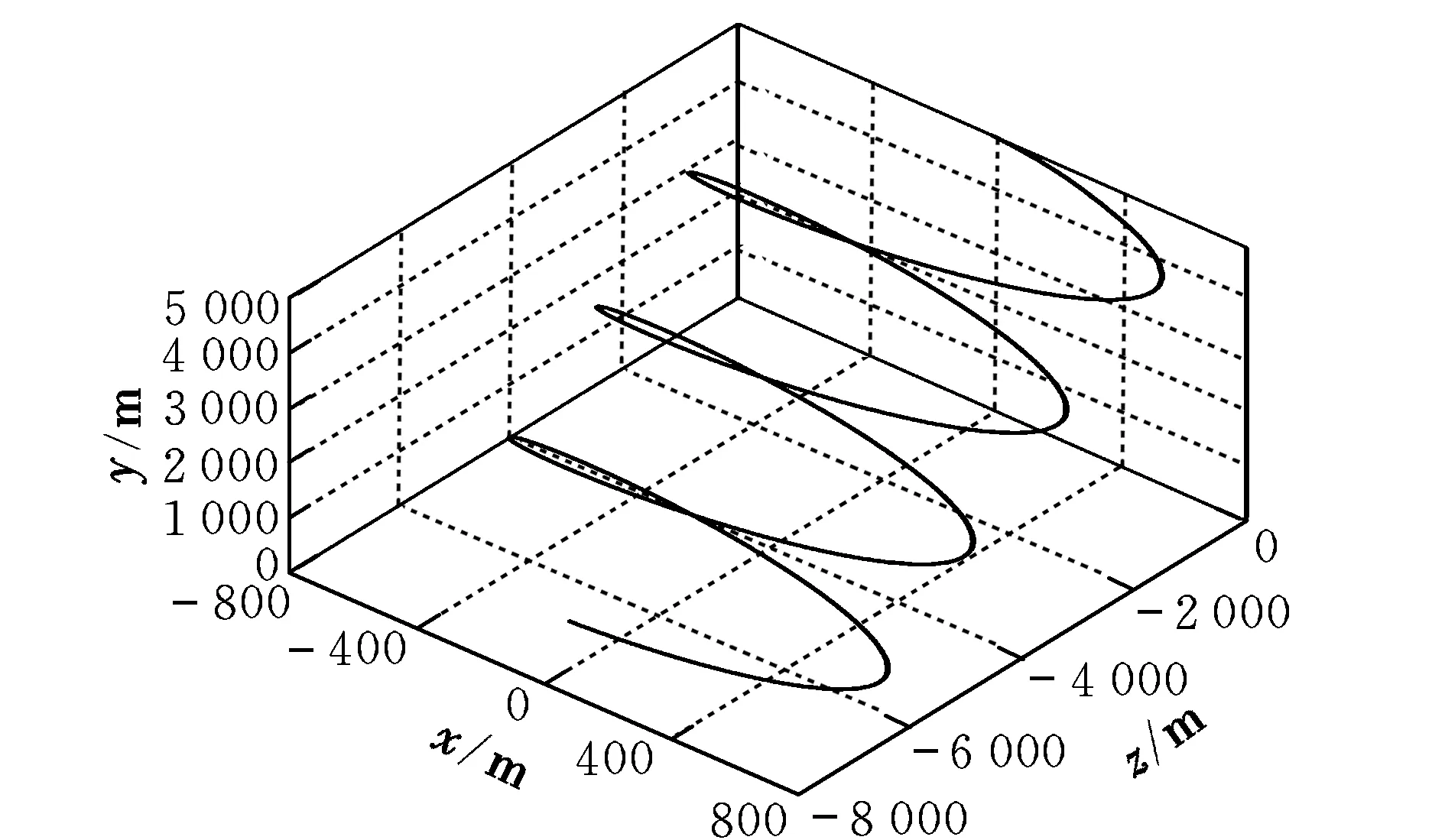
图9 单侧操纵有风时翼伞的飞行轨迹Fig.9 Flight trajectory of the parafoil considering the influence of wind with one-side control

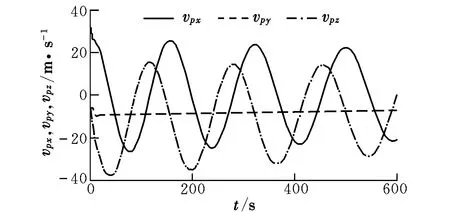
图10 单侧操纵有风时翼伞速度的时间历程Fig.10 Time histories of velocity of the parafoil considering the influence of wind with one-side control

4 结论

通过对以上结果进行分析,可以得到如下关于大型翼伞系统的重要结论:

(1)没有任何操纵时翼伞系统将做稳定滑翔飞行,飞行速度较大,达23～29 m/s。稳定滑翔过程中滑翔比保持不变,但飞行速度缓慢减小,这是由于气动力所做的负功的绝对值大于重力所做的正功所致。此外,由于大型翼伞系统的惯性较大,使得系统对外界的抗干扰能力大大增强。

(2)单侧操纵时翼伞的飞行轨迹为螺旋线,转弯半径和俯仰角均保持不变。与小型翼伞系统相比,大型翼伞系统的转弯半径要大得多,转弯周期也要长得多[1]。

(3)风速和风向均对翼伞系统的飞行轨迹有明显影响,进而改变着陆点的位置,但水平风对翼伞系统的留空时间影响很小。进一步的分析还表明,对于同样的翼伞,初始高度和回收物重量是影响留空时间的主要因素。

[1] 韩雅慧,杨春信,肖华军,等.翼伞精确空投系统关键技术和发展趋势[J].兵工自动化,2012,31(7):1-7.

[2] 王利荣.降落伞理论与应用[M].北京:宇航出版社,1997:528-600.

[3] Nicolaides J D.Parafoil wind tunnel tests[R].AD731564,Indian:University of Notre Dame,1971.

[4] 朱旭,曹义华.翼伞平面形状对翼伞气动性能的影响[J].航空学报,2011,32(11):1998-2007.

[5] Timothy M Barrows.Apparent mass of parafoils with spanwise camber[J].Journal of Aircraft,2002,39(3):445-451.

[6] Nicolaides J D,Tragarz M A.Parafoil flight performance[R].AD7311143,Indian:University of Notre Dame,1971.

[7] Prakash Om,Daftary Avani.Trim and stability analysis of parafoil/payload system using bifurcation methods [C]//18th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar.Munich Germany:AIAA,2005.

[8] Prakash Om,Ananthkrishnan N.Modeling and simulation of 9-DOF parafoil-payload system flight dynamics[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit.Keystone,Colorado:AIAA,2006.

[9] Lingard J S.Precision aerial delivery seminar ram-air parachute design[C]//13th AIAA Aerodynamic Decelerator Systems Technology Conference. Clearwater Beach:AIAA,1995.

[10] Slegers Nathan,Costello Mark.Aspects of control for a parafoil and payload system[J].Journal of Guidance,Control,and Dynamics,2003,26(6):898-905.

[11] 熊菁. 翼伞系统动力学与归航方案研究[D].长沙:国防科学技术大学,2005.

[12] 熊菁,秦子增,程文科.翼伞系统自动归航轨迹的设计[J].中国空间科学技术,2005,25(6):51-59.

[13] Wise Kevin A.Dynamics of a UAV with parafoil under powered fligh [C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Keystone,Colorado:AIAA,2006.

[14] 张俊韬,侯中喜.动力翼伞系统纵向动力学建模研究[J].系统仿真学报,2010,22(11):2541-2544.

[15] 钱克昌,陈自力.动力翼伞非线性动力学建模与仿真[J].计算机仿真,2011,28(12):9-13.

[16] 洪嘉振.计算多体系统动力学[M].北京:高等教育出版社,1999:202-326.

[17] 卢惠民.飞行仿真数学建模与实践[M].北京:航空工业出版社,2007:178-180.

(编辑：姚妙慧)

Flight simulation of large parafoil-payload systems based on multibody dynamics

CHEN Jian-ping, NING Lei-ming, ZHANG Hong-ying, TONG Ming-bo

(College of Aerospace Engineering, NUAA, Nanjing 210016, China)

Flight dynamic analysis is important for design and homing project research of large parafoil-payload systems. In order to do this, a new method based on the theory of multibody dynamics is presented. A multibody system consisting of a fixed-shape parafoil canopy and a payload body is given. The kinematic constraint equations and flight dynamic equations obeyed by a large parafoil-payload system are derived. By introducing Lagrangian multipliers, the closed flight dynamic equations of a large parafoil-payload system are developed in detail with the application of the theory of dynamics of multibody systems. And the obtained equations are used to compute the flight response of a large parafoil-payload system. The computational results show that, compared with small parafoil-payload systems, large parafoil-payload systems have some features such as higher steady glide speed, stronger anti-interference ability, longer turning flight radius, longer turning flight period and slower controlling response. In addition, there are obvious effect of wind speed and wind direction on flight trajectory and landing point of large parafoil-payload systems. For the same parafoil, payload and initial height are the main factors influencing the stay time of the system in the air. The method in this paper can be applied to flight dynamic simulation of large parafoil-payload systems efficiently and accurately.

parafoil-payload system; flight dynamics; multibody system; dynamic modeling; numerical simulation

2015-03-10;

2015-08-09;

时间:2015-08-17 11:04

国家自然科学基金资助(11002070)；航空科学基金资助(2012ZC52035)

陈建平(1963-)，男，江苏泰州人，教授，博士，研究方向为多体系统动力学、飞行力学、航天返回与回收。

V212.1

A

1002-0853(2015)06-0486-05