基于改进GPC的无人直升机动态路径规划
2015-03-15翟文鹏齐莉吴昊马兰
翟文鹏, 齐莉, 吴昊, 马兰
(中国民航大学 空中交通管理学院,天津 300300)
基于改进GPC的无人直升机动态路径规划
翟文鹏, 齐莉, 吴昊, 马兰
(中国民航大学 空中交通管理学院,天津 300300)
针对小型无人直升机航迹受到风场扰动和导航系统定位误差影响下的航迹最优规划问题,建立了风扰动和导航误差影响下的飞行航迹线性模型。基于混合整数规划思想,采用粒子滤波改进广义模型预测控制算法实时规划航迹,降低了导航定位误差造成的航迹估计偏差,提高了航迹估计精度。仿真结果表明,该算法能够生成三维可行航迹并躲避障碍物,且规划时间和无人机能耗较传统方法显著减少。
无人机;航迹规划;粒子滤波;广义预测控制;混合整数规划
0 引言
无人直升机机动性好,具有垂直起降和悬停功能,适合在复杂多变和障碍物较多的飞行环境中执行任务。在已知障碍物的情况下,无人机要实现自主飞行,需要具有在满足约束条件情况下实时最优航迹规划的能力[1-2]。航迹规划是无人机任务规划的关键技术之一[3],目前针对无风情况下的无人机航迹规划研究较多,而对于风场中的规划研究相对较少。
无风情况下,模型预测控制算法已经应用于无人机航迹规划,算法能够进行在线规划,并得到控制输入量。通过将威胁区、速度、加速度以及威胁规避等约束条件转化为能够直接应用于MILP中的形式,并结合模型预测控制方法进行规划以满足实时性要求,即基于混合整数线性规划无人机实时航迹规划。加入任务对飞行时间的约束条件,通过控制飞行器的航向和速度,使其有效规避地形障碍和雷达威胁[4],并在预定时间到达目标点或新任务中的新目标点,从而将三维路径规划拓展到四维空间中去。文献[5]针对某小型无尾飞翼布局无人机,运用CFD方法分析了该无人机的气动特性,计算了气动导数及操纵导数,建立了模型预测控制算法的仿真模型,并运用动态矩阵控制算法设计了飞行控制系统。
对于风场中的无人机路径规划研究主要有:黄华等[6]对低空风场进行建模,并定量评估了风场扰动对无人机导航系统的影响;文献[7-8]讨论了微型无人机的航迹规划中常值风的影响问题。上述研究仅考虑了常值风对航迹的影响,没有解决在导航定位误差存在情况下的航迹实施规划问题。
在假设不考虑飞行环境中的气象风和导航定位误差的情况下,无人机规划航迹与实际飞行航迹产生偏差。根据有偏差的航迹,通过模型预测控制算法得到的控制变量易造成误动作,使得无人机耗能增加,甚至影响飞行安全。本文针对上述问题,建立无人机随机状态方程,以粒子滤波算法(PFA)改进广义模型预测控制算法在在线估计飞行器航迹的基础上规划飞行航迹。该方法降低了规划航迹的能耗,提升了飞行安全性。
1 模型建立
1.1 无人直升机运动方程
有学者指出,飞行过程中目标航迹与理想航迹的误差服从标准正态分布。在实际飞行过程中,受气象风以及雷达或卫星定位观测误差的影响,造成实际飞行轨迹与理想轨迹之间存在误差。为了分别反映这些误差对飞行造成的影响,量化这些影响造成的飞行轨迹误差,产生更加符合实际的航迹数据,需要在以往简单模拟的飞行轨迹模型中加入这些不确定性数据,使其更加符合实际情况。
天气情况作为随机因素,是影响飞机位置的主要外部因素之一,误差服从均值为3、标准差σf=3 m的标准正态分布[9]。另一个影响飞机位置的随机因素是导航误差,本文假设飞机的定位信息由基于卫星导航的定位系统完成。北斗二代导航误差服从均值为0、标准差σp=10 m的标准正态分布[10]。将上述两个随机误差项引入质点运动学模型得到符合实际情况的飞行模型,并将飞机质点三维坐标提取出来。模型可表示为:
(1)

Yk=Yk-1+VΔt+0.5a(Δt)2
(2)

1.2 约束条件
(1)直升机爬升/下降的速度和加速度约束限制可表示为:
(3)
(2)避障约束: 避免撞到障碍物的约束可以通过引入逻辑变量和M法表示为逻辑变量和连续变量的混合决策变量的线性约束。障碍物表示为:
{(xyz)∈R3:xmin≤x≤xmax,
ymin≤y≤ymax,zmin≤z≤zmax}
(4)
约束可表示为:
(5)
式中:bkj∈{0,1}(j=1,2,…,6)。
2 最优路径求解算法
广义预测控制(GPC)是在自适应控制的研究中发展起来的一类预测控制算法[11],在系统受到外界环境干扰的情况下,能够保证控制精度和系统稳定。被控对象的数学模型采用受控自回归积分滑动平均模型CARIMA方程描述:
A(z-1)yk=B(z-1)uk-1+C(z-1)ξk/Δ
(6)
式中:A(z-1),B(z-1)和C(z-1)为后移算子z-1的多项式;uk-1和yk分别为被控对象的输入和输出;Δ=1-z-1为差分算子;ξk为白噪声序列。在广义预测控制中,k时刻的优化性能指标具有以下形式:
(7)
式中:E为数学期望;w为对象输出的期望值,此值经过柔化处理;N1和N2分别为优化时域的始值与终值;NU为控制时域;λj为控制加权系数。根据滚动优化原则最小化目标函数J,得到控制律为:
uk=uk-1+gT(w-f)
(8)

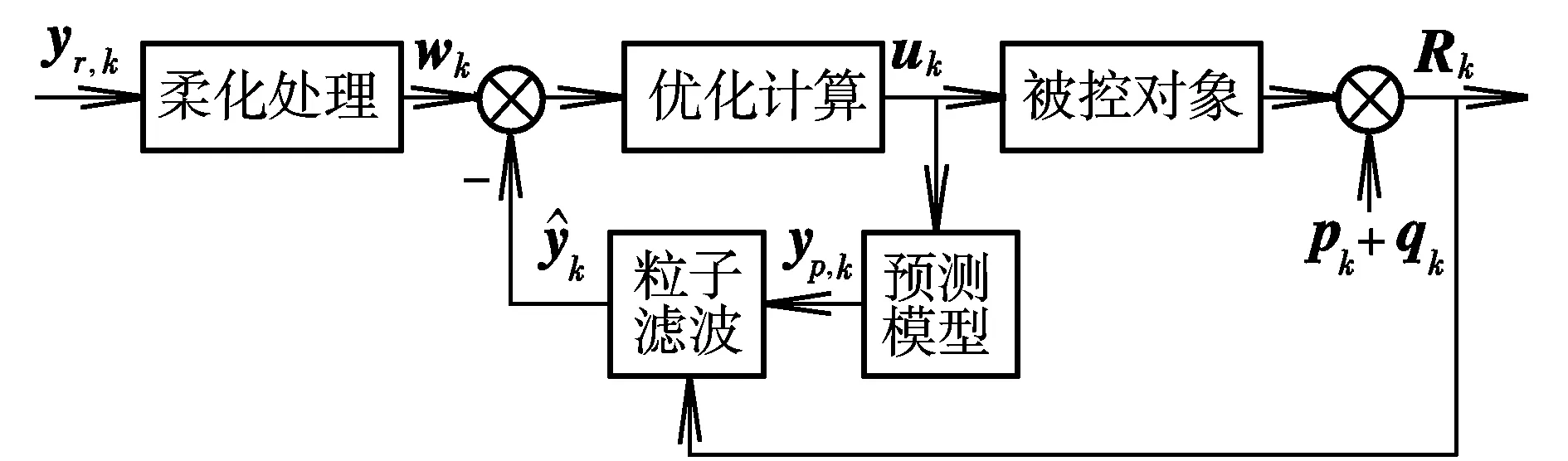
图1 广义预测控制原理图Fig.1 Schematic of GPC
蒙特卡洛模拟方法利用所求状态空间中大量的样本点来近似逼近待估计变量的后验概率分布,从而将积分问题转换为有限样本点的求和问题。PF的核心思想便是利用一系列随机样本的加权和表示后验概率密度,通过求和来近似积分操作。
标准的PF流程为[12]:
(1) 粒子集初始化,k=0。

(2) 对于k=1,2,…,N循环执行以下步骤:

3 仿真验证及结果分析
针对小型无人机进行仿真,初始悬停位置为O(71,-53,4)m,目标悬停位置为D(80,50,20)m。无人机飞行参数为:vxmax=vymax=13 m/s,axmax=aymax=2 m/s2,vzmax=2 m/s,azmax=1 m/s2;规划时域T=10 s,Δt=1 s,M=10 000,N=6,λ=0.01,c=1。这里假设导航误差和风速误差均服从均值为0、标准差为1的正态分布。
由于存在导航误差和风速造成的位置偏差,无人机需克服这两种偏差造成的航迹偏差。图2为未通过粒子滤波估计航迹得到的航迹。
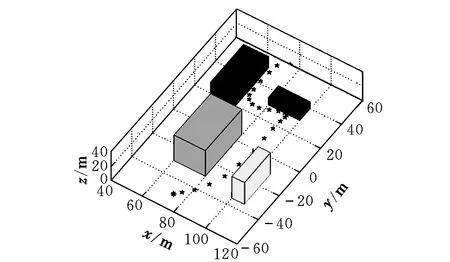
图2 传统方法航迹规划结果Fig.2 Flight path planning results with traditional method
基于GPC的混合整数规划问题通过MATLAB调用CPLEX求解,得到最优轨迹如图3所示。可以看出,两个航迹终点基本达到目标,但所需时间和最终航迹位置偏差差距明显。

图3 改进方法航迹规划结果Fig.3 Flight path planning results with improved method
表1为经过500次仿真验证的航迹规划结果。由于加速度决定了无人机速度改变量,所以三轴加速度平方和反映了燃油消耗量。三轴加速度平方和相比于传统方法分别降低了12.8%,1.5%和5.3%。传统算法的试验结果说明误动作造成的燃油消耗大于本文提出的算法。另外,采用本文提出的算法规划的航迹终点与目标点一致性较好,同时无人机到达目标点的时间缩短了2 s。
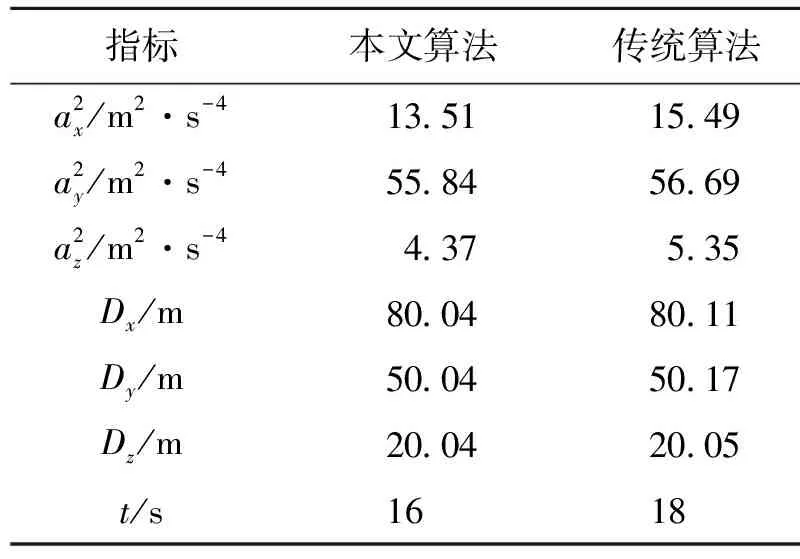
表1 仿真试验结果对比Table 1 Comparison of the simulation results
4 结束语
本文在前人研究成果的基础上,考虑导航误差和风速误差造成的实际航迹误差,利用粒子滤波改进了基于广义预测的航迹规划算法。试验结果表明,该算法提高了航迹规划精度、减少了耗油量,验证了算法的有效性。接下来,还需要继续研究在无人机冲突避让情况下的规划最优路径算法,提高无人机的生存率,为无人机的广泛应用提供理论方法。
[1] Zheng C W,Xu F J,Hu X H,et al.Online route planner for unmanned air vehicle navigation in unknown battlefield environment[C]//Computational Engineering in Systems Applications,IMACS Multi Conference.Piscataway,USA:IEEE,2006:814-818.
[2] 陈洋,赵新刚,韩建达.移动机器人三维路径规划方法综述[J].机器人,2010,32(4):568-576.
[3] 张艳, 高晓光, 魏小丰. 四维空间中的无人机动态路径规划及仿真[J].系统仿真学报, 2009,21(24):7838-7841.
[4] 屈晓波, 李中健, 章卫国. 模型预测控制算法在飞翼无人机中的应用研究[J].测控技术, 2013, 32(3):57-61.
[5] 郝震, 张健, 朱凡, 等. 雷达威胁环境下的无人机三维航迹规划[J].飞行力学, 2010,28(1): 47-52.
[6] 黄华, 陆汉城, 徐幼平, 等. 风场扰动对无人机控制/导航影响效应仿真[J]. 解放军理工大学学报: 自然科学版, 2012, 13(5):565-570.
[7] Ceccarelli N,Enright J J,Frazzoli E,et al.Micro UAV path planning for reconnaissance in wind [C]//Proceedings of the 2007 American Control Conference. New York: IEEE,2007:5310-5315.
[8] McGee T G,Spry S,Hedrick J K.Optimal path planning in a constant wind with a bounded turning rate[C]//2005 AIAA Conference on Guidance,Navigation,and Control.San Francisco:AIAA,2005:3456-3466.
[9] Jackson M R,Zhao Y J.Sensitivity of trajectory prediction in air traffic management[J].Journal of Guidance,Control,and Dynamics,1999,22(2):219-228.
[10] Herencia-Zapana H,Hagen G,Neogi N.A framework for probabilistic evaluation of interval management tolerence in the terminal radar control area[C]//Digital Avionics Systems Conference (DASC),2012 IEEE/AIAA 31st.Williamsburg:IEEE,2012:9E1-1-9E1-8.
[11] 邓丽,黄炎,费敏锐,等.改进的广义预测控制及其在温度系统中的应用[J].仪器仪表学报, 2014,35(5):1057-1064.
[12] 杨旭,程杨,曹喜滨.粒子滤波在卫星轨道确定中的应用[J]. 控制理论与应用,2005,22(4):573-577.
(编辑:李怡)
Unmanned helicopter dynamic flight path planning based on improved generalized prediction control method
ZHAI Wen-peng, QI Li, WU Hao, MA Lan
(College of Air Traffic Management, Civil Aviation University of China, Tianjin 300300, China)
A linear model and flight path optimal planning of small unmanned helicopter effected by wind turbulence and errors on navigation system was established. Based on mix integer linear programming of generalized predictive control (GPC) which was improved by particle filter, the method decreased flight path error caused by navigation system, and the flight path estimation precision was increased. Simulation results show that the method is able to generate a three-dimensional feasible flight track and avoid obstacles, and the planning time and energy consumption is significantly less than that with traditional methods.
UAV;flight path planning;particle filter;generalized predictive control;mix integer linear programming
2014-08-13;
2014-12-20;
时间:2014-12-15 08:32
国家自然科学基金资助(71171190,61179042,U1333116);中央高校基本科研经费资助(ZXH2012M003);中国民航大学科研启动基金资助(2012QD02X);大学生创新创业训练计划资助(201410059082)
翟文鹏(1985-),男,天津人,讲师,博士,研究方向为空中交通规划与管理。
V279
A
1002-0853(2015)02-0170-03
