基于动态逆-PID的高超声速飞行器巡航姿态控制
2015-03-15吴雨珊江驹甄子洋顾臣风
吴雨珊, 江驹, 甄子洋, 顾臣风
(南京航空航天大学 自动化学院, 江苏 南京 210016)
基于动态逆-PID的高超声速飞行器巡航姿态控制
吴雨珊, 江驹, 甄子洋, 顾臣风
(南京航空航天大学 自动化学院, 江苏 南京 210016)
以某型高超声速飞行器为研究对象,针对巡航状态下气动参数不确定的姿态控制问题,提出了一种结合非线性动态逆控制与PID控制的姿态控制方法。首先,对高超声速飞行器非线性模型进行精确反馈线性化,得到了飞行器纵向姿态仿射非线性方程;接着,为速率变化快慢不同的迎角和俯仰角速率分别设计了动态逆控制律以抵消对象的非线性特性;然后,在动态逆控制的基础上,采用工程上易于实现的PID控制补偿由于未精确建模带来的系统逆误差,实现了迎角对指令信号的有效跟踪;最后,进行了数值仿真验证。结果表明,所设计的高超声速飞行器动态逆-PID姿态控制器具有良好的跟踪性能和鲁棒性能。
高超声速飞行器; 姿态控制; 非线性动态逆控制
0 引言
高超声速飞行器是指飞行马赫数大于5的临近空间飞行器。高超声速飞行器在巡航飞行过程中要求控制器具有较高的姿态控制精度,然而,由于高超声速飞行器具有较强的非线性和严重的耦合性,给姿态控制带来了很大难度,因此设计一种控制性能好、精度高的姿态控制器显得尤为重要。
传统飞行器姿态控制通常采用小扰动线性化方法,难以适用于高度非线性的高超声速飞行器。目前有关高超声速飞行器控制方法的研究文献主要集中在非线性控制方面,比如文献[1]利用反馈线性化为高超声速飞行器设计了纵向反馈控制律,文献[2]将高超声速飞行器的耦合项用非匹配不确定性的形式表示,并设计了滑模变结构控制器,文献[3]为高超声速飞行器设计了二阶滑模控制器,文献[4]实现了基于回馈递推方法的近空间飞行器鲁棒自适应控制。
动态逆方法是一种有较强适应性和通用性的非线性控制方法,设计过程中避免了增益控制、自适应控制等方法中存在的大量调参工作。然而,动态逆控制对系统建模误差较为敏感,当气动参数存在不确定时,采用动态逆设计的飞行控制系统将呈现较差的控制性能[5]。如何提高动态逆控制系统的鲁棒性,研究者们也提出了一些处理方法,但这些方法往往比较复杂,工程上较难实现。
为此,本文从某型高超声速飞行器的非线性方程入手,利用精确反馈线性化得到飞行器姿态仿射非线性方程,再根据时标分离原则将飞行器纵向姿态控制分解为迎角慢回路和俯仰角速率快回路,分别设计动态逆控制律。考虑到气动参数存在不确定性对动态逆控制效果的影响,本文采用工程上易于实现的PID方法对层叠结构控制器进行校正,最后通过数值仿真进行了验证。
1 高超声速飞行器建模
1.1 非线性数学模型
某高超声速飞行器在高超声速巡航飞行条件下的纵向运动模型描述为[6-7]:
(1)
(2)

(3)
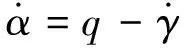
(4)
(5)
气动力和力矩表示为:
L=0.5ρV2sCL
(6)
D=0.5ρV2sCD
(7)
Myy=0.5ρV2sc[CM(α)+CM(δe)+CM(q)]
(8)
式中,气动导数CL,CD,CM(α),CM(q)及CM(δe)由以下巡航飞行条件下的经验公式所得:
CL=0.6203α
(9)
CD=0.6450α2+0.0043378α+0.003772
(10)
CM(α)=-0.035α2+0.036617α+5.3261×10-6
(11)
CM(q)=(c/2V)q(-6.796α2+0.3015α-0.2289)
(12)
CM(δe)=Cm(δe-α)
(13)
发动机推力计算公式为:
T=0.5ρV2sCT
(14)
式中:CT为推力系数, 且
(15)
发动机动态方程采用二阶系统模型:
(16)
式中:β为发动机节流阀调定值;βc为油门开度,且为常量。
假设在高超声速巡航飞行状态下,高超声速飞行器的质量m、俯仰力矩惯性积Iyy、飞机表面积s、翼弦长c存在摄动,采用所假定的额定值附加一个变化来表示参数的不确定性,即:
m=m0(1+Δm)
(17)
Iyy=I0(1+ΔI)
(18)
s=s0(1+Δs)
(19)
c=c0(1+Δc)
(20)
1.2 精确反馈线性化
考虑高超声速飞行器巡航飞行状态下,其速度、高度和发动机推力应为常值,因此控制输入为升降舵偏转δe,状态量为飞行器纵向的两个姿态变量:迎角α和俯仰角速率q,即x=[qα]T。现利用精确反馈线性化得到飞行器纵向姿态仿射非线性方程,表示为:

(21)
2 动态逆姿态控制器的设计
直接应用动态逆方法的前提条件为被控对象的控制变量和状态变量的数目相同,以保证系统的逆存在。然而,从上述纵向姿态仿射非线性方程看出,式(21)表示的飞行器是利用一个操纵面控制两个飞行姿态变量。因此,为了将非线性动态逆控制方法应用到飞行控制系统中,需要根据系统状态的响应速度将系统状态分成两个回路,分别利用动态逆控制方法设计飞行控制系统。
本文研究的高超声速飞行器俯仰角速率变化很快,相对而言迎角的变化较慢,采用直接逆的方法进行控制器设计会将俯仰角的快速变化引起的扰动带入到系统中,且由于控制输入只有一个,因此将q和α分别作为快、慢两个回路进行控制器设计。
高超声速飞行器的动态逆控制器结构如图1所示。

图1 高超声速飞行器动态逆控制器结构图Fig.1 Dynamic inversion controller of the hypersonic vehicle
2.1 快回路控制器的设计
由式(21)可得,快回路表示为:
(22)
对快回路的俯仰角速率取动态逆反馈律为:
(23)
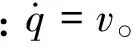
2.2 慢回路控制器的设计
慢回路在快回路的外层,由慢状态构成,其输入为理想二阶系统产生的指令信号αc,输出为快回路的输入信号,即期望角速率qc。由式(21)可将慢回路表示为:
对慢回路的迎角取动态逆反馈律为:

3 动态逆-PID姿态控制器设计
从以上动态逆控制器的设计过程中可以看出,动态逆控制器的高性能是建立在对控制对象精确建模、精确求解逆过程以及各状态量实时值测量精确的基础上。然而,对于高超声速飞行器而言,部分状态变量难以测得,外界的环境变化剧烈,气动参数不确定性对系统的影响较大,式(17)~式(20)为本文研究的高超声速飞行器气动参数不确定性的具体表达式。

忽略俯仰角速率回路的影响,采用PID控制后使得迎角回路输入输出特性满足:
式中:KD,KP,KI为需要调节的微分、比例、积分因子。
取飞行器迎角响应的参考模型为:
式中:Ω为放大系数;ωn为参考模型的自然频率;ζn为阻尼系数。
高超声速飞行器的动态逆-PID控制器结构如图2所示。通过调节PID控制的比例、积分及微分因子,使高超声速飞行器在气动参数摄动较大时仍保持良好的鲁棒性能。

图2 高超声速飞行器动态逆-PID控制器结构图Fig.2 Dynamic inversion-PID controller of the hypersonic vehicle
4 仿真研究
以某高超声速飞行器为例,对高超声速飞行器的姿态控制回路进行仿真研究,以验证所设计的姿态控制器的性能。初始仿真条件为:Ma=7,H=23 km,α=0 rad,q=0 rad/s。
4.1 动态逆姿态控制器
在无参数摄动、气动导数不变的条件下,采用第2节所设计的动态逆姿态控制器的仿真结果如图3和图4所示。

图3 α随时间的响应曲线Fig.3 α response versus time

图4 q随时间的响应曲线Fig.4 q response versus time
由仿真结果可以看出,在被控对象精确建模的基础上,动态逆控制器具有良好的跟踪性能。然而,考虑到高超声速飞行器飞行包线大,环境复杂且变化剧烈,为此加入如下干扰:飞机质量m、飞机表面积Sw、翼弦长c均摄动+20%;气动导数CL和Cmα均摄动+20%。采用动态逆姿态控制器的纵向姿态响应结果如图5和图6所示。

图5 参数摄动+20%时α随时间的响应曲线Fig.5 α response versus time with+20% parameter perturbation
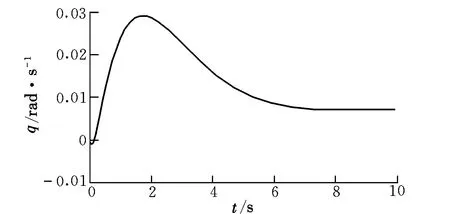
图6 参数摄动+20%时q随时间的响应曲线Fig.6 q response versus time with+20% parameter perturbation
由上图可知,加入干扰后,仅靠动态逆控制器不能保证良好的跟踪信号,迎角响应曲线与指令信号出现较大偏差。
4.2 动态逆-PID姿态控制器
针对含扰动的高超声速飞行器,为提高飞行控制系统的鲁棒性能,下面采用本文第3节所设计的动态逆-PID姿态控制器,得到α和q的响应曲线,如图7和图8所示。其中,PID控制参数通过多次试验选取为KP=2,KI=0.5,KD=4。

图7 α随时间的响应曲线Fig.7 α response versus time

图8 q随时间的响应曲线Fig.8 q response versus time
由仿真结果可见,采用动态逆-PID控制器,参数摄动仅会使迎角产生量级为10-4rad的波动,显示出良好的鲁棒性能。可以看出,所设计的非线性动态逆-PID姿态控制器能够使飞行姿态均在较短的时间内达到期望值,并且无稳态误差,能够较好地实现姿态角度的跟踪;消除了快速变化的俯仰速率回路对迎角回路的影响,并使得俯仰速率变化平稳,同时系统能够快速准确地跟踪参考指令信号,能抵制外部环境使参数波动对系统的影响,具有良好的动态性能和鲁棒性能。
5 结束语
本文针对具有强非线性、不确定性的高超声速飞行器姿态控制问题,设计了一种动态逆姿态控制器和动态逆-PID姿态控制器。首先,利用精确反馈线性化得到飞行器纵向姿态仿射非线性方程,再利用时标分离原则,将模型分为慢回路运动和快回路运动,分别进行了动态逆控制器设计。然后,考虑到气动参数的不确定性会使动态逆姿态控制精度降低,本文采用工程上易于实现的PID方法对动态逆层叠结构控制器进行校正。最后,在高超声速巡航飞行条件下进行了仿真验证。仿真结果表明,本文设计的动态逆-PID姿态控制器具有较满意的姿态控制效果和鲁棒性能。
[1] 曹建,张平.采用扩展线性化方法设计高超声速飞行器飞控系统[C]//第13届中国系统仿真技术及其应用学术年会论文集.安徽合肥:中国科学技术大学,2011:995.
[2] 周凤岐,王延,周军,等.高超声速飞行器耦合系统变结构控制设计[J].宇航学报,2011,1(32):67-69.
[3] 王洪欣,江驹,杜洁,等.高超声速飞行器二阶滑模控制器设计[J].新型工业化,2014,3(3):38-43.
[4] 周丽.基于回馈递推方法的近空间飞行器鲁棒自适应控制[D].南京:南京航空航天大学,2008.
[5] 赵刚.高超声速飞行器神经网络动态逆姿态控制器设计[J].系统仿真技术, 2010,6(4):308-311.
[6] Wang Q,Stengle R F.Robust nonlinear control of a hypersonic aircraft[C]//AIAA Guidance,Navigation and Control Conference.Reston,USA:AIAA,1999:413-423.
[7] Marrison C I,Stenge R F.Design of robust control systems for a hypersonic aircraft[J].Journal of Guidance,Control,and Dynamics,1998,21(1):58-63.
(编辑:姚妙慧)
Dynamic inversion-PID based cruising attitude control of hypersonic vehicle
WU Yu-shan, JIANG Ju, ZHEN Zi-yang, GU Chen-feng
(College of Automation Engineering, NUAA, Nanjing 210016, China)
This paper takes a nonlinear longitudinal model of a hypersonic vehicle as the object. One nonlinear dynamic inversion control method combined with PID control was put forward to deal with the uncertainty of hypersonic aerodynamic parameters. Firstly, the precise linearization equation was obtained from the nonlinear flight model. Next, the fast and slow subsystems were separated. The dynamic inversion control law was designed for each subsystem to offset the nonlinear part. Then, the engineering easy-realized PID control theory was used to compensate the system inversion error. Finally, the dynamic inversion-PID controller is shown to have good dynamic responses and robustness.
hypersonic vehicle; attitude control; nonlinear dynamic inversion control
2014-08-07;
2014-11-17;
时间:2014-12-15 08:37
国家自然科学基金资助(61304223);教育部高等学校博士科学点专项科研基金(20123218120015);南京航空航天大学研究生创新基地(实验室)开发基金资助(kfjj201420);中央高校基本科研业务费专项资金资助
吴雨珊(1990-),女,四川成都人,硕士研究生,研究方向为飞行器控制; 江驹(1963-),男,江苏扬州人,教授,博士生导师,研究方向为飞行器控制、智能控制、机器学习等。
V249.1
A
1002-0853(2015)02-0145-05
