常利率带干扰的两类相关理赔风险模型

贺小丽，余国胜*，姚 钲，姚春临，陈华斌

（1.江汉大学 数学与计算机科学学院，湖北 武汉 430056；2.南昌大学 理学院，江西 南昌 330031）

常利率带干扰的两类相关理赔风险模型

贺小丽1，余国胜*1，姚 钲1，姚春临1，陈华斌2

（1.江汉大学 数学与计算机科学学院，湖北 武汉 430056；2.南昌大学 理学院，江西 南昌 330031）

考虑了保费收取为Poisson-Geometric过程，常利率环境条件下带干扰的两类相关理赔风险过程，把相关的两类理赔计数过程转换为两个独立的Poisson-Geometric过程和推广的Erlang（n）过程，并给出其折现罚金函数所满足的微积分方程。

破产概率；Poisson-Geometric过程；推广的Erlang（n）过程；带干扰；折现罚金函数

0 引言

近年来，保险研究者们开始研究Poisson-Geometric过程，文献［1］针对复合Poisson-Geometric模型首次给出了Gerber-Shiu折现罚金函数满足的更新过程，文献［2］得到了常利率下索赔次数为Poisson-Geo⁃metric过程和Poisson-Geometric折现罚金函数所满足的积分方程。由于保险公司业务种类日益复杂化，保险研究者们对于作为经典风险模型推广的两类理赔相关的风险模型产生了浓厚的兴趣。文献［3］研究了N1(t)=K1(t)+K(t),N2(t)=K2(t)+K(t)，其中K1(t),K2(t)均为Poisson计数过程，K(t)是推广的Erlang（2）过程，讨论了其生存概率。文献［4-5］讨论了两类理赔过程分别是Poisson过程和推广的Erlang（2）过程的风险模型。文献［6］在文献［4-5］的基础上引入了红利的因素。文献［7］将文献［4-5］中的Erlang（2）计数过程推广到Erlang（n）过程。文献［8］讨论了带干扰的两类理赔风险模型，两类理赔的计数过程分别为独立的Poisson过程和广义Erlang（n）过程，得到了此模型的折现罚金函数的Laplace变换。文献［9］研究了带干扰的两类相关理赔风险过程，把相关的两类理赔计数过程转换为两个独立的Poisson-Geometric过程和Erlang（n）计数过程，给出其折现罚金函数所满足的微积分方程及其Laplace变换。它们均不带利率，此外，保费收取有时为Poisson-Geometric过程。本文拟研究保费收取为Poisson-Geometric过程，常利率环境条件下带干扰的两类相关理赔风险过程，把相关的两类理赔计数过程转换为两个独立的Pois⁃son-Geometric计数过程和推广的Erlang（n）过程，得到了其折现罚金函数所满足的微积分方程。

1 风险模型

2 预备知识及引理

3 罚金函数的积分-微分方程

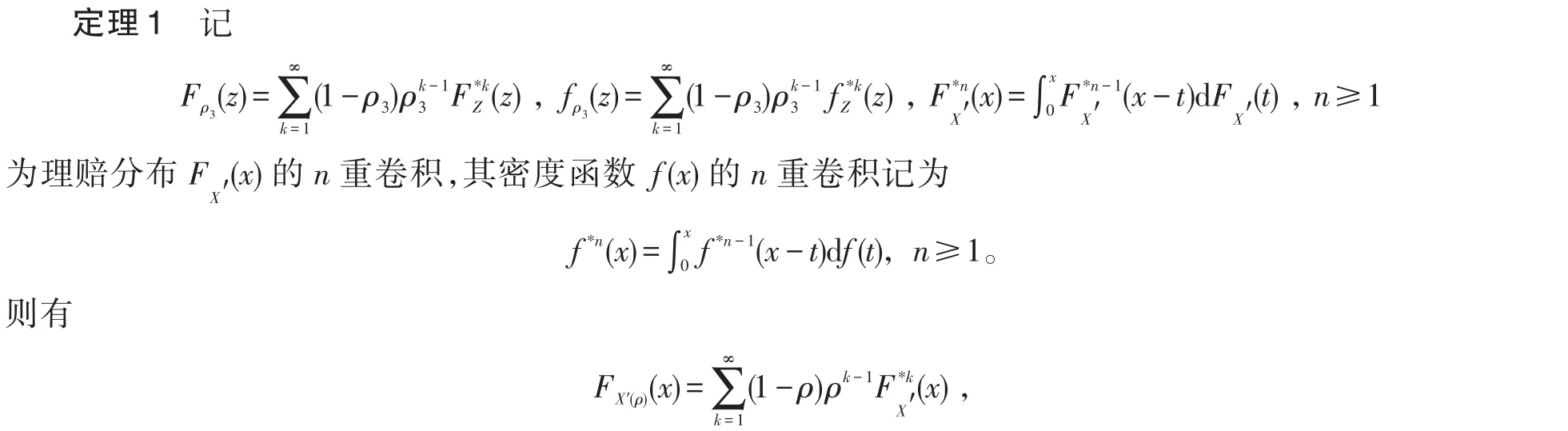
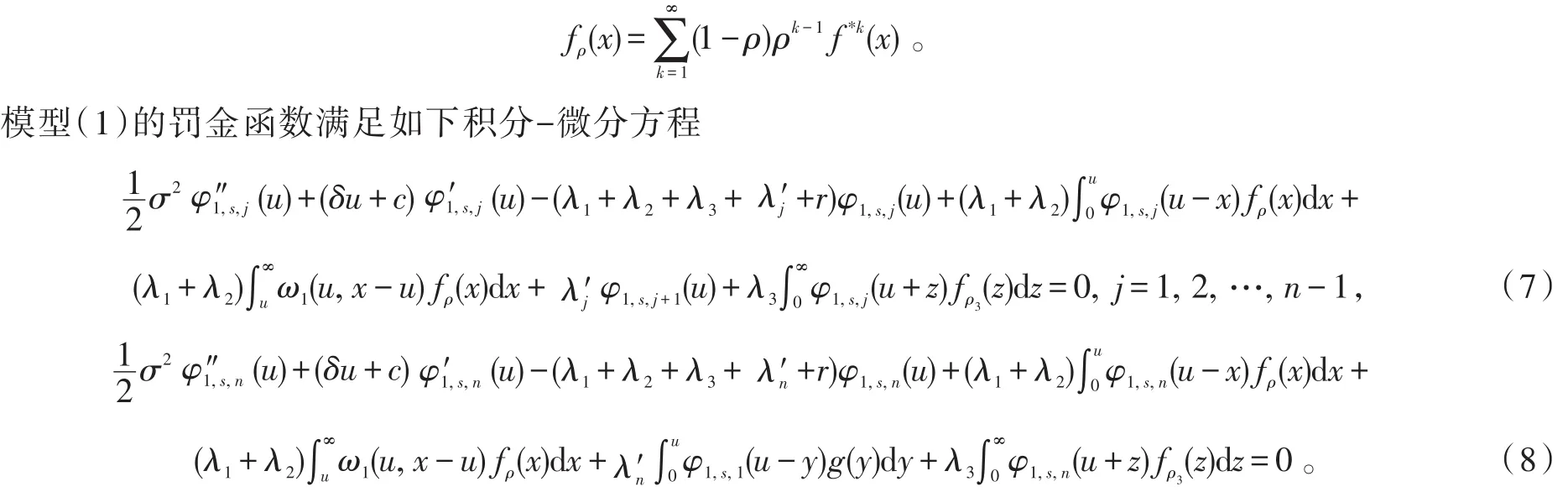
证明设开始时处于状态j（j=1,2,…,n-1）,对充分小的时间h,考虑(0,h]内风险模型的情况，可以分成以下8种情况：①无保费收入，第一类理赔险种没有理赔，第二类理赔险种没有发生状态转移；②无保费收入，第一类理赔险种发生理赔，第二类理赔险种没有发生状态转移；③无保费收入，第一类理赔险种没有理赔，第二类理赔险种发生状态转移；④无保费收入，第一类理赔险种发生理赔，第二类理赔险种发生状态转移；⑤有保费收入，第一类理赔险种没有理赔，第二类理赔险种没有发生状态转移；⑥有保费收入，第一类理赔险种发生理赔，第二类理赔险种没有发生状态转移；⑦有保费收入，第一类理赔险种没有理赔，第二类理赔险种发生状态转移；⑧有保费收入，第一类理赔险种发生理赔，第二类理赔险种发生状态转移。记

（References）

［1］廖基定，龚日朝，刘再明，等.复合Poisson-Geometric风险模型Gerber-Shiu折现惩罚函数［J］.应用数学学报，2007，30（6）：1076-1085.

［2］熊双平.索赔次数为复合Poisson-Geometric过程的常利率风险模型的罚金函数［J］.经济数学，2008，25（2）：136-142.

［3］YUEN K C，GUO J，WU X.On a correlated aggregate claims model with Poisson and Erlang risk processes［J］.Insurance：Mathe⁃matics and Economics，2002，31（2）：205-214.

［4］LI S，GARRIDO J.Ruin probabilities for two classes of risk processes［J］.ASTIN Bulletin，2005，35：61-77.

［5］LI S，LU Y.On the expected discounted penalty function for two classes of risk processes［J］.Insurance：Mathematics and Eco⁃nomics，2005，36：179-193.

［6］范庆祝，尹传存.带红利的两类索赔风险模型的Gerber-Shiu函数［J］.工程数学学报，2009，26（1）：51-59.

［7］ZHANG Z，LI S，YANG H.The Gerber-Shiu discounted penalty functions for a risk model with two classes of claims［J］.Journal of Computational and Applied Mathematics，2009，230（2）：643-655.

［8］赵永霞，王春伟.带扰动的两类索赔风险模型的罚金折扣函数［J］.高校应用数学学报，2010，25（3）：263-272.

［9］刘文震，王传玉.带扰动的两类相关索赔风险模型的折现罚金函数［J］.中国科学技术大学学报，2013，43（6）：444-454.

［10］毛泽春，刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率［J］.应用数学学报，2005，28（3）：419-428.

（责任编辑：胡燕梅）

A Diffusion Risk Model with Two Dependent Classes of Risk Processes Under Constant Interest Rate

HE Xiaoli1，YU Guosheng*1，YAO Zheng1，YAO Chunlin1，CHEN Huabin2
（1.School of Mathematics and Computer Science，Jianghan University，Wuhan 430056，Hubei，China；2.School of Science，Nanchang University，Nanchang 330031，Jiangxi，China）

A diffusion risk model which premium obeyed the Poisson-Geometric process with two dependent classes of risk processes under constant interest rate was considered，the correlated two claims in the counting process were transformed through model into independent Poisson-Geometric and generalized Erlang（n）processes.Integro-differential equations were obtained.

ruin probability；Poisson-Geometric process；generalized Erlang（n）processes；interfer⁃ence；discounted penalty function

O211.6

：A

：1673-0143（2015）06-0513-05

10.16389/j.cnki.cn42-1737/n.2015.06.006

2015-08-16

国家自然科学基金资助项目（11401292）；江汉大学博士科研启动经费资助项目（2011021）

贺小丽（1994—），女，研究方向：金融数学。

*通讯作者：余国胜（1980—），男，讲师，博士，研究方向：随机动力系统、金融数学。E-mail：guosyujianghanun@126.com