广义Wick-型随机迁移方程的一类显式解

陈 彦，韦才敏

（1.汕头职业技术学院 自然科学系，广东 汕头 515078；2.汕头大学 数学系，广东 汕头 515063）

广义Wick-型随机迁移方程的一类显式解

陈 彦1，韦才敏2

（1.汕头职业技术学院 自然科学系，广东 汕头 515078；2.汕头大学 数学系，广东 汕头 515063）

在随机分布空间(S)-1上求解广义Wick-型随机迁移方程，并讨论解的性质。首先通过和式型泛函分离变量法，把求解方程约化为线性二阶随机常微分方程（SODE）；然后再对方程SODE依次取两次积分又转化为随机维他里方程，从而获得了一类用级数表示的显式解，并论证此类解是存在的、唯一的和连续的。

泛函分离变量法；随机迁移方程；线性二阶随机常微分方程；显式解

0 引言

在运动介质中弥散的物质迁移可以建模为随机偏微分方程

式中，U(t，x)表示物质在t时刻点x∈D处的集中量；常数表示弥散系数；V(t，x)∈Rd表示介质的速度；K(t，x)∈R表示相对泄漏率；g(t，x)∈R表示物质源比率；物质初始集中量f(x)是已知的实函数［1］。若假设方程（1）的系数至少有一个是随机的，则称此方程为随机迁移方程。近年来，研究者们对方程（1）的求解多以缺项形式或采用方程的某一项含有布朗运动或白噪声的形式来求解。当K(t,x)=g(t,x)=0,V(t,x)=W(x)（d-维白噪声）时，方程（1）叫做湍流介质中物质的迁移模型［2-4］；若d=1，可用Stratonvich积分和Hitsuda-Skorohod积分形式来解释乘积W(x)·∇U(x)［5］；而当d为任意时，GJERDE等［6］取V(t,x)为d-维φ-光滑化白噪声（φ∈S），把积Wφ(x)·∇U(x)解释为Wick积Wφ(x)⋄∇U(x)（仍取K(t,x)=g(t,x)=0），并给出该方程的显式解。若在方程（1）中取V(t,x)=g(t,x)=0时，则变成含有随机位势的热方程。NUALART等［3］在K(t,x)为白噪声情况下，证明了该方程存在着广义韦纳（Wiener）泛函类型的解。而KALLIANPUR等［7］在研究方程（1）时，取V(t,x)、K(t,x)是确定的且g(t,x)是随机的，将其作为污染弥散的模型。后来GJERDE合并了文献［6］和文献［7］研究的两种情况，并把求解方程推广为

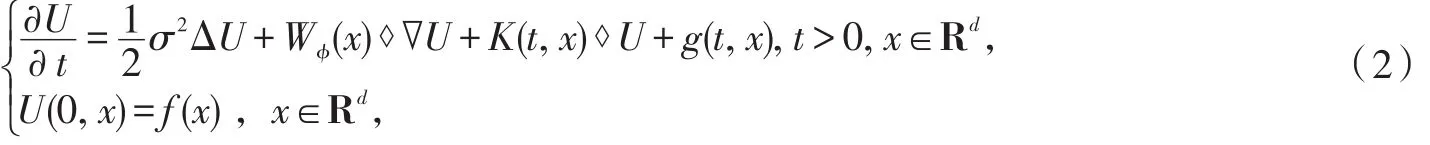
式中，σ为常数，K(t,x)，g(t,x)和f(x)是给定的随机分布过程，且添加了起点概率作为已知条件，从概率角度获得方程（2）的所有解并给出显解公式［8］。

由此可见，GJERDE的求解结果是目前在求解随机迁移方程中较为完善的成果之一。但它仍然是方程（1）取V(t,x)=Wφ(x)时的特殊情况。而对于更一般的情况：即当V(t,x)推广为任意随机过程时，尚未有更进一步的研究。本研究拟在系数V(t,x),K(t,x),g(t,x)和f(x)都是随机的、并添加另一个随机初始值Ut(0,x)作为已知条件的情况下，来探讨方程（1）在Wick积意义下的解。

1 预备知识

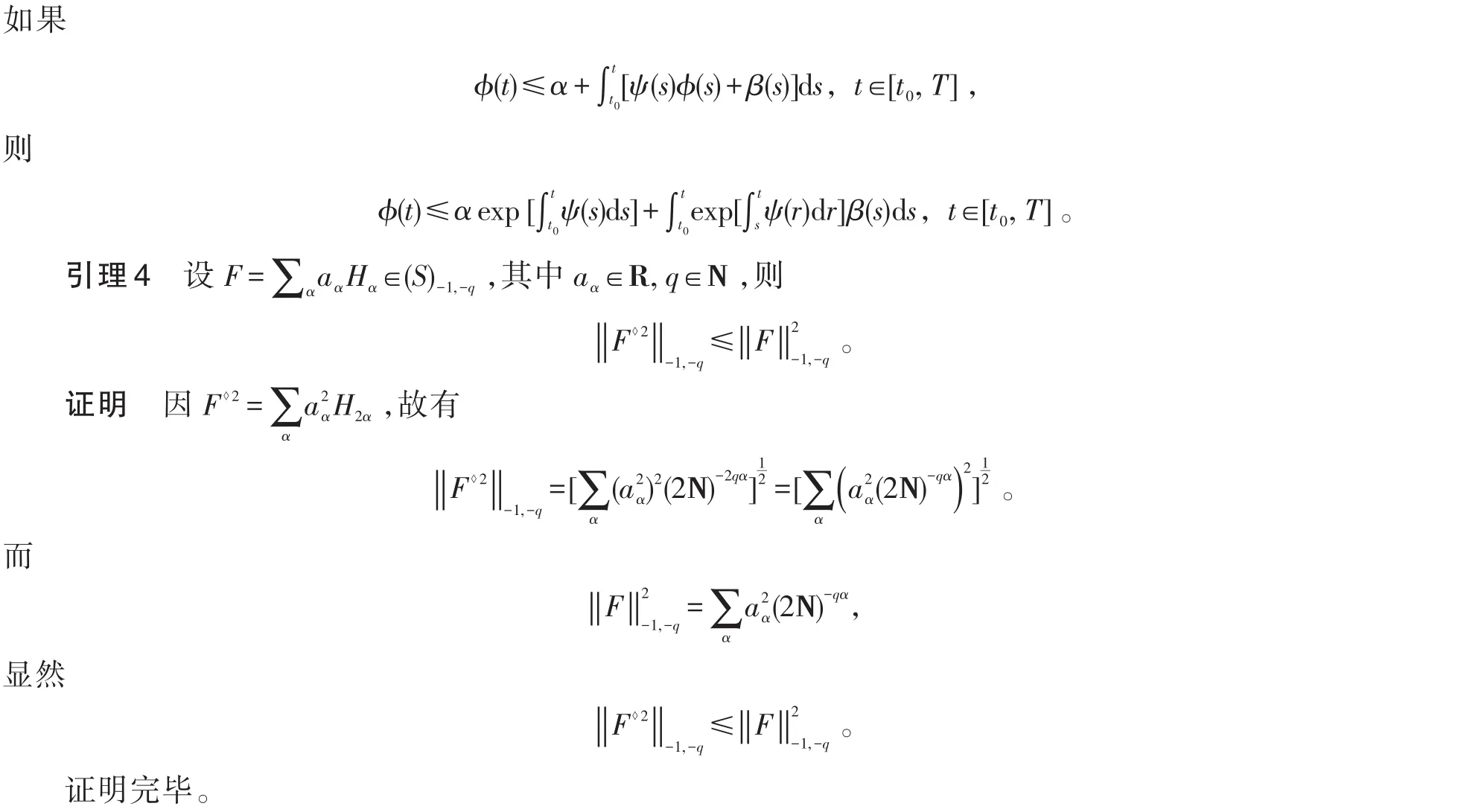
2 广义Wick-型随机移迁方程的一类显式解

3 结论

本文主要给出求解广义Wick-型随机迁移方程的方法途径及解的结果。一开始，该方程除了系数σ为常数外，V(t,x),K(t,x),g(t,x)和f(x)都设为任何随机过程，使求解能在更一般的情况下进行，并添加一个初始数据Ut(0,x)作为已知条件。在求解过程中，主要使用和式型泛函分离变量法及积分法，促使方程进行了两次转化，最终获得了一类(S)-1上的显式解，并论证此类解是存在的、唯一的和连续的；与此同时，又给出了一个确定的辅助函数W(x)，它具有一个很吸引人的性质：即如果能找到若干个W(x)，那么广义Wick-型随机迁移方程就对应有若干个解。但笔者认为这些解应该不是所有的解，而是其中一部分解。那么广义Wick-型随机迁移方程究竟能否导出其他类型的解，甚至所有解？此类问题有待于进一步研究。

（References）

［1］ADOMIAN G，SERRANO S E.Stochastic contaminant transport equation in porous media［J］.Applied Mathematics Letters，1998，11（1）：53-55.

［2］CHOW P L.Generalized solution of some parabolic equations with a random drift［J］.Applied Mathmatics and Optimization 1989，20：81-96.

［3］NUALART D，ZAKAI M.Generalized Brownian functions and the solution to a stochastic partial differential equations［J］.Jour⁃nal of functional Analysis，1989，84：279-296.

［4］POTTHOFF J.White noise methods for stochastic partial equations［J］.Stochastic Partial Differential Equations and Their Appli⁃cations，1992，7：238-251.

［5］POTTHOFF J.White noise approach to parabolic stochastic partial differential equations［J］.Stochastic Analysis and Applica⁃tions in Physics，1994，11：307-327.

［6］GJERDE J，HOLDEN H，ØKSENDALB，et al.An equation modelling transport of a substance in a stochastic medium［J］.Semi⁃nar on Stochastic Analysis，Random Fields and Application，1995，12：123-134.

［7］KALLIANPUR G，XIONG J.Stochastic models of environmental pollution［J］.Advances in Applied Probability，1994，266：377-403.

［8］HOLDEN H，ØKSENDAL B，U VBØE J，et al.Stochastic partial differential equtions［M］.New York：Springer Science+Busi⁃ness Media LLC，2010：165-166，134-135，129.

［9］楼红卫，林伟.常微分方程［M］.上海：复旦大学出版社，2007：114.

［10］娄森岳，唐晓艳.非线性数学物理方法［M］.北京：科学出版社，2006：39.

（责任编辑：胡燕梅）

A Class of Explicit Solutions of Generalized Wick-Type Stochastic Transport Equation

CHEN Yan1，WEI Caimin2
（1.Department of Natural Sciences，Shantou Polytechnic，Shantou 515078，Guangdong，China；2.Department of Mathematics，Shantou University，Shantou 515063，Guangdong，China）

In this paper，we mainly solve the generalized Wick-type stochastic transport equation in the stochastic distributions spaces(S)-1and discuss properties of the solutions.By the sum-type functional separation of variables，the equation is reduced into a linear second-order stochastic ordinary differential equation（SODE），and then the SODE，integrated twice in order，converts to a stochastic Volterra equa⁃tion，so that we obtain a class of explicit solutions in series and argue that the class of solutions are exis⁃tent，unique and continuous.

functional separation of variable；stochastic transport equation；linear second-order stochas⁃tic ordinary differential equation；explicit solution

O175.23

：A

：1673-0143（2015）06-0505-08

10.16389/j.cnki.cn42-1737/n.2015.06.005

2015-07-05

2014年汕头职业技术学院科研课题（SZK2014Y23）

陈 彦（1962—），男，副教授，硕士，研究方向：随机偏微分方程。