有腹筋UHPFRC梁抗剪承载力计算

徐海宾，邓宗才1

（1.工程抗震与结构诊治北京市重点实验室（北京工业大学），100124北京；2.河南理工大学土木工程学院，454003河南焦作）

有腹筋UHPFRC梁抗剪承载力计算

徐海宾1，2，邓宗才1

（1.工程抗震与结构诊治北京市重点实验室（北京工业大学），100124北京；2.河南理工大学土木工程学院，454003河南焦作）

为研究有腹筋UHPFRC梁的抗剪承载力，根据超高性能纤维混凝土梁的剪切破坏机理，结合修正压力场理论，考虑梁上部受压区混凝土和下部受拉区骨料咬合力、箍筋及裂缝间钢纤维共同承受剪力，推导了有腹筋超高性能纤维混凝土梁的抗剪承载力计算公式.与9根超高性能纤维混凝土梁的剪切试验结果进行对比，用推导公式计算的抗剪承载力与试验结果吻合较好，且变异系数较小，可用于有腹筋超高性能纤维混凝土梁的抗剪分析和设计.

超高性能纤维混凝土；腹筋；梁；抗剪承载力；修正压力场理论

超高性能纤维混凝土（ultra-high performance fiber reinforced concrete，UHPFRC）具有超高力学性能和优异的耐久性，工程中利用UHPFRC替代普通混凝土可以缩减结构尺寸、增大跨度、提高耐久性［1－2］.构件抗剪是结构设计中重要一环，然而目前针对UHPFRC梁抗剪性能的研究并不多，主要有：Voo等［3］基于塑性理论提出的无腹筋梁的简化计算模型，该方法假定临界斜裂缝贯穿整个梁高，忽略了剪压区的影响，对20根试验梁计算发现计算结果变异性较大；Graybeal［4］进行了3根预应力无箍筋工字型梁的抗剪试验，通过简化桁架模型反算出剪切破坏时UHPFRC的斜向拉应力比其抗拉强度高38%以上；Hegger等［5］进行了7根预应力工字型无腹筋梁的抗剪试验，7根梁的试验结果平均值比按AASHTO（2010）规范的计算值高出121%；Charles［6］进行了6根复合梁（上部为高性能混凝土面板，下部为UHPFRC工字形梁）的抗剪试验，抗剪承载力试验值比修正压力场理论计算值大19%～59%；陈彬［7］进行了10根预应力超高性能混凝土T梁的抗剪试验并根据国内外几个规范进行了对比计算，表明现有规范不适于UHPFRC梁的抗剪计算.

本文根据UHPFRC梁的剪切破坏机理，考虑上部受压区混凝土对抗剪承载力的贡献，结合修正压力场理论，推导了有腹筋UHPFRC梁抗剪承载力的计算方法.

1 适于UHPFRC梁的修正压力场理论

修正压力场理论是根据钢筋和斜开裂混凝土的平衡条件、变形协调条件及应力－应变关系建立方程，确定受剪截面的荷载－变形反应，并通过迭代的方法对方程求解.考虑UHPFRC材料与普通混凝土的差异，建立纯剪状态下适于UHPFRC的相关方程，见图1.

图1 修正压力场理论

图1（a）为纯剪状态下的钢筋混凝土膜单元，图中v为剪应力，fsx、fsy分别为纵筋应力和箍筋应力，fcx、fcy分别为膜单元纵向和横向应力.图1（b）为混凝土平均应力莫尔圆，根据修正压力场理论，混凝土平均应变满足摩尔协调条件，并假定混凝土的主应力和主应变方向一致，图中f1、f2分别为主拉应力和主压应力，θ为裂缝倾角.图1（c）为裂缝处局部应力，将实际复杂的裂缝理想化成一系列与纵筋呈θ角的平行裂缝，图中vci为裂缝表面剪应力，ftp为跨越裂缝的钢纤维产生的有效拉应力，fsycr、fsxcr分别为裂缝处纵筋应力和箍筋应力.

1.1 应力平衡条件

由图1（a）和（b）可得平衡关系：

式中ρx、ρv为纵筋配筋率和配箍率.

1.2 变形协调条件

式中：εx、εy分别为截面纵向和横向应变，ε1、ε2分别为主拉应变和主压应变，γxy为剪应变.

1.3 裂缝处应力校核

将斜裂缝理想化为相互平行的平面，与纵向钢筋的夹角为θ.与普通混凝土不同，UHPFRC开裂后在裂缝处除了沿裂缝表面的剪应力vci外，尚存在跨越裂缝的钢纤维产生的有效拉应力ftp，由图1（c）有：

由式（7）、（8）可知，跨越裂缝的钢纤维有效拉应力ftp同时减小了横向钢筋和纵筋的应力.

目前未见UHPFRC裂缝表面剪应力vci计算方法的相关研究，可参考普通混凝土公式：

式中a为最大骨料粒径，w为裂缝宽度.

修正压力场理论中，裂缝宽度与假定的裂缝间距有关，裂缝宽度可取为主拉应变ε1与平均斜裂缝间距smθ的乘积，即

根据已有试验［3－8］，UHPFRC梁斜裂缝间距不大于30 mm，可偏保守的取50 mm.

1.4 开裂UHPFRC和钢筋的应力－应变关系

开裂混凝土应力－应变关系的研究需在专有试验仪器上对钢筋混凝土单元施加均匀的膜应力，对开裂UHPFRC应力－应变关系，目前未见相关研究成果.参考普通混凝土应力－应变关系，结合已有研究成果［9－10］，开裂UHPFRC的应力－应变关系采用下式：

式（11）中ε0为UHPFRC峰值压应力对应的应变，取－0.003，ε2为主压应变.

钢筋的应力－应变模型采用理想弹塑性模型：

对以上15个式子联立求解可求得纯剪状态下构件的全过程受力性能.对于同时承受弯矩、剪力和轴力的构件，较精确的算法是进行分层迭代计算，但计算繁杂，不便于设计者使用；目前规范中多以简化的修正压力场理论为基础，通过计算相关参数并查表或直接给出显式计算公式的方法.

2 本文算法

修正压力场理论认为梁的抗剪承载力主要由腹板及箍筋提供，忽略了梁受压区承担的抗剪作用，而实际上，对于承受弯矩、剪力和轴力作用的梁来讲，梁受压区承受较大剪力（尤其是剪跨比较小，受压区高度较大时），若忽略受压区对抗剪的贡献，势必低估梁的抗剪承载力.本文分析UHPFRC梁抗剪承载力时，假定梁截面的剪力由上部受压区混凝土提供的剪力、下部受拉区的骨料咬合力、箍筋承担的剪力、裂缝间钢纤维有效拉应力以及预应力筋预加力对斜截面抗剪承载力的提高作用共同承担，与修正压力场理论一样，忽略纵筋的销栓作用，抗剪模型见图2.

图2 抗剪模型

根据图2，有

式中：Vc为受压区UHPFRC承担的剪力；Vcs为下部受拉区骨料咬合力、箍筋以及钢纤维有效拉应力承担的剪力；Vp为预应力对斜截面承载力的提高值.

2.1 受压区抗剪承载力计算

2.1.1 受压区合力计算

如图2所示，假定受压区任一点处的水平应变为ε，该点到中性轴距离为x，据平截面假定有

式中：ε0为 UHPFRC峰值压应力对应的应变，取0.003；xn为中性轴高度；x0为ε0所对应的截面至中性轴距离；εc为UHPFRC受压边缘应变；εsx为纵筋应变.考虑预应力的影响，忽略受拉区钢纤维有效拉应力的作用，由弯矩、剪力下的平衡条件得到

式中：εx为截面中高度处的纵向应变；M为截面弯矩；V为截面剪力；Vp为预应力对斜截面抗剪承载力提高值；Ap为弯曲受拉侧预应力筋面积；fpo为预应力筋弹性模量与预应力筋和周围混凝土应变差的乘积.为简化计算，可将0.5cotθ偏保守的取为1，分析表明［12］，产生的误差较小，取dv＝0.9d.

梁受压区处于剪压双向受力状态，准确分析应采用UHPFRC的双轴本构关系，但计算会比较复杂，为方便计算受压区提供的剪力，近似按纯弯受力计算受压区合力及中性轴高度，然后考虑剪压破坏准则计算受压区承担的剪力.

根据作者所作UHPFRC单轴抗压试验数据拟合结果，UHPFRC轴压应力－应变关系为

则UHPFRC梁受压区合力为

将式（17）、（19）带入式（20）并整理得：

对于矩形截面：

对于中性轴位于翼缘内的T形截面：

对于中性轴位于腹板内的T形截面：

2.1.2 中性轴高度计算

忽略骨料咬合力的水平分量，由受压区合力与受拉区合力相等，有

将式（21）～（23）分别代入式（24），并考虑平截面假定，整理得中性轴高度.

对于矩形截面：

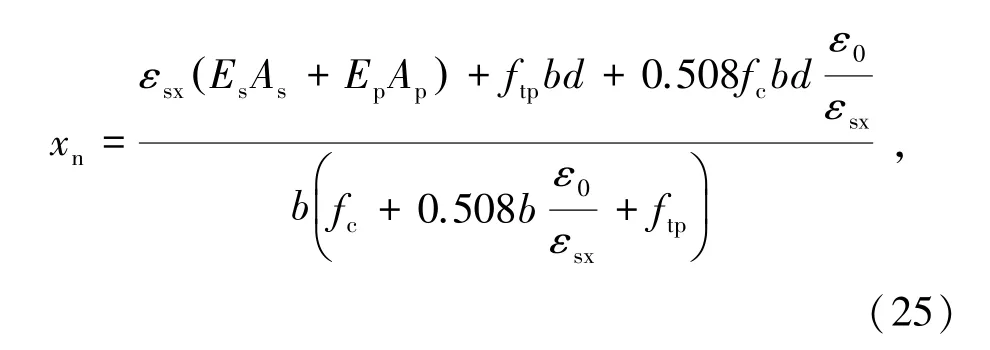
对于中性轴位于翼缘内的T形截面：

对于中性轴位于腹板内的T形截面：

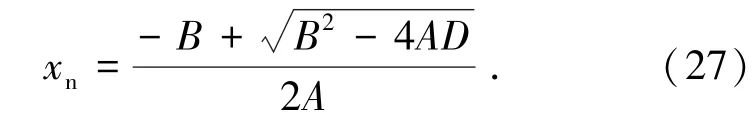
式中

2.1.3 内力臂计算

合力C与受拉钢筋重心的距离为

对式（31）进行计算并整理得：

对于矩形及中性轴位于翼缘内的T形截面：

对于中性轴位于腹板内的T形截面：

2.1.4 受压区抗剪承载力

如图2，受压区同时承受压应力和剪应力的作用，假定极限状态下，混凝土应力满足摩尔应力圆，采用Rankine破坏准则［13］有

式中σ1为主拉应力，f′t为复合应力状态下的抗拉强度.

极限状态下，引入混凝土的抗压强度 fc，式（34）可写为

由于压应力的影响，复合应力状态下的抗拉强度f′t低于单轴抗拉强度ft，对于发生剪切破坏的梁，主压应力并非一个较大的值，因此可简便的取f′t＝ft.根据UHPFRC的基本力学性能试验可知，ft和fc近似呈线性关系，为计算简便，取ft＝0.053fc.根据式（35），可以绘制τ／fc和σc／fc的曲线，见图3，两者近似呈线性关系，对式（35）进行线性化处理，可得剪压区UHPFRC简化破坏准则为

将式（19）代入式（36）可得截面任意点处抗剪强度τ与压应变ε的关系，沿受压区高度进行积分可得受压区提供的抗剪承载力.

式中α1为受压翼缘影响系数，取1.1.

图3 τ／fc和σc／fc关系曲线

2.2 受拉区抗剪承载力计算

正常配箍率情况下，剪切破坏时裂缝处和裂缝间的箍筋均达到屈服强度，则有fsycr＝fv＝fyv，根据修正压力场理论的式（7），受拉区剪应力vcs为

式（38）可表示为

则按修正压力场理论计算的受拉区抗剪承载力可表示为

上式中β和θ的求解，需将修正压力场理论的公式与本文所推导受压区的相关公式结合起来进行迭代求解，不方便为设计者采用.为简化计算，可通过参数分析的方法给出β和θ的显式表达式.考虑到β和θ主要受纵向应变εsx、配箍率ρv以及箍筋强度fyv的影响，因此变换上述参数的取值，利用迭代方法计算相应的β和θ值，然后拟合出β及θ与εsx、ρv、fyv的关系，通过对多种形式表达式的拟合分析，得出β和θ的优化显式表达式：

2.3 计算步骤

根据前面推导的公式对UHPFRC梁进行抗剪承载力计算，计算步骤：

1）假定截面抗剪承载力V0的初始值，根据式（18）计算纵筋应变εsx；

2）由式（25）～（30）计算截面中性轴高度xn；

3）由式（37）计算受压区抗剪承载力Vc；

4）由式（40）～（42）计算受拉区抗剪承载力Vcs；

5）抗剪承载力计算值V＝Vc＋Vcs＋Vp，将计算值与假定的 V0初始值比较，若二者相等（或相差较小），则计算值即为所求抗剪承载力，否则返回第1步，调整V0的初始值，重新计算.

3 试验验证

进行9根T形截面试验梁抗剪试验，T形截面尺寸：高350mm，腹板厚120mm，翼缘宽300 mm、厚50 mm.纵筋及箍筋均采用HRB500钢筋，预应力筋采用公称直径15.2 mm的低松弛1860钢绞线，箍筋采用直径10 mm的HRB500钢筋，实测屈服强度572 MPa；试验采用3 000 kN电液伺服压力试验机进行单点加载.试验梁配筋、实测材料性能及试验结果统计见表 1.λ为剪跨比，s为箍筋间距，ft为UHPFRC轴拉强度，fc为轴压强度，Vu为极限剪力.试验详细过程见文献［8］.

表1 试验梁主要参数及试验结果

根据规范［14－16］、SETRA—AFGC［11］以及本文算法对9根试验梁进行抗剪承载力计算，各梁剪力计算值与试验值的比值见表2.

表2 计算值与试验值比值

裂缝间钢纤维有效拉应力ftp的值主要受钢纤维类型、钢纤维掺量、钢纤维与基体粘结强度、裂缝宽度等因素的影响，本文计算时采用文献［3］的计算模型，计算公式为

式中：αf为钢纤维长径比，ρf为钢纤维体积掺量，τb为钢纤维与基体粘结强度.

预应力对斜截面承载力的提高值Vp目前尚无准确算法，本文计算时参考GB 50 010—2 010《混凝土结构设计规范》［15］，取

由表2知，与试验值相比，依据4个规范所得计算值均过于保守，SETRA—AFGC为法国土木工程协会制定的UHPFRC设计建议，相比前三个规范，其计算结果较接近试验值，但依然偏于保守.本文算法中除试件L3和L7外，其余试件计算值与试验值吻合良好.分析试件L3和L7计算值偏小的原因，在于这两个试件剪跨比较小（1.03和1.73），L3破坏形式为斜压破坏，L7破坏形式介于斜压和剪切破坏之间，本文计算模型没有考虑小剪跨比时支座和加载点之间拱作用的有利影响，从而低估了剪跨比较小的梁的抗剪承载力.从表2还可看到，相比未施加预应力的试件，本文算法中预应力试件计算值偏小，这与计算中所取预应力对斜截面承载力的提高值Vp偏保守有一定关系.除去剪跨比较小的试件L3和L7，5种算法中其余7根发生剪压破坏的试验梁的抗剪承载力计算值与试验值比值的平均值依次为0.39、0.39、0.54、0.80和0.96，变异系数依次为0.11、0.15、0.09、0.16和0.11，可见本文算法不仅与试验结果吻合较好，且变异系数不大.

为进一步验证本文方法的适用性，利用本文方法对文献［7］中的6根发生剪切破坏的有腹筋试验梁进行了计算，计算结果见表3，Vt为试验值，Vc为计算值.

表3 文献［7］计算值与试验值对比

4 结 语

根据UHPFRC梁的剪切破坏机理，考虑上部受压区和下部受拉区共同承担剪力，上部受压区采用简化的双轴应力准则得到混凝土抗剪承载力，下部受拉区采用简化的修正压力场计算公式得到抗剪承载力，得出了有腹筋UHPFRC梁抗剪承载力的显式计算公式.计算表明，本文公式适用于发生剪压破坏的有腹筋UHPFRC梁的抗剪承载力的计算.

［1］徐海宾，邓宗才.超高性能混凝土在桥梁工程中的应用［J］.世界桥梁，2012，40（3）：63－67.

［2］STEINBERG E.Structure reliability of prestressed UHPC flexure models for bridge girders［J］.Journal of Bridge Engineering，ASCE，2010，15（1）：65－72.

［3］VOO Y L，POONW K，FORSTER S J.Shear strength of steel fiber-reinforced ultrahigh-performance concrete beams without stirrups［J］.Journal of Structural Engineering，2010，136（11）：1393－1399.

［4］GRAYBEAL B.Characterization of the behavior of ultrahigh performance concrete［D］.Maryland：University of Maryland，2005.

［5］HEGGER J，BERTRAMG.Shear carrying capacity of steel fiber reinforced UHPC［C］／／2nd International Symposium on Ultra High Performance Concrete.Germany，Kassel：Kassel University Press，2008：513－520.

［6］CHARLESK C.Shear and shear friction of ultra-high performance concrete brdige girders［D］.Atlanta：Georgia Institute of Technology，2010.

［7］陈彬.预应力RPC梁抗剪性能研究［D］.长沙：湖南大学，2007.

［8］徐海宾，邓宗才，陈春生，等.超高性能纤维混凝土梁抗剪性能试验研究［J］.土木工程学报，2014，47（12）：91－97.

［9］VECCHIO F J，COLLINSM P.Themodified compression field theory for reinforced concrete elements subjected to shear［J］.ACIStructure Journal，1986，83（2）：219－231.

［10］TAN K H，MURUGAPPAN K.Shear behavior of steel fiber reinforced concrete beams［J］.ACIStructure Journal，1993，90（1）：3－11.

［11］AFGC.Ultra high performance fibre-reinforced concretes，interim recommendations［M］.France：AFGC Publication，2002.

［12］BENTZ E C，COLLINS M P.Development of the 2004 Canadian Standard Association（CSA） A23.3 shear provisions for reinforced concrete［J］.Canadian Journal of Civil Engineering，2006（33）：521－534.

［13］CHEN W F.Plasticity in reinforced concrete［M］.New York：McGraw-Hill，1982.

［14］JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［15］GB50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［16］CECS38：2004纤维混凝土结构技术规程［S］.北京：中国计划出版社，2004.

（编辑赵丽莹）

Shear capacity of UHPFRC beam s w ith stirrups

XU Haibin1，2，DENG Zongcai1

（1.Beijing Key Lab of Earthquake Engineering and Structural Retrofit（Beijing University of Technology），100124 Beijing，China；2.School of Civil Engineering，Henan Polytechnic University，454003 Jiaozuo，Henan，China）

The equation for the shear capacity of UHPFRC beams with stirrups is deduced to study the shear capacity of UHPFRC beams with stirrups，based on the modified compression field theory，and considering the shear contribution of concrete in compression，shear stress transmitted across crack interface，shear carried by steel fibers and stirrups.The analysis results of nine tested UHPFRC beams in shear by the proposed equation agreewell with the test values，and the variation coefficient is small.It is suitable for shear analysis and design for UHPFRC beamswith stirrups.

ultra-high performance fiber reinforced concrete；stirrup；beam；shear capacity；modified compression field theory

TU375.1

A

0367－6234（2015）12－0080－06

10.11918／j.issn.0367-6234.2015.12.014

2015－01－04.

国家自然科学基金（51378032）；北京市自然科学基金（8142005）；河南理工大学青年基金（Q2014－08A）.

徐海宾（1979—），男，博士，讲师；邓宗才（1961—），男，教授，博士生导师.

邓宗才，dengzc＠bjut.edu.cn.